武器装备研制是一个庞大而复杂的系统工程,包括从立项到定型研制的全过程,由于其规模大、周期长、技术新等特点,导致了武器装备的研制过程充满了不确定性和风险性[1].目前,国内外关于武器装备研制项目风险的研究也较多,Mavris等[2]提出了一种技术识别评估与选择法(technology identification,evaluation,and selection,TIES),应用于航天器设计的技术不确定性预测中,但该方法只能从定性角度评估,无法得到定量结果;Fox等[3]提出一种聚簇分析技术应用在航天项目费用风险评估,该方法定向性强,不能同时考虑风险的多元性;Sun等[4]提出了一种基于模糊集理论评估武器装备项目风险的方法,该方法可以弥补装备研制过程中的不确定性,但在相应权向量的确定中,通常采用AHP等方法,带有明显的主观性,另外由于风险级别评语本身的模糊性,求解隶属函数也比较复杂.因此,本文将云模型引入模糊算法中解决该问题.云模型[5]是在传统模糊集理论和概率统计的基础上提出的,以一个以自然语言值为切入点,实现定性概念与定量数值之间的不确定性转换模型,它最大的优势是把定性概念的模糊性和随机性完全集成在一起,构成定性、定量相互间的映射.在武器装备研制项目风险评估程中,利用云模型的优势改进传统模糊综合评判法中的综合评判矩阵和权重矩阵,从而确定评价对象的风险等级,最大程度的克服直接赋值的主观性,并以云滴形式展现出来,更加直观,因此,本文认为利用云模型和模糊判别理论进行武器装备研制项目风险传导评估是可行的.
1 二维正态云模型在介绍云模型前,首先引入云的概念[6]:设U是一个用精确数值表示的定量论域,C是U上的定性概念,若定量值x∈U,且x是定性概念C的一次随机实现,x对C的确定度μ(x)∈[0,1]是具有稳定倾向的随机数.若
| $\mu :U\to [0,~1],\forall x\in U,x\to \mu \left( x \right),$ |
则x在论域U上的分布称为云,每一个x称为一个云滴.
正态云模型是最基本的云模型.云的数字特征用期望Ex(expected value)、熵En(entropy)、超熵He(hyper entropy)来表示[7].通过研究正态模型的分布函数,本文可以掌握随机变量的统计规律,下面给出正态分布的函数:
| $F(x,\mu ,{{\sigma }^{2}})=\frac{1}{\sqrt{2\pi }\sigma }\int_{-\infty }^{x}{exp}[-\frac{{{\left( u-\mu \right)}^{2}}}{2{{\sigma }^{2}}}]du.$ |
其概率密度函数为
| $f(x,\mu ,{{\sigma }^{2}})=\frac{1}{\sqrt{2\pi }\sigma }exp[-\frac{{{\left( u-\mu \right)}^{2}}}{2{{\sigma }^{2}}}].$ |
根据统计学理论,正态分布的期望和方差是相互影响的.但在云发生器构成过程中,把熵En看成是与期望Ex独立的另一个数字特征,同时考虑到正态分布的普适性,又把熵En作为超熵He的期望,用正态分布产生随机熵En'.再用随机熵En'作为期望Ex的熵,生成不确定性概念的一次正态分布的随机精确量值.刘金保等[8]提出了一维正态云的生成算法,但是,在现实世界中,很多概念并不是从某一单个意义上来阐述,而是和许多因素有着千丝万缕的关系.将一维云模型扩展至二维甚至多维,使其可以定性的去描述武器装备研制的风险发生的概率以及风险后果的影响程度,因此,在一维云算法的基础上,提出二维正态云算法.
设二维论域的两维之间互不相关,二维正态云可以用6个数字特征量来描述:(Ex,Enx,Hex,Ey,Eny,Hey).其中:Ex、Ey分别为期望值;Enx、Eny分别为熵; Hex、Hey分别为超熵.二维云可描述为一个在(X,Y,μ)中的三维图形,(Ex,Ey)是二维云在XOY平面上投影面积的形心,反映了相应的两个定性概念组合而成的定性概念的信息中心值;(Enx,Eny)是二维云在XOμ平面和YOμ平面上投影期望曲线的熵,反映了该语言值对二维数值的可覆盖程度;(Hex,Hey)是二维云在XOμ平面和YOμ平面上投影的厚度,反映了云滴的离散程度.
二维正态云的生成算法如下.
Step 1 根据由(xi,yi)→z(xi,yi)的推理规则,给出关于z(xi,yi)的j个评语集.
Step 2 对每一条单规则,生成以(Ex,Ey)为期望值,(Enx,Eny)为标准差的二维正态随机数(Exj,Eyj).
Step 3 生成以(Exj,Eyj)为期望值,(Hex,Hey)为方差的正态随机数(Exj',Eyj').
Step 4 计算
Step 5 重复Step 2~4,直到产生n个云滴为止.
2 基于正态云模型的风险传导单一影响因子评估运用云模型对武器装备研制项目风险传导进行评估的内容分为两部分:首先采用云模型和模糊评判理论,计算单一风险传导影响因子对进度、费用和性能风险产生的影响大小;然后运用加权求和的方式,计算所有风险传导影响因子对进度、费用和性能风险产生的影响大小.
2.1 评估流程武器装备研制项目传导的每一个影响因子都会对武器装备的进度、费用和性能产生影响,因此首先要对单一风险影响因子对每一类风险的影响大小进行评估,然后综合考虑对3类风险的影响,得到单一影响因子对项目风险的总影响值.基于云模型的风险传导单一影响因子评估流程,如图 1所示.

|
图 1 基于云模型的风险传导单一影响因子评估流程 Figure 1 The flow of evaluating single impact factor in the risk transmission based on the cloud model |
在武器装备研制项目风险传导过程中,每一个影响因子都可能对项目的进度、费用和性能产生影响.本文假设项目风险传导的各级影响因子是相互独立的,对每一个影响因子产生的进度、费用和性能风险影响分别进行评估,是武器装备研制项目风险传导综合评估的基础.
2.2 变量云化单一风险传导影响因子对武器装备研制项目进度、费用和性能风险的影响包括3个定性变量即影响因子对风险产生影响的概率、影响程度和影响大小,通常是采用专家打分法进行赋值.所以,本文采用变量云化对定性的变量进行云描述,从而获取云数字特征(Ex,En,He)和云的形状.
影响因子对项目进度、费用和性能风险的影响大小的定性描述评语集分为9个等级:非常低、很低、较低、低、中等、高、较高、很高、非常高.
通过专家咨询得到单一风险传导影响因子对风险产生影响概率、影响程度和影响大小的云数字特征(Ex,En,He).
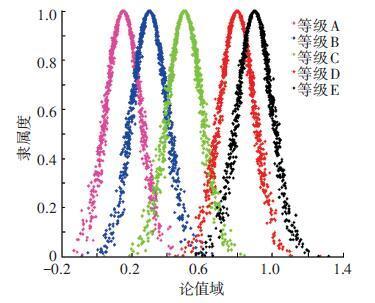
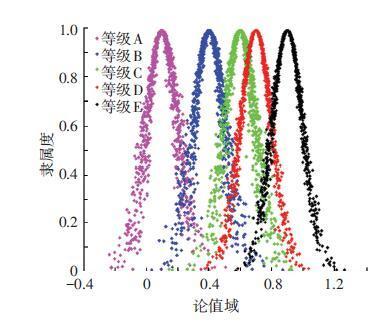
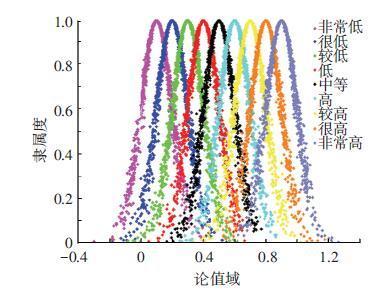
2.3 构造云标尺在MATLAB环境下,根据得到云数字特征,按照一维正态云算法步骤[8],进行1 000仿真试验,将云化后的定性变量结果排列在坐标尺上,构成云标尺.云标尺中的云簇即为定性变量的激活区间,如图 2~8所示.

|
图 2 影响因子产生进度风险影响概率云标尺 Figure 2 The cloud scale plate based on the incidence probability played on schedule risk by impact factor |
|
图 3 影响因子产生费用风险影响概率云标尺 Figure 3 The cloud scale plate based on the incidence probability played on cost risk by impact factor |

|
图 4 影响因子产生性能风险影响概率云标尺 Figure 4 The cloud scale plate based on the incidence probability played on performance risk by impact factor |

|
图 5 影响因子对进度风险影响程度云标尺 Figure 5 The cloud scale plate based on the incidence played on schedule risk by impact factor |
|
图 6 影响因子对费用风险影响程度云标尺 Figure 6 The cloud scale plate based on the incidence played on cost risk by impact factor |

|
图 7 影响因子对性能风险影响程度云标尺 Figure 7 The cloud scale plate based on the incidence played on performance risk by impact factor |
|
图 8 影响因子对风险影响大小云标尺 Figure 8 The cloud scale plate based on the incidence played on the risk by impact factor |
由各种云发生器组合起来构造的定性规则能够实现从一个定性概念到另一个定性概念的推理.根据风险传导影响因子发生概率、影响程度和影响大小之间的关系,可以构造多个二维云单规则生成器,如“IF A and B,THEN C”,多个二维云单规则生成器组在一起就构成了二维多规则生成器.
构造风险传导影响因子发生概率、影响程度和影响大小之间的定性规则,见表 1.
| 表 1 风险传导定性评估规则 Table 1 The qualitative evaluation regulation of risk conduction |
结合上述规则,生成如图 9所示的多规则生成系统,实现定性分析向定量分析的云转换,图中A表示影响因子发生的概率,B表示影响程度,C表示对风险的影响大小.

|
图 9 云发生器 Figure 9 The cloud generator |
构造云发生器后,任一风险传导影响因子的相关信息都可以通过云发生器,输出该影响因子对风险影响的大小,具体算法如下.
Step 1 对每一个单规则,令(EnAi,EnBi)为期望、(HeAi,HeBi)为方差,生成符合二维正态分布的一个二维随机值(EnAij,EnBij),其中i=1,2;j=1,2,…,14.
Step 2 令xA为影响因子发生概率的输入值,xB为影响程度的输入值,EC表示对风险影响大小的输出值.通过已知的影响因子输入值C(xa,xb),可以得到每一个单规则生成器的激活强度,即隶属度μij为
| ${{\mu }_{ij}}=exp-[\frac{{{({{x}_{a}}{{E}_{x{{A}_{i}}}})}^{2}}}{2E_{n{{A}_{ij}}}^{2}}+\frac{{{({{x}_{b}}-{{E}_{x{{B}_{i}}}})}^{2}}}{2E_{n{{B}_{ij}}}^{2}}].$ |
Step 3 取μij中最大值μj1和次大值μj2,激活其对应的两条单规则,通过这两条单规则给定后的(Enck,Hck),随机生成以Enck为期望,Hck为方差的一维正态随机值Enck1、Enck2,k∈[1,14].
Step 4 根据下式求得μj1、Enck1条件下的两个yc1值和μj2、Enck2条件下的两个yc2值.
| $\begin{align} & ~{{\mu }_{j1}}=exp\frac{{{\left( {{y}_{{{c}_{1}}}}-{{E}_{xc{{k}_{1}}}} \right)}^{2}}}{2E_{nc{{k}_{1}}}^{2}}, \\ & {{\mu }_{j2}}=exp\frac{{{({{y}_{{{c}_{2}}}}-{{E}_{xc{{k}_{2}}}})}^{2}}}{2E_{nc{{k}_{2}}}^{2}}. \\ \end{align}$ |
Step 5 各取两个yc1和yc2中的一个,使之距离较另外的yc1和yc2的距离要小,得到两个云滴(yc1,μj1)和(yc2,μj2).输出值可由下式求得:
| ${{E}_{xc}}=\frac{{{y}_{{{c}_{1}}}}\sqrt{-2\ln ({{\mu }_{j2}})}+{{y}_{{{c}_{2}}}}\sqrt{-2\ln ({{\mu }_{j1}})}}{\sqrt{-2\ln ({{\mu }_{j1}})}+\sqrt{-2\ln ({{\mu }_{j2}})}}.$ |
为使得到的结果更加科学,本文将运用仿真方法进行计算,通过多次重复上述计算步骤,取所有云滴点坐标的平均值作为结果输出,这个定量结果就是该类影响因子对风险影响的大小.
3 风险传导综合评估根据以上计算,可以得到武器装备研制项目单一影响因子对进度、费用和性能风险大小的影响,分别用Rsi,Rci,Rfi表示,i∈[1,14].每一个影响因子在进度、费用和性能3个方面彼此独立的产生不同的影响,因此在对单一类型风险传导进行评估时,要根据每一个影响因子的特点赋予不同的权重,即wi=(wsi,wci,wfi),i∈[1,14],∑wsi=∑wci=∑wfi=1,最后用加权求和的方法进行综合评估.
| ${{R}_{s}}=\sum {{w}_{si}}{{R}_{si}},{{R}_{c}}=\sum {{w}_{ci}}{{R}_{ci}},{{R}_{p}}=\sum {{w}_{fi}}{{R}_{fi}}.$ | (1) |
各目标权重系数的确定,是线性加权求解的关键.一般来说,本文采用主观和客观法来确定权重[9].在武器装备研制项目中,影响因子对风险产生的影响是未知的,难以得到客观数据.同时每个项目都是非重复性的,无法照搬以往项目的经验.因此,按照模糊理论对主观赋权值进行处理是简便可行的方法.那么如何将各个权重系数进行归一化处理,使其具有可加性,是本文研究的另一个重点.
依据夏喆等[10]对风险传导影响因子的分析,建立了风险传导评估指标的结构层次体系.权重的确定过程中,需要对比每个影响因子,并构造判断矩阵.其中,互补判断矩阵是一类常用的判断矩阵形式.由于判断是不确定的,因此,在构造互补判断矩阵时,判断值有时是以三角模糊数形式给出的[11].
这里假设a=(al,am,au),其中,0<al<am<au,称a
| $~{{\mu }_{a}}\left( x \right)=\left\{ \begin{align} & \frac{x-{{a}_{l}}}{{{a}_{m}}-{{a}_{l}}},{{a}_{l}}\le x\le {{a}_{m}}; \\ & \frac{x-{{a}_{u}}}{{{a}_{m}}-{{a}_{u}}},{{a}_{m}}\le x\le {{a}_{u}}; \\ & 0,其他. \\ \end{align} \right.$ |
设a=(al,am,au),b=(bl,bm,bu),下面给出两种关于三角模糊数的运算:
| $\begin{align} & \frac{1}{a}=\left( \frac{1}{{{a}_{u}}},\frac{1}{{{a}_{m}}},\frac{1}{{{a}_{l}}} \right), \\ & a+b=({{a}_{l}},{{a}_{m}},{{a}_{u}})+({{b}_{l}},{{b}_{m}},{{b}_{u}})= \\ & ({{a}_{l}}+{{b}_{l}},{{a}_{m}}+{{b}_{m}},{{a}_{u}}+{{b}_{u}}). \\ \end{align}$ |
令N={1,2,…,n},设判断矩阵A=(aij)n×n,若aij+aij=1,aij>0,i,j∈N,则称矩阵A是互补判断矩阵.
设判断矩阵A=(aij)n×n,其中,aij=(alij,amij,auij),aji=(alji,amji,auji),若alij+auji=amij+amji=auij+alji,alij≥amij≥auij≥0,i,j∈N,则称矩阵A是三角模糊数互补判断矩阵.
设a=(al,am,au),b=(bl,bm,bu),则a≥b的可能度为[12]
| $\begin{align} & ~P\left( a\ge b \right)=\lambda \max \left\{ 1-\max \left( \frac{{{b}_{m}}-{{a}_{l}}}{{{a}_{m}}-{{a}_{l}}+{{b}_{m}}-{{b}_{l}}},0 \right),0 \right\}\text{ }+ \\ & \left( 1-\lambda \right)\max \left\{ 1-\max \left( \frac{{{b}_{u}}-{{a}_{m}}}{{{a}_{u}}-{{a}_{m}}+{{b}_{u}}-{{b}_{m}}},0 \right),0 \right\} \\ \end{align}$ | (2) |
其中λ∈[0,1].
λ的值取决于决策者的态度:当λ>0.5时,决策者态度是积极的;当λ=0.5时,决策者态度是中立的;当λ<0.5时,决策者态度是消极的.特别地,当λ=1时,称p(a≥b)为a≥b的悲观可能度;当λ=0时,称p(a≥b))为a≥b的乐观可能度[13].
在参考可能度概念的基础上,得到三角模糊数互补判断矩阵的排序规则,具体步骤如下.
Step 1 设有n个影响因子x1,x2,…,xn,专家对n个因素进行相互比较,得到三角模糊数互补判断矩阵A=(aij)n×n,其中aij=(alij,amij,auij)是三角模糊数.当因素xi和因素xj进行相互比较时,其 xi相对于xj重要度的最保守估计、最可能估计和最乐观估计分别为记为alij,amij,auij.
Step 2 计算三角模糊数互补判断矩阵A的行和,并进行归一化,得到三角模糊数权重向量w=(w1,w2,…,wn)T,其中
| $\begin{align} & {{w}_{i}}=\frac{\sum\limits_{j=1}^{n}{{{a}_{ij}}}}{\sum\limits_{i=1}^{n}{\sum\limits_{j=1}^{n}{{{a}_{ij}}}}}=\frac{\sum\limits_{j=1}^{n}{({{a}_{lij}},{{a}_{mij}},{{a}_{uij}})}}{\sum\limits_{i=1}^{n}{\sum\limits_{j=1}^{n}{\left( {{a}_{lij}},{{a}_{mij}},{{a}_{uij}} \right)}}}= \\ & \frac{\left( \sum\limits_{j=1}^{n}{{{a}_{lij}}},\sum\limits_{j=1}^{n}{{{a}_{mij}}},\sum\limits_{j=1}^{n}{{{a}_{uij}}} \right)}{\left( \sum\limits_{i=1}^{n}{\sum\limits_{j=1}^{n}{{{a}_{lij}}},\sum\limits_{i=1}^{n}{\sum\limits_{j=1}^{n}{{{a}_{mij}}},\sum\limits_{i=1}^{n}{\sum\limits_{j=1}^{n}{{{a}_{uij}}}}}} \right)}= \\ & \frac{\sum\limits_{j=1}^{n}{{{a}_{lij}}}}{\sum\limits_{i=1}^{n}{\sum\limits_{j=1}^{n}{{{a}_{uij}}}}},\frac{\sum\limits_{j=1}^{n}{{{a}_{mij}}}}{\sum\limits_{i=1}^{n}{\sum\limits_{j=1}^{n}{{{a}_{mij}}}}},\frac{\sum\limits_{j=1}^{n}{{{a}_{uij}}}}{\sum\limits_{i=1}^{n}{\sum\limits_{j=1}^{n}{{{a}_{lij}}}}}, \\ & (i,j\in N.) \\ \end{align}$ | (3) |
Step 3 把三角模糊数wi(i∈N)进行两两相互比较,并利用式(2)计算相应的可能度P(wi≥wj),记为pij,i,j∈N,得出可能度矩阵P=(pij)n×n.
Step 4 矩阵P包括两两相互比较的可能度信息,因此,三角模糊数的排序可以转化成求解可能度矩阵的排序向量,参考文献[14-15],给出排序公式如下:
| ${{w}_{i}}=\frac{1}{n}\left( \sum\limits_{j=1}^{n}{{{p}_{ij}}}+1-\frac{n}{2} \right),\left( i\in N. \right)$ | (4) |
求解得到可能度矩阵P的排序向量,即各影响因子的权重W=(w1,w2,…,wn).
4 案例分析本文以高超音速巡航导弹X-51项目为例对风险传导的识别与评估进行分析,初始数据的采集来源于某大学和某科研院所在火箭推进系统方面研究多年的知名教授和研究员.为便于研究,选取承担发动机研制任务的惠普(HP)公司为对象,分析在发动机的工程研制阶段该公司的风险传导问题.以该公司为核心企业,构建SJX61-2发动机项目的风险在相关企业之间的传导结构,如图 10所示.

|
图 10 SJX61-2发动机项目的风险传导结构 Figure 10 The risk conduction structure of SJX61-2 engine |
根据专家问卷调查的统计结果,得到工程研制阶段HP公司风险影响因子对项目进度、费用和性能风险产生影响的概率和影响程度的输入值,见表 2.
| 表 2 影响因子对进度、费用和性能风险的影响概率和影响程度输入 Table 2 The input values of the incidence and incidence probability played on schedule,cost and performance risk by impact factor |
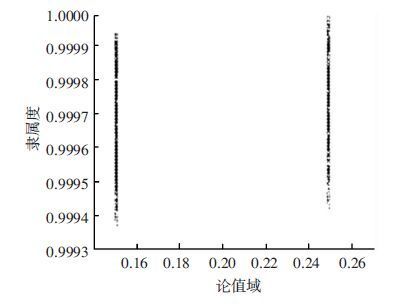
以“风险缓冲计划”这一影响因子为例,按照文中给出的云模型算法进行仿真计算.将影响概率输入值xa=0.12和影响程度输入值xb=0.24输入模型,进行1 000次仿真,得到若干个(yC1,μj1)和(yC2,μj2)云滴,如图 11所示.图 11中云滴相对集中在两个部分,计算所有云滴横坐标的平均值,得到风险缓冲计划对风险影响大小Rji=0.2.
|
图 11 单一影响因子对风险影响大小仿真结果 Figure 11 The simulation of the incidence played on the risk by single impact factor |
同理可以得到其他风险传导影响因子对进度、费用和性能风险影响的数值,见表 3,其中得到风险传导影响因子对进度风险的总影响值为7.79,小于风险传导识别时计算得到的影响值8.84,证明了风险传导识别所用的计算方法是可行的.
| 表 3 单一影响因子对进度、费用和性能风险影响值 Table 3 The incidence played on schedule,cost and performance risk by single impact factor |
从表 3中可见,信息渠道、运转效率、控制措施、配套协调、人员能力是影响进度风险的高风险影响因子;缓冲计划、配套协调是影响费用风险的高风险影响因子;控制措施是影响性能风险的高风险影响因子.对表 3中的结果进行加权处理,根据影响因子对进度、费用和性能风险的重要程度,运用三角模糊数确定相应权重,用式(1)和式(3)计算出单一影响因子对总风险的影响大小并进行排序,从而判断该阶段何种影响因子最值得关注,计算结果见表 4.
| 表 4 风险传导影响因子对总风险的影响值 Table 4 The incidence played on the total risk by risk conduction impact factor |
从表 4中容易看出对进度风险影响较大的影响因子主要是信息渠道、运转效率、控制措施、配套协调与人员能力,而对整体风险影响较大的主要是控制措施和配套协调,这些就是风险管理需要加强监控和管理的指标.
5 结 论1) 从分析中可以看出,武器装备的研制首先离不开技术实力的支持,技术风险仍然是风险的主要来源.本文针对风险传导效应的量化评估问题,提出了一种二维正态云模型的评估算法,从计算单一风险传导影响因子对进度、费用和性能风险产生的影响大小入手,再通过加权求和法,计算所有风险传导影响因子产生的总影响.
2) 在可能度理论的基础上,给出三角模糊数互补判断矩阵的排序方法,得到综合风险值.最后以承担X-51项目发动机研制任务的HP公司为对象,分析验证了算法的可行性,为风险传导的管理者提供决策参考.
| [1] |
SUN Jiangsheng, ZHAO Fanggeng, LV Yanmei, et al. Research on three-echelon inventory model and algorithm for valuable spare parts in weapon equipment[J].
Journal of China Ordnance,2012, 8 (1) : 52-58.
DOI: 10.3969/j.issn.1672-002X.2012.01.010 ( 0) 0)
|
| [2] |
MAVRIS D N, KIRBY M R. Technology identification, evaluation, and selection for commercial transport aircraft[C]//For Presentation at the 58th Annual Conference. San Jose, California: Society of Allied Weight Engineers, Inc., 1999. https://smartech.gatech.edu/bitstream/handle/1853/6392/SAWE-99-2456.pdf sequence=1.
( 0) 0)
|
| [3] |
FOX G, EBBELER D H, JORGENSEN E J. The use of cluster analysis techniques in spaceflight project cost risk estimation[C]//AIAA Space 2003 Conference & Exposition, SPACE Conferences and Exposition. Longbeach, CA: AIAA, 2003-6298. DOI: 10.2514/6.2003-6298.
( 0) 0)
|
| [4] |
SUN Jiangsheng, HUANG Rufu, CHEN Dailin, et al. Fuzzy set-based risk evaluation model for real estate projects[J].
Tsinghua Science and Technolngy,2008, 13 (S1) : 158-164.
DOI: 10.1016/S1007-0214(08)70143-3 ( 0) 0)
|
| [5] |
阎长顺, 李一军. 基于云模型的动态客户细分分类模型研究[J].
哈尔滨工业大学学报,2007, 39 (2) : 299-302.
DOI: 10.3321/j.issn:0367-6234.2007.02.033 YAN Changshun, LI Yijun. Analysis of dynamic consumer detailed segmentation model based on cloud model[J]. Journal of Harbin Institute of Technology,2007, 39 (2) : 299-302. DOI: 10.3321/j.issn:0367-6234.2007.02.033 (  0) 0)
|
| [6] |
YANG Bin, ZHU Zhongying. Mining multilevel spatial association rules with cloud models[J].
Journal of Harbin Institute of Technology,2005, 12 (3) : 314-318.
( 0) 0)
|
| [7] |
LI Deyi, HAN Jiawei, SHI Xuemei, et al. Knowledge representation and discovery based on linguistic atoms[J].
Knowledge-based System,1998, 10 (7) : 431-440.
DOI: 10.1016/S0950-7051(98)00038-0 ( 0) 0)
|
| [8] |
刘金保, 王智琳, 李政. 基于PLC的一维正态云模型实现研究[J].
电子设计工程,2012, 20 (1) : 158-160.
DOI: 10.3969/j.issn.1674-6236.2012.01.059 LIU Jinbao, WANG Zhilin, LI Zheng. Realization of one-dimensional normal cloud mode on PLC[J]. Electronic Design Engineering,2012, 20 (1) : 158-160. DOI: 10.3969/j.issn.1674-6236.2012.01.059 (  0) 0)
|
| [9] |
谢学铭, 郑健. 基于云模型主观赋权法的多目标决策研究[J].
中国西部科技,2009, 8 (25) : 7-8.
DOI: 10.3969/j.issn.1671-6396.2009.25.004 XIE Xueming, ZHENG Jian. To study on multi-objective decision-making based on cloud model subjective weight determination[J]. Science and Technology of West China,2009, 8 (25) : 7-8. DOI: 10.3969/j.issn.1671-6396.2009.25.004 (  0) 0)
|
| [10] |
夏喆, 邓明然. 企业风险传导过程中的规律研究[J].
当代经济管理,2006, 28 (5) : 32-35.
DOI: 10.3969/j.issn.1673-0461.2006.05.006 XIA Zhe, DENG Mingran. A study on rules of enterprise risk conduction[J]. Contemporary Economy & Management,2006, 28 (5) : 32-35. DOI: 10.3969/j.issn.1673-0461.2006.05.006 (  0) 0)
|
| [11] |
刘仁辉, 张劲强, 韩喜双. 三角模糊数的工程项目风险识别[J].
哈尔滨工业大学学报,2008, 40 (10) : 1617-1620.
DOI: 10.3321/j.issn:0367-6234.2008.10.023 LIU Renhui, ZHANG Jingqiang, HAN Xishuang. Risk identifiation based on triangular fuzzy number for construction project[J]. Journal of Harbin Institute of Technology,2008, 40 (10) : 1617-1620. DOI: 10.3321/j.issn:0367-6234.2008.10.023 (  0) 0)
|
| [12] |
钱伟懿, 曾智. 基于可能度的区间粗糙数排序方法[J].
运筹与管理,2013, 22 (1) : 71-76.
DOI: 10.3969/j.issn.1007-3221.2013.01.012 QIAN Weiyi, ZENG Zhi. Method for ranking interval rough numbers based on possibility degree[J]. Operations Research and Management Science,2013, 22 (1) : 71-76. DOI: 10.3969/j.issn.1007-3221.2013.01.012 (  0) 0)
|
| [13] |
高峰记. 可能度及区间数综合排序[J].
系统工程理论与实践,2013, 33 (8) : 2033-2040.
DOI: 10.3969/j.issn.1000-6788.2013.08.017 GAO Fengji. Possibility degree and comprehensive priority of interval numbers[J]. Systems Engineering—Theory & Practice,2013, 33 (8) : 2033-2040. DOI: 10.3969/j.issn.1000-6788.2013.08.017 (  0) 0)
|
| [14] |
LI W L, CHEN C Y, CHEN C W, et al. Application of half-circle fuzzy numbers and development of triangular fuzzy numbers to fuzzy control[C]//Proceedings of the 10th WSEAS International Conference on Applied Computer Science. Stevens Point. Wisconsin:World Scientific and Engineering Academy and Society,2010: 335-340.
( 0) 0)
|
| [15] |
周佳敏, 王展青. 基于三角模糊数的动态混合多属性决策方法[J].
武汉理工大学学报(信息与管理工程版),2014, 36 (1) : 121-124.
DOI: 10.3963/j.issn.2095-3852.2014.01.028 ZHOU Jiamin, WANG Zhanqing. Method of dynamic hybrid multi-attribute decision based on triangular fuzzy numbers[J]. Journal of Wuhan University of Technology (Information & Management Engineering),2014, 36 (1) : 121-124. DOI: 10.3963/j.issn.2095-3852.2014.01.028 (  0) 0)
|
 2016, Vol. 48
2016, Vol. 48


