空间展开机构地面展开试验是卫星研制阶段重要考核内容.为确保卫星型号在轨任务的成功执行,空间展开机构需要在地面进行充分的展开试验以验证其展开性能、展开可靠性,并对展开试验的准确性进行评估.空间展开机构地面展开试验的主要目的是:考核结构和机构的协调性以及展开功能的可靠性、稳定性;检验结构与机构部分各项指标与总体技术要求的符合性.马兴瑞等[1]对空间飞行器机构的分类与构成,对展开与驱动机构的国内外研究概况进行了分析.从强[2]总结归纳了空间机构地面重力补偿的方法,提出了地面重力补偿的影响分析及设计原则.任守志等[3]建立了太阳翼与展开试验装置的联合分析模型,分析了影响展开试验的主要因素.
卫星太阳翼一般采用刚性或半刚性基板,通过铰链和绳索同步机构(CCL)组装在一起的多体结构.在总装与展开测试时,通常将太阳翼板面垂直于地面放置,采用竖直悬挂或气浮支撑方式开展太阳翼展开试验.两种展开试验方式主要有以下共同点:1)均采取板面垂直于地面放置方式,其铰链驱动力矩与重力场相互正交,实现了铰链驱动力与吊挂力(气浮力)、重力的解耦;2)展开过程中影响因素主要有空气阻力、悬挂或气浮系统的摩擦阻力等.目前,两种方式已广泛应用了太阳翼、磁强计、天线、机械臂等空间机构地面展开试验中[4-10].但是,对于某些大型光学卫星,若太阳翼展开试验沿用传统竖直悬挂或气浮支撑方式,则卫星姿态需要侧转90°,光学相机处于长时间侧卧状态,引起相机间的相对指向精度发生1'的角度变化,超过相机间的相对指向精度要求,而光学相机精度保证是研制阶段最重要的质量考核项目,故需要开展新型展开方法研究,确保大型光学相机精度要求.本文提出了一种卫星太阳翼板面水平展开试验方法,解决了卫星太阳翼水平装配、水平展开、水平测试等难题,重点对水平展开试验方法进行了运动学及动力学仿真分析与试验验证,试验结果表明,该方法能够更真实的模拟太阳翼在轨展开运动,满足卫星太阳翼展开试验要求.该方法已直接应用于某型号卫星太阳翼展开试验,可推广应用于磁强计、天线、空间机械臂等空间展开机构地面展开试验.
1 试验方法为满足太阳翼多维展开运动及平衡重力的要求,采用多点、多自由度配重方法平衡太阳翼展开过程中的重力,采用能量补偿方法减小展开过程中导轨摩擦力,如图 1所示.具体为:每块太阳翼板分别吊挂两个吊点,太阳翼连接架处吊挂一个吊点,且所有吊点均过质心线位置.滑车沿导轨运动,滑车上安装两个定滑轮,钢丝绳一端固定,另一端依次通过滑车上的两个定滑轮、滑车下部的一个动滑轮,桁架上的一个定滑轮,连接刹车配重机构.太阳翼展开过程中,在滑车沿导轨做水平方向的一维运动的同时,滑车上的动滑轮和刹车配重机构一起做竖直方向的一维运动;太阳翼展开到位时,传感器检测到铰链锁定信号,该信号触发刹车配重机构,刹车配重机构通过挤压钢丝实现配重快速制动,以快速消耗掉配重的能量,避免对太阳翼锁定、铰链冲击造成影响.

|
图 1 太阳翼板面水平展开试验方法 Figure 1 Method for horizontal deployable experiment of satellite solar array |
如图 2所示,太阳翼由3块基板和1个连接架组成,其中OA为连接架,AB、BC、CD分别为内板、中板、外板.设连接架长度为l0=2a0,质心偏心距为e0,各基板长度均为l=2a,且质心在基板几何中心,则运动学方程为
| $\left\{ \begin{align} & {{x}_{0}}={{a}_{0}}+{{e}_{0}}cos~\varphi ,{{y}_{0}}=2{{a}_{0}}-\left( {{a}_{0}}+{{e}_{0}} \right)sin~\varphi ; \\ & {{x}_{i}}=[2{{a}_{0}}+\left( 2i-1 \right)a]cos~\varphi ,\text{ }{{y}_{i}}=2{{a}_{0}}-\left( 2{{a}_{0}}-a \right)sin~\varphi . \\ \end{align} \right.$ | (1) |

|
图 2 太阳翼板面水平展开运动学模型 Figure 2 Kinematic model for horizontal deployable experiment of satellite solar array |
通过式(1)对时间t作一次和二次微分可得:
| $\left\{ \begin{align} & x_{0}^{'}=-\left( {{a}_{0}}+{{e}_{0}} \right)sin\varphi {{\varphi }^{'}}, \\ & y_{0}^{'}=-\left( {{a}_{0}}+{{e}_{0}} \right)cos\varphi {{\varphi }^{'}}, \\ & x_{i}^{'}=-[2{{a}_{0}}+2\left( i-1 \right)a]sin\varphi {{\varphi }^{\prime }}, \\ & y_{i}^{'}=-\left( 2{{a}_{0}}-a \right)cos\varphi {{\varphi }^{\prime }}. \\ \end{align} \right.$ |
| $\left\{ \begin{align} & x_{0}^{''}=-\left( {{a}_{0}}+{{e}_{0}} \right)[sin\varphi {{\varphi }^{''}}+cos~\varphi {{\left( {{\varphi }^{''}} \right)}^{2}}], \\ & y_{0}^{''}=-\left( {{a}_{0}}+{{e}_{0}} \right)[cos\varphi {{\varphi }^{\prime \prime }}-sin~\varphi {{\left( {{\varphi }^{\prime }} \right)}^{2}}], \\ & x_{i}^{''}=-[2{{a}_{0}}+\left( 2i-1 \right)a][sin\varphi {{\varphi }^{\prime \prime }}+cos~\varphi {{\left( {{\varphi }^{\prime }} \right)}^{2}}], \\ & y_{i}^{''}=-\left( 2{{a}_{0}}-a \right)[cos\varphi {{\varphi }^{\prime \prime }}-sin~\varphi {{\left( {{\varphi }^{\prime }} \right)}^{2}}]. \\ \end{align} \right.$ |
式中i=1,2,3.
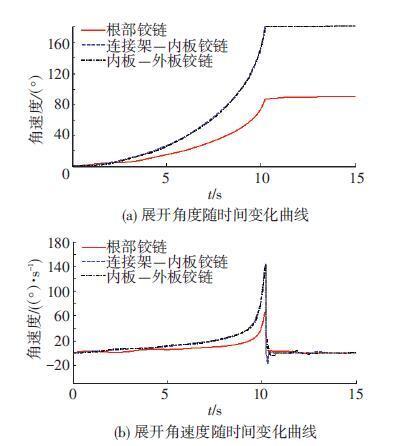
2.1.2 运动学仿真利用ADAMS多体动力学软件,建立太阳翼展开运动学模型,分析太阳翼展开运动,如图 3所示.由图 3可知,太阳翼在轨展开时间为10.765 s;根部铰链展开角度为90°,板间铰链展开角度为180°;在展开过程中铰链展开角度和展开角速度较平稳变化,在锁定瞬时铰链展开角度和展开角速度变化大.
|
图 3 太阳翼板面水平展开运动学仿真 Figure 3 Kinematic simulation for horizontal deployable experiment of satellite solar array |
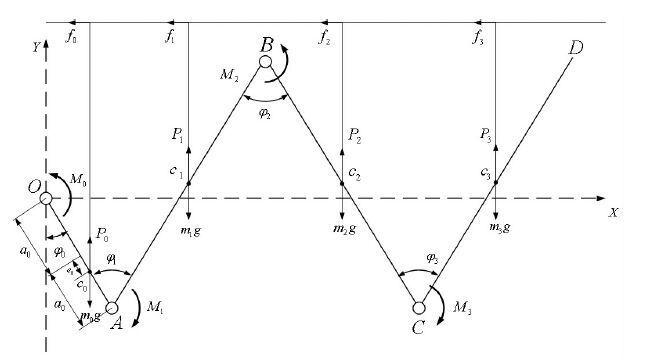
太阳翼地面展开试验时,主要受到铰链的驱动力、CCL的拉力,太阳翼的重力、吊绳的拉力、导轨的摩擦力,空气阻力等,其受力过程复杂.为便于分析,动力学建模时只考虑铰链的驱动力、太阳翼的惯性力、导轨的摩擦力,忽略CCL的拉力和空气阻力的影响,建立动力学方程,如图 4所示.
|
图 4 太阳翼板面水平展开动力学模型 Figure 4 Dynamics model for horizontal deployable experiment of satellite solar array |
根部铰接点O与板间铰接点A、B、C的驱动扭簧产生的驱动力矩为Tq分别为
| $\begin{align} & {{T}_{q0}}=T_{q0}^{0}-{{K}_{q0}}{{\varphi }_{0}}, \\ & {{T}_{qi}}=T_{qi}^{0}-{{K}_{qi}}{{\varphi }_{i-1}}+{{\varphi }_{i}},\left( i=0,1,2,3 \right). \\ \end{align}$ |
式中:Tqi0为初始太阳翼合拢状态各驱动扭簧的扭矩值,Kqi为弹性常数.
根据质心运动定理和相对于质心的动量矩定理建立微分方程为
| $\left\{ \begin{align} & \sum F_{i}^{X}-{{f}_{i}}={{m}_{i}}{{{\ddot{x}}}_{i}}, \\ & {{P}_{i}}\left( {{{\ddot{y}}}_{i}} \right)-{{m}_{i}}g+\sum F_{i}^{Y}={{m}_{i}}{{{\ddot{y}}}_{i}}, \\ & \frac{d}{dt}\left( {{J}_{Ci}}{{\omega }_{i}} \right)={{M}_{i}}+{{M}_{i+1}}+\sum {{M}_{C}}{{\left( F \right)}_{i}}+{{\left( -1 \right)}^{i}}{{f}_{i}}{{L}_{i}}{{y}_{i}}. \\ \end{align} \right.$ |
式中:JCi为连接架和各基板相对各自质心的转动惯量;∑FiX、∑FiY分别为作用在第i块基板上由铰链产生的约束反力之和,可由各板质心加速度求得;Pi为各质心吊点钢丝绳的拉力,可由配重重力与
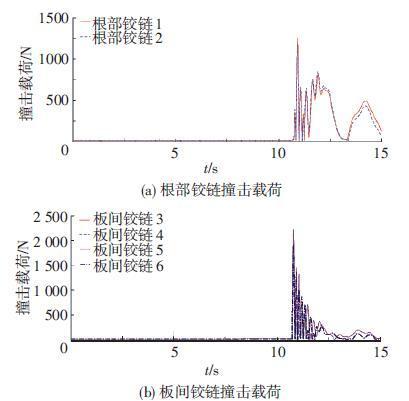
运用ADAMS软件分析太阳翼展开时铰链撞击载荷,以考核太阳翼铰链展开锁定的安全性,见图 5和表 1.由图 5和表 1可知:太阳翼在0~10.765 s的展开过程中,铰链撞击载荷基本为0;当太阳翼运动到10.765 s时,铰链受到较大撞击载荷,铰链撞击载荷最大值为2 235 N,出现在板间铰链3处.
|
图 5 铰链撞击载荷 Figure 5 Hinges impact load |
| 表 1 铰链撞击载荷峰值 Table 1 Peak value of hinges impact load |
太阳翼水平展开试验方法的影响因素主要有:摩擦力大小、配重质量偏差、吊挂质心偏差、空气阻力、钢丝绳柔性以及导轨变形等.本文采用控制变量法,分别对摩擦力、配重质量偏差、吊挂质心偏差进行分析,为后续试验验证提供指导.
3.1 摩擦力影响分析太阳翼水平展开试验时,摩擦力主要在钢丝绳与定滑轮间、钢丝绳与动滑轮间、滑车与导轨间存在,为分析方便,将其统一转化为滑车与导轨间的摩擦力,且不考虑配重质量偏差、吊挂质心偏差等影响,建立摩擦力误差数学模型,如图 6所示.

|
图 6 摩擦力影响数学模型 Figure 6 Mathematical model of friction |
以某一吊点为研究对象,由达郎贝尔原理可知
| $\overrightarrow{{{F}_{拉}}}+\overrightarrow{mg}+\overrightarrow{{{F}_{牵引}}}+\overrightarrow{{{f}_{摩}}}=0.$ |
式中:F牵引=F拉sin θ,f摩=u(F拉cos θ-mg)
对整个系统,其系统摩擦力和摩擦阻力做功为
| $\left\{ \begin{align} & ~\sum\limits_{i=0}^{3}{{{f}_{摩i}}}=\sum\limits_{i=0}^{3}{{{u}_{i}}}({{F}_{拉i}}cos~{{\theta }_{i}}-{{m}_{i}}g), \\ & {{W}_{牵引阻力}}=\sum\limits_{i=0}^{3}{{{F}_{牵引i}}}{{l}_{i}}cos~{{\varphi }_{i}}=\sum\limits_{i=0}^{3}{{{F}_{拉i}}}sin~{{\theta }_{i}}{{l}_{i}}cos~{{\varphi }_{i}}, \\ \end{align} \right.$ |
进一步,针对运动学仿真模型进行摩擦力影响因素分析,仿真结果见表 2.
| 表 2 摩擦力对水平展开试验的影响 Table 2 Influence of friction on horizontal deployable experiment |
由误差模型及表 2可知:1) 太阳翼带动滑车一起运动,由于导轨摩擦力的存在,导致滑车运动滞后于太阳翼吊点运动;2) 当导轨摩擦力增大时,太阳翼展开锁定时间将延长.
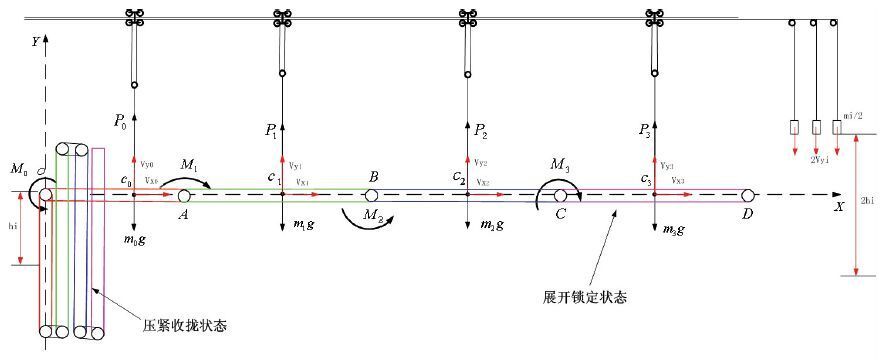
3.2 配重质量影响分析配重质量是影响太阳翼水平展开试验的主要因素,选取各板的初始质心位置为坐标原点,建立配重质量偏差数学模型,如图 7所示.
|
图 7 配重质量偏差数学模型 Figure 7 Mathematical model of mass deviation |
太阳翼分收拢、展开两个状态,采用能量法分析,太阳翼的能量变化为
| $\begin{align} & {{W}_{太阳翼}}={{T}_{太阳翼}}+{{V}_{太阳翼}}=\frac{1}{2}\sum\limits_{i=0}^{3}{{{J}_{i}}\alpha _{i}^{2}}+\frac{1}{2}\sum\limits_{i=0}^{3}{{{m}_{i}}v_{xi}^{2}}+ \\ & \frac{1}{2}\sum\limits_{i=0}^{3}{{{m}_{i}}v_{yi}^{2}}+\sum\limits_{i=0}^{3}{{{m}_{i}}g{{h}_{i}}}. \\ \end{align}$ | (2) |
配重块的能量变化为
| ${{W}_{配重块}}={{T}_{配重块}}-{{V}_{配重块}}=\sum\limits_{i=0}^{3}{{{m}_{i}}v_{yi}^{2}}-\sum\limits_{i=0}^{3}{{{m}_{i}}g{{h}_{i}},}$ | (3) |
则由能量守恒定律,联立式(2)~(3)得:
| $\begin{align} & {{T}_{qi}}={{W}_{太阳翼}}+{{W}_{配重块}}={{T}_{太阳翼}}+{{V}_{太阳翼}}+{{T}_{配重块}}-{{V}_{配重块}}= \\ & \frac{1}{2}\sum\limits_{i=0}^{3}{{{J}_{i}}\alpha _{i}^{2}}+\frac{1}{2}\sum\limits_{i=0}^{3}{{{m}_{i}}v_{xi}^{2}}+\frac{1}{2}\sum\limits_{i=0}^{3}{{{m}_{i}}v_{yi}^{2}}+ \\ & \sum\limits_{i=0}^{3}{{{m}_{i}}g{{h}_{i}}}+\sum\limits_{i=0}^{3}{{{m}_{i}}v_{yi}^{2}}-\sum\limits_{i=0}^{3}{{{m}_{i}}g{{h}_{i}}}=\frac{1}{2}\sum\limits_{i=0}^{3}{{{J}_{i}}\alpha _{i}^{2}}+ \\ & \frac{1}{2}\sum\limits_{i=0}^{3}{{{m}_{i}}v_{xi}^{2}}+\frac{1}{2}\sum\limits_{i=0}^{3}{{{m}_{i}}v_{yi}^{2}}+\sum\limits_{i=0}^{3}{{{m}_{i}}v_{yi}^{2}}. \\ \end{align}$ |
针对运动学模型开展配重质量对水平展开试验的影响因素分析,仿真结果见表 3.
| 表 3 配重质量对水平展开试验的影响 Table 3 Influence of mass deviation on horizontal deployable experiment |
由误差模型及表 3可知:1)水平展开试验时,太阳翼扭簧释放的能量转化为太阳翼水平、竖直两方向的动能、太阳翼的转动动能和配重块的动能;2)单点配重质量影响展开试验时间.当单点配重质量减少时,展开试验时间延长;当单点配重质量增加时,展开试验时间缩短;3)当单点配重质量偏差大于±30 g时,太阳翼无法展开锁定.
3.3 吊挂质心影响分析太阳翼吊挂质心对水平展开试验也有重要影响,建立吊挂质心偏差数学模型,如图 8所示.

|
图 8 吊挂质心偏差数学模型 Figure 8 Mathematical model of centroid deviation |
假设太阳翼各板质心位置偏差为ei,对各转动轴取力矩,则由质心位置偏差引起的能量损耗为
| ${{W}_{质心偏差}}=\sum\limits_{i=0}^{3}{({{P}_{i}}-{{m}_{i}}g)}{{e}_{i}}sin~\theta \cdot {{l}_{i}}.$ |
针对运动学模型开展吊挂质心偏差对水平展开试验的影响因素分析,仿真结果见表 4.
| 表 4 吊挂质心偏差对水平展开试验的影响 Table 4 Influence of centroid deviation on horizontal deployable experiment |
由误差模型及表 4可知:1) 吊挂质心位置影响水平展开试验时间.当吊挂质心偏差增大时,质心偏差引起的能量损耗增加,水平展开锁定时间延长;2) 当吊挂质心偏差大于30 mm时,其产生的附加力矩会阻止太阳翼的展开,太阳翼无法展开锁定.
4 试验验证选取某型号卫星太阳翼开展试验验证,考核其展开运动学、展开动力学特性,验证太阳翼水平展开试验方法的可行性.
4.1 运动学特性测试针对吊点进行展开过程中运动学特性分析,如图 9所示,在太阳翼同一侧贴8个编码点,用辰维MPS实时工业摄影测量系统对太阳翼展开过程进行实时监测,该测量系统测量范围≥8 000 mm×1 500 mm,测量精度优于0.5 mm,测量速度≥10 帧/s.

|
图 9 太阳翼吊点运动轨迹测量方法 Figure 9 Kinematic test method for horizontal deployable experiment |
如图 10所示,选择内板吊点分析其运动特性,从测得的各吊点“s-t”、“v-t”、“a-t”曲线,并与仿真结果比对,见表 5.

|
图 10 内板吊点运动特性测量 Figure 10 Kinematic test rest for horizontal deployable experiment |
| 表 5 仿真与测试结果比对 Table 5 Comparison on simulation and test results |
通过表 5可知: 1)由“s-t”曲线可知,各吊点位移运动规律与在轨仿真相同,同时各点在展开过程中运动较平稳,没有出现位移突变;2)由“v-t”曲线可知,各吊点X方向最大速度中外板(0.50 m/s)>内板(0.25 m/s)>连接架(0.08 m/s);Y方向最大速度中连接架(0.15 m/s)>内板(0.06 m/s)>外板(0.05 m/s).与仿真结果相比,其趋势相同,数值小于在轨值,这是由地面展开试验的摩擦力、风阻等造成的,合乎逻辑;3)由“a-t”曲线可知,X方向最大加速度中k外板(0.050 m/s2)>内板(0.020 m/s2)>连接架(0.015 m/s2);Y方向最大加速度中连接架(0.020 m/s2)>内板(0.005 m/s2)>外板(0.005 m/s2).与仿真结果相比,其趋势相同,数值小于在轨值,原因与2)相同;4)由于地面摩擦力和空气阻力的影响,展开试验测试时间大于在轨仿真值.对比试验与仿真结果说明,水平展开试验各点运动规律与在轨展开运动规律相似.
4.2 铰链冲击载荷测试铰链冲击载荷测试共在6个位置布置传感器,测量X、Y、Z这3个方向的冲击响应,共计18个通道,分别采集各测点的加速度信号,各测点的测试与仿真结果对比见表 6.
| 表 6 测试与仿真结果比对 Table 6 Comparison on simulation and test results |
由表 6可知:1)铰链的实测锁定顺序与仿真锁定顺序相同.实测锁定先后顺序为外板、内板、连接架,外内板时差约500 ms,内板与连接架时差10 ms;仿真锁定先后顺序为外板、内板、连接架,外内板时差约60 ms,内板与连接架时差约150 ms.2)铰链实测冲击载荷均小于仿真值.铰链实测冲击载荷大小依次为5、6点>1、2点>3、4点.3)铰链实测峰值震荡时间均小于仿真值.
5 结 论1) 该方法要求太阳翼各吊点配重质量偏差小于30 g、各吊点吊挂质心偏差小于30 mm、系统摩擦力越小越好,满足铰链锁定冲击载荷安全性要求.
2) 试验表明,太阳翼水平展开运动规律与在轨展开运动规律相吻合,满足卫星太阳翼展开试验要求.
3) 相比传统展开试验方法,该方法避免了卫星姿态翻转,确保了光学载荷指向精度,节省了展开试验准备时间.
| [1] |
马兴瑞, 于登云, 孙京, 等. 空间飞行器展开与驱动机构研究进展[J].
宇航学报,2006, 27 (6) : 1123-1131.
DOI: 10.3321/j.issn:1000-1328.2006.06.001 MA Xingrui, YU Dengyun, SUN Jing, et al. The researching evolvement of spacecraft deployment and driving mechanism[J]. Journal of Astronautics,2006, 27 (6) : 1123-1131. DOI: 10.3321/j.issn:1000-1328.2006.06.001 (  0) 0)
|
| [2] |
从强. 空间机构地面重力补偿设备跟踪研究[J].
航天器环境工程,2012, 29 (1) : 92-99.
DOI: 10.3969/j.issn.1673-1379.2012.01.020 CONG Qiang. An investigation into gravity compensation equipment for space mechanisms[J]. Spacecraft Environment Engineering,2012, 29 (1) : 92-99. DOI: 10.3969/j.issn.1673-1379.2012.01.020 (  0) 0)
|
| [3] |
任守志, 刘立平. 零重力试验装置对太阳翼展开的影响分析[J].
航天器工程,2008, 17 (6) : 73-78.
DOI: 10.3969/j.issn.1673-8748.2008.06.011 REN Shouzhi, LIU Liping. Influence of the Zero-gravity test facil ity on the solar array' s deployment test[J]. Spacecraft Engineering,2008, 17 (6) : 73-78. DOI: 10.3969/j.issn.1673-8748.2008.06.011 (  0) 0)
|
| [4] |
SCHULTHEI D. Gravity compensation of deployable solar arrays for small spacecraft[D]. Cambridge: University of Cambridge, 2003.
( 0) 0)
|
| [5] |
ALAN J P, BRIAN R S. Spacecraft solar array technology trends[J].
IEEE Aerospace and Electronic Systems Magazine,2011, 26 (8) : 17-28.
DOI: 10.1109/AERO.1998.686813 ( 0) 0)
|
| [6] |
ZUCKERMANDEL J W, ENGER S, GUPTA N. Design, build, and testing of TacSat thin film solar arrays[C] // Proceedings of the 4th International Energy Conversion Engineering Conference. San Diego: AIAA, 2006: 4198-4210.
( 0) 0)
|
| [7] |
NOBUAKI N, SHOICHI L, YOSHIAKI T, et al. Design and experimental production of small deployable mesh type reflector antenna [C]//Proceedings of the 44th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference. Norfolk,VA: AIAA, 2013:1581-1589.
( 0) 0)
|
| [8] |
CAMPBELL D, BARRETT R,LAKE M, et al. Development of a novel, passively deployed solar array[C]//Proceedings of the 47th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference. Newport, RI: AIAA, 2006: 2080-2087.
( 0) 0)
|
| [9] |
SANTONI F, PIERGENTILI F, DONATI S, et al. Designing and realization of an innovative deployable solar panel system for cubesats[C] //Proceedings of the 63rd International Astronautical Congress. Naples, Italy: IAC, 2012: 7119-7127.
( 0) 0)
|
| [10] |
SPENCE B, WHITE S, WILDER N, et al. Next generation ultraflex solar array for nasa’s new millennium program space technology 8[C] //2005 IEEE Aerospace Conference. Big Sky: IEEE,2005:1539-1551.DOI:10.1109/AERO.2005.1559374.
( 0) 0)
|
| [11] |
郭其威, 苟永杰, 何岗. 太阳电池阵地面展开仿真技术研究与试验验证[J].
空间科学学报,2009, 29 (1) : 59-63.
DOI: 10.11728/cjss2009.01.059 GUO Qiwei, GOU Yongjie, HE Gang. Ground dynamics experiment of simulation and solar array[J]. Chinese Journal of Space Science,2009, 29 (1) : 59-63. DOI: 10.11728/cjss2009.01.059 (  0) 0)
|
| [12] |
王晛, 陈天智, 柴洪友. 太阳翼地面展开锁定的动力学仿真分析[J].
航天器工程,2011, 20 (3) : 86-92.
DOI: 10.3969/j.issn.1673-8478.2011.03.014 WANG Xian, CHEN Tianzhi, CHAI Hongyou. Dynamics simulation analysis of solar array ground deployment and locking[J]. Spacecraft Engineering,2011, 20 (3) : 86-92. DOI: 10.3969/j.issn.1673-8478.2011.03.014 (  0) 0)
|
| [13] |
刘锦阳, 洪嘉振. 卫星太阳电池阵的钢-柔耦合动力学[J].
空间科学学报,2004, 24 (5) : 367-372.
LIU Jinyang, HONG Jiazhen. Rigid-Flexible coupling dynamics of satellite solar battery[J]. Chinese Journal of Space Science,2004, 24 (5) : 367-372. (  0) 0)
|
 2016, Vol. 48
2016, Vol. 48


