2. 北京空间飞行器总体设计部,北京100094
2. Beijing Institute of Spacecraft System Engineering, Beijing 100094, China
现代航天器的功能需求对卫星的大角度快速机动能力提出更高的要求,以提高卫星获取信息的能力,这个能力不仅体现在获取信息的快速性上[1],还体现在信息获取的多样性上(如立体成像,拼接成像等)[2-3].在一些非沿迹成像[4]、地面动目标跟踪这些工作模式在卫星快速机动的基础上,还要求卫星在机动过程中保持高精度的姿态跟踪能力.飞行器快速机动与高精度跟踪是一对矛盾的控制要求,对飞行器的姿态控制性能提出了很高的要求,特别是执行机构的力矩特征.航天器常用的执行机构有飞轮、推力器以及控制力矩陀螺(CMG).飞轮能提供精确的控制力矩,但输出力矩较小;推力器能提供大但粗糙的力矩,且消耗推进剂;CMG能提供较大的力矩,但需多个配合使用[5-6].按照目前国内外使用这些执行机构的情况,无论是从不同使用场景或者备份的角度,一般飞行器都会携带多个不同种类的执行机构[7],因此,国内外很多学者都提出采用联合多个执行机构进行控制的理论方法,期望发挥各个执行的优点[8-9].针对飞轮与推力器联合使用的问题,文献[10]提出使用推力器产生快速机动所需的大力矩,同时采用飞轮进行姿态跟踪偏差的修正,并设计了变结构控制器对推力器不准确所带来的干扰进行抑制.随着加工技术及工艺的提高,在不久的未来将会有越来越多的飞行器采用CMG作为快速机动的执行机构,但CMG的使用过程中会出现奇异现象[11].虽然国内外学者提出各种避免/逃脱奇异性的方法,但这些方法多以牺牲控制精度为代价[12].唯一一种保障精度的方案则依赖变速控制力矩陀螺(VSCMG)[13],但其机构复杂,且转子转速降幅有限,过低的转速会破坏力矩放大的特性,目前还很难实际应用.因此有学者就提出采用CMG和飞轮联合使用的方式, 文献[14]提出在敏捷卫星快速机动过程中采用CMG加速,在稳定阶段采用飞轮进行姿态控制偏差修正以及高精度的稳定控制.针对这些方法无法解决姿态机动中的控制精度的问题,文献[15]提出了使用CMG进行粗控,利用飞轮进行补偿控制的方式取得良好的效果.文献[16]提出利用奇异值分解确定CMG的奇异方向,并将此方向的力矩指令分配给飞轮,从而达到避开奇异的效果.
上述联合执行机构的使用能够很好地解决力矩输出与精确控制之间的矛盾问题,但均没有考虑执行机构安装不确定性给联合执行机构的使用所带来的影响[17].本文基于这一考虑,采取设计多输入多输出的自适应控制器处理这一问题.首先, 建立携带变速控制力矩陀螺的卫星动力学方程,在此基础上建立联合CMG和飞轮作为执行机构的卫星姿态控制模型;然后, 针对具有执行机构安装偏差的卫星模型进行自适应控制律设计;最后,针对所提出的算法进行数学仿真以验证其有效性.
1 动力学模型建立为后续的控制设计的需要建立卫星动力学模型.控制对象为携带多个CMG和飞轮的敏捷卫星,为此基于VSCMG建立一个通用的动力学模型.
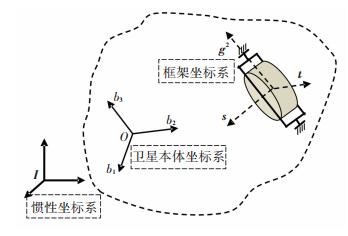
携带VSCMG的卫星模型示意图如图 1所示,其中框架坐标系(g, s, t)定义为:g为框架轴转动的方向,s为转子轴方向,t与g和s构成右手系, 则VSCMG相对于卫星本体系的方向余弦矩阵可表示为
|
图 1 携带一个VSCMG卫星的坐标系定义 Figure 1 The coordination definition for the satellite with one VSCMG |
| $ \boldsymbol{C}=\left[\boldsymbol{g}\ \boldsymbol{s}\ \boldsymbol{t} \right]. $ |
VSCMG的框架和转子的转动惯量在卫星本体坐标系可表示为
| $ {{\boldsymbol{J}}_{g}}=\boldsymbol{C}{{\boldsymbol{I}}_{g}}{{\boldsymbol{C}}^{\text{T}}}, \ \ \ \ {{\boldsymbol{J}}_{w}}=\boldsymbol{C}{{\boldsymbol{I}}_{w}}{{\boldsymbol{C}}^{\text{T}}}. $ |
式中,Ig=diag[Ig1, Ig2, Ig3]、Iw=diag[Iw1, Iw2, Iw3]分别表示在框架坐标系中表示的VSCMG的框架和转子的转动惯量.在框架坐标系和本体坐标系下表示的卫星本体角速度具有以下关系:
| $ \boldsymbol{\omega} =\boldsymbol{C}{\boldsymbol{{\omega }}_{g}}, $ |
式中ω、ωg分别表示在本体坐标系和框架坐标系下表示的卫星本体角速度.令Js表示包括把VSCMG看做是点质量在内的卫星本体转动惯量,则卫星本体的角动量hs可以表示为
| $ {{\boldsymbol{h}}_{s}}={{\boldsymbol{J}}_{s}}\boldsymbol{\omega} . $ |
首先考虑只携带一个VSCMG的卫星模型.使用
| $ {\mathit{\boldsymbol{h}}_g} = \mathit{\boldsymbol{C}}{\mathit{\boldsymbol{I}}_g}\left( {{\mathit{\boldsymbol{\omega }}_g} + {{\mathit{\boldsymbol{\dot \gamma }}}_g}} \right). $ |
VSCMG的角动量hw表示为
| $ {\mathit{\boldsymbol{h}}_w} = \mathit{\boldsymbol{C}}{\mathit{\boldsymbol{I}}_w}\left( {{\mathit{\boldsymbol{\omega }}_g} + {{\mathit{\boldsymbol{\dot \gamma }}}_g} + {{\mathit{\boldsymbol{\tilde \omega }}}_g}} \right). $ |
定义Ic=Ig+Iw,则卫星整体的角动量表示为
| $ \mathit{\boldsymbol{h}} = \left( {{\mathit{\boldsymbol{J}}_s} + \mathit{\boldsymbol{C}}{\mathit{\boldsymbol{I}}_c}{\mathit{\boldsymbol{C}}^{\rm{T}}}} \right)\mathit{\boldsymbol{\omega }} + \mathit{\boldsymbol{C}}{\mathit{\boldsymbol{I}}_c}{{\mathit{\boldsymbol{\dot \gamma }}}_g} + \mathit{\boldsymbol{C}}{\mathit{\boldsymbol{I}}_w}{{\mathit{\boldsymbol{\tilde \omega }}}_g}, $ |
其中
| $ \mathit{\boldsymbol{C}}{\mathit{\boldsymbol{I}}_c}{\mathit{\boldsymbol{C}}^{\rm{T}}} = {\mathit{\boldsymbol{I}}_{csi}}\mathit{\boldsymbol{s}}{\mathit{\boldsymbol{s}}^{\rm{T}}} + {\mathit{\boldsymbol{I}}_{cti}}\mathit{\boldsymbol{t}}{\mathit{\boldsymbol{t}}^{\rm{T}}} + {\mathit{\boldsymbol{I}}_{cgi}}\mathit{\boldsymbol{g}}{\mathit{\boldsymbol{g}}^{\rm{T}}}. $ |
根据VSCMG的特征可知
| $ \mathit{\boldsymbol{C}}{\mathit{\boldsymbol{I}}_c}{{\mathit{\boldsymbol{\dot \gamma }}}_g} = {\mathit{\boldsymbol{I}}_{cgi}}\mathit{\boldsymbol{\dot \gamma g, }}\;\;\;\mathit{\boldsymbol{C}}{\mathit{\boldsymbol{I}}_w}{{\mathit{\boldsymbol{\tilde \omega }}}_g} = {\mathit{\boldsymbol{I}}_{wsi}}\mathit{\boldsymbol{\tilde \omega s, }} $ |
故卫星整体角动量可以改写为
| $ \begin{array}{l} \mathit{\boldsymbol{h = }}\left( {{\mathit{\boldsymbol{J}}_s} + {\mathit{\boldsymbol{I}}_{csi}}\mathit{\boldsymbol{s}}{\mathit{\boldsymbol{s}}^{\rm{T}}} + {\mathit{\boldsymbol{I}}_{cti}}\mathit{\boldsymbol{t}}{\mathit{\boldsymbol{t}}^{\rm{T}}} + {\mathit{\boldsymbol{I}}_{cgi}}\mathit{\boldsymbol{g}}{\mathit{\boldsymbol{g}}^{\rm{T}}}} \right)\mathit{\boldsymbol{\omega }} + \\ \;\;\;\;\;\;{\mathit{\boldsymbol{I}}_{cgi}}\mathit{\boldsymbol{\dot \gamma g + }}{\mathit{\boldsymbol{I}}_{wsi}}\mathit{\boldsymbol{\tilde \omega s}}, \end{array} $ |
则可以得到携带L个VSCMG的卫星角动量为
| $ \mathit{\boldsymbol{h}} = \mathit{\boldsymbol{J\omega }} + {\mathit{\boldsymbol{A}}_g}{\mathit{\boldsymbol{I}}_{cg}}\mathit{\boldsymbol{\dot \gamma }} + {\mathit{\boldsymbol{A}}_s}{\mathit{\boldsymbol{I}}_{ws}}\mathit{\boldsymbol{\tilde \omega }}, $ | (1) |
| $ \mathit{\boldsymbol{J}} = {\mathit{\boldsymbol{J}}_s} + {\mathit{\boldsymbol{A}}_s}{\mathit{\boldsymbol{I}}_{cs}}\mathit{\boldsymbol{A}}_s^{\rm{T}} + {\mathit{\boldsymbol{A}}_t}{\mathit{\boldsymbol{I}}_{ct}}\mathit{\boldsymbol{A}}_t^{\rm{T}} + {\mathit{\boldsymbol{A}}_g}{\mathit{\boldsymbol{I}}_{cg}}\mathit{\boldsymbol{A}}_g^{\rm{T}}, $ | (2) |
其中
| $ \begin{array}{l} \mathit{\boldsymbol{\gamma }} = {\left[{{\mathit{\boldsymbol{\gamma }}_1}, {\mathit{\boldsymbol{\gamma }}_2}, \cdots, {\mathit{\boldsymbol{\gamma }}_L}} \right]^{\rm{T}}}, \mathit{\boldsymbol{\tilde \omega }} = {\left[{{{\mathit{\boldsymbol{\tilde \omega }}}_1}, {{\mathit{\boldsymbol{\tilde \omega }}}_2}, \cdots, {{\mathit{\boldsymbol{\tilde \omega }}}_L}} \right]^{\rm{T}}}, \\ {\mathit{\boldsymbol{A}}_s} = \left[{{\mathit{\boldsymbol{s}}_1}, {\mathit{\boldsymbol{s}}_2}, \cdots, {\mathit{\boldsymbol{s}}_L}} \right], {\mathit{\boldsymbol{A}}_t} = \left[{{\mathit{\boldsymbol{t}}_1}, {\mathit{\boldsymbol{t}}_2}, \cdots, {\mathit{\boldsymbol{t}}_L}} \right], \\ {\mathit{\boldsymbol{A}}_g} = \left[{{\mathit{\boldsymbol{g}}_1}, {\mathit{\boldsymbol{g}}_2}, \cdots, {\mathit{\boldsymbol{g}}_L}} \right], \end{array} $ |
且
| $ \begin{array}{l} {\mathit{\boldsymbol{A}}_s} = {\mathit{\boldsymbol{A}}_{s0}}{\left[{\cos \mathit{\boldsymbol{\gamma }}} \right]^d} + {\mathit{\boldsymbol{A}}_{t0}}{\left[{\sin \mathit{\boldsymbol{\gamma }}} \right]^d}, \\ {\mathit{\boldsymbol{A}}_t} = {\mathit{\boldsymbol{A}}_{t0}}{\left[{\cos \mathit{\boldsymbol{\gamma }}} \right]^d} + {\mathit{\boldsymbol{A}}_{s0}}{\left[{\sin \mathit{\boldsymbol{\gamma }}} \right]^d}. \end{array} $ | (3) |
式中:
| $ {{\mathit{\boldsymbol{\dot A}}}_s} = {\mathit{\boldsymbol{A}}_t}{\left[{\mathit{\boldsymbol{\dot \gamma }}} \right]^d}, {{\mathit{\boldsymbol{\dot A}}}_t} = - {\mathit{\boldsymbol{A}}_s}{\left[{\mathit{\boldsymbol{\dot \gamma }}} \right]^d}. $ |
对卫星整体角动量式(2)求导可得到:
| $ \mathit{\boldsymbol{\dot J}} = {\mathit{\boldsymbol{A}}_t}{\left[{\mathit{\boldsymbol{\dot \gamma }}} \right]^d}\left( {{\mathit{\boldsymbol{I}}_{cs}} - {\mathit{\boldsymbol{I}}_{ct}}} \right)\mathit{\boldsymbol{A}}_s^{\rm{T}} + {\mathit{\boldsymbol{A}}_s}{\left[{\mathit{\boldsymbol{\dot \gamma }}} \right]^d}\left( {{\mathit{\boldsymbol{I}}_{cs}} - {\mathit{\boldsymbol{I}}_{ct}}} \right)\mathit{\boldsymbol{A}}_t^{\rm{T}}, $ |
进一步,卫星动力学方程可以表示为
| $ \begin{array}{l} \left( {{\mathit{\boldsymbol{A}}_t}{{\left[{\mathit{\boldsymbol{\dot \gamma }}} \right]}^d}\left( {{\mathit{\boldsymbol{I}}_{cs}} - {\mathit{\boldsymbol{I}}_{ct}}} \right)\mathit{\boldsymbol{A}}_s^{\rm{T}} + {\mathit{\boldsymbol{A}}_s}{{\left[{\mathit{\boldsymbol{\dot \gamma }}} \right]}^d}\left( {{\mathit{\boldsymbol{I}}_{cs}} - {\mathit{\boldsymbol{I}}_{ct}}} \right)\mathit{\boldsymbol{A}}_t^{\rm{T}}} \right)\mathit{\boldsymbol{\omega + }}\\ \mathit{\boldsymbol{J\dot \omega + }}{\mathit{\boldsymbol{A}}_g}{\mathit{\boldsymbol{I}}_{cg}}\mathit{\boldsymbol{\ddot \gamma + }}{\mathit{\boldsymbol{A}}_t}{\mathit{\boldsymbol{I}}_{ws}}{\left[{\mathit{\boldsymbol{\dot \omega }}} \right]^d}\mathit{\boldsymbol{\dot \gamma }} + {\mathit{\boldsymbol{A}}_s}{\mathit{\boldsymbol{I}}_{ws}}\mathit{\boldsymbol{\dot \omega }} + \\ {\mathit{\boldsymbol{\omega }}^ \times }\left( {\mathit{\boldsymbol{J\omega }} + {\mathit{\boldsymbol{A}}_g}{\mathit{\boldsymbol{I}}_{cg}}\mathit{\boldsymbol{\dot \gamma }} + {\mathit{\boldsymbol{A}}_s}{\mathit{\boldsymbol{I}}_{ws}}\mathit{\boldsymbol{\dot \omega }}} \right) = 0 \end{array} $ |
为便于后续控制系统的设计,进行以下合理假设:由于VSCMG的转动惯量相对于卫星本体是小量,则卫星本体的转动惯量变化律可以忽略;ω和
| $ \boldsymbol{J\dot{\omega }}+{\boldsymbol{{\omega }}^{\times }}\boldsymbol{J\omega} +{\boldsymbol{{\omega }}^{\times }}{{\boldsymbol{A}}_{s}}{{\boldsymbol{I}}_{ws}}\boldsymbol{\dot{\omega }}=-{{\boldsymbol{A}}_{t}}{{\boldsymbol{I}}_{ws}}{{{\boldsymbol{\tilde{\omega }}}}^{d}}\boldsymbol{\gamma} -{{\boldsymbol{A}}_{s}}{{\boldsymbol{I}}_{ws}}\boldsymbol{\dot{\tilde{\omega }}}. $ | (4) |
这里讨论的是CMG和飞轮的联合执行机构控制问题,对上述建立的动力学方程式(4)进行适当改造(不妨假设卫星携带M个CMG与N个飞轮,这里L=M+N):令其中M个VSCMG的转子转速为恒定值且
| $ \begin{align} & \boldsymbol{J\dot{\omega }}+{\boldsymbol{{\omega }}^{\times }}\boldsymbol{J\omega} +{\boldsymbol{{\omega }}^{\times }}\left( {{\mathsf{A}}_{\mathsf{cs}}}{{\mathsf{I}}_{\mathsf{cws}}}{{{\boldsymbol{\tilde{\omega }}}}_{c}}+{{\mathsf{A}}_{\mathsf{ws}}}{{\mathsf{I}}_{\mathsf{wws}}}{{{\boldsymbol{\tilde{\omega }}}}_{w}} \right)= \\ & -{{\boldsymbol{A}}_{ct}}{{\boldsymbol{I}}_{cws}}\boldsymbol{\tilde{\omega }}_{c}^{d}{{{\boldsymbol{\dot{\gamma }}}}_{c}}-{{\boldsymbol{A}}_{ws}}{{\boldsymbol{I}}_{wws}}{{{\boldsymbol{\dot{\tilde{\omega }}}}}_{w}}. \\ \end{align} $ |
式中下角标c、w分别为CMG或飞轮所对应的量.
为便于后续控制系统设计及表达方便,令
| $ \boldsymbol{J\dot{\omega }}+{\boldsymbol{{\omega }}^{\times }}\boldsymbol{h}+{{\boldsymbol{A}}_{ct}}{{\boldsymbol{H}}_{cw}}\boldsymbol{\dot{\gamma }}+{{\boldsymbol{A}}_{ws}}{{\boldsymbol{I}}_{wws}}\boldsymbol{\dot{\tilde{\omega }}}=0 $ | (5) |
本文利用无冗余的修正罗德里格参数(MRP)表示姿态,方向余弦矩阵C与MRP之间的转换关系为
| $ \mathit{\boldsymbol{C}}\left( \mathit{\boldsymbol{\sigma }} \right) = \mathit{\boldsymbol{I}} - \frac{{4\left( {1 - {\mathit{\boldsymbol{\sigma }}^{\rm{T}}}\mathit{\boldsymbol{\sigma }}} \right)}}{{{{\left( {1 + {\mathit{\boldsymbol{\sigma }}^{\rm{T}}}\mathit{\boldsymbol{\sigma }}} \right)}^2}}}{\mathit{\boldsymbol{\sigma }}^ \times } + \frac{8}{{{{\left( {1 + {\mathit{\boldsymbol{\sigma }}^{\rm{T}}}\mathit{\boldsymbol{\sigma }}} \right)}^2}}}{\left( {{\mathit{\boldsymbol{\sigma }}^ \times }} \right)^2}. $ |
式中:σ×是σ的叉乘算子,I为单位矩阵.基于MRP的卫星姿态运动学方程为
| $ \mathit{\boldsymbol{\dot \sigma }} = \mathit{\boldsymbol{G}}\left( \mathit{\boldsymbol{\sigma }} \right)\mathit{\boldsymbol{\omega }}, $ | (6) |
其中G(σ)为
| $ \mathit{\boldsymbol{G}}\left( \mathit{\boldsymbol{\sigma }} \right) = \frac{1}{4}\left( {\left( {1 - {\mathit{\boldsymbol{\sigma }}^{\rm{T}}}\mathit{\boldsymbol{\sigma }}} \right)\mathit{\boldsymbol{I}} + 2{\mathit{\boldsymbol{\sigma }}^ \times } + 2\mathit{\boldsymbol{\sigma }}{\mathit{\boldsymbol{\sigma }}^{\rm{T}}}} \right). $ |
对式(6)进行微分可得
| $ \mathit{\boldsymbol{\ddot \sigma }} = \mathit{\boldsymbol{\dot G}}\left( {\mathit{\boldsymbol{\sigma }}, \mathit{\boldsymbol{\dot \sigma }}} \right)\mathit{\boldsymbol{\omega }} + \mathit{\boldsymbol{G}}\left( \mathit{\boldsymbol{\sigma }} \right)\mathit{\boldsymbol{\tilde \omega, }} $ |
其中
| $ \mathit{\boldsymbol{\dot G}}\left( {\mathit{\boldsymbol{\sigma }}, \mathit{\boldsymbol{\dot \sigma }}} \right) = \frac{1}{2}\left( {{{\mathit{\boldsymbol{\dot \sigma }}}^ \times } + \mathit{\boldsymbol{\dot \sigma }}{\mathit{\boldsymbol{\sigma }}^{\rm{T}}} + \mathit{\boldsymbol{\sigma }}{{\mathit{\boldsymbol{\dot \sigma }}}^{\rm{T}}} - {{\mathit{\boldsymbol{\dot \sigma }}}^{\rm{T}}}\mathit{\boldsymbol{\sigma I}}} \right), $ |
进而可以得到:
| $ \mathit{\boldsymbol{\dot \omega }} = {\mathit{\boldsymbol{G}}^{ - 1}}\left( {\mathit{\boldsymbol{\ddot \sigma }} - \mathit{\boldsymbol{\dot G\omega }}} \right). $ | (7) |
此外,由于在轨卫星受到的外界干扰力矩在10-5 N·m量级,而卫星在执行机动任务的时间一般在5 min左右,则在这短时间内由外界干扰引起的卫星角动量变化作用非常小,则可认为整星角动量在惯性系下的是保守的.使用HI表示在惯性系下表示的整星角动量,则HI和式(5)中h之间的关系可以表示为
| $ \mathit{\boldsymbol{h = C}}\left( \mathit{\boldsymbol{\sigma }} \right){\mathit{\boldsymbol{H}}_{\rm{I}}}. $ |
将式(7)代入式(5)可得
| $ \mathit{\boldsymbol{\ddot \sigma }} = {\mathit{\boldsymbol{F}}^*}\left( {\mathit{\boldsymbol{\sigma }}, \mathit{\boldsymbol{\dot \sigma }}} \right) - {\mathit{\boldsymbol{G}}^*}\left( {\mathit{\boldsymbol{\sigma }}, \mathit{\boldsymbol{\dot \sigma }}} \right)\mathit{\boldsymbol{u}}, $ | (8) |
其中:
| $ \begin{array}{l} {\mathit{\boldsymbol{F}}^*}\left( {\mathit{\boldsymbol{\sigma }}, \mathit{\boldsymbol{\dot \sigma }}} \right) = {\mathit{\boldsymbol{H}}^{* - 1}}\left( {{\mathit{\boldsymbol{H}}^*}\mathit{\boldsymbol{\dot G}}{\mathit{\boldsymbol{G}}^{ - 1}}\mathit{\boldsymbol{\dot \sigma }}} \right.\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left. {{\mathit{\boldsymbol{G}}^{ - {\rm{T}}}}{\mathit{\boldsymbol{\omega }}^ \times }\mathit{\boldsymbol{C}}\left( \mathit{\boldsymbol{\sigma }} \right){\mathit{\boldsymbol{H}}_{\rm{I}}}} \right) \in {{\bf{R}}^{3 \times 1}}, \end{array} $ | (9) |
| $ {\mathit{\boldsymbol{G}}^*}\left( {\mathit{\boldsymbol{\sigma }}, \mathit{\boldsymbol{\dot \sigma }}} \right) = - {\mathit{\boldsymbol{H}}^{* - 1}}{\mathit{\boldsymbol{G}}^{ - {\rm{T}}}}\mathit{\boldsymbol{Q}} \in {{\bf{R}}^{3 \times \left( {m + n} \right)}}, $ | (10) |
| $ \mathit{\boldsymbol{Q}} = \left[{{\mathit{\boldsymbol{A}}_{ct}}{\mathit{\boldsymbol{H}}_{cw}}, {\mathit{\boldsymbol{A}}_{ws}}{\mathit{\boldsymbol{I}}_{wws}}} \right] \in {{\bf{R}}^{3 \times \left( {m + n} \right)}}, $ | (11) |
| $ \boldsymbol{u}={{\left[{{{\boldsymbol{\dot{\gamma }}}}^{\text{T}}}, {{{\boldsymbol{\dot{\tilde{\omega }}}}}^{\text{T}}} \right]}^{\text{T}}}\in {{\mathbf{R}}^{\left( m+n \right)\times 1}}, $ | (12) |
| $ {\mathit{\boldsymbol{H}}^*}\left( \mathit{\boldsymbol{\sigma }} \right) = {\mathit{\boldsymbol{G}}^{ - {\rm{T}}}}\mathit{\boldsymbol{J}}{\mathit{\boldsymbol{G}}^{ - 1}} \in {{\bf{R}}^{3 \times 3}}. $ | (13) |
将式(8)改写成状态空间形式为
| $ \frac{{\rm{d}}}{{{\rm{d}}t}}\left[\begin{array}{l} \mathit{\boldsymbol{\sigma }}\\ {\mathit{\boldsymbol{\dot \sigma }}} \end{array} \right] = {\mathit{\boldsymbol{A}}_0}\left[\begin{array}{l} \mathit{\boldsymbol{\sigma }}\\ {\mathit{\boldsymbol{\dot \sigma }}} \end{array} \right] + {\mathit{\boldsymbol{B}}_0}\left( {{\mathit{\boldsymbol{F}}^*}\left( {\mathit{\boldsymbol{\sigma }}, \mathit{\boldsymbol{\dot \sigma }}} \right) + {\mathit{\boldsymbol{G}}^*}\left( {\mathit{\boldsymbol{\sigma }}, \mathit{\boldsymbol{\dot \sigma }}} \right)\mathit{\boldsymbol{u}}} \right), $ | (14) |
其中
| $ {\mathit{\boldsymbol{A}}_0}\left[{\begin{array}{*{20}{c}} {\bf{0}}&\mathit{\boldsymbol{I}}\\ {\bf{0}}&{\bf{0}} \end{array}} \right], {\mathit{\boldsymbol{B}}_0} = \left[\begin{array}{l} {\bf{0}}\\ \mathit{\boldsymbol{I}} \end{array} \right]. $ |
安装偏差以及卫星发射时振动所造成的结构偏差,会严重降低执行机构的控制精度. CMG群的力矩输出矩阵Act、飞轮群角动量矩阵Aws分别为
| $ {\mathit{\boldsymbol{A}}_{ct}} = \mathit{\boldsymbol{A}}_{ct}^n + \mathit{\boldsymbol{A}}_{ct}^\Delta, {\mathit{\boldsymbol{A}}_{ws}} = \mathit{\boldsymbol{A}}_{ws}^n + \mathit{\boldsymbol{A}}_{ws}^\Delta, $ |
式中,A*n、A*Δ分别表示相应的标称值以及标称值和准确值之间的偏差.整星角动量可以表示为
| $ {\mathit{\boldsymbol{H}}_{\rm{I}}} = \mathit{\boldsymbol{H}}_{\rm{I}}^n + \mathit{\boldsymbol{H}}_{\rm{I}}^\Delta, $ |
式中HIΔ、HIn分别表示角动量估计偏差值和标称值.则式(9)与式(10)可以写成
| $ {\mathit{\boldsymbol{F}}^*} = {\mathit{\boldsymbol{F}}^{*n}} + {\mathit{\boldsymbol{F}}^{*\Delta }}, {\mathit{\boldsymbol{G}}^*} = {\mathit{\boldsymbol{G}}^{*n}} + {\mathit{\boldsymbol{G}}^{*\Delta }}, $ |
其中:
| $ {\mathit{\boldsymbol{F}}^{*n}} = {\mathit{\boldsymbol{H}}^{* - 1}}\left( {{\mathit{\boldsymbol{G}}^{ - {\rm{T}}}}\mathit{\boldsymbol{J}}{\mathit{\boldsymbol{G}}^{ - 1}}\mathit{\boldsymbol{\dot G}}{\mathit{\boldsymbol{G}}^{ - 1}}\mathit{\boldsymbol{\dot \sigma }} - {\mathit{\boldsymbol{G}}^{ - {\rm{T}}}}{\mathit{\boldsymbol{\omega }}^ \times }\mathit{\boldsymbol{C}}\left( \mathit{\boldsymbol{\sigma }} \right)\mathit{\boldsymbol{H}}_{\rm{I}}^n} \right), $ | (15) |
| $ {\mathit{\boldsymbol{F}}^{*\Delta }} = - {\mathit{\boldsymbol{H}}^{* - 1}}{\mathit{\boldsymbol{G}}^{ - {\rm{T}}}}{\mathit{\boldsymbol{\omega }}^ \times }\mathit{\boldsymbol{C}}\left( \mathit{\boldsymbol{\sigma }} \right)\mathit{\boldsymbol{H}}_{\rm{I}}^\Delta, $ | (16) |
且
| $ {\mathit{\boldsymbol{G}}^{*n}} = - {\mathit{\boldsymbol{H}}^{* - 1}}{\mathit{\boldsymbol{G}}^{ - {\rm{T}}}}{\mathit{\boldsymbol{Q}}^n}, $ | (17) |
| $ {\mathit{\boldsymbol{G}}^{*\Delta }} = - {\mathit{\boldsymbol{H}}^{* - 1}}{\mathit{\boldsymbol{G}}^{ - {\rm{T}}}}{\mathit{\boldsymbol{Q}}^\Delta }, $ | (18) |
式中Qn、QΔ分别表示Q的标称值和估计偏差.
为便于后续自适应控制器的设计,式(16)可写成以下形式:
| $ {\mathit{\boldsymbol{F}}^{*\Delta }} = {\mathit{\boldsymbol{Y}}_F}{\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}_F}. $ |
式中:ΘF=HIΔ为待估计的角动量参数,YF=-H*-1G-Tω×C(σ)是关于σ和
同样,式(18)也可以写成:
| $ \begin{array}{l} {\mathit{\boldsymbol{G}}^{*\Delta }} = - {\mathit{\boldsymbol{H}}^{* - 1}}{\mathit{\boldsymbol{G}}^{ - {\rm{T}}}}\left[{\mathit{\boldsymbol{A}}_{ct}^\Delta {\mathit{\boldsymbol{H}}_{cw}}, \mathit{\boldsymbol{A}}_{ws}^\Delta {\mathit{\boldsymbol{I}}_{wws}}} \right], \\ \mathit{\boldsymbol{A}}_{ct}^\Delta {\mathit{\boldsymbol{H}}_{cw}} = \left[{\mathit{\boldsymbol{t}}_{c1}^\Delta, \mathit{\boldsymbol{t}}_{c2}^\Delta, \cdots, \mathit{\boldsymbol{t}}_{cN}^\Delta } \right]{\rm{diag}}\left( {{h_{cwi}}} \right) = \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\left[{\mathit{\boldsymbol{t}}_{c1}^\Delta {h_{cw1}}, \cdots, \mathit{\boldsymbol{t}}_{ci}^\Delta {h_{cwi}}, \cdots, \mathit{\boldsymbol{t}}_{cN}^\Delta {h_{cwN}}} \right], \end{array} $ |
其中
| $ \mathit{\boldsymbol{t}}_{ci}^\Delta {h_{cwi}} = \left( {\mathit{\boldsymbol{t}}_{c0}^\Delta \cos {\mathit{\boldsymbol{\gamma }}_i} - \mathit{\boldsymbol{s}}_{c0}^\Delta \sin {\mathit{\boldsymbol{\gamma }}_i}} \right){h_{cwi}}. $ |
式中tci0Δ、sci0Δ分别表示在CMG框架角均为0时的力矩输出和转子轴方向偏差.
设
| $ {\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}_{cGi}} = {\left[{\mathit{\boldsymbol{t}}_{ci0}^{\Delta {\rm{T}}}, \mathit{\boldsymbol{s}}_{ci0}^{\Delta {\rm{T}}}} \right]^{\rm{T}}} \in {{\bf{R}}^6}, $ |
则
| $ {\mathit{\boldsymbol{Y}}_{cGi}} = - {h_{wci}}{\mathit{\boldsymbol{H}}^{{*^{ - 1}}}}{\mathit{\boldsymbol{G}}^{ - {\rm{T}}}}\left[{\cos {\mathit{\boldsymbol{\gamma }}_i}{\mathit{\boldsymbol{I}}_3}, -\sin {\mathit{\boldsymbol{\gamma }}_i}{\mathit{\boldsymbol{I}}_3}} \right] \in {{\bf{R}}^{3 \times 6}}, $ |
于是可以得到
| $ \begin{array}{l} {\mathit{\boldsymbol{Y}}_{cG}} = \left[{{\mathit{\boldsymbol{Y}}_{cG1}}, {\mathit{\boldsymbol{Y}}_{cG2}}, \cdots, {\mathit{\boldsymbol{Y}}_{cGm}}} \right] \in {{\bf{R}}^{3 \times 6m}}, \\ {\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}_{cG}} = {\rm{diag}}\left( {{\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}_{cG1}}, {\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}_{cG2}}, \cdots, {\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}_{cGm}}} \right) \in {{\bf{R}}^{6m \times m}}. \end{array} $ | (19) |
同理
| $ \begin{array}{l} \mathit{\boldsymbol{A}}_{ws}^\Delta {\mathit{\boldsymbol{I}}_{wws}} = \left[{{\mathit{\boldsymbol{I}}_{wws1}}{\mathit{\boldsymbol{I}}_3}, {\mathit{\boldsymbol{I}}_{wws2}}{\mathit{\boldsymbol{I}}_3}, \cdots, {\mathit{\boldsymbol{I}}_{wwsN}}{\mathit{\boldsymbol{I}}_3}} \right].\\ \;\;\;\;\;\;\;\;\;\;\;\;\;{\rm{diag}}\left( {\mathit{\boldsymbol{s}}_{w1}^\Delta, \mathit{\boldsymbol{s}}_{w2}^\Delta, \cdots, \mathit{\boldsymbol{s}}_{wN}^\Delta } \right), \end{array} $ |
于是可以得到
| $ \begin{array}{l} {\mathit{\boldsymbol{Y}}_{wG}} = - {\mathit{\boldsymbol{H}}^{* - 1}}{\mathit{\boldsymbol{G}}^{ - {\rm{T}}}}\left[{{\mathit{\boldsymbol{I}}_{wws1}}{\mathit{\boldsymbol{I}}_3}, {\mathit{\boldsymbol{I}}_{wws2}}{\mathit{\boldsymbol{I}}_3}, \cdots, {\mathit{\boldsymbol{I}}_{wwsN}}{\mathit{\boldsymbol{I}}_3}} \right] \in {{\bf{R}}^{3 \times 3n}}, \\ {\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}_{wG}} = \;{\rm{diag}}\left( {\mathit{\boldsymbol{s}}_{w1}^\Delta, \mathit{\boldsymbol{s}}_{w2}^\Delta, \cdots, \mathit{\boldsymbol{s}}_{wN}^\Delta } \right) \in {{\bf{R}}^{3 \times 3n}}. \end{array} $ | (20) |
将式(19)与式(20)合并可以写为
| $ \begin{array}{l} {\mathit{\boldsymbol{Y}}_G} = \left[{{\mathit{\boldsymbol{Y}}_{cG}}, {\mathit{\boldsymbol{Y}}_{wG}}} \right] \in {{\bf{R}}^{3 \times 3n\left( {2m + n} \right)}}, \\ \;\;\;\;\;\;\;{\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}_G} = \left[{\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}_{cG}}}&{}\\ {}&{{\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}_{wG}}} \end{array}} \right], \end{array} $ |
则式(18)可写成如下简洁形式:
| $ {\mathit{\boldsymbol{G}}^{*\Delta }} = {\mathit{\boldsymbol{Y}}_G}{\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}_G}. $ |
完成控制模型的建立,本文在此基础上进行控制器设计.
3 自适应控制律设计使用σd(t)表示相对于惯性系卫星的参考姿态,假设σd(t)及其导数项
| $ \mathit{\boldsymbol{e}} \buildrel \Delta \over = \left[\begin{array}{l} {\mathit{\boldsymbol{\sigma }}_e}\\ {{\mathit{\boldsymbol{\dot \sigma }}}_e} \end{array} \right] = \left[\begin{array}{l} \mathit{\boldsymbol{\sigma }}-{\mathit{\boldsymbol{\sigma }}_d}\\ \mathit{\boldsymbol{\dot \sigma }}-{{\mathit{\boldsymbol{\dot \sigma }}}_d} \end{array} \right]. $ |
根据式(14),可以得到卫星的跟踪误差动力学为
| $ \begin{array}{l} \frac{{\rm{d}}}{{{\rm{d}}t}}\mathit{\boldsymbol{e = }}\frac{{\rm{d}}}{{{\rm{d}}t}}\left[\begin{array}{l} \mathit{\boldsymbol{\sigma }}-{\mathit{\boldsymbol{\sigma }}_d}\\ \mathit{\boldsymbol{\dot \sigma }}-{{\mathit{\boldsymbol{\dot \sigma }}}_d} \end{array} \right] = {\mathit{\boldsymbol{A}}_0}\mathit{\boldsymbol{e}} + {\mathit{\boldsymbol{B}}_0}\left( {{\mathit{\boldsymbol{F}}^*}\left( {\mathit{\boldsymbol{\sigma }}, \mathit{\boldsymbol{\dot \sigma }}} \right) + } \right.\\ \;\;\;\;\;\;\;\;\left. {{\mathit{\boldsymbol{G}}^*}\left( {\mathit{\boldsymbol{\sigma }}, \mathit{\boldsymbol{\dot \sigma }}} \right)\mathit{\boldsymbol{u}} - {{\mathit{\boldsymbol{\ddot \sigma }}}_{\rm{d}}}} \right), \end{array} $ | (21) |
系统(A0,B0)可控,则可通过选取合适的矩阵K使得矩阵A1=A0-B0K满足Hurwitz矩阵的条件,式(21)可改写成
| $ \begin{array}{l} \mathit{\boldsymbol{\dot e}} = {\mathit{\boldsymbol{A}}_1}\mathit{\boldsymbol{e}} + {\mathit{\boldsymbol{B}}_0}\left( {\mathit{\boldsymbol{Ke}} + {\mathit{\boldsymbol{F}}^*}} \right.\left( {\mathit{\boldsymbol{\sigma }}, \mathit{\boldsymbol{\dot \sigma }}} \right) + \\ \;\;\;\;\left. {{\mathit{\boldsymbol{G}}^*}\left( {\mathit{\boldsymbol{\sigma }}, \mathit{\boldsymbol{\dot \sigma }}} \right)\mathit{\boldsymbol{u}} - {{\mathit{\boldsymbol{\ddot \sigma }}}_d}} \right). \end{array} $ | (22) |
选择系统Lyapunov函数,如
| $ \mathit{V} = \frac{1}{2}{\mathit{\boldsymbol{e}}^{\rm{T}}}\mathit{\boldsymbol{Pe}} + \frac{1}{{2{\alpha _F}}}\mathit{\mathit{\pmb{\tilde \Theta }}}_F^{\rm{T}}{{\mathit{\mathit{\pmb{\tilde \Theta }}}}_F} + \frac{1}{{2{\alpha _G}}}{\rm{tr}}\mathit{\mathit{\pmb{\tilde \Theta }}}_G^{\rm{T}}{{\mathit{\mathit{\pmb{\tilde \Theta }}}}_G}. $ | (23) |
式中:
设计反馈控制器u, 如
| $ \boldsymbol{u}={{\left( {{\boldsymbol{G}}^{*n}}+{{\boldsymbol{Y}}_{G}}{{{\mathit{\pmb{\hat{\Theta }}}}}_{G}} \right)}^{\dagger }}\left( - \boldsymbol{Ke}-{{\boldsymbol{F}}^{*n}}-{{\boldsymbol{Y}}_{F}}{{{\mathit{\pmb{\hat{\Theta }}}}}_{F}}+{{{\boldsymbol{\ddot{\sigma }}}}_{d}} \right), $ | (24) |
可以消除系统中其他非线性项,其中
将控制器(24)代入式(22)可得
| $ \begin{array}{l} \boldsymbol{\dot e} = {\boldsymbol{A}_1}\boldsymbol{e} + {\boldsymbol{B}_0}\left( {\boldsymbol{Ke} + {\boldsymbol{F}^{*n}} + {\boldsymbol{Y}_F}{\mathit{\pmb{\Theta}} _F} + } \right.\\ \;\;\;\;\;\left. {\left( {{\boldsymbol{G}^{*n}} + {\boldsymbol{Y}_G}{\mathit{\pmb{{\tilde \Theta }}}_G} + {\boldsymbol{Y}_G}{\mathit{\pmb{{\hat \Theta }}}_G}} \right)\boldsymbol{u} - {{\ddot \sigma }_d}} \right) = \\ \;\;\;\;\;{\boldsymbol{A}_1}\boldsymbol{e} + {\boldsymbol{B}_0}{\boldsymbol{Y}_F}{{\mathit{\pmb{\tilde \Theta }}}_F} + {\boldsymbol{B}_0}{\boldsymbol{Y}_G}{\mathit{\pmb{{\tilde \Theta }}}_G}\boldsymbol{u}. \end{array} $ |
此时,式(23)的导数形式为
| $ \begin{align} & \dot{V}=-\frac{1}{2}{{\boldsymbol{e}}^{\text{T}}}\boldsymbol{Qe}+\frac{1}{{{\alpha }_{F}}}\left( {{\alpha }_{F}}{{\boldsymbol{e}}^{\text{T}}}\boldsymbol{P}{{\boldsymbol{B}}_{0}}{{\boldsymbol{Y}}_{F}}-\mathit{\pmb{\dot{\hat{\Theta }}}}_{F}^{\text{T}} \right){{{\mathit{\pmb{\tilde{\Theta }}}}}_{F}}+ \\ & \ \ \ \ \ \frac{1}{{{\alpha }_{G}}}\sum\limits_{i=1}^{m+n}{\left( {{\alpha }_{G}}{{\boldsymbol{e}}^{\text{T}}}\boldsymbol{P}{{\boldsymbol{B}}_{0}}{{\boldsymbol{Y}}_{Gi}}{{\boldsymbol{u}}_{i}}-\mathit{\pmb{\dot{\hat{\Theta }}}}_{Gi}^{\text{T}} \right)}{{{\mathit{\pmb{\tilde{\Theta }}}}}_{Gi}}. \\ \end{align} $ |
选择其中参数更新方式为
| $ {{{\mathit{\pmb{\dot{\hat{\Theta }}}}}}_{F}}={{\alpha }_{F}}\boldsymbol{Y}_{F}^{\text{T}}\boldsymbol{B}_{0}^{\text{T}}\boldsymbol{Pe}, $ | (25) |
| $ {{{\mathit{\pmb{\dot{\hat{\Theta }}}}}}_{Gi}}={{\alpha }_{G}}\boldsymbol{Y}_{Gi}^{\text{T}}\boldsymbol{B}_{0}^{\text{T}}\boldsymbol{P}{{\boldsymbol{e}}^{\text{T}}}{{u}_{i}}, $ | (26) |
可以使得Lyapunov函数的导数满足以下条件:
| $ \dot V = - \frac{1}{2}{\mathit{\boldsymbol{e}}^{\rm{T}}}\mathit{\boldsymbol{Qe}} \le 0. $ |
从上述推导和分析可以得出,控制器(24)以及参数更新率(25)与(26)能够使得系统跟踪误差收敛.在控制器(24)实际执行过程中,需要避免因为
| $ {{\mathit{\pmb{\dot \Theta }}}_{\mathit{Gi}}}\mathit{ = Proj}\left( {{{\mathit{\pmb{\hat \Theta }}}_{\mathit{Gi}}}\mathit{, }{\mathit{\pmb{\Phi }}_{\mathit{Gi}}}} \right)\mathit{, } $ |
其中
| $ {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{\mathit{Gi}}} \buildrel \Delta \over = \mathit{\boldsymbol{T}}_{Gi}^{\rm{T}}\mathit{\boldsymbol{B}}_0^{\rm{T}}\mathit{\boldsymbol{P}}{\mathit{\boldsymbol{e}}^{\rm{T}}}{u_i} \in {{\bf{R}}^6} $ |
Proj(
1)如果
| $ {\rm{Proj}}\left( {{{\mathit{\pmb{\hat \Theta }}}_{\mathit{Gi}}}\mathit{, }{\mathit{\pmb{\Phi }}_{\mathit{Gi}}}} \right)\mathit{ = }{\mathit{\alpha }_\mathit{G}}{\mathit{\pmb{\Phi }}_{\mathit{Gi}}}\mathit{.} $ |
2)如果
| $ {\rm{Proj}}\left( {{{\mathit{\pmb{\hat \Theta }}}_{\mathit{Gi}}}\mathit{, }{\mathit{\pmb{\Phi }}_{\mathit{Gi}}}} \right)\mathit{ = }{\mathit{\alpha }_\mathit{G}}\left( {{\mathit{\pmb{\Phi }}_{\mathit{Gi}}}\mathit{ - }\frac{{\left( {{{\left\| {{\mathit{\pmb{\Phi }}_{\mathit{Gi}}}} \right\|}^\mathit{2}}\mathit{ - }{\mathit{\beta }_{\mathit{Gi}}}} \right)\mathit{\pmb{\Phi }}_{\mathit{Gi}}^\mathit{T}{{\mathit{\pmb{\hat \Theta }}}_{\mathit{Gi}}}}}{{{\mathit{\delta }_{\mathit{Gi}}}{{\left\| {{{\mathit{\pmb{\hat \Theta }}}_{\mathit{Gi}}}} \right\|}^\mathit{2}}}}{{\mathit{\pmb{\hat \Theta }}}_{\mathit{Gi}}}} \right)\mathit{.} $ |
式中βGi是已知正的常值.
4 结果及分析对上述的控制器进行数学仿真,以验证其有效性.卫星携带CMG和飞轮作为执行机构.其中4个CMG采用金字塔构型安装, 3个正装飞轮,而实际安装矩阵在标称安装矩阵加最大±0.05的随机偏差.
为测试控制算法对参考轨迹的跟踪能力,选择式(27)的正弦曲线作为卫星的姿态角速度参考轨迹,初始姿态四元数为[1, 0, 0, 0].
| $ \begin{array}{l} {\omega _f} = 0.02 \times \left( {\sin \left( {2{\rm{\pi }}t/800} \right)} \right., \\ {\left. {\sin \left( {2{\rm{\pi }}t/600} \right), \sin \left( {2{\rm{\pi }}t/400} \right)} \right)^{\rm{T}}}{\rm{rad/s}}{\rm{.}} \end{array} $ | (27) |
选取合适的K,使得式(24)中矩阵A1=A0-B0K的特征值为(保证控制算法具有好的收敛性能)
| $ \begin{array}{l} \mathit{\boldsymbol{Q}} = {\mathit{\boldsymbol{I}}_6}, {\alpha _F} = 1.0 \times {10^7}, {\alpha _G} = 1.0 \times {10^3}, \\ \;\;\;\;\;\;\;\;\;\;\;\;\;{\delta _{Gi}} = 0.1, {\beta _{Gi}} = 0.05. \end{array} $ |
仿真效果对比,首先给出不使用自适应控制律的控制结果,即令αF=αG=0,仿真结果如图 2,3所示.从仿真结果可以看出,欧拉角与角速度跟踪误差分别在0.3 rad和10-3rad/s量级.
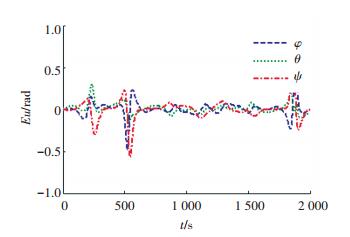
|
图 2 欧拉角表示的无自适应控制时姿态跟踪误差 Figure 2 The attitude tracking error represented by Euler angle without the adaptive control |
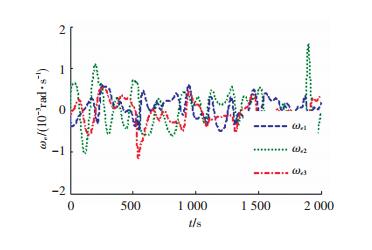
|
图 3 无自适应控制时角速度跟踪误差 Figure 3 The angular velocity tracking error without the adaptive control |
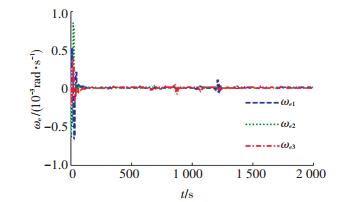
采用本文所设计的自适应控制算法,仿真结果如图 4~11所示.从图 4可以看出,欧拉角跟踪误差迅速达到并稳定在0.003 rad.图 5的角速度跟踪误差曲线也呈现同样的趋势,其控制精度稳定时可达到10-4rad/s量级.
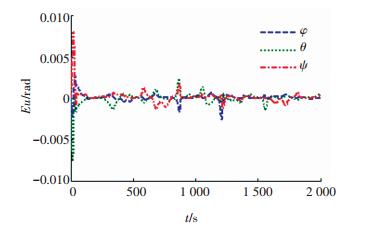
|
图 4 欧拉角表示的姿态跟踪误差 Figure 4 The attitude tracking error represented by Euler angle |
|
图 5 角速度跟踪误差 Figure 5 The angular velocity tracking error |

|
图 6 CMG的框架角 Figure 6 The gimbal angles of CMG |
|
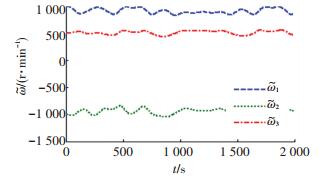
图 7 飞轮转速 Figure 7 The angular rate of flywheels |
卫星角动量的估计情况如图 8, 9所示,自适应控制律使得系统很快趋近于真实的系统角动量(在图 9使用直线表示).

|
图 8 ΘF的参数估计 Figure 8 The estimated value for ΘF |

|
图 9 卫星整体角动量的估计 Figure 9 The estimated value for the angular momentum of the satellite |
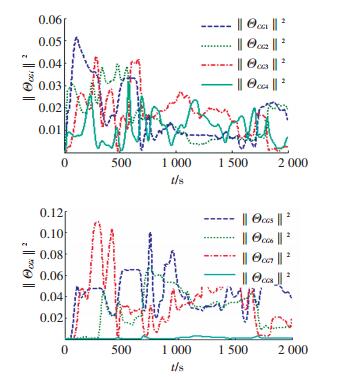
从图 10, 11的ΘcG和ΘwG的模的平方曲线可以看出,在平滑映射的作用下,
|
图 10 ΘcG的参数估计的范数 Figure 10 The norm of the estimated value for ΘcG |

|
图 11 ΘwG的参数估计的范数 Figure 11 The norm of the estimated value for ΘwG |
1)从跟踪正弦形式的姿态角速度参考轨迹的结果,本文设计的自适应控制器能够提高2个数量级的姿态控制精度,以及1个数量级的姿态角速度控制精度.
2)基于平滑映射原理所设计自适应参数更新律保证参数估计结果的同时,也保证自适应参数更新不会出现奇异现象.
| [1] |
刘刚, 李传江, 马广富, 等. 应用SGCMG的卫星姿态快速机动控制[J].
航空学报,2011, 32 (10) : 1-9.
LIU Gang, LI Chuanjiang, MA Guangfu, et al. Time efficient controller design for satellite attitude maneuvers using SGCMG[J]. Acta Aeronautica ET Astronautica Sinica,2011, 32 (10) : 1-9. |
| [2] | LONGBOTHAMN, BLEILER C, CHAAPEL C, et al. Spectral classification of worldview-2 multi-angle sequence[C]//IEEE GRSS and ISPRS Joint Urban Remote Sensing Event. Munich, Germany: IEEE Computer Society, 2011: 109-112. DOI: 10.1109/JURSE.2011.5764731. |
| [3] | GIROUARTB, SEBBAG I, LACHIVER J M. Pleiades-HR CMGs-based attitude control system design, development status and performances[C]//Proceedings of 17th IFAC Symposium on Automatic Control in Aerospace. Toulouse, France: 2007: 834-839. DOI:10.3182/20070625-5-FR-2916.00142. |
| [4] |
叶东, 屠园园, 孙兆伟. 面向非沿轨迹成像卫星的切比雪夫神经网络滑模姿态控制[J].
航空学报,2015, 36 (9) : 3092-3104.
E Dong, TU Yuanyuan, SUN Zhaowei. Sliding mode control for nonparallel-ground-track imaging using Chebyshev neural network[J]. Acta Aeronautica ET Astronautica Sinica,2015, 36 (9) : 3092-3104. |
| [5] | WIE Bong. Singularity escape/avoidance steering logic for control moment gyro systems[J]. Journal of Guidance Control and Dynamics,2005, 28 (5) : 948-956. DOI: 10.2514/1.10136 |
| [6] | LAPPAS V J. A Control moment gyro (CMG) based attitude control system (ACS) for agile small satellites[D]. England: University of Surrey, 2002: 1-9. |
| [7] | CHEN Xiaojiang, STEYN W H. Robust combined eigenaxis slew manoeuvre[C]. AIAA Guidance, Navigation, and Control Conference. 1999: 521-529. |
| [8] | SUN Zhaowei, GENG Yunhai, XU Guodong, et al. The combined control algorithm for large-angle maneuver of hitsat-1 small satellite[J]. Acta Astronautica,2004, 54 (7) : 463-469. DOI: 10.1016/S0094-5765(03)00223-6 |
| [9] | HALLC D, TSIOTRAS P, SHEN Haijun. Tracking rigid body motion using thrusters and momentum wheels[J]. Journal of the Astronautical Sciences,2002, 50 (3) : 311-323. DOI: 10.2514/6.1998-4471 |
| [10] |
叶东, 孙兆伟, 王剑颖. 敏捷卫星的联合执行机构控制策略[J].
航空学报,2012, 33 (6) : 1108-1115.
YE Dong, SUN Zhaowei, WANG Jianying. Control strategy of hybrid actuator for agile satellites[J]. Acta Aeronautica ET Astronautica Sinica,2012, 33 (6) : 1108-1115. |
| [11] | FORDK A, Hall C D. Singular direction avoidance steering for control-moment gyros[J]. Journal of Guidance Control and Dynamics,2000, 23 (4) : 648-656. DOI: 10.2514/2.4610 |
| [12] | LEVEF A, FITZCOY N G. Hybrid steering logic for single-gimbal control moment gyroscopes[J]. Journal of Guidance Control and Dynamics,2010, 33 (4) : 1202-1212. DOI: 10.2514/1.46853 |
| [13] | STEVENSON D, SCHAUB H. Nonlinear control analysis of a double-gimbal variable-speed control Moment gyroscope[J]. Journal of Guidance Control and Dynamics,2012, 35 (3) : 787-793. DOI: 10.2514/1.56104 |
| [14] | LIDEN S. A new fail operational control moment gyro configuration[C]. Guidance, Control and Flight Mechanics Conference. American Institute of Aeronautics and Astronautics, 1971: 1-9. DOI: 10.2514/6.1971-936. |
| [15] | ROITHMAYRC M, KARLGAAR C D, KUMAR R R, et al. Dynamics and control of attitude, power, and momentum for a spacecraft using flywheels and control moment gyroscopes[R]. Hampton, VA: National Aeronautics and Space Administration, 2003: 1-91. |
| [16] | SKELTONC E, HALL C. Mixed control moment gyro and momentum wheel attitude control strategies[J]. Astrodynamics,2003, 116 (1) : 887-899. |
| [17] | RIZVI F. Cassini thruster calibration algorithm using reaction wheel biasing data[J]. Journal of Spacecraft and Rockets,2014, 51 (2) : 563-573. DOI: 10.2514/1.A32523 |
| [18] | CHANGY C. An adaptive H∞ tracking control for a class of nonlinear multiple-input multiple-output (MIMO) systems[J]. IEEE Transactions on Automatic Control,2001, 46 (9) : 1432-1437. DOI: 10.1109/9.948472 |
 2016, Vol. 48
2016, Vol. 48


