随着软件产业的迅速发展及软件系统的日益庞大和复杂,每一个软件系统往往会涉及多个雇主甚至大量的雇主,每个雇主对于系统的功能特征、性能特征、UI特征、业务流程都有自己的理解,往往会产生大量的软件需求,但是由于受到开发成本和开发时间的限制,每一个软件系统都无法同时满足所有雇主的需求[1].雇主往往会由于现实生活中的工作职能不同,对需求集合的优化选择具有不同的期望,对需求的优先实现顺序持有不同的意见,这些意见甚至可能是彼此冲突的[2].如何从庞大的需求集合中优选出一个子集,既要尽可能高地保证不同雇主的满意度,又要确保有足够的资源来实现选定的需求,成为需求工程中一个具有挑战性的问题.
需求优选的过程需要同时兼顾多个目标,所以在数学上多雇主需求优选问题可以形式化为一个多目标优化问题.非支配排序遗传算法Ⅱ(Non-dominated Sorted Genetic Algorithm-Ⅱ,NSGA-Ⅱ)是解决多目标优选问题的经典方法[3],然而传统的NSGA-Ⅱ算法存在着精英解易丢失等问题[4].因此,本文在传统的NSGA-Ⅱ算法基础上采用基于存档的NSGA-Ⅱ算法,将其应用于多雇主的需求优选中,通过将每一次迭代过程中产生的非支配解保存至文档的方式,既保持了传统NSGA-Ⅱ算法能够保留优良解集、降低计算复杂度的优势,又克服了NSGA-Ⅱ算法精英解丢失的不足.在大规模仿真数据集上的实验结果表明,本文方法均优于基线方法.
1 多雇主需求优选的研究现状平衡不同雇主之间的不同期望、平衡系统和雇主需求之间的矛盾,是需求优选过程中无法回避的难题,通常需要采用基于搜索的寻优算法来探索和解决这类复杂的优选问题.基于搜索的需求优选技术,就是要将问题塑造成基于搜索的优化问题,在适应度函数的指导下,寻找最优或近似最优的解决方案[5].研究人员认识到了基于搜索的软件工程(SBSE)方法在贯穿整个软件工程领域的各个问题中的巨大应用价值,单目标和多目标优化方法被广泛的应用到需求优选问题中[6-7].
1.1 多目标优化问题的定义多目标优化问题就是存在多个目标需要同时优化的问题,由于目标间是没有办法进行比较的,又可能存在冲突,所以可能不存在使所有目标函数同时达到最优的解.一个解可能对某个目标函数来说是最差的解,但是对另外的目标问题却是最好的解,因此求解多目标优化问题的最优解十分困难,它通常不是一个单一的解,而是一个集合,这个集合定义为非劣最优解集,或帕累托(Pareto)最优解集[8].多目标优化问题的形式化定义为
| $ \begin{array}{l} max/min\left( {{f_1}\left( x \right), {f_2}\left( x \right), \cdots, {f_n}\left( x \right)} \right), \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\rm{s}}{\rm{.t}}{\rm{.}}g\left( x \right). \end{array} $ |
式中:f(x)为目标函数,g(x)为约束条件. Pareto最优解集中的每个解对所有的目标函数来说是没有好坏之分的,Pareto最优解的特征是:没有办法再进行改进,若改进一个目标函数,则必然会减弱另外一个目标函数.因此,Pareto最优解集中的每一个解,都是多目标优化问题的一个非劣解,在这个解集中,根据不同目标的权重或其他信息进行选择,可以得到满意解.
Srinivas和Deb在1995年,基于Pareto最优概念,将非支配排序遗传算法NSGA运用于多目标优化[9],在基本遗传算法的基础上,对选择再生方法进行改进,将每个个体按照它们的支配与非支配关系进行分层,再做选择操作,从而使得算法在多目标优化方面得到非常满意的结果.
1.2 基于多目标优化的需求优选技术随着系统复杂度的提高,单个目标的优化不能充分满足所有目标的利益,无法满足多个雇主的期望. Finkelstein等[10]的研究表明多目标优化技术可应用于解决需求分配的公平性,他们将不同定义的公平性作为不同的优化目标,利用多目标优化技术来同时优化不同的公平性目标. Zhang等[11]同时考虑最小化供应商的成本和最大化雇主满意度的双重目标. Saliu等[12]同时考虑了实施和需求这两个层面的优化目标,依据商业需求满足和实施效益两个角度,来优化软件的发布计划. Zhang等[13]2007年首次将NRP问题概括为多目标NRP(Multi-Object Next Release Problem, MONRP)问题,提出了基于多目标优化的NRP问题模型,将“成本”限制和“价值”追求作为两个独立的目标进行优化,来平衡和优化价值和成本之间的矛盾. Zhang等[11]提出将每个雇主的满意度作为单独的优化目标,将基于非支配遗传算法(NSGA)的改进算法NSGA-Ⅱ算法应用到了需求优选的问题中.此外,一些多目标进化算法及杂合算法也被应用来解决MONRP问题[14-17].
尽管现有的基于搜索的需求优选方法为优选问题提供了很好的解决方案,能够自动搜索最优或近似最优的需求集合来平衡相互竞争的多个雇主,然而基于多目标优化的需求优选方法对无约束或简单约束的优化问题可以找到很好的解决方案,但当解决高约束问题,或者优化目标急剧增多时,会导致效率大幅降低,无法达到理想的优选效果.在所有应用于需求优选的SBSE搜索方法中,NSGA-Ⅱ算法是最常用的方法[18].一些研究人员认为NSGA-Ⅱ是求解大规模复杂的多目标优化问题的最快、最有效的算法[13, 19].然而传统的NSGA-Ⅱ算法存在着精英解易丢失等问题[4].本文将在前人研究的基础之上,提出基于存档NSGA-Ⅱ算法的多雇主需求优选方法.针对以往多目标优化方法计算复杂度高、搜索效率低的弊病,通过引入NSGA-Ⅱ算法降低了多雇主优化目标带来的高计算复杂度,并通过文档记录每一次迭代的非支配性解集的方式,大幅度减少精英解集在迭代过程中的流失,取得了较好的需求优选效果.
2 基于存档NSGA-Ⅱ算法的多雇主需求优选方法 2.1 多雇主需求优选问题的形式化描述令S={S1, S2, …, SM}表示包含M个雇主的集合,R={R1, R2, …, Rn}表示包含n个需求的集合,C={cost1, cost2, …, costn}表示实现每个需求所需要的代价,costi为实现Ri所需要的代价.雇主Si对需求Ri的打分记为v(Ri, Si),v(Ri, Si)=0表示雇主Si不期望实现需求Ri,v(Ri, Si)>0表示雇主Si期望实现需求Ri,v的取值越大,表示雇主越希望实现该需求.定义决策向量x=[x1, x2, …, xn],xi∈{0,1}表示雇主对于集合R中需求的选取情况,xi=1表示需求Ri被选取,xi=0表示需求Ri未被选取.
M个雇主对应了M个满意度,其中第j个雇主对应的满意度计算函数fj(x)为
| $ {f_j}\left( x \right) = \frac{{\sum\nolimits_{i = 1}^n {v\left( {{R_i}, {S_j}} \right)} \times {x_i}}}{{\sum\nolimits_{i = 1}^n {v\left( {{R_i}, {S_j}} \right)} }}. $ |
式中:xi表示第j个雇主对第i个需求选择的决策分量,v(Ri, Sj)表示第j个雇主对第i个需求的打分.对于任一决策变量x,实现需求的代价函数为
| $ cost\left( x \right) = \sum\nolimits_{i = 1}^n {cos{t_i}} \times {x_i}. $ |
多雇主的需求优选问题可以看成一个多目标优化问题,将雇主的满意度f1(x), f2(x), …, fM(x)作为优化目标,需求的实现代价cost(x)作为约束条件,B为代价阈值,即所能提供的最大需求实现代价,优化的目的就是在代价不超过B的基础上,最大限度地使M个目标函数达到最优,求解出尽可能使所有雇主满意度最大的需求决策向量x,即
| $ \begin{array}{l} max\left( {{f_1}\left( x \right), {f_2}\left( x \right), \cdots, {f_M}\left( x \right)} \right), \\ \;\;\;\;\;\;\;\;\;\;{\rm{s}}{\rm{.t}}{\rm{.cost}}\left( x \right) \le B. \end{array} $ |
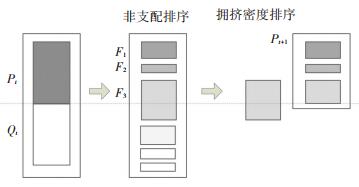
遗传算法将要解决的问题模拟成一个生物进化的过程,通过复制、交叉、突变等操作产生下一代的解,并逐步淘汰掉适应度函数值低的解,增加适应度函数值高的解,进化多代后就很有可能会进化出适应度函数值很高的个体.但在进化的过程中,由于交叉和突变操作的存在,精英解可能会丢失. NSGA-Ⅱ算法将最后一次迭代产生的种群作为非支配解集,虽然在进化过程中采用了精英策略,但还是会导致精英解的丢失.针对NSGA-Ⅱ算法可能会导致精英解丢失的问题,提出了基于存档的NSGA-Ⅱ算法,通过将每一次迭代过程中产生的非支配解保存至文档,来达到保留精英解的目的.基于存档的NSGA-Ⅱ算法原理图如图 1所示.

|
图 1 基于存档的NSGA-Ⅱ算法原理图 Figure 1 The flow chart for the archived NSGA-Ⅱ algorithm |
算法的具体执行步骤如下(见算法1):
1)获取参数信息,包括种群规模N、迭代次数T、交叉率、变异率,然后根据种群规模,随机生成一定数量的个体,即决策向量x,设初始种群为P0.
2)计算种群中个体的代价,即根据代价计算函数cost(x)计算个体的代价,并判断是否超过代价阈值B,若超过阈值,则随机生成新的个体替换该个体,若不超过阈值,则继续执行.
3)根据雇主对需求的打分,计算种群中所有个体对不同雇主的满意度,即传统遗传算法中的适应度值.
4)根据每个个体的适应度值,对个体进行快速非支配排序并根据个体间的支配关系进行分层.计算支配关系算法如算法2所示,根据个体间的支配关系,令np表示在种群中支配个体p的所有个体的数量,Sp表示被个体p支配的所有个体的集合.根据个体间支配关系进行分层时首先将np=0的个体加入第一层F1,对Sp集合中包含的所有个体q,将其nq的值减1,然后在剩余个体中取nq为0的个体加入第二层F2,直到所有个体都分层为止(详见算法3).
5)将进行快速非支配排序后得到的非支配解写入文档中.
6)从种群中选择N/2个个体得到FP,选择操作执行过程如图 2所示.
|
图 2 选择操作执行过程 Figure 2 The procedure for selection |
从第一层F1开始选择个体,若第一层数目小于N/2则继续选择第二层、第三层,直到个体数目到达N/2为止,若当前层中的个体数加上已选择的个体数之和大于N/2,则需要对当前层次中的个体进行拥挤密度排序,优先选择拥挤密度较小的个体,这样有利于保证种群的多样性.拥挤密度即在种群中给定点的周围个体的密度.对于包含两个目标的多目标优化问题,其拥挤密度示意图如图 3所示.个体i的拥挤密度通过计算其与相邻的个体i-1与个体i+1的距离得到,拥挤距离越大,则拥挤密度越小.

|
图 3 包含两个目标的多目标优化问题拥挤密度示意图 Figure 3 Crowding density for the bi-objective optimization |
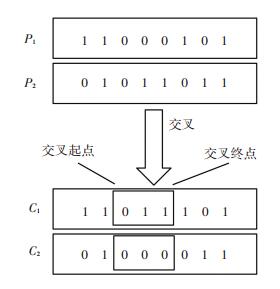
7)交叉.由于个体采用0,1编码串的方式表示,每个0或1都对应了一个需求的选取情况.根据初始时设置的交叉率,计算得出需要进行交叉的个体数量,每次交叉从FP中随机选择两个个体P1、P2,根据编码长度,产生两个随机位置作为交叉起点与终点,将起点与终点间的编码进行交换,形成两个新的个体C1和C2,交叉操作完成后得到种群FQ,交叉操作示意图如图 4所示.
|
图 4 对个体进行交叉操作示意图 Figure 4 The procedure for crossover |
8)变异.由于个体采用二进制编码即0,1串来表示需求的选取情况,因此根据变异率,从种群FQ中随机选择一定数量的个体,在编码长度范围内,随机选择一个位置,将此处的编码取反,即0变为1,1变为0,从而得到新的种群FQ.
9)将复制得到的来自父代的FP与由交叉突变操作新产生的FQ合并形成包含N个个体的子代种群Pt+1,重新执行步骤2)至步骤8),直到迭代次数超过阈值,迭代终止.
10)对文档中的个体按照步骤4)进行非支配排序与分层,仅保留分层结果的第一层,即不受任何其他个体支配的个体的集合,这个集合即为通过基于存档NSGA-Ⅱ算法得到的最优解集.
算法1 基于归档的NSGA-Ⅱ算法主循环
输入:种群规模N、迭代次数T、代价阈值B、交叉率、变异率、初始种群P0
输出:需求优选的解集
while t < =T do
for 种群Pt中的每一个个体x do
计算个体的代价cost(x)
if cost(x)>B then
随机生成新个体,替换个体x
end
end
计算种群Pt中每个个体的适应度值
fast-non-dominated-sort(Pt),将Pt中的非支配解以追加方式写入文档中
对种群Pt进行选择操作得到FP,|FP|=N/2
对FP进行交叉和变异操作产生新的种群FQ
Let Pt+1=FP∪FQ
Let t=t+1
end
对文档中的所有个体调用fast-non-dominated-sort,进行非支配排序与分层,仅保留分层结果的第一层即所有非支配解作为最优解集
算法2 计算支配关系(dominate)
输入:决策向量p,q
输出:p是否支配q
for对于每个目标函数fi(x) do
if fi(p) < fi(q) then
返回p不支配q
end
end
返回p支配q
算法3 快速非支配排序(fast-non-dominated-sort)
输入:种群Pt
输出:得到非支配排序与分层
for种群Pt中的每一个个体p do
Set Sp=Ø表示个体p所支配的个体集合
Set np=0表示支配个体p的所有个体的数目
for种群Pt中的每一个个体q do
if个体p dominate个体q then
Let Sp=Sp ∪ q
end
else if个体q dominate个体p then
Let np=np +1
end
end
if np==0 then
Let prank=1
Let F1=F1 ∪ p
end
end
Set i=1
while Fi≠ Ø do
Set Q=Ø
for Fi中的每一个个体p do
for Sp中的每一个个体q then
Let nq=nq -1
if nq==0 then
Let qrank=i+1
Let Q=Q ∪ q
end
end
end
Let i=i+1
Let Fi=Q
end
3 实验 3.1 实验数据为了避免实验数据的主观性因素,开发了模拟产生雇主需求数据的程序,该程序能够生成指定组数的模拟需求数据,每组随机生成一定数量的雇主和需求,并为每个需求随机分配权值和代价.为了保证实验结果具有统计学上的稳定性,本文随机产生了50组模拟需求数据对算法进行测试与评估,每组数据随机生成5~10个雇主,每个雇主随机产生5~50个需求,每个雇主的各需求权重之和为100,每个需求的代价取值范围为1~40人/天,控制输入系统开发总代价少于随机需求总代价以模拟产生雇主冲突.单个雇主模拟数据如表 1所示.
| 表 1 单个雇主模拟数据样例 Table 1 Simulating requirements data for individual stakeholder |
为了能够说明基于文档NSGA-Ⅱ算法优选的需求能够平衡雇主冲突,使得雇主总体满意度较高,且没有特别不满意的现象,通过平均满意度、最小满意度、满意度方差3个指标来衡量本文提出的优选算法的有效性.
3.2.1.1 平均满意度统计平均数是用于反映现象总体的一般水平,或分布的集中趋势.平均满意度能够反映出优选结果的一般水平,平均满意度越大,优选效果越优异.平均满意度的计算方法为
| $ A = \frac{1}{M}\sum\limits_{i = 1}^M {{f_i}} . $ |
式中fi表示对于当前选择的需求集第i个雇主的满意度值.
3.2.1.2 最小满意度最小满意度反映了系统中雇主满意度最差情况,最小值越小,存在特别不满意的雇主情况可能性越大.需求优选方法需要考虑全体雇主的满意度情况,若一个需求优选结果的最小满意度很小,说明该结果使得某一个或某一些雇主很不满意,这种优选结果不能被接受成为最终的需求.最小满意度计算方法为
| $ B = \min \left( {{f_1}, {f_2}, \cdots, {f_M}} \right). $ |
式中fi表示对于当前选择的需求集第i个雇主的满意度值.
3.2.1.3 满意度方差方差是各个数据与其算术平均数的离差平方和的平均数,它能准确地反映出数据的离散程度.为了能够反映经过模型优选系统需求后系统中雇主满意度处在较为集中的水平,本文将使用数据分析结果中满意度方差衡量系统的优选效果.满意度方差计算方法为
| $ C = \frac{1}{M}\sum\limits_{i = 1}^M {{{\left( {{f_i} - A} \right)}^2}} . $ |
式中:fi表示对于当前选择的需求集第i个雇主的满意度值,A表示所有M个雇主的平均满意度.
3.2.2 基线采用了基于需求实现难易程度的优选方法(简称开销优选)、基于需求重要程度的优选方法(简称权重优选)、基于NSGA-Ⅱ算法的优选方法作为基线方法,与本文提出的基于存档NSGA-Ⅱ算法进行了对比试验评价.
3.2.2.1 基于需求难易程度的优选方法基于需求难易程度的优选方法是指先不考虑系统需求的雇主区别,将所有雇主提出的需求统一按照需求实现开销顺序排序,选取从小到大累加开销和不大于开发预算的需求集合,然后求解各个雇主的满意度,简称为开销优选.
3.2.2.2 基于需求重要程度的优选方法基于需求重要程度的优选方法是指先不考虑系统需求的雇主区别,将所有雇主提出的需求统一按照雇主标注的需求权重顺序排序,按照权重从大到小顺序选取需求集合直到需求累加时间和大于开发周期,然后根据选出的需求集合求解各个雇主的满意度,简称为权重优选.
3.2.2.3 基于NSGA-Ⅱ算法的优选方法基于NSGA-Ⅱ算法的优选方法是采用传统NSGA-Ⅱ算法来解决多雇主多需求问题[14],参照基于存档NSGA-Ⅱ算法实现了基于NSGA-Ⅱ算法的需求优选方法.与该算法的对比试验可以说明本文算法对传统NSGA-Ⅱ算法改进的有效性.
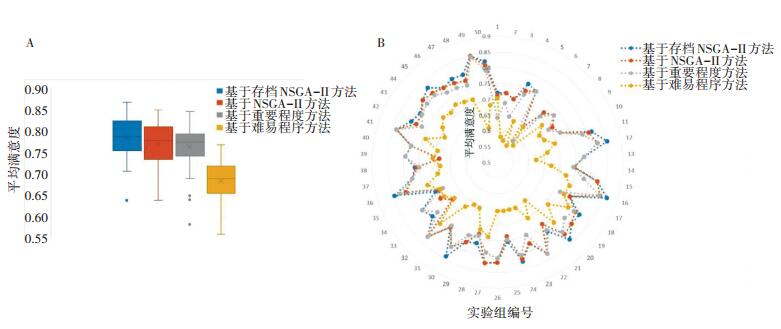
3.3 实验结果及分析 3.3.1 平均满意度实验结果平均满意度实验结果如图 5所示,实验结果表明,基于存档NSGA-Ⅱ算法的需求优选方法在50组随机需求数据中提出的需求优选方案表现优异,在绝大多数数据中,所选需求方案的平均满意度均为最佳,仅在少数测试集上略差于基线优选方法.因为基于难易程度优选方法与基于重要程度优选方法都仅考虑了需求实现的开支或雇主对需求的权重,而本文提出的方法通过对各个雇主的满意度进行多目标优化,同时考虑了需求实现的开支与权重,从而能够得到使得雇主更加满意的结果.
|
图 5 平均满意度实验结果 Figure 5 The result for average satisfaction |
基于传统NSGA-Ⅱ算法的需求优选方法在28组需求数据上与本文提出方法的结果相同,在22组需求数据上差于本文提出的方法.这是由于传统NSGA-Ⅱ算法没有在每次迭代过程中保留精英解,在迭代过程中,精英解可能丢失,从而导致最终的优化结果并非最优.本文提出的基于存档NSGA-Ⅱ算法则通过每次迭代将精英解保留至文档避免了精英解丢失的问题.
3.3.2 最小满意度实验结果最小满意度实验结果如图 6所示,实验结果表明,在多数随机产生的需求数据上,基于存档NSGA-Ⅱ算法的需求优选方法的最小满意度均高于基线优选方法.但在部分需求数据上,本文提出的需求优选方法劣于基线方法.其中基于NSGA-Ⅱ算法的需求优选方法与本文提出方法表现相近,但在22组数据上差于本文提出的方法.这主要是因为本文提出的基于存档NSGA-Ⅱ算法能够保留每次迭代过程的精英解,克服了传统NSGA-Ⅱ算法法精英解丢失的缺点.

|
图 6 最小满意度结果 Figure 6 The result for minimum satisfaction |
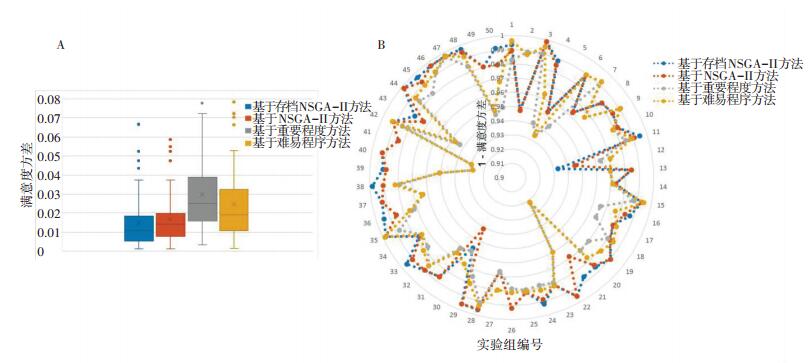
满意度方差实验结果如图 7所示,实验结果表明,在44个组需求数据集上,基于存档NSGA-Ⅱ算法的需求优选方法的结果满意度方差小与基于重要程度和基于难易程度两种优选方法,在其余6组需求数据集上满意度方差略大于这两种基线方法.在20组需求数据集上,本文提出的优选方法优于基于传统NSGA-Ⅱ算法的优选方法,在其余组需求数据上不差于NSGA-Ⅱ方法.这主要是因为本文提出的基于存档NSGA-Ⅱ算法的需求优选方法以每个雇主的满意度作为优化目标,优化的结果使每个雇主的满意度都尽可能达到最优,从而减少了雇主的满意度方差;基于存档NSGA-Ⅱ算法作为NSGA-Ⅱ算法的改进,在部分需求数据上,新方法由于避免了精英解丢失的情况,所以满意度方差小于传统方法.从实验结果可以得出结论,使用基于存档NSGA-Ⅱ算法的需求优选方法选择出的需求结果使得雇主满意度更加集中.
|
图 7 满意度方差结果 Figure 7 The result for variance in satisfaction |
综合上述实验结果,基于存档NSGA-Ⅱ算法的需求优选方法在平均满意度、最小满意度、满意度方差这3种评价指标上均优于开销优选方法和权重优选方法,这说明提出的基于存档NSGA-Ⅱ算法的需求优选方法能够在有效提高雇主整体满意度的同时,使雇主满意度更加集中.
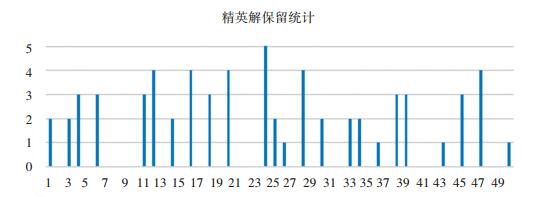
3.3.4 与NSGA-Ⅱ算法的比较结果从实验结果看,基于存档的NSGA-Ⅱ方法在全部的测试数据集上的表现均不差于NSGA-Ⅱ算法,在部分测试数据集上的表现优于NSGA-Ⅱ算法.因为基于存档的NSGAⅡ算法与NSGA-Ⅱ算法的主要不同在于保留每一次迭代的非支配解,优于NSGA-Ⅱ的那部分测试数据组即可说明提出的方法能够保留NSGA-Ⅱ在迭代过程中丢失的精英解.图 8给出了在50组测试集上,被NSGA-Ⅱ算法流失却被基于存档NSGA-Ⅱ算法获得的精英解个数.从图 8可以看出,基于存档的NSGA-Ⅱ算法确实能够保留NSGA-Ⅱ在迭代过程中丢失的精英解.
|
图 8 精英解保留结果 Figure 8 The statistics for the remaining elitist solution lost in NSGA-Ⅱ |
通过对软件工程中存在的多雇主需求优选问题进行了建模分析,提出了基于存档NSGA-Ⅱ算法的需求优选方法,实验结果表明,本文提出的方法能在满足雇主资源及需求实现成本的限制下,得到尽量使所有雇主满意的需求选择方案,为软件工程需求分析提供了客观、科学、合理的优选方案.
本文所阐述的方法是建立在雇主的需求之间不存在依赖性和相似性的前提下,这与实际情况相比还很理想化,如何提出一种更普遍并且有效的需求优选方法还有待于更深层次的研究.
| [1] |
陈建明. 软件需求工程及其发展[J].
装甲兵工程学院学报,2003, 17 (3) : 66-69.
CHEN Jianming. Review of software requirement engineering[J]. Journal of Armored Force Engineering Institute,2003, 17 (3) : 66-69. |
| [2] |
王达. 需求工程的探讨[J].
软件,2011, 32 (5) : 67-70.
WANG Da. Discussion of requirements engineering[J]. Software,2011, 32 (5) : 67-70. |
| [3] | DEB K, PRATAP A, AGARWAL S, et al. A fast and elitist multiobjective genetic algorithm: NSGA-Ⅱ[J]. IEEE Transactions on Evolutionary Computation,2002, 6 (2) : 182-197. DOI: 10.1109/4235.996017 |
| [4] |
赵君莉, 杨善学, 王宇平. 改进的非支配排序遗传算法INSGA-Ⅱ[J].
西安科技大学学报,2006, 26 (4) : 529-531.
ZHAO Junli, YANG Shanxue, WANG Yuping. An improved non-dominated sorting genetic algorithm INSGA-Ⅱ[J]. Journal of Xi'an University of Science and Technology,2006, 26 (4) : 529-531. |
| [5] | ZHANG Y. Multi-objective search-based requirements selection and optimization, department of computer science[D] London: King's College, 2010. |
| [6] | HARMAN M, MANSOURI S A, ZHANG Y. Search-based software engineering: trends, techniques and applications[J]. ACM Computing Surveys,2012, 45 (1) : 11. |
| [7] | HAMAN M, MANSOURI S A, ZHANG Yuanyuan. Search based software engineering: trends, techniques and applications[J]. ACM Computing Surveys,2012, 45 (1) : 17-20. |
| [8] | SRINIVAS N, DEB K. Muiltiobjective optimization using nondominated sorting in genetic algorithms[J]. Evolutionary computation,1994, 2 (3) : 221-248. DOI: 10.1162/evco.1994.2.3.221 |
| [9] | SRINIVAS N, DEB K. Multi-objective function optimization using nondominated sorting genetic algorithms[J]. Evolutionary Computation,1995, 2 (3) : 221-248. |
| [10] | ZHANG Y, HARMAN M, FINKELSTEIN A, et al. Comparing the performance of metaheuristics for the analysis of multi-stakeholder tradeoffs in requirements optimisation[J]. Information and software technology,2011, 53 (7) : 761-773. DOI: 10.1016/j.infsof.2011.02.001 |
| [11] | DURILLO J, ZHANG Y, ALBA E, et al. A study of the multi-objective next release problem[C]//1st International Symposium on Search Based Software Engineering. Windsor: IEEE, 2009: 49-58. |
| [12] | SALIU M, RUHE G. Bi-objective release planning for evolving software systems[C]//Proceedings of the 6thJoint Meeting of the European Software Engineering Conference And the ACM SIGSOFT Symposium on the Foundations Of Software Engineering. Dubrovnik: ACM, 2007: 105-114. |
| [13] | ZHANG Y, HARMAN M, MANSOURI S. The multi-objective next release problem[C]//Proceedings of the 9th Annual Conference on Genetic and Evolutionary Computation. ACM, 2007: 1129-1137. |
| [14] | CHARAN KUMARI A, SRINIVAS K, GUPTA MP. Software requirements selection using quantum-inspired elitist multi-objective evolutionary algorithm[C]/Proceedings of the IEEE-International Conference on Advances in Engineering, Science and Management.IEEE, 2012):782-787. |
| [15] | CAI X, LI Y, FAN Z, et al. An external archive guided multiobjective evolutionary algorithm based on decomposition for combinatorial optimization[J]. IEEE Transactions on Evolutionary Computation,2015, 19 (4) : 508-532. DOI: 10.1109/TEVC.2014.2350995 |
| [16] | PITANGUEIRA A M, TONELLA P, SUSI A, et al. Risk-aware multi-stakeholder next release planning using multi-objective optimization[C]//International Working Conference on Requirements Engineering: Foundation for Software Quality. Springer, 2016: 3-18. |
| [17] | KUMARI A C, SRINIVAS K. Comparing the performance of quantum-inspired evolutionary algorithms for the solution of software requirements selection problem[J]. Information and Software Technology,2016, 76 : 31-64. DOI: 10.1016/j.infsof.2016.04.010 |
| [18] | PITANGUEIRA A M, MACIEL R S P, BARROS M. Software requirements selection and prioritization using SBSE approaches: A systematic review and mapping of the literature[J]. Journal of Systems and Software,2014, 103 : 267-280. |
| [19] | DURILLO J J, ZHANG Y, ALBA E, et al. A study of the bi-objective next release problem[J]. Empirical Software Engineering,2011, 16 (1) : 29-60. DOI: 10.1007/s10664-010-9147-3 |
 2016, Vol. 48
2016, Vol. 48


