高分辨率图像所呈现的图像细节更为丰富,表达信息的能力更强,在医学、军事、遥感、视频监控等领域都有广泛应用.然而直接捕获的图像由于成像设备及采集环境的限制,往往存在模糊、变形、含噪声等.为了提高图像的分辨率,最直观的方法即为改善成像设备,然而高昂的费用限制了其应用范围,因而通过软件的方法来提高图像分辨率成为当前重要的研究领域之一.
基于学习的单帧图像超分辨率(SR)是图像重建的一个重要分支,即输入一幅低分辨率图像,预测对应的高分辨率图像,主要方法有:局部线性嵌入方法(LLE)[1]、核岭回归方法(KRR)[2]、稀疏表示方法[3-5],及一些方法寻求准确的模糊核[6-7]来进行超分辨率.其中Yang提出的稀疏编码方法(SCSR)[3]将压缩感知理论开创性地应用到了超分辨率中,利用稀疏表示这个强先验知识,取得了较好的效果.文献[4]提出了耦合字典训练方法,提高了算法的计算效率,文献[5]进一步改进了该算法,提高了算法的稳定性.但是这类方法大多数采用一阶梯度及二阶梯度(水平、垂直方向)来提取图像的高频信息,并不能提取任意方向的信息,因此该特征描述的信息并不全面.非下采样轮廓波变换(NSCT)具有多尺度性、多方向性、平移不变性,能够提取多方向多尺度的信息. Amisha[8]在超分辨率中引入了该变换,复原了更多的图像高频信息,但是相对而言,NSCT不能很好地提取图像细节纹理信息. Gabor变换[9-11]由于其有效性,被广泛地用于纹理分析,因此可以结合NSCT与Gabor的优势,对图像进行综合特征提取.
本文尝试利用NSCT与Gabor变换的互补性,针对不同特征的低分辨率图像块采用不同的方法进行提取,然后分别在稀疏表示的框架下对图像块进行稀疏重构,最后合并成一幅高分辨率图像,意在提高图像的超分辨率效果.另外,由于图像或多或少都存在模糊,本文尝试加入去模糊正则项,使算法能够处理模糊输入的情况.
1 基于稀疏表示的超分辨率算法近十年来,稀疏表示作为一个强有力的工具被广泛地用于图像去噪、压缩、超分辨率中[12].其主要思想是对于一个给定的信号y∈Rn,可以由过完备字典D∈Rn×m(n < m)基元的线性组合来表示,即y=Dα,其中α∈Rm为稀疏表示的系数(仅含有少量的非零元素).该系数α可以通过求解下面的优化问题得到:
| $ \mathop {\min }\limits_\alpha {\left\| \alpha \right\|_0},\;\;\;\;{\rm{s}}{\rm{.t}}{\rm{.}}\left\| {y - D\alpha } \right\|_2^2 \le \varepsilon . $ | (1) |
该模型表示在满足误差ε下,l0范数准则下最小的α.然而,式(1)求解是NP困难问题,为解决该问题,文献[13]提出可以用l1范数来逼近l0,即
| $ \mathop {\min }\limits_\alpha {\left\| \alpha \right\|_1},\;\;\;\;{\rm{s}}{\rm{.t}}{\rm{.}}\left\| {y - D\alpha } \right\|_2^2 \le \varepsilon . $ | (2) |
式(2)为凸优化问题,利用拉格朗日乘数因子λ,该式就转变成了数学上的套索问题[14],即
| $ \mathop {\min }\limits_\alpha \lambda {\left\| \alpha \right\|_1} + \left\| {y - D\alpha } \right\|_2^2. $ | (3) |
通过求解式(3),就可以得到信号y在字典D下的稀疏表示系数α.
SCSR[3]方法将稀疏表示的理论用于图像超分辨率中,其基本思想是首先从训练集中构造一个描述高低分辨率图像块对应关系的过完备字典,然后寻求每一个待重建的图像块在该字典下的稀疏表示系数,最后利用该系数构造出高分辨率图像.整体过程分为字典训练部分与稀疏重构部分,其中字典训练部分采用联合训练的方式,即
| $ \mathop {\min }\limits_{\left\{ {{D_{\rm{h}}}, {D_{\rm{l}}}, Z} \right\}} \left\| {{X_c} - {D_c}Z} \right\|_2^2 + \hat \lambda {\left\| Z \right\|_1}, $ |
式中
| $ {X_c} = \left[\begin{array}{l} \frac{1}{{\sqrt N }}{X^{\rm{h}}}\\ \frac{1}{{\sqrt M }}{Y^{\rm{l}}} \end{array} \right], {D_c} = \left[\begin{array}{l} \frac{1}{{\sqrt N }}{D_{\rm{h}}}\\ \frac{1}{{\sqrt M }}{D_{\rm{l}}} \end{array} \right]. $ |
{Xh, Yl}表示训练集中高低分辨率图像块(特征),{Dh, Dl}表示高低分辨率字典,Z表示系数,{N, M}表示高低分辨率图像块以向量表示的维数.通过联合训练方式,实现了高分辨率图像块的稀疏表示系数与对应的低分辨率图像块的系数相同的先验知识.稀疏重构部分主要分为基于稀疏表示的局部模型构建和全局重建约束两部分,分别是
| $ {\alpha ^*} = \arg \min \left\| {D\alpha - y} \right\|_2^2 + \lambda {\left\| \alpha \right\|_1},{X_0} = {D_{\rm{h}}}{\alpha ^*}. $ | (4) |
| $ {X_1} = \mathop {\arg \min }\limits_X \left\| {SBX - y} \right\|_2^2 + c\left\| {X - {X_0}} \right\|_2^2. $ | (5) |
式中:α*表示稀疏表示系数,y表示低分辨率图像,S表示下采样操作,B表示模糊操作,X1表示稀疏重构后的高分辨率图像.利用式(4)可以求得图像块y的稀疏表示系数α*,由于图像结构的相似性,高低分辨率图像块在各自字典下具有相同的稀疏表示系数,因此可以利用该系数α*与高分辨率图像字典Dh构造出初始的高分辨率图像X0.由于低分辨率图像本身存在一些噪声,在式(4)过程中也可能会造成一定的人工伪迹,为去除这些影响,利用式(5)加强重建约束,这样就得到了最终的高分辨率图像X1.
2 本文算法在图像超分辨率中,主要恢复图像的高频信息,因此无论是在字典训练过程还是稀疏重构部分,首要步骤就是提取低分辨率图像的高频信息,以便对丢失的信息做更为准确的预测,故特征提取方法成为超分辨率效果的关键因素之一.
大多数方法采用一阶梯度及二阶梯度来提取图像的高频信息,但是,由于梯度只能沿水平、垂直方向,不能全面描述图像的高频信息.为克服该缺点,采用NSCT与Gabor相结合的方式来提取特征.图像在降质过程中丢失的高频信息一般为纹理信息和轮廓信息,因此,重点恢复这两类信息.对低分辨率图像块进行了分类,依据小块的方差分成平坦块(小方差)和非平坦块(大方差).首先来观察这两类图像块的特点,一般来说,对于平坦块,其纹理特征较为丰富,而对于非平坦块,其轮廓特征较为丰富.在图 1中,将lena图像块分成了两类,其块大小选取的是25*25,归一化后图像块方差选取的是0.22,左图为平坦块,右图为非平坦块.从图 1可以看到,左图细节纹理信息较多,而右图轮廓边缘信息较丰富.

|
图 1 方差分类图 Figure 1 The classification diagram for variance |
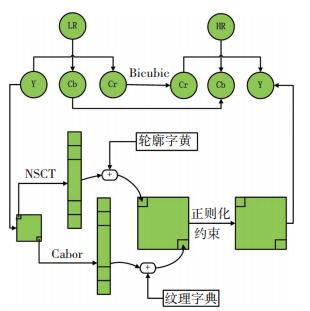
针对图像块的特点,对于平坦块,重点复原纹理信息,利用Gabor滤波器提取小块的纹理特征,进而求出在纹理字典库下的稀疏表示系数,再利用该系数进行纹理信息重构;而对于非平坦块,重点恢复其轮廓信息,利用NSCT提取小块的轮廓特征,类似地,求出其在轮廓字典库下的稀疏表示系数,利用该系数进行轮廓信息的重构,最后,将重建的图像块组合成一副完整的图像.另外,图像在降质过程中或多或少会造成图像模糊,因此在稀疏重构过程中,对图像进行了整体优化,加入了去模糊的正则项,以消除模糊的影响.算法总体流程图如图 2所示.
|
图 2 算法流程图 Figure 2 The flow diagram of the proposed algorithm |
本算法的改进点主要有两方面:一是将低分辨率图像块进行了分类,针对不同的图像块提取不同的特征;二是在超分辨率过程中加入了去模糊正则项,消除了模糊输入的影响.
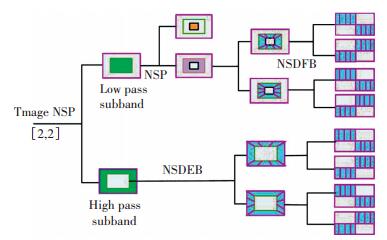
2.1 提取图像块的特征由于人类视觉系统对图像的轮廓信息极其敏感,因此有效复原图像的轮廓信息相当重要. NSCT不仅具有良好的多方向性和多尺度性,还具有平移不变性,能够有效地提取图像的轮廓特征. NSCT由非下采样金字塔(NSP)分解和非下采样方向滤波器组(NSDFB)分解组成.以两层NSP分解和两层NSDFB分解为例,阐述图像分解过程.图像首先经NSP分解得到一个高频子带和一个低频子带,然后采用NSDFB对高频子带进行方向分解,若方向分解系数为m,则得到2m个高频子带.而下一次NSP分解再对上一层NSP分解得到的低频图像进行分解,因此经过两层NSP分解和两层NSDFB分解,可以得到1个低频子带和8个高频子带.相比较梯度特征,NSCT可以得到更多尺度与方向的信息,对图像的描述能力更强.图 3为具有两层NSP分解与两层NSDFB分解的NSCT的结构图.
|
图 3 NSCT结构图(两层NSP分解与两层NSDFB分解) Figure 3 NSCT with two-level NSP decomposition and two-level NSDFB decomposition |
另外,除了图像的轮廓信息,纹理信息也极为重要.在图像分析领域,Gabor变换已经成功地用于提取图像的纹理特征.与NSCT变换相比,Gabor变换能够更好地提取图像的细节信息,其由不同方向不同频率的滤波器组组成,同样具有多方向性、多尺度性以及平移不变性.二维的Gabor函数[15]如下式所示:
| $ G\left( {x, y} \right) = \frac{1}{{\sqrt {2\pi } {\sigma ^2}}}{{\rm{e}}^{ - \left( {\frac{{{x^{'2}} + {y^{'2}}}}{{2{\sigma ^2}}}} \right)}}{{\rm{e}}^{{\rm{j2\pi }}\left( {\mu x' + vy'} \right)}}. $ |
式中:x′=xcos θ+ysin θ, y′=-xsin θ+ycos θ,σ为高斯沿x轴和y轴的标准偏差,(μ, ν)为空间频率.
综合NSCT与Gabor变换各自的优势,用NSCT来提取图像块的轮廓信息,用Gabor变换来提取纹理信息,这样,图像的轮廓及纹理信息被有效地提取出来.图像块通过NSCT生成的各个子带级联成一个向量作为图像块的轮廓特征,同样,图像块经过Gabor变换得到的各个子带也被级联成一个向量作为图像块的纹理特征.
2.2 正则化约束图像在降质过程中或多或少会变得模糊,因此在超分辨率过程中,去除模糊的能力也成为影响其效果的关键因素.对于图像去噪、去模糊、超分辨率这类不适定的反问题,为了逼近原图像信息的解,必须加入额外的先验知识来使解稳定,这类方法统称为正则化方法,故需要寻求合适的去模糊正则项.
很多含参的图像先验方法被用于求解这类问题,最简单的方法是使用高斯平滑惩罚项,但是效果并不好.后来开始使用lp(0.7≤p≤1)范数[16]来反映图像的统计特性,还有很多复杂的方法尝试学习一些滤波器及代价函数[17-18].这些方法已经成功地用于图像去噪,但对于图像去模糊是不适用的,因为模糊操作会削弱图像的高频信息,这将会导致模糊图像比清晰图像有一个更低的代价.例如单纯地最小化l1范数,可以去除一定的噪声,然而会得到一幅比较模糊的图像[19].而l1/l2(L1范数/L2范数)有效地解决了这个问题,该正则项会随着图像模糊程度的增加而增大,故可以通过最小化该参数以达到去模糊的效果[20]. l1/l2相比较l1而言,能够更准确地描述清晰图像的特点,无论模糊操作还是锐化操作,都将使其增大,即真实图像的l1/l2最小.因此采用l1/l2作为去模糊的正则项.
在求解过程中,由于图像的低频子带几乎不受模糊的影响,因此首先提取重建完初始的高分辨率图像的梯度特征(水平、垂直方向),然后通过求解式(6)(最小化l1/l2)来得到模糊核,进而利用文献[21]的模糊算法得到高分辨率图像.正则项约束为
| $ \underset{X,B}{\mathop{\min }}\,\lambda \left\| BX-X_{1}^{'} \right\|_{2}^{2}+\frac{{{\left\| X \right\|}_{1}}}{{{\left\| X \right\|}_{2}}}+\varphi {{\left\| B \right\|}_{1}}. $ | (6) |
式中X′1表示图像的梯度特征,B为模糊核.式(6)的解可以通过交替求模糊核B和清晰图像X得到.求模糊核B时采用IRLS算法[22],求清晰图像时采用ISTA算法[23],其能够快速地求解一般的线性逆问题.
2.3 超分辨率详细算法首先训练纹理字典及轮廓字典作为输入(训练方法见2.4节),超分辨率过程主要分为两部分:稀疏表示模型和正则化约束.稀疏表示模型主要利用稀疏表示先验构造出初始的高分辨率图像,而正则化约束则是对初始的高分辨率图像进行优化,去除人工伪迹及模糊、噪声的影响.
1)稀疏表示模型.将低分辨率图像划分成小块,依据小块方差分为平坦块与非平坦块.对于平坦块,用Gabor滤波器提取其纹理特征,利用式(4)在纹理字典库下求得对应的高分辨率图像块;对于非平坦块,用NSCT提取其轮廓特征,同样的方法,求得其在轮廓字典下对应的高分辨率图像块,最后将图像块组合成完整的初始的图像.
2)正则化约束.正则化约束条件有两个:一是式(5)保证重建约束,由于初始图像含有噪声及在1)过程中可能产生不必要的人工伪迹,该正则化约束主要是去除这些影响;二是式(6)去除模糊的影响,使算法能够处理模糊输入的情况.具体的算法如下.
算法1 整体的超分辨率算法框架.
输入:一幅低分辨率图像Y,纹理字典{Dhc, Dlc},轮廓字典{Dhg, Dlg}.
从Y的左上角开始,对于每一个5*5的图像块yj(块与块之间重叠4个像素点)执行以下步骤:
1)计算yj的方差.若方差大于θ,则用NSCT提取图像块的轮廓特征,在以下的步骤中采用轮廓字典;相反,若方差小于θ,则用Gabor滤波器提取图像块的纹理特征,在下列步骤中采用纹理字典.
2)利用式(4)求得图像块在对应字典下的稀疏表示系数,再利用相同的系数及对应的高分辨率图像字典求得初始的高分辨率图像X0.
| $ {\alpha ^*} = \arg \min \left\| {D\alpha - y} \right\|_2^2 + \lambda {\left\| \alpha \right\|_1}, {X_0} = {D_{\rm{h}}}{\alpha ^*}. $ |
利用式(5)求得满足重建约束并最接近X0的图像X1.
| $ {X_1} = \mathop {\arg \min }\limits_X \left\| {SBX - Y} \right\|_2^2 + c\left\| {X - {X_0}} \right\|_2^2. $ |
消除模糊输入的影响并重建出最终的高分辨率图像X*.
1)利用式(6)求得模糊核B*.
| $ {B^*} = \mathop {\arg \min }\limits_B \lambda \left\| {BX - {X_1}} \right\|_2^2 + \frac{{{{\left\| X \right\|}_1}}}{{{{\left\| X \right\|}_2}}} + \varphi {\left\| B \right\|_1}. $ |
2)在模糊核B*下,利用去模糊算法[20]恢复出图像X*.
输出:高分辨率图像X*.
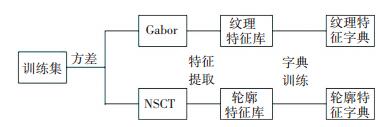
2.4 字典训练在图像超分辨率过程中,将低分辨率图像块分成了平坦块与非平坦块,分别复原其纹理信息及轮廓信息,因此,需要训练两个字典:纹理字典及轮廓字典.对于纹理字典,首先随机挑选训练库中方差比较小的图像块,进而采用Gabor滤波器提取其纹理特征,生成纹理特征库,对纹理特征库进行联合训练,便得到了纹理特征字典.同样地,对于轮廓字典,选取方差比较大的图像块,用NSCT提取其轮廓特征进行字典的训练.字典训练方法与SCSR训练字典的方法相同,具体训练流程见图 4.
|
图 4 字典训练流程图 Figure 4 The flow chart of the dictionaries training |
为了说明算法的可行性和有效性,分别做了以下对比实验.采用和SCSR方法相同的训练集,测试图像从USC-SIPI,Flickr收集,另外还收集了一些经典图像作为测试图像.在字典训练过程中,采用归一化后的图像块方差0.27作为区分平坦块和非平坦块的阈值,进而进行纹理字典及轮廓字典的训练.为得到与高分辨率图像相对应的低分辨率图像,首先将测试图像降采样2倍,再用5×5的高斯模糊核或运动模糊核对其进行模糊处理.综合考虑算法的复杂度及准确性,采用2个尺度、4个方向的Gabor滤波器组对图像块进行纹理特征的提取,采用两层NSP及两层NSDFB分解的NSCT对图像块进行轮廓特征的提取.在超分辨率中,选择5×5的小块作为单位进行超分辨率.分别讨论特征、去模糊项、字典大小对超分辨率效果的影响以及不同超分辨率方法的对比,实验效果采用PSNR值进行评估,PSNR值越高代表重建效果越好.
3.1 特征对超分辨率效果的影响首先用方差为1的高斯模糊核对15幅图像进行模糊处理,然后分别采用Gabor、NSCT以及两种结合的方式(本方法)提取图像的特征,再分别进行超分辨率.另外,将SCSR方法作为参照.采用各种方法进行超分辨率的PSNR值在表 1中显示,从表 1可以看出,采用NSCT与Gabor相结合的方式进行超分辨率的PSNR值是最高的,因而从客观上说明结合这两种方法是有效的.对松鼠这幅图像采用不同特征提取方法进行超分辨率的效果如图 5所示,从图像中可以观察到采用NSCT及Gabor相结合方式的超分辨率图像更为清晰.

|
图 5 松鼠的超分辨率效果(不同特征提取方法) Figure 5 Results of the squirrel image with different features |
| 表 1 不同特征提取方法的对比 Table 1 PSNR values with different feature extraction methods |
用运动模糊核(分别沿45度角移动3,4,5,6个像素)将23幅图像进行模糊处理,再分别用SCSR方法与本方法进行超分辨率,其PSNR值如表 2所示.表中最后一行为(3,45)行与(6,45)行PSNR值的差值.从表 2可以看到,随着输入图像运动模糊程度的加深,SCSR方法重建出的图像PSNR值下降的非常快,即超分辨率效果迅速变差,而本文方法重建出的图像PSNR值下降的相对缓慢,这说明模糊正则项的加入是有效的. img1的重建效果如图 6所示,从图 6可以观察到,SCSR方法由(3,45)到(6,45)重建出的图像效果差别很大,而本文方法差别比较小,从感官上说明了模糊正则项的有效性.

|
图 6 img1的超分辨率效果(不同模糊输入) Figure 6 Results of the img1 with different blur degrees |
| 表 2 不同模糊程度的输入的对比 Table 2 PSNR values of different blur degrees |
首先训练大小为256、512、1024的三类字典,每一类字典都包括本文算法用到的纹理字典、轮廓字典以及SCSR方法的字典,然后分别用SCSR方法、本文方法进行重建,输入图像用方差为1的高斯模糊核进行模糊处理,其超分辨率图像对应的PSNR值如表 3所示,最后一行是23幅图像的平均值.从表 3可以看出,就平均值而言,字典越大, PSNR值越高, 即图像复原效果越好,这是符合人们的直觉认识.更重要的是,对于相同规模的字典,本文方法的PSNR值都比SCSR方法高,这也说明了本文算法的有效性.
| 表 3 字典大小对超分辨率效果的影响 Table 3 PSNR values with different sizes of dictionary |
将本文方法与Bicubic差值、SCSR[3]、KRR[2]方法进行了对比,表 4展示了使用不同方法对图像进行超分辨率的PSNR值,其中lena,peppers采用方差为1的高斯模糊核进行模糊处理,Gaussian(5, 1)行展示的是43幅图像PSNR的平均值.这组图像采用方差为1的5×5高斯模糊核进行处理,Motion(5,45)也是43幅图像PSNR的平均值,该组图像采用5×5的运动模糊核(沿45度运动了5个像素值)进行模糊处理,其余同理.从表 4可以观察到,本文方法的PSNR值相比较SCSR、KRR提高了大概2 dB.对lena及peppers进行重建的图像如图 7、图 8所示,从图中可以观察到本方法重建出的图像更为清晰.

|
图 7 lena的超分辨率效果,从左往右依次是:原始输入图片,SCSR,KRR,Ours,Truth Figure 7 Results of the lena image. Left to right: Input, SCSR, KRR, Ours, Truth |

|
图 8 peppers的超分辨率效果,从左往右依次是:原始输入图片,SCSR,KRR,Ours,Truth Figure 8 Results of the peppers image. Left to right: Input, SCSR, KRR, Ours and Truth |
| 表 4 不同方法间的对比 Table 4 PSNR values of SR images with different methods |
结合多特征融合和稀疏表示的超分辨率方法,利用NSCT与Gabor的互补性,针对不同的低分辨率图像块,采用不同的方法来提取特征,进而进行重建.此外,算法针对SCSR方法处理模糊输入情况较差的缺点,加入了去模糊正则项,使得算法能够较好地处理模糊输入的情况,最终使得重建后的图像较好地复原了丢失的高频信息.通过各方面的实验验证了该算法的有效性.
| [1] | CHANG H, YEUMG D Y, XIONG Y. Super-resolution through neighbor embedding[C]// Proceedings of the 2004 IEEE Computer Society Conference onComputer Vision and Pattern Recognition.Washington, DC:IEEE, 20041:275-282. |
| [2] | KIM K I, KWON Y. Single-image super-resolution using sparse regression and natural image prior[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence,2010, 32 (6) : 1127-1133. DOI: 10.1109/TPAMI.2010.25 |
| [3] | YANG J, WEIGHT J, HUANG T S, et al. Image super-resolution via sparse representation[J]. IEEE Transactions onImage Processing,2010, 19 (11) : 2861-2873. DOI: 10.1109/TIP.2010.2050625 |
| [4] | YANG J, WANG Z, Lin Z, et al. Coupled dictionary training for image super-resolution[J]. IEEE Transactions on Image Processing,2012, 21 (8) : 3467-3478. DOI: 10.1109/TIP.2012.2192127 |
| [5] | PELEG T, ELAD M. A statistical prediction model based on sparse representations for single image super-resolution[J]. IEEE Transactions on Image Processing,2014, 23 (6) : 2569-2582. DOI: 10.1109/TIP.2014.2305844 |
| [6] | MICHAELI T, IRANI M. Nonparametric blind super-resolution [C]//Proceedings of the IEEE International Conference on Computer Vision. Sydney: IEEE, 2013: 945-952. https://www.computer.org/csdl/proceedings/iccv/2013/2840/00/index.html |
| [7] | EFRAT N, GLASNER D, APARTSIN A, et al. Accurate blur models vs. image priors in single image super-resolution [C]// Proceedings of the IEEE International Conference on Computer Vision. Sydney: IEEE, 2013: 2832-2839. http://dl.acm.org/citation.cfm?id=2587071 |
| [8] | SHAH A J, MAKWANA R, GUPTA S B. Single image super-resolution via non sub-sample contourlet transform based learning and a Gabor prior[J]. International Journal of Computer Applications,2013, 64 (18) : 32-38. DOI: 10.5120/10735-5580 |
| [9] | ACHARYA T, RAY A K. Image processing: principles and applications[J]. Journal of Electronic Imaging,2006, 15 (3) : 579-584. |
| [10] | WU J, WEI Z, CHANG Y. Color and texture feature for content based image retrieval[J]. International Journal of Digital Content Technology & Its Applications,2010, 4 (4) : 43-49. |
| [11] | DO M N, VETTERLI M. Wavelet-based texture retrieval using generalized Gaussian density and Kullback-Leibler distance[J]. IEEE Transactions on Image Processing,2002, 11 (2) : 146-158. DOI: 10.1109/83.982822 |
| [12] | ELAD M. Sparse and redundant representations: from theory to applications in signal and image processing[M]. New York: Springer, 2010 . |
| [13] | CHEN S S, DONOHO D L, SAUNDERS M A. Atomic decomposition by basis pursuit[J]. SIAM review,2001, 43 (1) : 129-159. DOI: 10.1137/S003614450037906X |
| [14] | TIBSHIRANI R. Regression shrinkage and selection via the lasso[J]. Journal of the Royal Statistical Society,1996, 58 (1) : 267-288. |
| [15] |
吴高洪, 章毓晋, 林行刚. 分割双纹理图像的最佳Gabor滤波器设计方法[J].
电子学报,2001, 29 (1) : 48-50.
WU Gaohong, ZHANG Yujin, LIN Xinggang. Optimal Gabor filter design for bi-textured image segmentation[J]. Chinese Journal of Electronics,2001, 29 (1) : 48-50. |
| [16] | GUPTA A, JOSHI N, ZITNICK C L, et al. Single image deblurring using motion density functions[C]//Computer Vision-ECCV 2010. Berlin: Springer, 2010: 171-184. http://link.springer.com/content/pdf/10.1007/978-3-642-15549-9_13.pdf |
| [17] | WEISS Y, FREEMAN W T. What makes a good model of natural images?[C]// IEEE Conference on Computer Vision and Pattern Recognition. Puerto Rico:IEEE, 2007: 1-8. |
| [18] | ROTH S, BLACK M J. Fields of experts: a framework for learning image priors[C]// IEEE Computer Society Conference on Computer Vision and Pattern Recognition. San Diego:IEEE, 2005, 2: 860-867. http://www.oalib.com/references/16890794 |
| [19] | LEVIN A, WEISS Y, DURAND F, et al. Understanding and evaluating blind deconvolution algorithms[C]// IEEE Conference on Computer Vision and Pattern Recognition. Miami:IEEE, 2009: 1964-1971. |
| [20] | KRISHNAN D, TAY T, FERGUS R. Blind deconvolution using a normalized sparsity measure[C]// IEEE Conference on Computer Vision and Pattern Recognition. Colorado Spribgs: IEEE, 2011: 233-240. |
| [21] | ZORAN D, WEISS Y. From learning models of natural image patches to whole image restoration[C]// IEEE International Conference on Computer Vision. Barcelona:IEEE, 2011: 479-486. |
| [22] | LEVIN A, FERGUS R, DURAND F, et al. Image and depth from a conventional camera with a coded aperture[J]. ACM Transactions on Graphics,2007, 26 (3) : 70. DOI: 10.1145/1276377 |
| [23] | BECK A, TEBOULLE M. A fast iterative shrinkage-thresholding algorithm for linear inverse problems[J]. SIAM Journal on Imaging Sciences,2009, 2 (1) : 183-202. DOI: 10.1137/080716542 |
 2016, Vol. 48
2016, Vol. 48


