室外自然场景捕获对于理解自然环境和执行可视化活动,如对象检测、识别和导航,是十分重要的.但是在恶劣天气环境下,光受大气颗粒的吸收或散射使场景可见度和对比度大大降低,颜色发生偏移和特征信息大量减少[1],进而降低识别和检测的效果,所以图像去雾技术逐渐受到了研究人员的关注.
基于物理模型研究图像去雾,最早是利用暗对象相减来处理多光谱数据[2]对大气散射校正或利用同一场景不同天气状况下的多幅图像进行除雾.后来,近似3D场景模型得到使用. Hautiere等[3]提出利用无雾的车辆视觉系统进行对比度恢复,Kopf等[4]利用现有的地理数字城市模型生成深度图来提高图像可见度.然而获得足够的图像或获取精确的3D地理模型是非常费时和困难的,所以单幅图像除雾方法的研究显得尤为重要.在单幅有雾图像处理方法中,大部分除雾算法都假设图像满足大气散射模型[5],利用一个附加的深度估计图或单独的投射图来增强图像的可见度.Tan[6]通过最大化局部对比度来预测场景反照率,但结果往往过饱和并出现“halo效应”.Fattal[7]假定传输和表面模型是统计不相关来提高图像对比度,但该方法需要知道有雾场景下大量的颜色和亮度信息.Tarel等[8]提出了一种使用中值滤波的快速算法,但所提取的深度图在边缘细节上不能很好保持.He等[9]在暗通道先验方面作出重大贡献,通过加入先验约束条件,使用软抠图方法对初始投射图进行细化并取得成功的处理结果.然而软抠图在计算上十分耗时,尽管后来使用导向滤波来进行加速[10],但计算复杂度还是比较高,另外在天空区域和边缘区域存在处理效果不佳等问题.
本文结合融合框架[11]对原有暗原色先验方法的不足提出了一些改进措施:为了减少原方法块操作所带来的“halo效应”,在投射图计算中加入图像块的加权插值技术,一定意义上消除了“halo效应”;针对原色先验在天空或明亮区域的损失,提出一种自适应暗原色先验模型,提高模型的鲁棒性和适用范围;针对暗原色先验处理后的图像颜色偏暗,在雾浓度偏高地方细节特征变少的问题,结合白平衡处理后图像和雾浓度感知预测模型处理后的图像进行融合,在增加雾浓度过高区域特征信息的同时,还可以使图像整体颜色更加自然.
1 基于物理模型的图像去雾算法 1.1 大气散射模型-雾天图像降质的物理原理在雾霾天气条件下,大气中悬浮的大量粒子对光线有较强的散射作用.一方面物体表面的反射光由于大气粒子的散射而发生衰减,光强的衰减直接导致物体成像的亮度减弱,而前向散射也会导致图像模糊分辨力下降;另一方面自然光因大气粒子的后向散射而进入成像传感器参与成像,这种后向散射作用造成图像饱和度、对比度降低及色调发生偏差[5].
理论上,根据暗原色先验模型,一幅含雾图像I可以被分解成两个分量,直接衰减项和大气光成分项,即
| $ \mathit{\boldsymbol{I}}\left( x \right) = \mathit{\boldsymbol{J}}\left( x \right)t\left( x \right) + \mathit{\boldsymbol{A}}\left[{1-t\left( x \right)} \right]. $ |
式中:I(x)是观察者接收的有雾图像在x处的亮度,J(x)是观察者应该接收到的图像,t(x)∈[0, 1]是大气反射光的投射图,A代表周围环境的大气光成分.第一项J(x)t(x)是直接衰减项,表示场景辐射率如何随着媒介进行衰减的.第二项A[1-t(x)]称为大气光成分,由于先前的散射光会造成场景颜色偏移.一般来说,通过假定大气是均匀的,并且光传播更长的距离时会加块衰减和散射.其中t(x)=e-βd(x)中β是介质的衰减系数,d(x)是场景和观察者之间的距离.
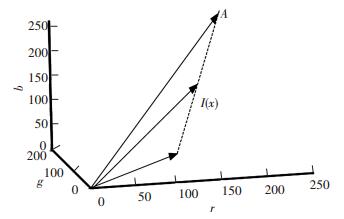
雾天图像的成像模型如图 1所示, 它揭示了从图像复原角度实现去雾的核心思想, 即从观测到的图像亮度中去除大气光参与成像的部分, 同时对衰减光的结果进行补偿, 即可实现场景的清晰复原.它意味着在RGB色彩空间中, 向量A, J(x),I(x)从几何学来看是共面的, 端点是共线的, 透过系数t是两条线段长度之比[9], 即
|
图 1 雾天图像成像模型 Figure 1 Haze imaging model |
| $ t\left( x \right) = \left\| {\frac{{\mathit{\boldsymbol{A}} - \mathit{\boldsymbol{I}}\left( x \right)}}{{\mathit{\boldsymbol{A}} - \mathit{\boldsymbol{J}}\left( x \right)}}} \right\|. $ |
利用大气散射模型将有雾图像恢复到无雾图像的方法总体上可以分为三类:第一类是基于深度信息的方法;第二类是基于大气光偏振特性的去雾算法;第三类是基于先验知识的方法.
1.2 暗通道先验暗原色先验是一种对无雾图像的统计学规律.先前的去雾方法重心都是放在提高图像对比度上,而He等人着眼于无雾图像的统计特征,通过对收集到的大量的无雾图像做实验,发现了这个客观存在的统计规律,即在绝大多数户外无雾图像的任意局部小块中,总存在一些(至少一个)像素,它们的某一个或几个颜色通道的强度值很低且接近于零,称之为暗原色[9].
在暗原色的求取过程中, 首先将雾图像在RGB空间进行分解, 在局部块中取最小值操作, 求得R, G, B三通道中最小分量, 然后采用软抠图或导向滤波算法[10]对最小分量值进行局部区域最小滤波.求取暗通道的数学表达式为
| $ {\mathit{\boldsymbol{J}}^{{\rm{dark}}}}\left( x \right) = \mathop {\min }\limits_{y \in \mathit{\Omega }\left( x \right)} \left( {\mathop {\min }\limits_{c \in \left\{ {r, g, b} \right\}} {\mathit{\boldsymbol{J}}^c}\left( y \right)} \right). $ | (1) |
式中:Jc(y)表示彩色图像的每个通道, Ω(x)表示以像素x为中心的一个窗口.式(1)的表达也很简单, 首先求出每个像素RGB分量中的最小值, 存入一幅和原始图像大小相同的灰度图中, 然后再对这幅灰度图进行最小值滤波, 滤波的半径由窗口大小决定, 一般有WindowSize=2 * Radius + 1.暗通道先验的理论指出:Jdark(x)→0.
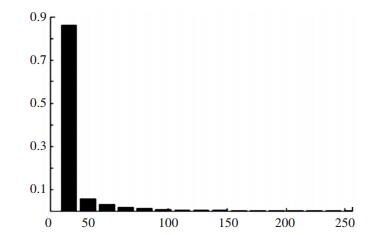
暗原色先验理论是基于统计学上的规律,目前还没有被数学证明.为了验证其有效性和正确性,He等做了大量的统计实验,图 2给出了超5 000幅图像的暗原色强度统计直方图,从中可以看出约有75%的像素点,其强度值为0,约有86%的像素点,其强度值低于16,绝大多数的像素点的强度值都很低.以上统计结果在一定程度上证明了暗原色先验的合理性.因此He得出结论:绝大多数户外无雾图像中的暗原色都具有较低的平均强度值,这就意味着在无雾图像中绝大多数都符合暗原色先验规律.
|
图 2 超过5 000幅图像暗通道先验强度统计直方图 Figure 2 Histogram of the intensity of the pixels in all the 5 000 dark channels |
雾浓度感知预测模型[12]首先从测试集中提取雾统计特征,然后通过高斯模型对雾统计特征进行拟合,进而计算自然无雾图像和含雾图像的偏差.雾统计特征是通过自然场景统计模型和雾统计特征派生出来的.雾感知密度可以表示为有雾图像等级与无雾图像等级的比率.该比率方法包含有雾图像与无雾图像的特征,因此比单纯利用有雾图像预测雾浓度更准确[13].
高斯模型表达式为
| $ {\rm{MVG}}\left( \mathit{\boldsymbol{f}} \right) = \frac{1}{{{{\left( {2{\rm{ \mathsf{π} }}} \right)}^{d/2}}{{\left| \sum \right|}^{1/2}}}}\exp \left[{-\frac{1}{2}{{\left( {\mathit{\boldsymbol{f}}-\mathit{\boldsymbol{v}}} \right)}^t}{\sum ^{-1}}\left( {\mathit{\boldsymbol{f}} - \mathit{\boldsymbol{v}}} \right)} \right]. $ |
其中, f是雾统计特征集合[13],v和Σ分别表示均值和d×d协方差矩阵,|Σ|和Σ-1是MVG密度模型协方差的行列式和逆矩阵,均值和协方差矩阵通过最大似然方法进行估计.
马氏距离的表达式为
| $ {\mathit{D}_f}\left( {{\mathit{\boldsymbol{v}}_1}, {\mathit{\boldsymbol{v}}_2}, {\sum _1}, {\sum _2}} \right) = \sqrt {{{\left( {{v_1} - {v_2}} \right)}^t}{{\left( {\frac{{{\sum _1} + {\sum _2}}}{2}} \right)}^{ - 1}}\left( {{v_1} - {v_2}} \right)} . $ |
其中,v1, v2和Σ1, Σ2是无雾图像集和测试图像集MVG模型的均值向量和协方差矩阵.同样,定义Dff为测试图像集和有雾图像集的在MVG模型中参数的距离.最后通过Df和Dff的比重来确定测试图像区域块雾浓度.
2 改进方法 2.1 大气光A的估计在He的论文中一般选取暗原色中最大亮度的前0.1%像素,并把它们对应到原始有雾图像中的相应像素点上,然后选定这些像素点中亮度最高像素点的值作为A值.也就是说,He选取了原始有雾图像I中的某一点的值作为整幅图像的大气环境光值,这样当图像中其他区域颜色偏亮时会很容易导致误选.为了使大气光的估计更可靠,本文基于天空区域像素值方差通常很低这个前提,采用四分搜索法将输入图像划分4个矩形区域,并定义每个区域取值为区域内所有像素值减去标准偏差的平均值,然后再选中具有最低取值的区域,并进一步将其划分成4个更小的区域.重复此过程,直到所选择的区域比预先规定的阈值小,将最后这块区域的像素亮度均值作为大气光取值.
2.1 大气光A的估计暗通道先验图像除雾的关键一步是投射图的计算.在He的文章中先通过暗通道先验粗估计投射图,然后利用软抠图或导向滤波进行细化,得到最终的投射图[9].
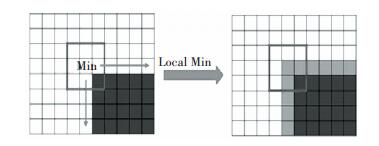
暗通道先验利用局部块最小操作来进行计算必然会产生“halo效应”.这是因为假如像素x位于边缘附件, 利用上述方法求取的最小值,在位置上会更倾向于边缘附近较暗的一面, 进而导致最终估计的值比实际值小.如图 3所示, 由于位于边缘附近较亮侧的像素会比整个亮区域有更低的极小值,而比整个暗区域会有较高的极小值,所以整个投射图边缘保持性并不是很好,在最终恢复的图像中边缘部分就会出现光带,即“halo效应”.
|
图 3 局部最小操作 Figure 3 The local minimum operation |
为了解决上述问题,提出一种更有效的方法来估算投射图.因为投射图与场景深度有关,而一个物体自身的像素具有相似的透射率.这就意味着透射率有局部不变性.对于一幅含雾图像I,首先计算每个像素点在各个通道中的最小值,记为I1(x).但是由于暗原色先验是基于局部最小值而不是一个像素点,所以不能直接用来估计投射图.因此本文首先计算不重叠块的暗通道先验值Bdark(i).然后利用周围块的加权插值方法来计算Idark(x),最后再利用导向滤波求取最终的透射图. Idark(x)的表达式为
| $ {I^{{\rm{dark}}}}\left( x \right) = \frac{1}{N}\left( {\lambda *{I^1}\left( x \right) + \sum\limits_{i \in s\left( x \right)} {{\omega _x}\left( i \right){B^{{\rm{dark}}}}\left( i \right)} } \right). $ | (2) |
其中,
ωx(i)计算公式为
| $ {\omega _{\rm{X}}}\left( i \right) = {{\rm{e}}^{ - {D_{\rm{X}}}{{\left( i \right)}^2}/{\sigma ^2}}}, $ |
其中DX(i)=I1(x)-Bdark(i),σ=0.3.
通过式(2)可知, 对于任一像素, 当I1(x)与邻域块的Bdark(i)差别很小时, 像素Idark(x)趋向于和块i来自于同一物体, 所以对应权重ωx(i)相应很高.而当I1(x)与邻域块的Bdark(i)差别很大时, 像素Idark(x)趋向于和块i来自于不同物体, 相应权重ωx(i)很低.一方面I1(x)的存在可以很好地保留细节信息, 另一方面通过加权归一化计算得到的值会更倾向于来自同一物体, 即满足局部不变特性.这样在边缘部分的求取中就不会发生求取的值倾向于边缘较暗的一面的问题, 所以该方法能够有效计算暗通道像素值,避免由于块效应而引起的“光晕效应”.
另外,在He的文章中对于无雾图像暗通道先验假设是Jdark→0,所以在后面的计算中舍弃Jdark(x)因子即将式(1)的值设置为0.在大多数情况下这项操作没有问题,但是在天空或接近大气光的明亮区域式,公式并不成立.所以在一些特殊情况下,会出现暗通道先验在天空等明亮区域失效的情况.
为了解决这个问题, 通过重新计算无雾图像的暗通道先验值Jdark(x)来进行校正.通过I1(x)对Jdark(x)进行拟合, 根据图 2和图 3可以知道,对于一幅无雾图像, 其像素分布可以用一个高斯模型来拟合, 通过一种自适应方法求取Jdark(x), 表达式为
| $ \frac{{{\mathit{\boldsymbol{J}}^{{\rm{dark}}}}\left( x \right)}}{\mathit{\boldsymbol{A}}} = {\omega _2}*{e^{\left( { - {{\left( {2.5 - {\mathit{\boldsymbol{I}}^{{\rm{dark}}}}\left( x \right)/\mathit{\boldsymbol{A}}} \right)}^2}/z} \right)}}, $ |
其中ω2和Z是为了调整模型形状和取值以自适应求取暗通道值而设立的, 本文实验调整为ω2=13,Z=0.65.
暗通道先验透射图的估计表达式为
| $ t\left( x \right) = \frac{{1 - {\mathit{I}^{{\rm{dark}}}}\left( x \right)/A}}{{1 - {\mathit{J}^{{\rm{dark}}}}\left( x \right)/A}}, $ |
综合以上,改进后的投射图估算公式为
| $ t\left( x \right) = \frac{{1 - {\omega _1}*{\mathit{I}^{{\rm{dark}}}}\left( x \right)/A}}{{1 - {\omega _2}*{e^{\left( { - {{\left( {2.5 - {\mathit{I}^{{\rm{dark}}}}\left( x \right)/\mathit{A}} \right)}^2}/z} \right)}}}}, $ |
其中在He等人[9]的文章中为了使图像更自然真实,设置ω1=0.95.
2.3 基于图像融合策略的信息增强通过上面处理得到的结果虽然消除了暗通道先验失效和“halo效应”,但是仍存在图像颜色偏暗、高雾浓度区域对比度低、信息特征少等问题,因此本文通过图像增强的方式利用融合策略来增加图像的有用信息.
图像I2是利用2.2节改进方法获取的图像,即消除了“halo效应”和暗通道先验失效后的图像.定义I1为白平衡图像,I3是通过雾浓度感知模型导出的图像,主要是为了补偿I2在浓度高区域的处理中缺失的特征信息和颜色偏移.其表达式为
| $ {I_3} = \gamma \left[{I-\mu \left( {{I_{{\rm{least\_foggy}}}}} \right)} \right]. $ |
在文献[13]中,为了增强图像细节信息和对比度,提出通过加权图融合来增强图像的信息和可见度.在融合过程中,为了保留更多显著特征,本文使用加权图进行计算.多尺度融合方法是基于人的视觉系统对局部变化敏感这一事实,并且多尺度融合提供了一种吸纳不同分辨率的图像局部细节的简便方法.每个预处理图像和相应的归一化权重图利用拉普拉斯金字塔和高斯金字塔进行分解.
| $ {F_l} = \sum {_k{G_l}\left\{ {{W^k}} \right\}{L_l}\left\{ {{I_k}} \right\}} . $ |
为了消除融合降质,在实验中取l=9为金字塔等级,Gl{·}和Ll{·}为金字塔等级l的高斯和拉普拉斯分解.操作通过自下而上的方式在每一层依次执行.最后,除雾图像通过拉普拉斯金字塔重建获得.
3 实验结果为了验证所提出的去雾方法的有效性, 利用多幅含雾图像对其进行测试,并且和He[9],Tarel[8],Fattal[7]和Lark[13]的方法进行比较.所有的算法都是在采用MATLABR2014a实现,实验系统环境是主频为3.4 GHz和4 GB RAM的PC.
3.1 现实世界图像的定性比较由于所有的去雾算法对一般室外图像能够得到非常好的结果,为了对它们进行比较,对一些具有白色或灰色区域的挑战性图像进行处理,因为大多数现有的去雾算法对白色是不敏感的.
在图 4中,Tarel[8]的结果对大多数的雾都能很好去除,对场景和对象的细节都能很好的恢复.然而在部分区域会出现过度增强现象,如在天空区域颜色会更暗.这是因为Tarel[8]的算法和He[9]的算法都具有过高估计透射率的问题.此外由于中值滤波中位数是边缘不保持性的滤波,所以在边缘区域会出现“halo效应”. Fattal[7]的方法在场景的天际线附近对雾只能进行部分除去,并且处理后的图像整体颜色也过饱和.这是由于Fattal[7]的算法是基于统计学的,需要充足的颜色信息以及差异性.当雾很浓时,颜色很微弱,差异也不够明显,他的评估透射率的方法就不可靠了. He[9]的结果虽然有更好的视觉效果,但不幸的是,当场景亮度和大气光相似时暗通道先验是无效的,在一些情况下透射率的估计是不可靠的,所以在天空区域和雾浓度高的情况下处理效果欠佳. Lark[13]的结果虽然得到很好的效果,但是在天空区域也会出现颜色偏暗和处理效果不佳等问题.与这4种方法相比,本文的方法不会出现过饱和现象,并且在天空等明亮区域能取得很好的处理效果.

|
图 4 去雾方法对比实验图像(图中从左至右依次原始有雾图像、Fattal、He、Lark、Tarel和本文方法的处理结果) Figure 4 Comparison of the recent dehazing techniques(besides the initial hazy images in this figure are displayed the results of Fattal, He, Lark, Tarel and our method) |
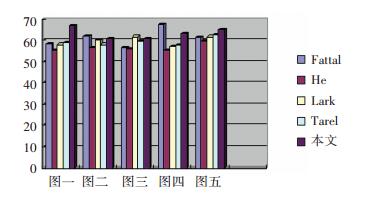
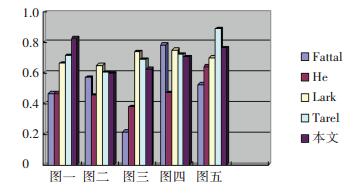
为了定量评估算法性能,计算各个算法结果的峰值信噪比(PSNR)和结构相似性(SSIM)来作为比较,对比结果如图 5和图 6所示.
|
图 5 算法的PSNR对比柱状图 Figure 5 PSNR's comparative histogram of the recent dehazing techniques |
|
图 6 算法的SSIM对比柱状图 Figure 6 SSIM's comparative histogram of the recent dehazing techniques |
峰值信噪比公式为
| $ PSNR = 10*lo{g_{10}}\left( {\frac{{{{\left( {{2^n} - 1} \right)}^2}}}{{{\rm{MSE}}}}} \right). $ |
其中n为采样值得比特数,此时值设为8.
MSE的计算公式为
| $ MSE = \sqrt {\frac{1}{{3N}}\sum\limits_{c \in \left\{ {r, g, b} \right\}} {{{\left\| {{J^c} - {G^c}} \right\|}^2}} } . $ |
峰值信噪比(PSNR)是最普遍最广泛使用的评鉴画质的客观量测法,其值越大,就代表失真越少.结构相似性(SSIM)是用来评估算法保留结构信息的能力.其值越大越好,最大为1.从表 1数据可以看出,本文方法整体PSNR值比其他算法的值都较高,说明方法失真较少.而SSIM的值处于中等程度,说明该算法也能很好地保留更多的结构化信息.
4 结论本文结合改进的自适应暗通道先验算法和图像融合策略对单幅图像进行处理,不仅保留了暗通道先验简单有效的优势,而且还针对处理结果中出现的“halo效应”和暗通道先验在天空等明亮区域失效的情况进行了提升.通过图像融合解决图像整体颜色偏暗的问题和增强了高浓度雾区域的特征信息.实验表明,该方法在图像可见度和处理效果上有所改善,尤其在天空等明亮区域的处理效果有了显著提高.
| [1] | NARASIMHAN S G, NAYAR S K. Contrast restoration of weather degraded images[J]. IEEE Trans. Pattern Anal. Mach. Intell,2003, 25 (6) : 713-724. DOI: 10.1109/TPAMI.2003.1201821 |
| [2] | CHAVEZ P S. An improved dark-object subtraction technique for atmospheric scattering correction of multispectral data[J]. Remote Sens. Environ,1988, 24 (3) : 459-479. DOI: 10.1016/0034-4257(88)90019-3 |
| [3] | HAUTIERE N, TAREL J P, LAVENANT J, et al. Automatic fog detection and estimation of visibility distance through use of an onboard camera[J]. Machine Vision and Applications,2006, 17 (1) : 8-20. DOI: 10.1007/s00138-005-0011-1 |
| [4] | KOPF J, NEUBERT B, CHEN B, et al. Deep photo: model-based photograph enhancement and viewing[C]//ACM Transactions on Graphics (TOG). New York:ACM, 2008, 27(5): 116. |
| [5] | KOSCHMIEDER E L. Bénard convection[J]. Adv. Chem. Phys,1974, 26 (177-212) : 605. |
| [6] | TAN R T. Visibility in bad weather from a single image[C]// IEEE Conference on Computer Vision and Pattern Recognition. Anchorage: IEEE, 2008: 1-8. http://www.oalib.com/references/17176576 |
| [7] | FATTAL R. Single image dehazing[J]. ACM transactions on graphics,2008, 27 (3) : 72. |
| [8] | TAREL J P, HAUTIERE N. Fast visibility restoration from a single color or gray level image[C]// IEEE 12th International Conference on Computer Vision. IEEE, 2009: 2201-2208. |
| [9] | HE K, SUN J, TANG X. Single image haze removal using dark channel prior[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence,2011, 33 (12) : 2341-2353. DOI: 10.1109/TPAMI.2010.168 |
| [10] | HE K, SUN J, TANG X. Guided image filtering[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence,2013, 35 (6) : 1397-1409. DOI: 10.1109/TPAMI.2012.213 |
| [11] | ANCUTI C O, ANCUTI C. Single image dehazing by multi-scale fusion[J]. IEEE Trans. Image Process.,2013, 22 (8) : 3271-3282. DOI: 10.1109/TIP.2013.2262284 |
| [12] | CHOI L K, YOU J, BOVIK A C. Referenceless perceptual fog density prediction model[J]. Proc. SPIE,2014, 9014 (10) : 90140H. |
| [13] | CHOI L K, YOU J, BOVIK A C. Referenceless prediction of perceptual fog density and perceptual image defogging[J]. IEEE Transactions on Image Processing,2015, 24 (11) : 3888-3901. DOI: 10.1109/TIP.2015.2456502 |
 2016, Vol. 48
2016, Vol. 48


