网络聚簇结构是复杂网络的重要特征之一,网络聚簇结构特征表明社区结构存在于复杂网络中.社区,即其内部节点之间关系相对紧密、内部节点与外部节点关系相对稀疏的节点集合.通过分析复杂网络的结构特征,挖掘复杂网络中的社区结构,这个过程就是社区发现.起初,研究人员利用图论和概率统计相关理论挖掘网络的本质和特点.随着互联网的信息爆炸和人们沟通方式的转变,复杂网络的数据规模越来越大,快速、有效的社区发现方法成为多领域研究的热点问题之一[1].研究复杂网络社区发现方法对分析复杂网络的拓扑结构和层次结构、理解社区的形成过程、预测复杂网络的动态变化、发现复杂网络中蕴含的规律特征具有重要意义, 在众多领域有广泛的应用前景[2-5].
1970年,Kernighan和Lin基于贪婪算法提出了Kernighan-Lin方法[6],用于将网络划分为两个规模确定的社区.该方法需要预先设定社区规模等较多先验知识,在实际网络中应用有限. GN算法[7]是社区发现经典方法之一,由Girvan和Newman于2001年提出.该方法核心思想为社区内的边介数应小于社区间的边介数. GN算法时间复杂度较高,为O(m2n),其中,m表示网络中边的数量,n表示网络中的节点数. Newman等提出模块度[8]作为衡量社区发现结果质量优劣的标准. Palla等[4, 9-10]首次针对重叠社区提出了极大团过滤社区发现方法.该方法需要事先确定参数,不同的参数值使得社区发现结果差异较大.
针对上述传统方法参数难以确定、算法复杂度高的不足,Zhu等[11]提出了标签传播算法LPA(label propagation algorithm).由于LPA方法时间复杂度低且效果好,研究人员对其进行了大量深入研究. Raghavan等[12]首次将LPA方法用于复杂网络中的社区发现,提出了RAK方法.该方法首先将网络中每个节点赋予一个唯一的标签,然后根据当前节点的邻接点标签分布情况更新当前节点的标签,重复上述过程直到每个节点的标签都与其邻接点最多的标签相同,标签相同的节点划分为同一个社区. RAK方法节点初始化标签时间复杂度为O(n),每次标签传播的时间复杂度为O(m).此外,RAK方法无需社区数量、社区规模等先验知识,仅根据网络自身结构发现社区,因此RAK方法对网络结构有很好的适应性.
为了提高RAK方法社区发现的性能,许多研究人员做出很多尝试[13-23]. Barber等[13]提出了一种模块化标签传播算法,定义目标函数H,将社区发现映射到最优化目标函数H,避免整个网络仅为一个社区的情况;Cordasco等[14]提出了一种基于半同步标签传播过程的方法,标签传播过程是并行的,从而提高了RAK方法社区发现的计算速度;Leung等[15]提出了一种扩展的RAK方法用于实时社区监测,通过设定参数,使得算法具有扩展性,提高了RAK方法的计算速度.为降低RAK方法的随机性,Zhao等[16]提出了基于标签的熵的标签传播方法LPA-E(label propagation in entropic order),将节点按照标签的熵从小到大排序进行标签传播;康旭彬等[17]提出了基于节点相似度的标签传播算法;Sun等[18]提出了利用邻接点影响力确定标签传播顺序的方法.尽管上述方法一定程度上提高了标签传播社区发现方法的性能和稳定性,但都是仅从一个方面进行改进,且改进的方面完全消除了随机性,不能体现RAK方法的仅依据网络自身结构发现社区的特点.
本文提出一种稳定的标签传播社区发现方法,既保留了RAK方法无需先验知识等优点,又提高了标签传播社区发现结果的质量和稳定性.首先通过网络中不重叠三角形进行标签初始化,然后根据节点标签计算得到的熵确定随机队列,最后考虑邻接点的邻接点标签分布情况确定传播标签.
1 稳定标签传播的社区发现方法为提高标签传播社区发现方法的稳定性,本文在RAK方法的标签初始化、随机队列设置和标签传播过程分别进行了改进.在标签初始化中,发现网络中所有不重叠三角形,给予三角形三个节点相同的标签,每个三角形标签各不相同,剩余节点赋予其他不同标签;在随机队列设置上,先将节点标签计算得到的熵从小到大对节点排序,再在排序基础上分三段随机排序;针对标签传播的随机选择,考虑被传播节点邻接点的邻接点标签与邻接点标签相同的概率,选择概率大的标签确定传播标签选择.
1.1 不重叠三角形标签初始化RAK方法中,每个节点的初始化标签是各不相同的,本文提出了一种无重叠三角形标签初始化方法,用来减少初始标签数量.网络中,有很多联系紧密具有团体性的节点簇,如极大团,节点簇往往属于同一社区,且易成为社区的核心部分. CPM算法中[4],极大团往往作为社区的核心部分,进行社区发现.社区核心部分的确定,社区发现的结果也将更加稳定.
基于网络和社区的这个特点,在标签初始化前,首先找出网络中所有极大团,赋予每个极大团内节点相同的标签.然而,发现网路中所有极大团是NP完全问题,算法的时间复杂度较高,发现所有极大团所耗时间远远超过标签传播整个算法的时间.因此,本文提出了采用发现网络中没有节点重叠的不重叠三角形的方法,赋予发现到的三角形节点相同的标签,进行网络节点标签初始化,如算法1所示.
算法1不重叠三角形标签初始化方法伪代码
输入:邻接矩阵AdjacentMatrix,节点个数VerticeNum,节点邻居集合Neighbor.
输出:标签数组Community.
for i←to VerticeNum Do
isVisited[i]←False;
c=0;
for i←0 to VerticeNum Do
for j←0 to Neighbor[i].size Do
for k←0 to Neighbor[j].size Do
if AdjacentMatrix[k][i]=1 and isVisited[i\j\k]=False then
Community[i\j\k]←c;
isVisited[i\j\k]←True;
c++;
for i←to VerticeNum Do
if isVisited[i]←False;
Community[i]←c;
isVisited[i]←True;
return Community;
如图 1所示,节点v1,v2和v3组成一个三角形,初始化标签均为l1,其他不能组成三角形的节点分别赋予不同的标签.
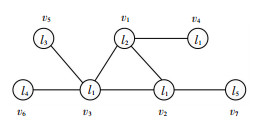
|
图 1 不重叠三角形标签初始化 Figure 1 Label initialization on non-overlapping triangles |
不重叠三角形标签方法的时间复杂度为O(n2),比RAK方法的近似线性时间复杂度有所提升,但减少了初始标签的数量.其原因是RAK方法初始标签数量等于节点数量,而不重叠三角形的3个节点被赋予相同的标签,因此,初始标签数量要少于节点数量,即少于RAK方法的初始标签数量.
1.2 基于节点标签的熵的随机队列分析随机队列对社区发现结果稳定性的影响,考虑图 2所示网络,6个节点v1,v2,v3,v4,v5,v6,初始化标签分别为l1,l2,l3,l4,l5,l6.从直观角度看,节点v1,v2和v3构成一个社区,节点v4,v5和v6构成另一个社区.若v1最先进行标签更新,选择的标签可能为l2或l3.接下来无论v2还是v3先更新标签,v1,v2,v3都能被划分到同一个社区.若v5或v6先进行标签更新,或v4标签更新的时候不选择l3,则v4,v5,v6将被划分到另外一个社区.如果v3最先更新标签,则可能为l1,l2或l4.若为l1或l2,则结果与上述分析一样;若为l4,则6个节点可能划分为一个社区.因此,降低随机队列的随机性将提高社区发现结果的稳定性.
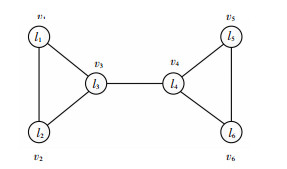
|
图 2 6个节点的网络 Figure 2 Network with 6 nodes |
为降低随机队列的随机性,本文首先采用了文献[16]的方法,利用节点标签计算得到的熵的大小对节点进行先后排序.节点标签计算得到的熵公式为
| $ {H_v} =-\sum\limits_{l \in L\left( {v, N\left( v \right)} \right)} {p\left( l \right)\log p\left( l \right)} . $ |
式中:L(v, N(v))为节点v和其邻居节点的标签集合;p(l)为标签l在L(v, N(v))中的概率,即在节点v和N(v)中,标签为l的节点数与节点v及其邻接点N(v)节点数的比.具体算法如算法2所示.
算法2基于节点标签的熵的随机队列方法伪代码
输入:邻接矩阵AdjacentMatrix,节点个数VerticeNum,标签数组Community.
输出:基于节点标签的熵的随机队列Ssort.
for i←0 to VerticeNum Do
FindNeighbor(i, AdjacentMatrix, NeighBor)
for j←0 to Neighbor.size Do
labelNum[Community[Neighbor[j]]]++;
for k←0 to Neighbor.size Do
pl←labelNum[k]/(Neighbor.size()+1.0);
Ssort[i].S +=-pl*log(pl);
qsort(Ssort)
RandomSort(Ssort, VerticeNum/3);
RandomSort(Ssort+VerticeNum/3, VerticeNum/3*2);
RandomSort(Ssort+(VerticeNum/3)*2, VerticeNum);
return Ssort;
这种排序方法消除了传播节点队列的随机性,使结果变得确定,标签传播方法的适应性大幅度降低.为了保证标签传播算法的适应性,本文提出将这种方法排序好的队列平均分成三个部分,每个部分内节点进行随机排列.这样既降低了算法的随机性,又未彻底消除算法随机性,保持了标签传播算法仅依靠网络本身连接结构进行社区发现的初衷.
1.3 基于邻接点的邻接点标签分布的标签选择标签传播过程中,当遇到最多数量的相同标签不唯一时,RAK方法采用随机的方式进行选择,这使得最终社区发现结果随机性较大.为降低标签传播过程中的随机性,本文提出根据被传播节点邻接点的邻接点集标签分布情况,进行标签选择的方法,如算法3所示.
v为当前被传播节点,K为N(v)中相同标签数量最多的节点集合,klK, kl为标签是l的节点集合.考虑N(kl)中标签与标签l相同的节点所占比例,选择比例最大的那个标签,作为节点v新的标签.如果比例相同,则随机选择一个.
算法3基于邻接点的邻接点标签分布的标签传播方法伪代码
输入:邻接矩阵AdjacentMatrix,节点个数VerticeNum.
输出:传播后的标签数组Community.
for i←0 to VerticeNum Do
VectorFrequency(Neighbor[i], label);
if label.size()=1 then
Community[i]←label[0];
else then
for j←0 to label.size Do
LabelFrequency(label[j], freqmax);
if freqmax.size=1 then
Community[i]←freqmax[0].label;
else then
Community[i]←freqmax[random].label;
return Community;
考虑邻接点的邻接点标签分布情况,相当于给邻接点标签加上了一个权重.如果权重值高,则说明该邻接点的标签背后有更多的支撑,邻接点的标签具有更强的影响力,应该选择该权重值高的邻接点标签.这使得原来的标签随机性选择变成确定性选择,从而提高了社区发现结果的稳定性.同时,在权重值相同的情况下,保留了标签选择的随机性,保持了RAK方法的适应性.
2 实验及分析 2.1 实验数据选择了Zachary’s Karate Club[24]、Dolphin Social Network[25]和American College Football [7](简称Karate、Dolphins和Football网络)这3个被广泛使用的社会网络进行测试,网络具体数据如表 1所示.
| 表 1 实验网络的基本数据 Table 1 Basic data of test networks |
实验环境为intel(R) Core(TM) i5 CPU M 430 @2.27GHz, 2.27GHz, 4GB, Windows 7操作系统.
2.2 实验评测方法采用文献[12]提出的fsame函数和Jjaccard’s index函数作为衡量不同社区相似度标准,将本文方法与RAK方法和LPA-E方法进行比较. fsame函数用于比较两个社区发现结果的相似度,计算公式为
| $ {f_{{\rm{same}}}} = \frac{1}{2}\left( {\sum\limits_i {{{\max }_j}\left\{ {{M_{ij}}} \right\}} + \sum\limits_j {{{\max }_i}\left\{ {{M_{ij}}} \right\}} } \right)\frac{{100}}{n}. $ |
式中Mij表示在一个社区发现结果中社区i和在另一个社区发现结果中社区j相同节点的个数. fsame函数对在一个社区发现结果中几个小的社区在另一个社区发现结果中合并成一个大的社区这种情况不是很敏感.因此,还用到了Jjaccard’s index函数,计算公式为
| $ {J_{{\rm{jaccard's}}\;{\rm{index}}}} = \frac{a}{{a + b + c}}. $ |
式中:a是在两次发现结果中都在同一个社区的节点对数量,b是第一次在同一个社区而第二次在不同社区的节点对数量,c是第一次在不同社区而第二次在同一社区的节点对数量. Jjaccard’s index函数值越大,表明两种社区发现结果越相近.
为评测社区发现结果的质量,采用了Newman等提出的模块度[8]作为评价标准. Newman等认为,复杂网络社区最优发现结果并不代表社区间的边数在绝对数量最少,而是比期望边数少.模块度定义为社区内的边数减去随机生成图中的期望边数,形式化定义如下:网络划分为k个社区,k*k的矩阵E=(eij),eij表示网络中社区i与社区j之间的边数占所有边数的比例;矩阵的迹
| $ Q = \sum\limits_i {\left( {{e_{ij}}-a_i^2} \right)} = {\rm{Tr}}\left( \boldsymbol{E} \right)-\left\| {{\boldsymbol{E}^2}} \right\|, $ |
式中‖X‖为所有x元素之和.
2.3 实验结果与分析在Karate、Dolphins和Football网络上对本文方法、RAK方法和LPA-E方法进行测试,选择5个社区发现结果进行两两比较.实验结果如表 2~4所示,表中右上半部分为fsame函数值,左下半部分为Jjaccard’s index函数值.
| 表 2 RAK方法、LPA-E方法和本文方法在Karate网络上社区发现结果比较 Table 2 Comparison of the results in Karate network among RAK, LPA-E and our method |
| 表 3 RAK方法、LPA-E方法和本文方法在Dolphins网络上社区发现结果比较 Table 3 Comparison of the results in Dolphins network among RAK, LPA-E and our method |
| 表 4 RAK方法、LPA-E方法和本文方法在Football网络上社区发现结果比较 Table 4 Comparison of the results in Football network among RAK, LPA-E and our method |
从表 2~4实验结果看,LPA-E方法和本文方法的fsame函数值和Jjaccard’s index函数值均高于RAK方法,表明两种方法都提升了社区发现稳定性.在规模较小的Karate网络中,随着算法随机性的下降,经常会出现社区发现结果完全一致的情况,如表 2中LPA-E方法和本文方法左下角数值为1.000.
为从整体上比较三种方法的稳定性,对Karate、Dolphins和Football网络分别用RAK方法、LPA-E方法和本文方法进行100次社区发现,计算两两结果Jjaccard’s index函数值的平均值,如表 5所示.
| 表 5 100次社区发现结果相互之间的jaccard’s index函数平均值 Table 5 Average value of jaccard's index with 100 trails |
在Dophins和Football网络中,本文方法的Jjaccard’s index函数值平均值最高;在Karate网络中,LPA-E方法的Jjaccard’s index函数值平均值最高.为了分析造成这种结果的原因,统计了初始化时不重叠三角形个数F1和标签传播时遇到邻接点最多数量标签不唯一的次数F2,用来分析本文1.1节中改进方法和1.3节中改进方法在不同网络中的影响力,如表 6所示.
| 表 6 100次社区发现中不重叠三角形个数和标签传播时邻接点最多数量标签不唯一次数的平均值 Table 6 Average value of non-overlapping triangles and number of maximum label not unique with 100 trials |
从表 6数据可知,Karate网络中的不重叠三角形个数和标签传播时遇到邻接点最多数量标签不唯一的次数都要少于Dophins和Football网络中的个数和次数,这表明本文1.1节中改进方法和1.3节中改进方法在Karate网络中的影响力低于在Dophins和Football网络中的影响力. 表 5 Karate结果中,本文方法结果低于LPA-E方法结果,是由于本文1.1节中改进方法和1.3节中改进方法所提高的稳定性不足以抵消1.2节中改进方法里保留的随机性,这主要是由网络规模决定的,网络规模越大,网络中的不重叠三角形数量越多,发生标签传播时邻接点最多数量标签不唯一的情况越多.虽然本文方法的Jjaccard’s index函数平均值略低于LPA-E方法,但远高于RAK方法,说明本文方法较好地提高了社区发现结果稳定性,同时也验证了本文方法没有完全消除RAK方法的随机性,保留了RAK方法对网络本身结构适应性的优点.
对Karate、Dolphins和Football网络分别用RAK方法、LPA-E方法和本文方法进行100次社区发现,并计算社区发现结果的Q函数平均值,结果如表 7所示.
| 表 7 100次社区发现结果的Q函数平均值 Table 7 Average value of Q function of community discovery with 100 trails |
Q函数表示的是社区内边数与随机生成图中期望边数的差,反映了社区内部紧密程度,Q函数值越大,表明发现的社区结构越紧密,越符合社区的定义,社区发现结果质量越好.实验结果表明,本文方法的Q函数平均值高于RAK方法和LPA-E方法,提升了社区发现质量.
实验表明,本文算法较好地提升了标签传播算法的稳定性和社区发现结果质量.
3 结论1)改进了RAK方法标签初始化过程,通过挖掘网络中的不重叠三角形,赋予三角形节点相同的标签,减少了初始化标签数量;
2)降低且未完全消除方法的随机性,采用节点标签计算得到的熵和邻接点的邻接点标签分布情况进行标签传播选择,提高了社区发现结果的稳定性,同时保持了标签传播方法的无需先验知识,仅依靠网络结构本身的特点.
3)本文改进的算法较好地提高了标签传播社区发现结果的质量和稳定性.
| [1] | ADAMIC L A, HUBERMAN B A, BARAB SI A L, et al. Power-law distribution of the world wide web[J]. Science,2000, 287 (287) : 2115a-2115a. DOI: 10.1126/science.287.5461.2115a |
| [2] | SIDIROPOULOS A, PALLIS G, KATSAROS D, et al. Prefetching in content distribution networks via web communities identification and outsourcing[J]. World Wide Web-internet & Web Information Systems,2008, 11 (1) : 39-70. DOI: 10.1007/s11280-007-0027-8 |
| [3] | WANG Zhi, ZHANG Jianzhi. In search of the biological significance of modular structures in protein networks[J]. Plos Computational Biology,2007, 3 (6) : 1011-1021. DOI: 10.1371/journal.pcbi.0030107 |
| [4] | PALLA G, DERENYI I, FARKAS I, et al. Uncovering the overlapping community structure of complex networks in nature and society[J]. Nature,2005, 435 (7043) : 814-818. DOI: 10.1038/nature03607 |
| [5] | LI Xin, LIU Bing, YU P S. Discovering overlapping communities of named entities[J]. Lecture Notes in Computer Science,2006, 4213 : 593-600. DOI: 10.1007/11871637_60 |
| [6] | KERNIGHAN B W, LIN S. An efficient heuristic procedure for partitioning graphs[J]. Bell System Technical Journal,1970, 49 (2) : 291-307. DOI: 10.1002/j.1538-7305.1970.tb01770.x |
| [7] | GIRVAN M, NEWMAN M E J. Community structure in social and biological networks[J]. Proceedings of the National Academy of Sciences of the United States of America,2002, 99 (12) : 7821-7826. DOI: 10.1073/pnas.122653799 |
| [8] | NEWMAN M E J, GIRVAN M. Finding and evaluating community structure in networks[J]. Physical Review E Statistical Nonlinear & Soft Matter Physics,2004, 69 (2 Pt 2) : 026113-026113. DOI: 10.1103/PhysRevE.69.026113 |
| [9] | DERENYI I, PALLA G, VICSEK T. Clique percolation in random networks[J]. Physical Review Letters,2005, 94 (16) : 160202-160202. DOI: 10.1103/PhysRevLett.94.160202 |
| [10] | PALLA G, FARKAS I J, POLLNER P, et al. Directed network modules[J]. New Journal of Physics,2007, 9 (26) : 186-206. DOI: 10.1088/1367-2630/9/6/186 |
| [11] | ZHU X, GHAHRAMANI Z. Learning from labeled and unlabeled data with label propagation: Technical Report CMUCALD-02-107 [R]. Pittsburgh PA: Carnegie Mellon University, 2002. |
| [12] | RAGHAVAN U N, ALBERT R, KUMARA S. Near linear time algorithm to detect community structures in large-scale networks[J]. Physical Review E Statistical Nonlinear & Soft Matter Physics,2007, 76 (3 Pt 2) . DOI: 10.1103/PhysRevE.76.036106 |
| [13] | BARBER M J, CLARK J W. Detecting network communities by propagating labels under constraints[J]. Physical Review E Statistical Nonlinear & Soft Matter Physics,2009, 80 (2 Pt 2) : 283-289. DOI: 10.1103/PhysRevE.80.026129 |
| [14] | CORDASCO G, GARGANO L. Community detection via semi-synchronous label propagation algori-thms[C]// 2010 IEEE International Workshop on Business Applications of Social Network Analysis(BASNA). Bangalore: IEEE, 2010:1-8. |
| [15] | Leung I X Y, PAN Hui, LIO P, et al. Towards real-time community detection in large networks[J]. Physical Review E,2009, 79 (6) : 853-857. DOI: 10.1103/PhysRevE.79.066107 |
| [16] | ZHAO Yuxin, LI Shenghong, CHEN Xiuzhen. Community detection using label propagation in entropic order[C]// 2012 IEEE 12th International Conference on Computer and Information Technology (CIT). Si Chuan: IEEE, 2012: 18-24. |
| [17] |
康旭彬, 贾彩燕. 一种改进的标签传播快速社区发现方法[J].
合肥工业大学学报(自然科学版),2013, 36 (1) : 43-47.
KANG XUBIN, JIA CAIYAN. An improved fast community detection algorithm based on label propagation[J]. Journal of HeFei University of technology,2013, 36 (1) : 43-47. DOI: 10.3969/j.issn.1003-5060.2013.01.010 |
| [18] | SUN Heli, HUANG Jianbin, ZHONG Xiang, et al. Label propagation with α-degree neighborhood impact for network community detection[J]. Computational Intelligence & Neuroscience,2014 (2014) : 130689-130689. DOI: 10.1155/2014/130689 |
| [19] | XING Yan, MENG Fanrong, ZHOU Yong, et al. A node influence based label propagation algorithm for community detection in networks[J]. Scientific World Journal,2014, 2014 (3) : 627581-627581. DOI: 10.1155/2014/627581 |
| [20] | SUN Heli, LIU Jiao, HUANG Jianbin, et al. CenLP: a centrality-based label propagation algorithm for community detection in networks[J]. Physica A Statistical Mechanics & Its Applications,2015, 436 : 767-780. DOI: 10.1016/j.physa.2015.05.080 |
| [21] | HOSSEINI R, AZMI R. Memory-based label propagation algorithm for community detection in social networks[C]// 2015 International Symposium on Artificial Intelligence and Signal Processing (AISP). Mashhad : IEEE, 2015:256-260. |
| [22] | DICKINSON B, HU Wei. The effects of centrality ordering in label propagation for community detection[J]. Social Networking,2015, 4 (4) : 103-111. DOI: 10.4236/sn.2015.44012 |
| [23] | ZHANG Xiankun, TIAN Xue, LI Yanan, et al. Label propagation algorithm based on edge clustering coefficient for community detection in complex networks[J]. International Journal of Modern Physics B,2014, 28 (30) : 1450216-1450216. DOI: 10.1142/S0217979214502166 |
| [24] | ZACHARY W W. An Information flow model for conflict and fission in small groups[J]. Journal of Anthropological Research,1977, 33 (4) : 452-473. DOI: 10.1086/jar.33.4.3629752 |
| [25] | LUSSEAU D, SCHNEIDER K, BOISSEAU O J, et al. The bottlenose dolphin community of doubtful sound features a large proportion of long-lasting associations[J]. Behavioral Ecology & Sociobiology,2003, 54 (4) : 396-405. DOI: 10.1007/s00265-003-0651-y |
 2016, Vol. 48
2016, Vol. 48


