2. 中建八局大连公司, 辽宁 大连 116021 ;
3. 诺基亚通信系统技术(北京)有限公司浙江分公司, 杭州 310053
2. Dalian Branch China Construction Eighth Engineering Division Corp. Ltd, Dalian 116021, Liaoning, China ;
3. Nokia Solutions and Networks, Hangzhou 310053, China
学习矢量量化LVQ (learning vector quantization)是一种适用于大规模、大类别分类任务的原型学习算法,具有低存储、高识别吞吐率的优点.已有的研究表明,当采用判别学习准则时,原型学习能在数字识别、汉字识别(含日本文字识别)问题上获得较先进的识别结果[1]. LVQ同样在选取有限候选类方面具有非常好的效果.例如,LVQ可以用来为复杂模型筛选小部分有潜力的类别集,从而有效缓解PL-MQDF模型[2]的高强度训练过程.更重要的是,随着移动设备的普及,LVQ以其模型精巧、速度快等特点能很好地适用于智能手机、平板电脑等嵌入式设备上的输入法应用[3-4].
学习一个鲁棒的大规模LVQ模型,其计算复杂性令人望而生畏.若使用单核CPU的传统实现方法,将需要若干天的训练时间.而对于判别学习准则来说,数据越多识别效果则越好,当然学习时间会相应的加长.部分研究者尝试通过收集或人工合成的方式获取更多的训练样本.最新的一些研究结果认为,当指数级增长样本数量时,识别效果可以得到稳步提升[5-6].然而,目前已进入了多核计算时代.英特尔公司的Pat Gelsinger曾表示,若芯片仍按照传统方式设计,到2015年芯片将如同太阳表面一样热[7]. GPU所使用的异构并行计算架构已开始逐渐补充甚至部分代替传统的串行计算架构.因此,从单核处理器转向大规模并行处理器是未来算法设计的必然趋势.
GPU异构计算架构在机器学习以及模式识别任务领域具有突出的加速效果. Raina等人研究了深度信念网络DBN (deep belief network)与稀疏编码在GPU上的实现[8],他们的DBN实现方案达到了70倍的加速比,而稀疏编码的并行算法则获得了5到15倍的加速比.一些学者也研究了大型多层神经网络在GPU上的实现. Scherer与Behnke[9]在GPU上实现了加速比达100倍的卷积神经网络CNN (convolution neural network). Ciresan等人则在GPU上实现了深度多层感知机,并且取得了当前最好的识别性能[10].周明可等人则针对改进二次判别函数MQDF (modified quadratic discriminative function)实现了基于GPU的判别训练方法,并将其成功应用到了汉字识别上,其小批量处理实现方案获得了15倍的加速比[6].
本文提出一种适用于大规模、大类别分类任务的异构原型学习算法框架.与已有的研究工作不同,本文提出的框架几乎将所有的计算负载都调度到GPU上,CPU只负责协调部分计算逻辑.为了充分利用GPU的计算资源,算法深入分析了计算负载的可并行度,大量使用了分块平铺以及并行归约等并行计算模式.算法在大类别手写汉字识别任务下进行验证,得到比较高的可扩展性.在小批量处理的模式下,使用消费级显卡GTX680,该算法最高可达194倍的加速比.当升级到新一代GTX980时,加速比提升到638倍.最值得一提的是,该算法在随机梯度模式下也可以获得至少30倍的加速比.
1 算法 1.1 LVQ串行算法假设有一个包含C个类别的分类任务,原型学习即产生一个原型向量集Θ={mi, i=1, 2, …, C}.为便于讨论,本文的形式化主要对每个类包含一个原型(类中心)的情况展开,所述框架同样适用于每个类包含多个原型的情况.预测未知标号样本x的标记问题,可以转化为查找最小距离问题.计算x与每个原型向量的欧氏距离,通过查找C个距离的最小值,就可以把x的标号设为拥有最小距离的原型向量所在类别,表示x与该类别的原型最相似.该预测过程可形式化为把x赋予标号j:
| $ j = \mathop {\arg \min }\limits_i {\left\| {x-{m_i}} \right\|_2}. $ |
为了学习一个原型向量集,需要从大规模训练样本中进行有监督的训练.用{(xn, yn), n=1, 2, …, N }表示训练样本集,其中yn为样本xn的真实标号,整个训练过程的目标就是针对训练集最小化经验损失[11]:
| $ \mathit{\boldsymbol{ \boldsymbol{\hat{\varTheta}} = }}\mathop {\arg \min }\limits_\mathit{\Theta } \frac{1}{N}\sum\limits_{n = 1}^n {\varphi \left( {f\left( {{x_n},\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}} \right)} \right)} , $ | (1) |
其中φ(·)为针对评分函数f(x, Θ)的损失函数.
为了求解式(1)中的最小化问题,通常采用随机梯度下降SGD (stochastic gradient descent)的方法对参数进行更新:
| $ \mathit{\boldsymbol{ \boldsymbol{\varTheta} }}\left( {t + 1} \right) = \mathit{\boldsymbol{ \boldsymbol{\varTheta} }}\left( t \right) - \eta {\nabla _\mathit{\Theta }}\varphi \left( {f\left( x \right)} \right)\left| {_{x = {x_n}}} \right., $ |
其中η表示学习步长.
为说明LVQ中的判别学习思想,此处以广义学习矢量量化GLVQ (generalized learning vector quantization)为例.首先需定义一个可以度量样本x误差的测量函数:
| $ f\left( x \right) = \frac{{{d_c}-{d_r}}}{{{d_c}-{d_r}}}, $ | (2) |
这里dc与dr分别表示样本x与真实类别c以及竞争类别r之间的距离.分类损失函数可以通过sigmoid函数近似:
| $ \varphi \left( {f\left( x \right)} \right) = \frac{1}{{1 + {{\rm{e}}^{-\xi f\left( x \right)}}}}, $ | (3) |
其中ξ用来调节sigmoid函数的平滑度.
若使用欧氏平方距离,则mc与mr的更新公式可以表示为x的下列函数:
| $ \left\{ {\begin{array}{*{20}{l}} {{m_c} \leftarrow {m_c} + \eta f\left( x \right)\left( {1-f\left( x \right)} \right)\frac{{{d_r}}}{{{{\left( {{d_c} + {d_r}} \right)}^2}}}\left( {x-{m_c}} \right), }\\ {{m_r} \leftarrow {m_r}-\eta f\left( x \right)\left( {1 - f\left( x \right)} \right)\frac{{{d_c}}}{{{{\left( {{d_c} - {d_r}} \right)}^2}}}\left( {x - {m_r}} \right).} \end{array}} \right. $ | (4) |
整个GLVQ学习算法可由算法1中的伪码表示.算法1主要重复执行下列任务:采样一个样本,计算出该样本与所有原型之间的距离,获得真实类别与竞争类别,计算损失函数以及梯度,最后更新原型向量.
算法1 GLVQ学习算法(串行版本)
Input:training set{xn, yn}n=1, …, N, initial prototypes {mi}i=1, …, C
Output: {mi}i=1, …, C
1: while not convergent do
2: for each {xn, yn}
3: find out (mc, dc) and (mr, dr) through compare-then-exchange distances
4: compute error measure f(x) using Eq.(2)
5: derive loss function ϕ(x) using Eq.(3)
6: update mc and mr using Eq.(4)
7: end for
8: end while
9: return {mi}i=1, …, C
1.2 并行原型学习框架算法1的整体处理流程是一个串行过程.为了将其扩展到异构并行计算框架,采用带小批量处理(数量为mb)的梯度下降算法.改进的算法框架如算法2所示,其中的每个计算步骤(第3到6行)都可以并行执行.本框架不是一个接着一个的逐一计算每个样本与每个原型的距离,而是一次性计算一个批次的样本与全部原型的距离,保存为距离矩阵(见算法2第3行);与距离矩阵有关的计算涉及高密度的计算,具有较高的可扩展性.对于查找真实类别与竞争类别可以与计算分类损失函数合并进行,需要考察不同的并行执行备选方案(见算法2第4和5行).最后执行的参数更新操作,由于是针对一批样本的计算,再加上每个样本包含数百维特征,所以具有天然的并行性.
算法2 GLVQ学习算法(并行框架)
Input:training set{xn, yn}n=1, …, N, initial prototypes {mi}i=1, …, C
Output: {mi}i=1, …, C
1: while not convergent do
2: for each mini-batch Ti={(xi1, yi1), …, (xiM, yiM)}
3: compute all distances as a matrix in parallel
4: find out genuine/rival pair in parallel
5: derive loss functionin parallel
6: update prototypesin parallel
7: end for
8: end while
9: return {mi}i=1, …, C
本文中的GPU程序设计围绕英伟达公司的计算统一设备架构CUDA(compute unified device architecture)编程模型展开. GPU硬件从物理上提供了两个层面的并行模式:一块GPU上包含多个流多处理器SM (streaming multiprocessor),每个流多处理器上又包含若干个流处理器(或称为CUDA核心).代码的最终物理执行在SP上,CUDA核函数将计算封装然后分配到GPU上执行.逻辑上,CUDA也包含两个软件抽象层与两个物理层相对应,即线程块与线程,一个线程块由一组线程组成,线程块调度到SM上执行,线程块中的每个线程再具体调度到SP上执行.
同一线程块上的所有线程可以对一小块称为共享内存的存储区(SM3.0的设备共享内存大小为64KB)进行访问,并且在执行的任一时刻都可以进行同步. GPU上还有一块叫做全局内存的存储区,其容量较大,GTX680上的全局内存达到2GB. GPU上所有的线程均可访问全局内存,但全局内存的访问速度却比共享内存慢两个数量级.因此,英伟达公司提供了一种叫存储合并的技术为特定连续数据的存储访问提供优化方案.由于GPU的计算与存储都是并行执行的,因此,许多算法的主要瓶颈都出现在CPU与GPU全局内存的数据传输上以及全局内存的访问,另外合理利用共享内存也能对程序的加速做出很大贡献.
为了充分挖掘GPU的性能,有两点必须注意.首先,CPU与GPU全局内存的数据传输次数应尽量少.对于机器学习和模式识别问题,可以通过将原型模型数据一直保存在GPU全局内存的方式来减少数据的传输次数.然而,有时全局内存并不能保存所有的训练数据,此时可以只在使用时传输相应的数据,每次传输的数据量尽量多,以此保证总体的传输次数最少.由于原型参数数据以及训练数据均保存在GPU的全局内存中,参数的更新操作也可以直接在GPU上完成.
另外需要注意的一点是学习算法的设计和实现需考虑线程块与线程这两个层面,这样才能高效使用共享内存,实现全局内存合并访问.通常,线程块的选取控制着整体数据并行策略,而线程块内的线程通过使用共享内存和同步操作,控制着最底层的并行效果.此外,已调度到SM上准备执行的线程块在等待全局内存访问时,图形硬件能很好地隐藏存储延迟.为了充分利用这些延迟时间,线程块的数量可以尽量多,且相互之间独立执行.
根据以上两点并行设计原则,本文提出一种可以把密集型计算分发到GPU上的计算框架,其流程图如图 1所示.图中GPU与CPU控制权的更迭用虚线箭头表示.由图 1可知:原型向量只在程序启动时传输到GPU上,并在程序结束时从GPU传输回CPU;若全局内存无法一次性容纳整个训练集,则通过小批量处理的方式分批将训练样本传输到GPU全局内存(CPU和GPU端的数据传输采用曲线箭头表示),否则,只需一次性将所有数据拷贝到GPU.整个执行过程中,仅在流程控制和准备数据上,需要少量的CPU干预.

|
图 1 原型学习的异构计算模型 Figure 1 Heterogeneous computing model for prototype learning |
本文的算法实现采用CUDA并行编程架构.在每轮的训练过程中主要调用了3个CUDA核函数.算法2中的第3到6步分别在3个独立的核函数中执行,其中第4步和第5步在同一核函数内执行.在这3个核函数中,前2个最消耗时间,是所谓的“热点”.针对这2个核函数,本文分别提供了两种不同的并行计算算法,并对其效率进行分析.
2.1 基于并行归约的距离计算归约操作可以在K个输入元素上执行操作,转化得到1个输出元素.它可以用来并行执行可交换的二元操作.标准的归约算法可以在文献[12]中找到.此处采用归约算法来计算两个向量之间的欧氏平方距离.在计算过程中,需定义操作符⊕:
| $ {a_i} \oplus {b_i} \equiv + {\left( {{a_i}-{b_i}} \right)^2}. $ |
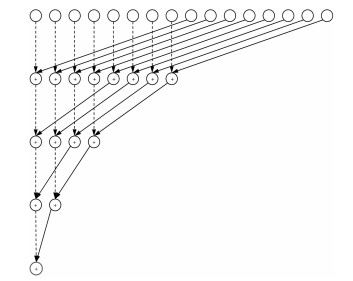
图 2显示了16个线程时的归约结构(每个线程处理一个元素).第一轮计算时,前8个元素依序与后8个元素进行操作符为⊕的运算.第二轮则是前8个元素中的前4个元素与后4个元素对应运算.以此类推.假设K是2的幂次倍,对于一个K维的向量则只需要计算log2(K)+1轮就能得到平方距离.
|
图 2 归约过程示意(以16元素为例) Figure 2 Reduction of 16 elements |
初始时,每个线程块从全局内存加载一个样本向量和原型向量,负责一个平方距离的计算.因此,一共需要(C, mb)个线程计算C×mb个平方距离.
然而,在具体实现的时候,仍有许多细节问题需要注意.例如有时样本特征向量的维度(用dim表示)并不是2的幂次倍,如160.此时,线程块的线程数目仍可以开启为2的幂次倍,但其大小必须是小于特征向量的维度和物理硬件允许的线程块线程数目的最大2的幂次值.对于超出线程块大小的数据,可以在进行对数步(log-step)归约之前,通过额外一次⊕运算累加到线程块前部线程的部分和上.另外,程序应尽可能复用共享内存.相较于一个线程块计算一个平方距离,也可以让每个线程块计算一个样本与TILE_LEN个原型之间的欧氏距离,以提高样本数据的利用率.
2.2 基于分块加和的距离计算与归约算法不同,该算法的思想是一个线程独立计算一个欧氏距离,每个线程首先从全局内存中获取2个维度为dim的向量,然后执行一个序列化的归约操作.但这样读取全局内存的效率并不高,容易造成阻塞.为了解决矩阵乘法任务中全局内存的访问阻塞问题,文献[13]采用基于数据分块思想进行改善.这种思想进行适当改进,也能很好地用来解决这里的平方距离的计算问题.
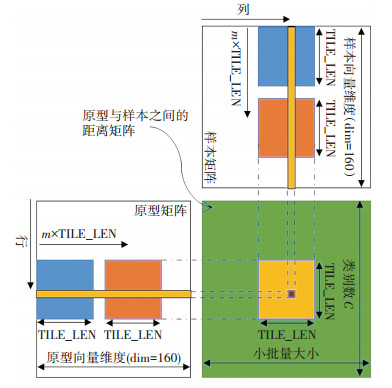
算法的整体目标是计算mb×C个距离,因此可以将这些距离看做一个矩阵,并将这个矩阵划分为TILE_LEN×TILE_LEN个块,每个分块的维度大小与线程块的大小相同. TILE_LEN值的选择受到可用共享内存大小的限制和线程块大小的限制,必须保证每个线程块的共享内存能够容纳该线程块内的所有计算数据.然后把样本矩阵与原型矩阵也照此划分成块.因此,每个线程计算平方距离需要(dim+TILE_LEN-1)/TILE_LEN个阶段,每个向量距离均是通过迭代累加而得.该算法的详细过程如图 3所示.利用这种方法,全局内存的访问次数可减少到原来的1/TILE_LEN.
|
图 3 通过分块思想实现平方距离的计算 Figure 3 Caculation of squared distances via tiling idea |
当计算出样本(xn, yn)与C个原型的距离后,接下来的任务就是找出该类的真实类别(含额外的距离信息)(dc, c)与竞争类别(含额外的距离信息) (dr, r).从而可以通过梯度下降方法更新mc与mr.这里提出一种并行归约的方式来寻找与该样本最近的距离以及与其对应的原型索引,并通过一些技巧来避免程序的条件判断代码.例如,既然dr是除了dc之外的最小距离,在程序执行时,可先通过yn获取到dc,然后将其设为一个无限大的值,以防止寻找最小距离时需要对dc进行特别的判断操作.若每个类使用多个原型中心,则需要提前通过一遍归约操作来计算出最近的原型索引.
算法的内核函数启动了mb个线程块,每个线程块包含1024(或512)个线程.同一个线程块内的所有线程将在共享内存中做归约操作,找出与该样本距离最近的竞争类别.同样,若类别数C不为2的幂次倍,也可采用3.1节中相同的技巧.另外,C可能比一个线程块包含的线程数还要大,此时需要在进行对数步归约之前先对那些相距线程块大小的数据进行迭代加和.
2.4 基于比较交换的最小距离搜索该算法只需调用mb个线程,每个线程通过比较交换操作找出一个样本的真实类别(含额外的距离信息)(dc, c)与竞争类别(含额外的距离信息) (dr, r).若mb比线程块理论最大线程数还大,则需要分配多个线程块.
该算法是对串行搜索算法进行的最粗粒度的并行化.一个线程将要执行时间复杂度为O(C)的操作才能得到输出,因此这是一种线程密集型的处理策略.若mb的值很小,则无法充分利用GPU的资源.
2.5 参数更新若使用随机梯度下降(即mb=1),则每次更新时只需对两个原型向量进行更新,即真实类别原型向量和竞争类别原型向量.参数更新的内核函数只需调用dim个线程,每个线程按式(2)对向量的一个元素进行更新.当mb>1时,每个线程需要迭代mb次,每轮迭代都考虑来自一个样本的贡献,对两个原型向量进行更新.
3 验证将本文中的异构原型学习算法在大规模、大类别手写汉字识别任务上进行测试,验证过程中主要对每类单个原型和每类8个原型的情况进行测试,TILE_LEN的大小设置为16.算法测试的硬件平台采用统一的GPU服务器.计算机配置有Xeon X3440服务器级CPU,主频为2.53 GHZ.消费级显卡GTX680插在服务器的PCI-E插槽上.当考虑算法在未来硬件上的适应性时,使用了更新的显卡GTX980.
3.1 汉字样本库描述本文使用的汉字数据库为CASIA-HWDB1.0 (DB1.0)与CASIA-HWDB1.1 (DB1.1)[15],这是文献[2]中使用的数据库的子集,其包含3 755个类别(来自国标GB1字符集),每个类约有570个训练样本.这样共有2 144 749个训练样本,533 675个测试样本.在收集样本时,每一套字符集按照6种不同的排列次序预先打印在版面上,为的是抵消每个书写者在书写过程中的书写质量变化.
为了描述每个样本,提取512维的梯度特征作为特征向量.随后使用线性判别分析(LDA)将特征向量从512维降到160维.因此,本文中使用的变量dim大小为160.
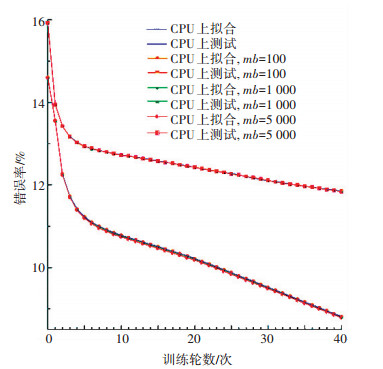
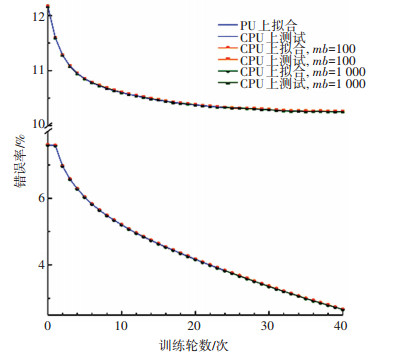
3.2 算法正确性验证同时运行CPU版本的GLVQ算法与异构计算架构版本的GLVQ算法进行背对背测试,且均在训练数据上运行40轮.每轮测试都计算出训练样本上的识别错误率以及测试样本的识别错误率.实验中也对不同大小的mb进行了测试,图 4与图 5分别显示了整个学习过程以及对应的性能.鉴于基于CPU的串行算法的训练过程过于耗时,图 5中仅训练了24轮.由图可知,串行版本的GLVQ算法与异构计算架构版本的GLVQ算法的运行结果并无明显差异,这说明本文提出的适用于异构计算架构的大规模GLVQ算法具备正确性.
|
图 4 比较CPU版本和GPU异构版本的学习过程(每类单个原型) Figure 4 Learning process comparison between CPU and GPU (single prototype/class) |
|
图 5 比较CPU和GPU的学习过程(每类八个原型) Figure 5 Learning process comparison between CPU and GPU (eight prototypes/class) |
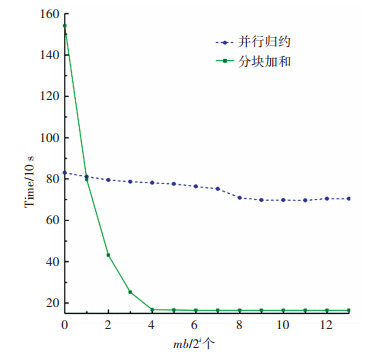
算法1中距离计算与最短距离搜索这两步的计算量最大.首先对距离计算的效率进行评估.实验中主要使用了归约和分块加和两种算法,并比较了不同mb大小时的运算效率. mb的大小分别取{20, 21, …, 213}.实验结果如图 6与图 7所示,实验只对训练数据进行了一轮测试.由图可知,并行归约算法的执行时间比较稳定,在小批量的规模较小时,应优先使用并行归约算法.而当mb的值大于或等于TILE_LEN时,分块加和算法则效率更高

|
图 6 分别基于并行归约和分块加和计算距离的比较(每类单个原型) Figure 6 Distance computation comparison between parallel reduction and tiling sum (single prototype/class) |
|
图 7 分别基于并行归约和分块加和计算距离的比较(每类八个原型) Figure 7 Distance computation comparison between parallel reduction and tiling sum (eight prototypes/class) |
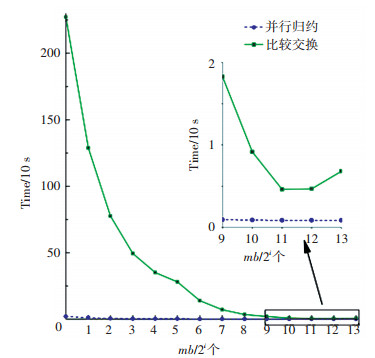
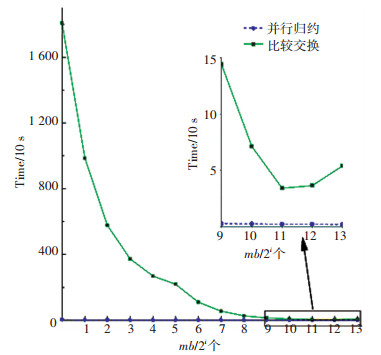
对于最短距离搜索的实现,采用了并行归约和比较交换两种方案.对这两种方案进行一轮学习测试,测试结果如图 8与图 9所示.从图中可以看出,并行归约算法的可扩展性更强,针对不同的mb值算法的执行时间都比较稳定,即使当mb很大时,比较交换算法仍比并行归约慢很多.另外,当一个类使用多个原型向量时,比较交换算法的效率就变得更差.图中同样显示,当使用过大的mb时,会带来少量的额外消耗.很重要的原因在于mb取值很大时,可能损害GPU系统缓存的效率.
|
图 8 分别基于并行归约和比较交换策略求最小值的比较(每类单个原型) Figure 8 Minima searching comparison between parallel reduction and compare-and-exchange (single prototype /class) |
|
图 9 分别基于并行归约和比较交换策略求最小值的比较(每类八个原型) Figure 9 Minima searching comparison between parallel reduction and compare-and-exchange (eight prototypes/class) |
训练GLVQ模型的串行学习过程比较耗时。若使用单核CPU进行一轮学习,当每个类使用单个原型时需要花费4 332 s,而每类使用8个原型则需要消耗32 843 s.若对GLVQ算法循环训练40轮,则需要花费数天时间.
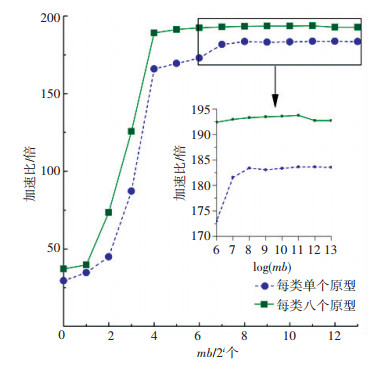
基于本文提出的异构并行学习框架,开发了一个可根据计算负载规模自适应切换最优内核函数的GLVQ原型学习算法.分别针对每类单个原型和每类8个原型的情况,收集数据并计算算法的加速比,如图 10所示.加速比的计算是采用串行执行时间除以并行执行时间.可从图 10看出,当使用本文所提出的异构原型学习算法时,每类使用单个原型时运行速度最高可加速184倍,而每类使用8原型则最高可加速194倍.
|
图 10 异构大规模原型学习相对CPU的加速比(分别考虑每类单个原型和每类八个原型) Figure 10 Prototype learning speedup (with both single prototype/class and eight prototypes/class) |
这里需要强调,并不是小批量规模越大,加速越高.加速峰值均出现在小批量mb=2 048个样本时,说明此时GPU的计算部件的利用率和访存效率之间经折衷后达到最优.一旦继续加大小批量的规模,虽然可以加大GPU的占用率,但会对参加运算数据的局部性有所损害,从而导致GPU硬件二级缓存的命中率降低.以每类单个原型为例,从mb=2 048增加小批量的规模到mb=8 196,GPU的占用率从98.08%增加为98.13%,但却导致二级缓存的命中率从91.0%恶化到87.1%.缓存命中率的下降,意味着访存效率的恶化,由于占用率的增加无法抵消访存恶化的负面效应,最终影响了每秒可以执行的浮点以及整型运算数量.在本文的实验中,随着mb的进一步增大,加速比的下降幅度一般较小.
随机梯度下降模式(mb=20)通常很难达到较高的加速比,这是由于受到可并行化的计算负载的局限.当采用随机梯度下降时,本文中距离计算与最短距离搜索均采用并行归约的算法,以此实现细粒度并行.最终,本文的方法在随机梯度下降模式下实现了最少30倍的加速比(每类单个原型时30倍,每类8个原型时37倍),这一成绩在文献上比较少见.
最后,讨论所提出框架在未来新GPU硬件上的扩展性和适应性.当前,在消费级显卡行业出现了计算能力高于GTX680的GPU硬件,GTX980是典型代表.本文的原型学习算法未做任何修改,重新运行在GTX980上并考察在新硬件上的性能表现.当采用随机梯度下降模式时,两种原型分配方案下获得的加速比分别为30倍(每类单个原型)和38倍(每类8个原型),跟GTX680的加速比例相当.但当采用小批量处理模式时,可以看到更优异的性能提升:每类分配单个原型时获得加速比为493倍,每类8个原型时的加速比为638倍.这表明本文的异构并行学习框架对于未来的新硬件具有较强的自动扩展能力.
4 结语本文提出的适用于异构计算架构的大规模原型学习算法框架通过重组串行原型学习算法的计算任务,将串行学习算法转化为高度并行化的形式,可以将密集型计算负载转移到GPU上,而CPU只需进行少量的流程协调和数据传递.为了充分利用GPU的资源,该算法框架可自动选择分块策略与并行归约策略.算法的正确性和有效性均在大规模手写汉字识别任务上进行了验证.在消费级显卡GTX680上使用小批量处理模式进行模型学习时,最高可得到194倍的加速比,即使是随机梯度下降模式下,也可实现30倍的加速比.当升级显卡到GTX980,在小批量下的加速比可提升到638倍,表明本文提出的框架和算法具有很好的可扩展性和适应性,能够有效解决原有原型学习的计算瓶颈问题.
| [1] | LIU C, NAKAGAWA M. Evaluation of prototype learning algorithms for nearest-neighbor classifier in application to handwritten character recognition[J]. Pattern Recognition,2001, 34 : 601-615. DOI: 10.1016/S0031-3203(00)00018-2 |
| [2] | SU T, LIU C, ZHANG X. Perceptron learning of modified quadratic discriminant function[C]//International Conference on Document Analysis and Recognition. 2011:1007-1011. http://www.nlpr.ia.ac.cn/2011papers/gjhy/gh46.pdf |
| [3] | LV Y, HUANG L, et al. Learning-based candidate segmentation scoring for real-time recognition of online overlaid Chinese handwriting[C]//International Conference on Document Analysis and Recognition. 2013: 74-78. https://www.researchgate.net/publication/261499607_Learning-Based_Candidate_Segmentation_Scoring_for_Real-Time_Recognition_of_Online_Overlaid_Chinese_Handwriting |
| [4] |
苏统华, 戴洪良, 张健, 等. 面向连续叠写的高精简中文手写识别方法研究[J].
计算机科学,2015, 42 (7) : 300-304.
SU T, DAI H, et al. Study on High Compact Recognition Method for Continuously Overlaid Chinese Handwriting[J]. Computer Science,2015, 42 (7) : 300-304. |
| [5] | SU T, MA P, et al. Exploring MPE/MWE training for Chinese handwriting recognition[C]//International Conference on Document Analysis and Recognition. 2013:1275-1279. |
| [6] | ZHOU M, YIN F, LIU C. GPU-based fast training of discriminative learning quadratic discriminant function for handwritten Chinese character recognition[C]//International Conference on Document Analysis and Recognition, 2013:842-846. https://www.researchgate.net/publication/261499993_GPU-Based_Fast_Training_of_Discriminative_Learning_Quadratic_Discriminant_Function_for_Handwritten_Chinese_Character_Recognition |
| [7] | GELSINGER P. Microprocessors for the new millennium: Challenges, opportunities and new frontiers[C]//ISSCC Tech. Digest, 2001: 22-25. |
| [8] | RAINA R, MADHAVAN A, NG A Y. Large-scale deep unsupervised learning using graphics processors[C]//International Conference on Machine Learning. 2009. 873-880. |
| [9] | SCHERER D, SCHULZ H, BEHNKE S, Accelerating large-scale convolutional neural networks with parallel graphics multiprocessors[C]//International conference on Artificial neural networks. 2010:82-91. https://www.researchgate.net/profile/Sven_Behnke/publication/221080133_Accelerating_Large-Scale_Convolutional_Neural_Networks_with_Parallel_Graphics_Multiprocessors/links/0fcfd5012d53f701bb000000.pdf |
| [10] | CIRESAN DC, MEIER U, et al. Deep, big, simple neural nets for handwritten digit recognition[J]. Neural computation,2010, 22 : 3207-3220. DOI: 10.1162/NECO_a_00052 |
| [11] | JIN X, LIU C, HOU X. Regularized margin-based conditional log-likelihood loss for prototype learning[J]. Pattern Recognition,2010, 43 (7) : 2428-2438. DOI: 10.1016/j.patcog.2010.01.013 |
| [12] | SATO A, YAMADA K. Generalized learning vector quantization[C]//Advances in Neural Information Processing Systems. 1996: 423-429. |
| [13] |
WILT N. CUDA专家手册: GPU编程权威指南[M].苏统华等, 译.北京:机械工业出版社, 2014.
WILT N. The CUDA Handbook: A Comprehensive Guide to GPU Programming[M]. Addison-Wesley, 2013. |
| [14] |
KIRK DB, WENMEI WH.大规模并行处理器编程实战[M].赵开勇等, 译.第二版.北京:清华大学出版社, 2013.
KIRK DB, WENMEI WH. Programming massively parallel processors: a hands-on approach (Second Edition)[M]. Morgan Kaufmann, 2012. |
| [15] | LIU C, YIN F, et al. Online and offline handwritten Chinese character recognition: Benchmarking on new databases[J]. Pattern Recognition,2013, 46 (1) : 155-162. DOI: 10.1016/j.patcog.2012.06.021 |
 2016, Vol. 48
2016, Vol. 48


