2. 北京航空航天大学 电子信息工程学院, 北京 100191
2. College of Electronic and Information Engineering, Beihang University, Beijing 100191, China
L频段数字航空通信系统1(L-DACS1)是民航未来沿陆地航路部署的空-地蜂窝移动通信系统,主要为陆地航路、终端区及机场的航空器提供空中交通管制、航空公司运营管理数据通信服务,是民航未来航空移动通信系统的主要技术手段之一[1].依据国际民航组织的规划,L-DACS1系统将以内嵌的方式部署在L频段测距仪(DME)的波道间,占用传输带宽500KHz[2-3].由于DME与OFDM信号频谱存在部分交叠,且DME系统发射功率较高,不可避免产生DME信号干扰L-DACS1系统OFDM接收机的问题[4-5],因此开展OFDM接收机DME干扰抑制的研究具有重要意义.
目前,L-DACS1系统DME干扰抑制的研究主要集中在单天线干扰消除及阵列天线干扰抑制两个方面.在单天线干扰消除方面,文献[6-7]利用DME干扰信号在时域呈现脉冲干扰的特点,提出脉冲熄灭干扰抑制法,该方法主要缺点:在时变信道环境下,脉冲熄灭门限的精确设置非常困难.为解决脉冲熄灭导致OFDM信号产生子载波间干扰(ICI)的问题,文献[8-10]提出脉冲熄灭ICI干扰补偿方法,该方法主要缺点:ICI干扰补偿法要求精确知晓各个子信道的衰落信息,而在干扰环境下OFDM接收机各个子信道衰落信息的精确获得本身就非常困难.在阵列天线在航空移动通信应用方面,文献[11]提出在无人机平台中搭载移动基站为偏远地区提供移动通信服务的构想,文献[12-14]构建了机载实验系统验证了在无人机平台使用阵列天线进行大容量空-地数据通信的可行性.另外,在基于阵列天线的L-DACS1系统OFDM接收机DME干扰抑制方面,文献[15]提出利用正交投影算法消除高强度DME干扰,然后采用盲波束形成方法提取OFDM直射径信号的方法,该方法存在不足:当测距仪干扰较小时,正交投影干扰抑制性能较差.在正交投影消除脉冲干扰方法基础上, 文献[16]进一步提出利用CLEAN算法估计OFDM直射径信号来向的方法,并通过常规波束形成算法提取OFDM直射径信号,该方法主要不足:当接收OFDM信号功率较低且数据快拍较少时,提出方法的DOA估计性能较差.
针对高强度测距仪信号干扰L-DACS1系统OFDM接收机的问题,本文提出联合DOA估计与主波束形成的干扰抑制方法.首先接收机利用DME与OFDM信号空域来向的差异,通过波达方向矩阵法获取各来向信号的DOA;然后利用各个来向信号的DOA信息通过线性约束最小方差(LCMV)波束形成算法确定各来向信号波束形成的权值,并利用波束形成权值对接收信号进行波束形成以分离出各个来向信号;最后利用OFDM与DME信号时频特征的差异,通过频域功率与时域功率比较算法获得OFDM直射径信号.仿真结果显示:提出的方法可有效抑制DME及OFDM散射径信号干扰,提高链路传输的可靠性.
1 系统模型 1.1 联合DOA估计与主波束形成的OFDM接收机图 1为联合DOA估计与主波束形成的OFDM接收机原理框图.接收机均匀圆阵输出信号通过A/D转换为数字基带信号,数字基带信号通过波达方向估计器估计各个来向信号的DOA信息.随后阵列接收信号及DOA信息同时送入主波束形成器,主波束形成器通过线性约束最小方差算法(LCMV)计算各来向信号的波束形成权值,然后通过波束形成提取各个来向信号.提取的各个来向信号同时送入信号分类器,在信号分类器中通过频域功率与时域功率比较算法分辨DME及OFDM信号,并输出OFDM直射径信号.信号分类器输出的OFDM直射径信号经多普勒频偏估计与补偿后移除循环前缀(CP),送入FFT转换器变换为频域信号.频域信号经频域下采样后送入信道估计及均衡器完成信道均衡,均衡器输出信号经解调器、解交织器后送入信道译码器恢复出原始发送比特序列估值.
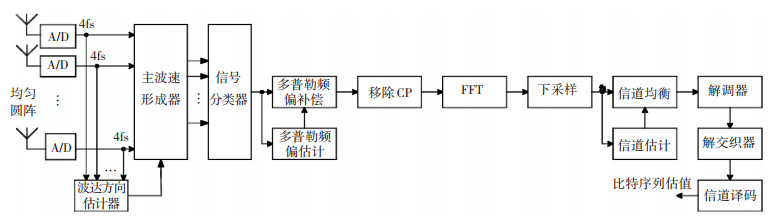
|
图 1 联合DOA估计与主波束形成的OFDM接收机原理 Figure 1 OFDM receiver based on joint DOA estimation and main beam forming |
为解决相干信号环境下均匀圆阵二维DOA估计问题,采用文献[17]提出的波达方向矩阵法解决相干信源的二维DOA估计问题.接收机使用上下平行双均匀圆阵(如图 2所示),上下间隔d=λ/2,上下子阵的阵元位置一一对应,每个子阵的阵元数均为M,圆半径均为R,信号波长为λ.
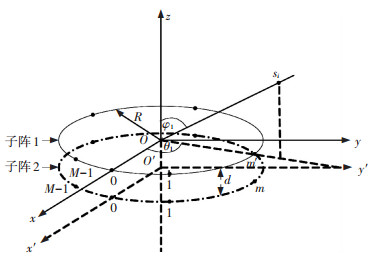
|
图 2 双均匀圆阵结构图 Figure 2 Structure of double uniform circular array |
考虑以子阵1的圆心为参考点,则子阵1中第m个阵元坐标为(xm, ym, 0),第m个阵元的输出信号为
| $ \begin{array}{c} {x_m}\left( t \right) = \sum\limits_{i = 1}^I {{s_i}\left( t \right){{\rm{e}}^{-{\rm{j}}\frac{{2R\pi }}{\lambda }\sin \left( {{\varphi _i}} \right)\cos \left( {{\theta _i}-\frac{{2m\pi }}{M}} \right)}} + {n_{1m}}\left( t \right)} \\ m = 0, 1, \cdots, M-1. \end{array} $ |
式中: si(t)代表阵列天线接收的第i个信号源,{θi, φi}代表第i个信号源的方位角和俯仰角,n1m(t)代表信道输入的窄带高斯白噪声,I代表阵列接收信号源总数.类似的,子阵2上坐标为(xm, ym, -d)的阵元输出信号为
| $ \begin{array}{l} {y_m}\left( t \right) = \sum\limits_{i = 1}^I {{s_i}\left( t \right){{\rm{e}}^{-{\rm{j}}\frac{{2R\pi }}{\lambda }\sin \left( {{\varphi _i}} \right)\cos \left( {{\theta _i}-\frac{{2m\pi }}{M}} \right) + {\rm{j}}\frac{{2\pi }}{\lambda }d\cos \left( {{\varphi _i}} \right)}} + {n_{2m}}\left( t \right)} \\ \;\;\;\;\;\;\;\;\;\;m = 0, 1, \cdots, M-1. \end{array} $ |
利用文献[17]的DOA方法计算信号俯仰角和方向角得
| $ \begin{array}{c} {{\hat \varphi }_i} = \arccos \left[{\frac{\lambda }{{2{\rm{\pi }}R}} \cdot {\rm{Arg}}\left( {{\eta _i}} \right)} \right], i = 1, 2, \cdots, I\\ {{\hat \theta }_i} = \frac{1}{M}\sum\limits_{j = 0}^{M - 1} {\left[{\frac{{{\rm{j}}2{\rm{\pi }}}}{M} + \arccos \left( {\frac{\lambda }{{2{\rm{\pi }}R}} \cdot \frac{1}{{\sqrt {1-{{\left( {\frac{\lambda }{{2{\rm{\pi }}d}} \cdot {\rm{Arg}}\left( {{\eta _i}} \right)} \right)}^2}} }}{\rm{Arg}}\left( {{\varepsilon _i}\left( j \right)} \right)} \right)} \right]}, i = 1, 2, \cdots, I. \end{array} $ |
式中:R代表按照文献[17]中方法构造的空域平滑波达方向矩阵,ηi和εi分别代表R的特征值和对应特征矢量,εi(j)代表εi中的第j个元素,Arg(·)代表幅角主值运算.
1.3 主波束形成算法图 3给出了主波束形成器框图.主波束形成器由I个并行的线性约束最小方差(LCMV)波束形成器组成.假设阵列接收信号为V(n),则第i个线性约束最小方差波束形成器输出信号为
| $ {x_i}\left( n \right) = \boldsymbol{w}_i^H \cdot \boldsymbol{V}\left( n \right), i = 1, 2, \cdots, I. $ |
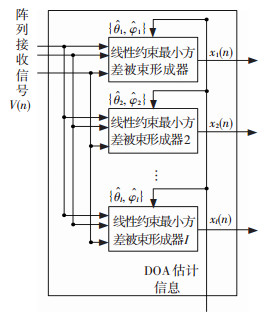
|
图 3 主波束形成器 Figure 3 Main beamforming |
其中,I代表阵列天线接收OFDM信号及测距仪信号源总数,wi代表第i个来向信号波束形成权值[19]:
| $ {w_i} = \boldsymbol{R}_v^{-1}{\boldsymbol{C}_i}{\left( {\boldsymbol{C}_i^H\boldsymbol{R}_v^{-1}{\boldsymbol{C}_i}} \right)^{-1}}\boldsymbol{f}, i = 1, 2, \cdots, I. $ |
式中:Rv代表接收信号协方差矩阵;f=[1 0 … 0]T;Ci代表约束矩阵,满足
| $ {\boldsymbol{C}_i} = [{\boldsymbol{a}_i}\left( {{{\hat \theta }_i}, {{\hat \varphi }_i}} \right){\boldsymbol{C}_{I-1}}] $ |
式中:
图 4给出接收机信号分类器的原理框图.信号分类器由频域功率比较器和时域功率比较器两个单元组成.其中,频域功率比较器用于分辨DME与OFDM信号,时域功率比较器用于分辨OFDM直射径与散射径信号.
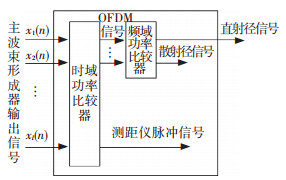
|
图 4 信号分类器 Figure 4 Signal classification |
根据OFDM及DME信号的频域特征[4],OFDM信号的能量主要集中于[-250 kHz~+250 kHz],测距仪信号的能量主要位于±250 kHz处, 因此可通过比较接收信号在频域±250 kHz及直流子信道附近平均功率的方法来分辨接收信号的类型.
假设接收机已建立定时同步,主波束形成器输出信号xi(n)在移除循环前缀后通过FFT转换为频域信号Xi(k).定义参量Pi, 0:
| $ {{\bar P}_{i, 0}} = \frac{1}{J}\sum\limits_{k =-J/2, k \ne 0}^{J/2} {{{\left| {{X_i}\left( {{n_0} + k} \right)} \right|}^2}, i = 1, 2, \cdots, I.} $ | (1) |
式中:n0代表直流子信道的位置索引,Pi, 0代表第i路信号xi(n)在直流子信道附近J个子信道的平均功率(J取正偶数).同理,定义参量Pi, 250:
| $ {{\bar P}_{i, 250}} = \frac{1}{J}\sum\limits_{k = 0}^{J-1} {{{\left| {{X_i}\left( {{n_1} + k} \right)} \right|}^2}, i = 1, 2, \cdots, I.} $ | (2) |
式中:n1代表 250 kHz处子信道的位置索引,Pi, 250代表 250 kHz处子信道右侧J个子信道的平均功率.同理,定义参量Pi, -250:
| $ {{\bar P}_{i, -250}} = \frac{1}{J}\sum\limits_{k = 0}^{J-1} {{{\left| {{X_i}\left( {{n_2}-k} \right)} \right|}^2}, i = 1, 2, \cdots, I.} $ | (3) |
式中:n2代表-250 kHz处子信道的位置索引,Pi, -250代表-250 kHz处子信道左侧J个子信道的平均功率.
以式(1)~(3)定义的参量为基础,给出频域功率比较器判定准则:如果Pi, 0>Pi, 250同时Pi, 0>Pi, -250,则待检测信号xi(n)被判定为OFDM信号;如果Pi, 250>Pi, 0或Pi, -250>Pi, 0,则待检测信号xi(n)被判定为DME信号.
1.4.2 时域功率比较器如果待检测信号被判定为OFDM信号,则还需要进一步判定待检测信号是OFDM直射径还是散射径信号.由于航空移动信道呈现为赖斯信道[18],信道的赖斯因子取值为15~20 dB,因此OFDM直射径信号功率远高于散射径,可直接通过比较各个OFDM信号的功率来分辨OFDM直射径.
2 数值仿真及分析 2.1 仿真环境设置为验证联合DOA估计与主波束形成干扰抑制方法的正确性,按照L-DACS1系统技术规范[3]设计实现L-DACS1系统阵列天线干扰抑制仿真系统,仿真参数如表 1所示.
| 表 1 L-DACS1系统仿真环境 Table 1 Simulation environment of L-DACS1 system |
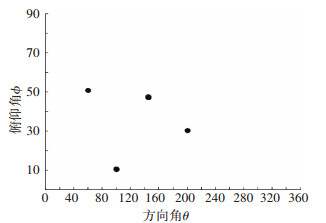
图 5给出不同信源的DOA估计性能,横坐标代表方位角(度),纵坐标代表俯仰角(度).仿真实验中,OFDM直射径来向(60°, 50°),散射径来向(140°, 40°),信噪比SNR=10 dB;DME信号1来向(100°, 10°),信干比SIR=-3 dB,载波偏置+500 KHz;DME信号2来向(200°, 30°),信干比SIR=-10 dB,载波偏置-500 KHz.由图 5可观测到:1) OFDM直射径与DME信号来向的估计值与预设值完全一致;2) OFDM散射径来向的估计值与预设值存在微小的偏差.
|
图 5 DOA估计性能(SNR=10 dB,SIR=-3/-10 dB,赖斯因子=10 dB,200次仿真实验) Figure 5 DOA estimation (SNR=10 db, SIR=-3/10 dB, rice factor=10 dB, simulations for 200 times) |
图 6给出不同信源DOA估计的根均方误差曲线,横坐标代表信噪比(dB),纵坐标代表根均方误差值(度).根均方误差值定义为
| $ {\rm{RMSE = }}\sqrt {\frac{1}{N}\sum\limits_{i- 1}^N {\left[{{{\left( {{{\hat \theta }_{ij}}-{{\hat \theta }_i}} \right)}^2} + {{\left( {{{\hat \varphi }_{ij}}-{{\hat \varphi }_i}} \right)}^2}} \right]} }, $ |
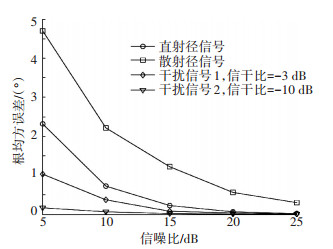
|
图 6 DOA估计根均方误差曲线(赖斯因子=10 dB) Figure 6 Root mean square error curve of DOA estimation(Rice factor=10 dB) |
(θi, φi)代表第i个信源到达角的预设值,
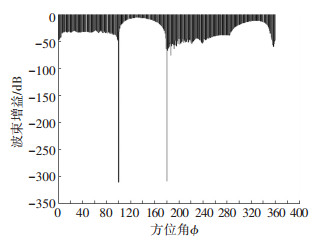
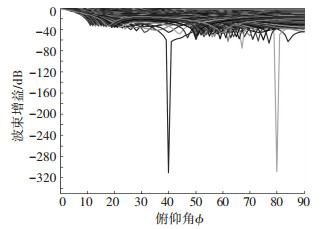
图 7和图 8分别给出LCMV算法波束图,图 7横坐标代表方位角,图 8横坐标代表俯仰角,两图纵坐标均代表归一化波束增益(dB).由图 7与图 8可观测到:阵列天线的波束在干扰信号1来向(100°, 10°)、干扰信号2来向(200°, 30°)及OFDM散射径来向(140°, 40°)形成零陷,零陷衰减达-300 dB,表明了提出方法可有效抑制DME及OFDM散射径信号的干扰.
|
图 7 LCMV算法在方位角上的波束图(SNR=10 dB, SIR=-3 dB/-10 dB, 200次蒙特卡罗实验) Figure 7 LCMV beamforming on azimuth angle(SNR=10 dB, SIR=-3 dB/-10 dB for Montacarlo test for 200 times) |
|
图 8 LCMV算法在俯仰角上的波束图(SNR=10 dB, SIR=-3 dB/-10 dB, 200次蒙特卡罗实验) Figure 8 LCMV beamforming on pitch angle(SNR=10 dB, SIR=-3 dB/-10 dB.Montacarlo test for 200 times) |
图 9给出波束形成性能随DOA估计误差变化曲线,横坐标代表DOA估计误差(方向角误差+俯仰角误差),纵坐标代表波束形成输出信号(OFDM直射径信号)信噪比.由图 9观测到:1)输出信噪比随DOA估计误差的增大可逐渐降低;2)理想DOA时,波束形成输出信噪比为1 dB,对输入信噪比提升约5 dB.

|
图 9 DOA估计偏差对波束形成性能影响曲线(输入信噪比为-4 dB) Figure 9 Beamforming performance based on the DOA estimation deviation (input SNR=-4 dB) |
图 10给出信号分类器判定差错概率的性能曲线,横坐标代表信噪比,纵坐标代表信号分类器判定OFDM直射径、OFDM散射径及DME信号出现错误的概率.由图 10观测到:判定差错概率随输入信噪比的增加而快速降低,当输入信噪比为6 dB时,判定出现差错的概率为1.0×10-4.考虑到典型情况下OFDM接收机输入信噪比高于6 dB,因此提出的信号分类器能够准确分辨OFDM直射径、OFDM散射径及DME信号.

|
图 10 信号分类器差错概率性能(OFDM直射径信号、散射径信号、单个DME信号、信干比=-10 dB) Figure 10 Error probability performance of signal classification |
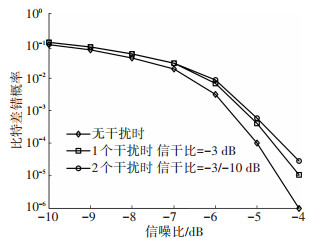
图 11给出OFDM接收机比特差错性能曲线,横坐标代表信噪比(dB),纵坐标代表比特差错概率. 图 11共包含4曲线:标有“◆”的曲线代表无干扰信号时系统比特差错性能;标有“■”的曲线代表存在一个干扰信号时系统比特差错性能;“●”的曲线代表存在两个干扰信号时系统比特差错性能;标有“▼”的曲线代表按照文献[15]方法仿真得到的比特差错性能.曲线比较表明:所提方法可完全克服DME干扰信号对OFDM接收机链路传输的影响,且性能优于文献[15]提出的方法.
|
图 11 L-DACS1系统比特差错性能 Figure 11 Bit error performance of L-DACS1 system |
针对高强度测距仪脉冲信号干扰L-DACS1系统OFDM接收机问题,提出联合DOA估计与主波束形成的干扰抑制方法.该方法首先利用DME与OFDM信号空域来向的差异,通过线性约束最小方差波束形成算法分离各个信号,随后借助OFDM与DME信号的时频特征的差异,分辨并输出OFDM直射径信号.仿真研究表明:提出的方法可有效克服DME信号及OFDM散射径的干扰,提高接收机链路传输的可靠性.
| [1] | SCHELL M, EPPLE U, SHUTIN D, et al. L-DACS: future aeronautical communications for air-traffic management[J]. IEEE Communications Magazine,2014, 25 (5) : 104-110. |
| [2] | NEJI N, LACERDA DE R, AZOULAY A, et al. Survey on the future aeronautical communication system and its development for continental communications[J]. IEEE Transactions Vehicular Technology,2013, 62 (1) : 182-191. DOI: 10.1109/TVT.2012.2207138 |
| [3] | SAJATOVIC M, HAINDL B, EHAMMER M, et al. L-DACS1 system definition proposal: deliverable D2[S]. Version 1.0. Brussels: Eurocontrol, 2009:1-173. |
| [4] | EPPLE U, SCHELL M. Overview of legacy systems in L-band and its influence on the future aeronautical communication system LDACS1[J]. IEEE Aerospace and Electronic Systems Magazine,2014, 29 (2) : 31-37. DOI: 10.1109/MAES.2014.120092 |
| [5] | EPPLE U, SCHELL M. Overview of interference situation and mitigation techniques for LDACS1[C]//2011 IEEE/AIAA 30th.Digital Avionics Systems Conference (DASC).Seattle, WA: IEEE, 2011: 4C5-1-4C5-12. |
| [6] | EPPLE U, HOFFMANN F, SCHELL M. Modeling DME interference impact on LDACS1[C]//IEEE.Integrated Communications, Navigation and Surveillance Conference (ICNS). Herndon, VA:IEEE, 2012: G7-1-G7-13. |
| [7] | EPPLE U, BRANDES S, GLIGOREVIC S, et al. Receiver optimization for L-DACS1[C]// IEEE/AIAA 28th Digital Avionics Systems Conference. Orlando, FL:IEEE, 2009: 4. B. 1-1-4. B. 1-12. |
| [8] | BRANDES S, EPPLE U, SCELL M. Compensation of the impact of interference mitigation by pulse blanking in OFDM systems[C]//IEEE Global Telecommunications Conference. Honolulu, HI: IEEE, 2009: 1-6. |
| [9] | EPPLE U, SHUTIN D, SCHELL M. Mitigation of impulsive frequency-selective interference in OFDM based systems[J]. IEEE Wireless Communications Letters,2012, 1 (5) : 484-487. DOI: 10.1109/WCL.2012.070312.120378 |
| [10] | LI Q, ZHANG J, XIE J, et al. Iterative interference mitigation and channel estimation for LDACS1[C]// 2014 IEEE/AIAA 33rd Digital Avionics Systems Conference (DASC 2014). Colorado:IEEE, 2014: 3B2-1-3B2-11. |
| [11] | DOVIS F, SELLONE F. Smart antenna system design for airborne GSM base-stations [C]//2000 IEEE Proceedings of the Sensor Array and Multichannel Signal Processing Workshop.Cambridge, MA: IEEE, 2000:pp. 429-433. |
| [12] | MONDIN M, DOVIS F, MULASSANO P. On the use of HALE platforms as GSM base stations[J]. IEEE Personal Communications,2001, 8 (2) : 37-44. DOI: 10.1109/98.918091 |
| [13] | AVAGNINA D, DOUIS F, GHIG LIONE A, et al. Wireless networks based on high-altitude platforms for the provision of integrated navigation/communication services[J]. IEEE Communications Magazine,2002, 40 (2) : 119-125. DOI: 10.1109/35.983918 |
| [14] | KARAPANTAZIS S, PAVLIDOU F. Broadband communications via high-altitude platforms: a survey[J]. IEEE Communications Surveys & Tutorials,2005, 7 (1) : 2-31. |
| [15] |
刘海涛, 刘亚洲, 成玮, 等. 联合正交投影与盲波束形成的干扰抑制方法[J].
系统工程与电子技术,2015, 37 (8) : 1180-1186.
LIU H T, LIU Y Z, CHENG W, et al. Interference mitigation method based on subspace projection and blind adaptive beamforming[J]. Systems Engineering and Electronics,2015, 37 (8) : 1180-1186. |
| [16] |
刘海涛, 刘亚洲, 张学军. 联合正交投影与CLEAN的测距仪脉冲干扰抑制方法[J].
信号处理,2015, 31 (5) : 536-543.
LIU H T, LIU Y Z, ZHANG X J. DME impulse interference mitigation method based on subspace projection and CLEAN algorithm[J]. Journal of Signal Processing,2015, 31 (5) : 536-543. |
| [17] |
毛维平, 李国林, 谢鑫. 均匀圆阵相干信源二维波达方向估计[J].
系统工程与电子技术,2013, 35 (8) : 1596-1601.
MAO W P, LI G L, XIE X. 2D-DOA estimation of coherent signals based on uniform circular array[J]. Systems Engineering and Electronics,2013, 35 (8) : 1596-1601. |
| [18] | HAAS E. Aeronautical channel modeling[J]. IEEE Transactions on Vehicular Technology,2002, 51 (2) : 254-264. DOI: 10.1109/25.994803 |
 2016, Vol. 48
2016, Vol. 48


