以IEEE 802.15.4标准为底层技术的ZigBee技术具有高可靠性、低功耗以及低成本等优势[1-3],广泛应用于电力系统、火灾预警、智能农业、智能交通、现代化军事以及智能家居等领域[4-6]. ZigBee树型路由ZTR(ZigBee Cluster-Tree routing)算法由于没有任何路由发现和低的存储耗能而被广泛应用,但选择路径不是最优的.
国内外学者对无线传感器网络路由算法研究较多,但是针对ZigBee网络树型路由算法研究较少. Taehong Kim等[7]提出了采用邻居表改进的最短ZigBee路由改进算法,利用ZigBee网络路由分配机制和父子节点之间的关系,选择出最短路径,但是选择的路径未考虑邻居节点的剩余能量和网络的拥塞程度,会造成网络传输的拥堵或者因节点过度消耗能量而成为失效节点. Wanzhi Qiu等[8]提出一种增强型的ZigBee路由算法,除利用父子节点之间的链路关系外,还利用一跳范围内的邻居表来寻找最短路径,同样存在未考虑节点的剩余能量问题. Atefeh Khatiri等[9]提出一种能量高效的路由(Energy shortcut tree routing,ESTR)算法,考虑通信链路的品质指示、跳数以及节点的忙碌状态,通过权重因子来综合加权选择最优路径,但权重因子不容易选择,很容易陷入局部最优. L.K. Wadhwa等[17]提出一种通过分担数据量多路径传输的优化ZigBee路由算法,在一定程度上虽然避免了网络的拥塞,但并未降低平均网络延时.
随着认知技术在无线传感器网络WSN(Wireless sensor network)中的应用逐渐扩大,MOUGY[10]和SULEIMAN Z等[11]提出的认知路由协议,已被用来提高网络性能.传感器节点性能取决于处理、存储和能量3个因素,其中能量是最需要着重考虑的.能量路由试图使能耗最小化,但一个节点可能同时被多条路径选择,可能导致其利用率过高,从而使得其为失效.因此,本文在选择出最短路径的同时,还兼顾了节点的忙碌状态和节点的剩余能量,通过对ZigBee网络节点能量的认知过程,及时启用备用节点.
1 ZigBee路由算法 1.1 ZigBee地址分配机制在IEEE802.15.4标准中,协调器通过3个重要参数控制已加入ZigBee网络的传感器节点,分别是Lm(ZigBee网络最大深度)、Cm(父节点最多可连接的后裔节点数),Rm(ZigBee网络最大可连接路由节点数). Cskip(d)用来计算Cluster-Tree算法的地址偏移量[12-14],即
| $ {C_{{\rm{skip}}}}\left( d \right) = \left\{ {\begin{array}{*{20}{l}} {1 + {C_m} \cdot \left( {{L_m} - d - 1} \right),}&{{R_m} = 1;}\\ {\frac{{1 + {C_m} - {R_m} - {C_m} \cdot R_m^{{L_m} - d - 1}}}{{1 - {R_m}}},}&{{\rm{otherwise}}.} \end{array}} \right. $ | (1) |
式中:Ai为ZigBee网络中协调器或路由节点分配给第i个路由节点的地址,Ak为ZigBee网络中协调器或者路由节点分配给第k个终端节点的地址.
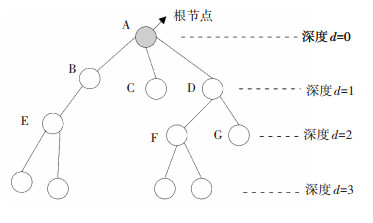
1.2 Cluster-Tree路由算法由ZigBee网络分配机制可知,ZTR算法数据传输方向可分为向上传输和向下传输,逻辑树结构如图 1所示.如果节点地址满足D < A < D+Cskip (d-1),则说明地址为A的节点是地址为D节点的子节点,则下一跳(NextHop)邻居节点的地址Na计算公式为[15-16].
| $ {N_a} = \left\{ {\begin{array}{*{20}{l}} {A, }&{{\rm{End}}\;{\rm{Devices;}}}\\ {1 + D + \left| {\frac{{A-\left( {1 + D} \right)}}{{{C_{{\rm{skip}}}}\left( d \right)}}} \right|, }&{{\rm{Otherwise}}{\rm{.}}} \end{array}} \right. $ |
|
图 1 逻辑树结构 Figure 1 The logical tree structure |
在ZigBee无线传感器网络中,单跳范围内可以直接相互通信的节点称为邻居节点,每个节点都维护其邻居表.邻居表主要由邻居节点PAN标识符、邻居节点IEEE扩展地址、邻居节点网络地址、邻居节点的类型(RFD或FFD)、邻居节点与当前节点之间的关系以及邻居节点的剩余能量等组成[17],其结构如图 2所示.由ZigBee路由分配机制可知,ZigBee树型路由算法只能向上或向下传输,虽然网络中存在节点邻居表,但是数据实际传输时并未充分利用其优势.因此,本文借助邻居表进行路径选择,以降低平均网络延时,进一步提高ZigBee网络的性能.

|
图 2 邻居表的结构 Figure 2 The neighbor table structure |
由ZigBee路由分配机制可知,节点加入网络时会自动建立邻居表.本文提出的算法在IEEE802.15.4标准框架下,利用节点感知地址信息和邻居表选择最佳路由策略,通过对ZigBee网络节点能量的认知,及时启用备用节点. EZTR算法的优化,不但降低节点的转发跳数,而且还保证了IEEE802.15.4标准的体系化. EZTR算法流程如图 3所示.

|
图 3 EZTR算法流程图 Figure 3 EZTR algorithm flowchart |
当节点接收到数据包时,首先判断自己是否为目的节点,若是则直接接收数据,否则,根据节点维护的邻居表(含有节点地址信息、单跳范围内节点的关系、邻居节点的剩余能量等信息)判断目的节点是否为当前节点的子节点、父节点或邻居节点,若目的节点与当前节点是父子关系,直接按照树型结构向上或向下传递数据包,否则向下一跳节点发送带有目的地址的路由请求,采用轮询方式计算所有邻居节点到达目的节点的跳数,利用每个节点感知的地址信息选择最短路径.若网络中存在多条最短路径,选取剩余能量最多的节点作为下一跳邻居节点.判断在最少跳数的路径中节点是否为空闲状态,若路径中所有节点均处于空闲状态,选择此路径为最优路径;若在最优路径中存在能量过低的节点,使用备用节点代替,通过设置标志位(Flag)实现节点与备用节点间的替换. Flag=0表示能量过低的节点,Flag=1表示忙碌节点,Flag=2表示备用节点.此后的中继节点转发也依据此方式进行,不断更新节点维护的单跳范围内的邻居表,直到数据发送到目的节点.
为了尽可能减小因备用节点影响ZigBee网络的拓扑结构,备用节点选取与原节点直接相邻的节点,即选择单跳范围内节点作为备用节点,同时为了避免备用节点再次成为失效节点,选取单跳范围内剩余能量最多的节点作为备用节点,采用轮询的方式将原节点的信息全部复制给备用节点.如果在一段时间内没有收到“低能量节点”请求消息或“节点忙碌”请求消息,则备用节点进入睡眠状态,降低因备用节点的存在而使网络付出更多的能量代价.
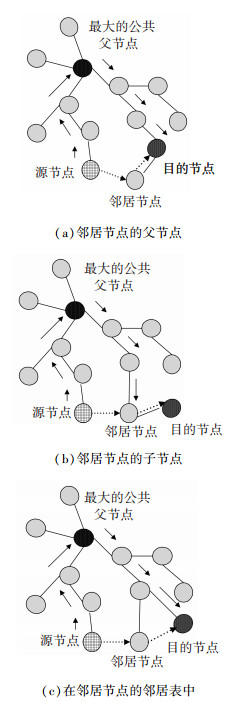
图 4以EZTR算法路由选择为例分析说明ZTR算法和EZTR算法的传输机制,其中实线代表ZTR算法的路由实现过程,虚线代表EZTR算法的路由实现过程.从图中可以看出,与ZTR算法相比,图 4(a)节省4跳,图 4(b)节省5跳,图 4(c)节省4跳.由于传统的ZigBee路由算法完全按照父子之间的关系选择最短路径,所以转发数据需要公共父节点的参与,而EZTR算法利用邻居表和节点地址进行路径选择,不需要公共父节点的参与,因此降低了转发跳数.另外,从图中也可以看出,越靠近最大公共父节点的节点转发数据越频繁,能量很快耗尽,从而很快就变为失效节点,可能造成网络的中断.
|
图 4 ZigBee树路由和EZTR树路由 Figure 4 ZigBee tree routing and EZTR tree routing |
利用每个节点感知的地址信息选择最短路径.为了避免ZigBee网络的环路响应,该算法通过树型结构来计算下一跳节点到目的节点之间的路由开销.
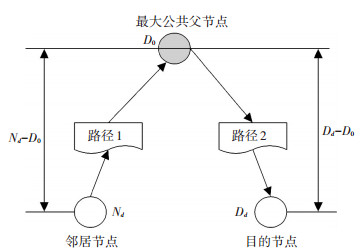
节点跳数的计算方法为:找到最大的公共父节点的地址,然后借助最大公共父节点的深度计算EZTRN节点到目的节点之间的跳数,如图 5所示.跳数计算公式和最少跳数选取公式分别为
| $ \begin{array}{l} {\rm{Count}} = \left( {{N_d}-{D_o}} \right) + \left( {{D_d}-{D_o}} \right) = {N_d} + {D_d}-2{D_o}, \\ \min \_{\rm{count}} = \min \left\{ {{\rm{counti}}} \right\}, i \in \left\{ {1, 2, 3, \cdots, n} \right\}. \end{array} $ |
|
图 5 源节点和目的节点之间的路由消耗 Figure 5 Routing consumption between the source node and the destination node |
式中:count为跳数,Nd为邻居节点的深度,Dd为目的节点的深度,D0为最大公共父节点的深度,最少跳数为min_count,counti为第i条邻居节点到目的节点转发跳数.其中寻找最大公共父节点的方法为:根据ZigBee路由分配机制,当节点的深度小于网络最大深度(Lm)时,依据式(1)采用轮询的方式来实现.
2.3 低能量节点判断在WSN实际应用中,某些节点(如图 4中最大公共父节点附近的节点)频繁使用,导致能量过度消耗,而其他节点被闲置,会造成节点能量不均衡,因此部分节点因过早失效而引起在最优路径下的“能量空洞”现象,可能会导致网络数据传输中断或出现网络拥塞现象.
判断一个节点是充足能量节点还是低能量节点,其依据是节点的剩余能量与能量阈值(最小剩余能量)的关系.若节点剩余能量低于最小剩余能量,则为低能量节点,否则为充足能量节点.由于节点的剩余能量随着迭代次数的增加而逐渐减少.因此,最小剩余能量公式的选取需要动态变化,尽量使最小剩余能量递减缓慢.根据已有的数学知识,EZTR算法在能量公式改进中采取两种措施,一是通过对前一次的剩余能量开平方处理,二是设置参数θ.由于IEEE 802.15.4规定协调器的地址为0且分式的分母不能为0,因此在控制节点深度di与剩余能量成反比的同时,节点深度也需要加上1.当迭代次数为k=1,di=0时,E1=θ
| $ {E_{\min }} = \frac{1}{k} \times \sqrt {{E_0}} \times \frac{1}{{{d_i} + 1}} \times \theta . $ |
式中:E0为节点的初始能量,di为网络中第i个节点的深度.
3 仿真及分析 3.1 搭建ZigBee能量模型ZigBee网络数据传输的总能耗E包括ET(k,d)为节点A发送k bit数据包到节点B所需能耗和ER(k)为节点B接收k bit数据包所需能耗,d为两个节点之间的通信距离. ZigBee能量模型如图 6所示.

|
图 6 能量模型 Figure 6 Energy model |
节点发送k bit数据包消耗的能量为
| $ {E_T}\left( {k, d} \right) = k{E_{{\rm{elec}}}} + {\varepsilon _{{\rm{amp}}}}k{d^3}. $ |
式中:Eelec为发射电路发送1 bit数据包的能耗,εamp为发射放大器处理1 bit数据包传输单位距离所需要的能耗.假设接收电路与发射电路有相同的能量消耗,则接收k bit数据包的能量消耗为
| $ {E_R}\left( k \right) = k{E_{{\rm{elec}}}}. $ |
采用此模型,则一个路由节点的总能耗为
| $ E = {E_T}\left( {k, d} \right) + {E_R}\left( k \right) = 2{E_{{\rm{elec}}}}kM + {\varepsilon _{{\rm{amp}}}}k\sum\limits_{m = 1}^M {d_m^3} . $ |
式中M和dm分别是路由节点的跳数和第m跳的发送距离.
3.2 评价指标定义定义1 分组递交率指节点成功接收到数据分组的个数与节点发送数据的个数的比值,反映了网络的链路质量.设PDR为分组递交率, 则
| $ \overline {{\rm{PDR}}} = \frac{{\sum\limits_{i = 0}^N {{R_i}} }}{{\sum\limits_{k = 0}^M {{S_k}} }}. $ |
式中: Ri表示第i个节点成功接收的数据分组的个数,Sk表示第k个节点发送数据分组的个数.
定义2 平均跳数指介质访问控制MAC(Medium Access Control)层转发数据包的个数与源节点发送数据包的个数的比值,衡量无线传感网络能耗和实时性的一个重要指标.设N_ave为平均跳数为, 则
| $ \bar N\_{\rm{ave = }}\frac{{{M_{{\rm{MAC}}}}}}{{{M_{{\rm{sour}}}}}}. $ |
式中: NMAC为MAC层转发N个数据包,因为MAC层的作用是确认数据传送和接收; Msour为源节点发送M个数据包.
定义3 平均网络延时指传送数据包所需的时间,反映了数据通信的快慢,影响在线监测系统的实时性.设
| $ \overline {{T_d}} = \frac{{\sum\limits_{i = 0}^N {{T_r}\left( i \right)-{T_s}\left( i \right)} }}{{{M_{{\rm{des}}}}}}. $ |
式中:Tr(i)为接收第i个数据包的时刻,Ts(i)为发送第i个数据包的时刻,Mdes为目的节点成功接收M个数据包.
定义4 剩余能量百分比指网络运行结束后所有节点的剩余能量与网络初始时所有节点的能量的比值,间接反映了ZigBee网络节点能耗的大小,是网络节能的重要标志,影响WSN网络的生存周期.设RER为剩余能量百分比, 则
| $ \overline {{\rm{RER}}} = \frac{{\sum\limits_{i = 0}^N {{E_i}} }}{{M \cdot {E_0}}}. $ |
式中: Ei为第i个节点剩余能量,E0为ZigBee网络中M个节点的初始能量.
3.3 NS2.35仿真参数设置为了验证EZTR算法的性能,利用IEEE 802.15.4 PHY/MAC协议进行ZTR(经典的ZigBee树型路由)、EZTR(本文提出的优化树型路由)以及参考文献[9]提出的ESTR(能量高效的树型路由)进行网络层协议仿真.将节点随机分布在100 m×100 m区域中,使用cbrgen产生CBR数据流,实验发送数据包的大小为70 bytes,CBR数据流的带宽为1 Mbit/s.
实验采用表 1所列的节点仿真参数,利用awk测试脚本提取Trace文件中的节点数据.仿真动画效果如图 7所示. NAM动画仿真之后,自动生成一个以.tr为格式的trace跟踪文件,该文件可以记录ZigBee节点整个通信过程,使用AWK语言获取需要的数据信息.
|
图 7 仿真动画 Figure 7 Simulation animation |
| 表 1 节点仿真参数 Table 1 Simulation parameters |
分组递交率随节点数目的变化曲线如图 8所示. EZTR在分组递交率方面优于ZTR和ESTR,EZTR、ZTR及ESTR的整体分组递交率分别为85.64%、71.81%及80.30%,相应提高了13.83%和5.34%,主要是由于本文提出的EZTR算法考虑了链路的忙碌状态和节点的剩余能量,如果存在能量过低的节点,有可能造成丢包现象;如果链路处于忙碌状态,EZTR算法引入备用节点,避免因数据堵塞而造成丢包现象.其次,该算法按照树型结构计算路由跳数,避免了网络的环路响应.最后,EZTR算法选择的路径是最短的,减少了队列的延时,一定程度上也提高了网络的分组递交率.

|
图 8 节点的平均分组递交率随节点数目变化 Figure 8 Average PDR with the number of nodes changes |
节点的平均跳数随网络节点数目的变化曲线如图 9所示.随着传感器节点的不断加入,网络拓扑结构越复杂. 3种算法的转发跳数均增加,但是ZTR算法跳数远多于ESTR和EZTR算法,EZTR、ZTR及ESTR的整体跳数分别为4.99、6.92及5.39,相应降低了27.78%和7.42%.由于EZTR算法在确保链路为空闲状态传输数据和采用备用节点的前提下,选择EZTRN节点到目的节点最少跳数,因此采用EZTR算法转发跳数低于ZTR和ESTR的跳数.

|
图 9 节点的平均跳数随节点数目变化 Figure 9 Mean hop with the number of nodes changes |
随着传感器节点数目的增加,不但节点跳数增加,平均网络延时也不断增加. 3种算法的平均网络延时随网络节点数目变化曲线如图 10所示.从图 10可以看出,由于EZTR算法不但考虑转发跳数和链路忙碌状态,还较大幅度地减少转发跳数,虽然在一定程度上因增加算法的复杂度导致程序运行时间增加,但该算法优化节点传输的路径,在实时性方面仍然优于ZTR和EZTR算法,EZTR、ZTR及ESTR的整体时延分别为0.017、0.031及0.022,相应降低了45.01%和22.68%,提高无线传感网络在线监测的实时性.

|
图 10 平均网络延时随节点数目变化 Figure 10 Mean delay with the number of nodes changes |
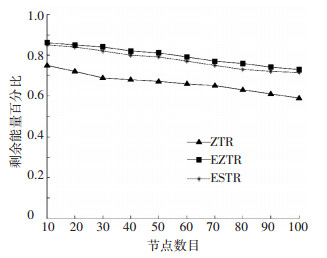
节点平均剩余能量百分比随节点数目变化如图 11所示. EZTR、ZTR及ESTR的整体剩余能量百分比分别为0.79、0.67及0.74,相应提高了19.85%和6.75%,主要是由于EZTR算法大幅度降低了节点的转发跳数,虽然一定程度上增加了因算法复杂度提高而消耗一部分能量,但是由于该算法优化了节点转发路径,总体上仍然节约ZigBee网络的能耗.
|
图 11 节点平均剩余能量百分比随节点数目变化 Figure 11 The average percentage of residual energy with the number of nodes changes |
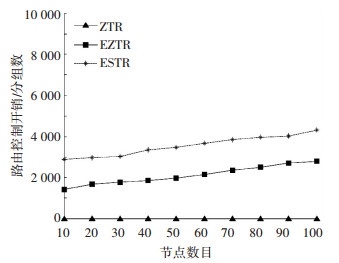
为了客观公正的评价EZTR算法的性能,对ZTR算法和EZTR算法在路由控制开销方面进行了仿真实验,路由控制开销仿真结果如图 12所示.从图中可以看出,ZTR算法没有任何路由控制开销,是因为ZTR算法在数据通信时只根据父子节点之间的关系进行数据的传递. ESTR算法与EZTR算法相比,在寻找最优路径时,由于需要额外考虑链路品质因数和合理选取综合加权因子等因素,路由控制开销多于EZTR算法.
|
图 12 路由控制开销随节点数目的变化 Figure 12 Routing overhead with the number of nodes changes |
本文利用单跳范围内的邻居节点和父子节点之间的关系,在认知视角下提出一种能量感知的ZigBee树型路由(EZTR)算法.该算法不但在IEEE802.15.4标准体系化框架下能够选出最短路径,还兼顾了节点的忙碌状态和节点的剩余能量,通过对ZigBee网络节点能量的认知,当网络中所选路径存在低能量节点时,及时启用备用节点. NS2仿真结果表明,EZTR算法的性能优于ESTR、ZTR算法.由于经典的树型路由(ZTR)算法在数据传输时只在父子节点之间进行数据传输,无任何路由控制开销,而EZTR算法需感知最短路径,与ZTR算法相比需要付出增加路由控制开销和占用传输带宽等代价,同时会增加节点的存储和计算能力,该算法的性能还有待于进一步优化.
| [1] |
庞毅, 王超, 孙青林, 等. Zigbee网络环状分层方法的仿真与实现[J].
哈尔滨工业大学学报,2013, 45 (3) : 123-128.
PANG Yi, WANG Chao, SUN Qinglin, et al. Simulation and realization of zigbee network annular stratification[J]. Journal of Harbin Institute of Technology,2013, 45 (3) : 123-128. |
| [2] |
张云洲, 蒋培, 高亮, 等. 基于DSP和双目视觉的多媒体传感器网络节点设计与实现[J].
通信学报,2014, 35 (12) : 210-216.
ZHANG Yunzhou, JIANG Pei, GAO Liang, et al. Design and implementation of wireless multimedia sensor network node based on DSP and binocular vision[J]. Journal on Communications,2014, 35 (12) : 210-216. |
| [3] | SHARIFF F, RAHIMA N A, HEW W P. Zigbee based data acquisition system for online monitoring of grid connected photovoltaic system[J]. Expert Systems with Applications,2015, 35 (42) : 1730-1742. |
| [4] | SANG Shengbo, FAN Xiao, TANG Xiaoliang, et al. Portable surface stress biosensor test system based on ZigBee technology for health care[J]. Biotechnology & Biotechnological Equipment,2015, 45 (29) : 798-804. |
| [5] | NIU Jianwei, WANG Bowei, SHU Lei, et al. An energy-efficient indoor localization system using ZigBee radio to detect WiFi fingerprints[J]. Selected Areas in Communications,2015, 33 (7) : 1431-1442. DOI: 10.1109/JSAC.2015.2430171 |
| [6] | ChEN S K, KAO T, CHAN C T, et al. A reliable transmission protocol for ZigBee-based wireless patient monitoring[J]. IEEE Trans Information Technology in Biomedicine,2012, 16 (1) : 6-16. DOI: 10.1109/TITB.2011.2171704 |
| [7] | KIM T, KIM S H, YANG J, et al. Neighbor table based shortcut tree routing in ZigBee wireless networks[J]. IEEE Transcations on Parallel and Distributed Systems,2014, 25 (3) : 706-715. DOI: 10.1109/TPDS.2014.9 |
| [8] | QIU Wanzhi, PENG Hao. Enhanced tree routing for wireless sensor networks[J]. Ad Hoc Networks,2009, 39 (7) : 638-650. |
| [9] | KHATIRI A, MIRJALITY G. Energy Efficient Shortcut Tree Routing in ZigBee Networks[C]//Communication Systems and Networks, 2012 Fourth International Conference on Computational Intelligence. Harbin: ACM, 2012:117-122. |
| [10] | MOUGY A E, EI Z H, IBNKAHLA, M. Cognitive approaches to routing in wireless sensor networks[C]//IEEE Global Telecommunications Conference.2010. https://www.researchgate.net/profile/Elyes_Bdira/publication/224211072_Cognitive_Approaches_to_Routing_in_Wireless_Sensor_Networks/links/00b4951b059e4d2d2a000000.pdf |
| [11] | SULEIMAN Z, NORSHEILA F. Reliable geographical forwarding in cognitive radio sensor networks using virtual clusters[J]. Sensors,2014, 14 (5) : 8996-9026. DOI: 10.3390/s140508996 |
| [12] |
钱志鸿, 朱爽, 王雪. 基于分簇机制的ZigBee混合路由能量优化算法研究[J].
计算机学报,2013, 36 (3) : 485-493.
QIAN Zhihong, ZHU Shuang, WANG Xue. An cluster-based ZigBee routing algorithm for Network energy optimization[J]. Chinese Journal of Computers,2013, 36 (3) : 485-493. |
| [13] | HUANG Y K, PANG A C, HSIV PC, et al. Distributed throughput optimization for ZigBee cluster-tree networks[J]. IEEE Trans. Parallel and Distributed Systems,2012, 23 (3) : 513-520. DOI: 10.1109/TPDS.2011.192 |
| [14] | KIM T, KIM D, PAK N, et al. Shortcut tree routing in ZigBee networks[C]//2007 2nd International Symposium on Wireless Pervasive Computing. 2007:42-47. |
| [15] | YANG Guisong, WANG Zhongjie, WU Chunxue, et al. One-hop expansion ETR protocol for wireless sensor networks[J]. Journal of Convergence Information Technology,2012, 7 (11) : 169-178. DOI: 10.4156/jcit |
| [16] | KWON K, HA M, KIM T, et al. The stateless point to point routing protocol based on shortcut tree routing algorithm for IP-WSN[C]//Proceedings of 2012 International Conference on the Internet of Things. 2012:167-174. |
| [17] | WADHWA L K, RASHMI R S, PRIYE V. Extended shortcut tree routing for ZigBee based wireless sensor network[J]. Ad Hoc Networks,2016, 37 (2) : 295-300. |
 2016, Vol. 48
2016, Vol. 48


