2. 海军装备研究院,北京 100073
2. Naval Academy of Armament, Beijing 100073, China
自适应波束形成技术能够在期望信号方向形成恒定的增益,在干扰方位上形成零陷,被广泛应用于雷达、声纳和移动通信等领域[1-3].常用的波束形成器如最小方差无失真响应(MVDR,又名Capon)波束形成器,是建立在阵列对期望信号导向矢量准确已知的情况下.在实际环境中,当期望信号导向矢量出现失配时,波束形成器可能会在期望信号方向形成零陷,出现信号“自消”的现象,导致阵列输出性能急剧下降[4-5].同时当干扰快速运动或载体平台的振动,以及自适应权值更新速度相对较慢等,出现加权矢量训练数据与应用数据失配时[6],干扰有可能移出零陷位置,得不到有效地抑制,也会造成波束形成器的性能明显下降.
针对导向矢量失配引起输出性能急剧下降的问题,近年来出现了很多稳健的波束形成算法[7-11],但这些算法存在参数选择困难[7-8]、计算量较大[9-11]和无法抑制快速运动的干扰[12]的缺点.针对快速运动的干扰可能移出零陷的问题,零陷展宽技术能够在干扰方位处形成较宽的零陷,从而有效抑制快速运动的干扰[13-16].协方差矩阵锐化可以零陷展宽,但会使得零陷深度变浅,阵列增益下降[13-14].最近出现的基于子空间投影[15]和基于线性约束[16]的零陷展宽方法,可以在预定的区域展宽零陷,得到较深的零陷,但都需要知道干扰的大致来波方向这一先验信息,且缺乏对期望信号导向矢量大角度失配的稳健性.文献[17]中提出既能抗导向矢量失配又能抑制快速运动干扰的算法,但该方法需同时知道协方差矩阵的失配量和导向矢量的失配量,且其输出性能受约束参数的影响较大.
本文通过投影变换预处理技术扩展干扰入射方向,进而展宽零陷宽度并加深零陷深度,再根据期望信号入射的大致方位,对波束主瓣的幅度响应进行约束,在期望信号入射的大致方位形成稳定的响应幅度,达到抗导向矢量失配的目的,提高了波束形成器在复杂环境下的抗干扰性能.
1 阵列信号模型 1.1 MVDR波束形成器设有一个期望信号从θ0方向入射到N元间距为d的均匀直线阵(ULA)上,P个干扰从θk, k=1, 2, …, P方向入射,则阵列接收数据X(t)可以表示为
| $ \boldsymbol{X}\left( t \right) = \boldsymbol{AS}\left( t \right) + \boldsymbol{N}\left( t \right). $ |
式中:X(t)=[x1(t), x2(t), …, xN(t)]T为N×1阵列数据向量;S(t)=[s0(t), s1(t), …, sP(t)]T,sk(t)为t时刻第k个信号的复包络;N(t)=[n1(t), n2(t), …, nN(t)]T为t时刻N×1阵列天线白噪声向量;A为阵列的流形矩阵,A=[a(θ0), a(θ1), …, a(θP)],对于均匀直线阵,a(θP)=
| $ \boldsymbol{R} = E\left\{ {\boldsymbol{X}\left( t \right){\boldsymbol{X}^H}\left( t \right)} \right\} = \boldsymbol{A}{\boldsymbol{R}_s}{\boldsymbol{A}^H} + \sigma _n^2\boldsymbol{I}. $ |
式中:E{·}表示求数学期望,Rs表示期望信号加干扰的协方差矩阵,σn2是噪声功率,I是N维单位矩阵.
在实际计算中,阵列接收信号的协方差矩阵经常是用有限次的快拍数据估计值来代替,可以写为
| $ \mathit{\boldsymbol{\hat R}} = \frac{1}{K}\sum\limits_{n = 1}^K {\mathit{\boldsymbol{X}}\left( n \right){\mathit{\boldsymbol{X}}^H}\left( n \right), } $ | (1) |
式中K为快拍数.标准MVDR波束形成器的自适应加权矢量w表示为
| $ \mathit{\boldsymbol{w}} = \frac{{{{\mathit{\boldsymbol{\hat R}}}^{-1}}\mathit{\boldsymbol{\bar a}}\left( {{\theta _0}} \right)}}{{{{\mathit{\boldsymbol{\bar a}}}^H}\left( {{\theta _0}} \right){{\mathit{\boldsymbol{\hat R}}}^{-1}}\mathit{\boldsymbol{\bar a}}\left( {{\theta _0}} \right)}}, $ |
式中Ȓ-1表示对协方差矩阵Ȓ求逆,ā(θ0)表示估计的期望信号导向矢量.
阵列波束形抗干扰的性能可以通过输出RSIN进行衡量,RSIN定义为阵列天线输出的期望信号的功率与输出的干扰信号功率加上噪声功率之和的比值,表达式为
| $ \begin{array}{c} {R_{{\rm{SIN}}}} = \frac{{\sigma _s^2{{\left| {{\mathit{\boldsymbol{w}}^H}\mathit{\boldsymbol{a}}\left( {{\theta _0}} \right)} \right|}^2}}}{{{\mathit{\boldsymbol{w}}^H}{\mathit{\boldsymbol{R}}_{i + n}}\mathit{\boldsymbol{w}}}} = \\ \frac{{\sigma _s^2{{\left| {{\mathit{\boldsymbol{w}}^H}\mathit{\boldsymbol{a}}\left( {{\theta _0}} \right)} \right|}^2}}}{{{\mathit{\boldsymbol{w}}^H}\left( {\sum\limits_{k = 1}^p {\sigma _k^2{\mathit{\boldsymbol{a}}_k}\mathit{\boldsymbol{a}}_k^H + \sigma _n^2{\mathit{\boldsymbol{I}}_{N \times N}}} } \right)\mathit{\boldsymbol{w}}}}. \end{array} $ |
式中:Ri+n表示干扰加噪声的协方差矩阵,σs2表示输入的期望信号功率,σk2表示第k个干扰的功率.
标准MVDR波束形成器在理想情况下具有良好的干扰抑制性能和较高的输出RSIN,但是当期望信号导向矢量a(θ0)估计失配时,MVDR波束形成器的输出性能会急剧下降.当环境中存在快速运动的干扰,自适应权值数据来不及更新时,干扰很有可能移出零陷位置而不能被有效抑制,MVDR波束形成器的输出性能也会出现明显下降[18].
2 本文算法针对以上存在问题,本文提出基于投影变换技术与主瓣幅度约束结合的稳健波束形成方法.首先利用零陷展宽投影变换技术与对角加载技术构造一个新的协方差矩阵,再对波束主瓣区域进行幅度响应约束,在期望信号方位附件形成平顶状的波束图.应用半正定秩松弛方法将本文约束优化问题松弛为一个半正定优化问题,利用凸优化理论得到最优解.
2.1 零陷展宽投影变换技术设定Θ为干扰大致的方位区间,Θ可以通过对阵列接收的前K/2快拍数据进行空间谱估计得到,值得注意的是,Θ不需要估计的十分准确,只需大概估计出来即可.在Θ区域内每0.1°取一个插值点,共设有L个插值点.若存在多个干扰,设Θ1,Θ2, …, Θp(p=1, 2, 3, …)分别为干扰1、干扰2等对应的大致方位区间,p为干扰的个数.天线阵列在这些插值点的导向矢量表示为a(θi), i=1, 2, …, L.构建导向矢量的相关矩阵Cθ为
| $ \begin{array}{c} {\mathit{\boldsymbol{C}}_\theta } = \int_{\mathit{\Theta }1} {\mathit{\boldsymbol{\bar a}}\left( \theta \right)} {{\mathit{\boldsymbol{\bar a}}}^H}\left( \theta \right){\rm{d}}\theta {\rm{ + }}\int_{\mathit{\Theta }2} {\mathit{\boldsymbol{\bar a}}\left( \theta \right)} {{\mathit{\boldsymbol{\bar a}}}^H}\left( \theta \right){\rm{d}}\theta \cdots + \\ \int_{\mathit{\Theta }p} {\mathit{\boldsymbol{\bar a}}\left( \theta \right)} {{\mathit{\boldsymbol{\bar a}}}^H}\left( \theta \right){\rm{d}}\theta . \end{array} $ |
对Cθ进行特征分解,得到
| $ {\mathit{\boldsymbol{C}}_\theta } = \sum\limits_{k = 1}^N {{\mu _{{\theta _k}}}{{\mathit{\boldsymbol{\bar v}}}_{{\theta _k}}}\mathit{\boldsymbol{\bar v}}_{{\theta _k}}^H, {\mu _{{\theta _1}}} \ge {\mu _{{\theta _2}}} \ge \cdots \ge } {\mu _{{\theta _N}}}, $ | (2) |
式中μθ表示特征值,υθk表示与特征值μθk相对应的特征向量.在N个特征值中,提取出其中M个比较大的特征值,则有
| $ \sum\limits_{k = M + 1}^N {{\mu _{{\theta _k}}}} /\sum\limits_{k = 1}^N {{\mu _{{\theta _k}}}} \le \varepsilon, $ |
式中ε是一个预定的常数,它将决定所选取特征向量的个数,也就是基向量的个数.以Cθ的M个大特征值对应的特征向量作为基向量,定义基向量张成的空间P1为
| $ {P_1} = {\rm{span}}\left\{ {{{\mathit{\boldsymbol{\bar v}}}_{{\theta _1}}}\mathit{\boldsymbol{, }}{{\mathit{\boldsymbol{\bar v}}}_{{\theta _2}}}, \cdots, {{\mathit{\boldsymbol{\bar v}}}_{{\theta _M}}}} \right\}. $ |
利用选定的基向量形成投影算子,定义投影算子T为
| $ \mathit{\boldsymbol{T}}\sum\limits_{k = 1}^M {{{\mathit{\boldsymbol{\bar v}}}_{{\theta _k}}}\mathit{\boldsymbol{\bar v}}_{{\theta _k}}^H.} $ |
投影算子T的计算是一个离线计算过程,存储到系统中可以直接调用.利用T对阵列接收数据X(n)进行投影处理,则经投过影变换后的阵列接收数据
| $ \widetilde {\mathit{\boldsymbol{\bar X}}}\left( n \right) = TX\left( n \right). $ |
根据式(1),投影变换后的阵列接收的协方差数据矩阵
| $ \hat{\mathrm{\mathit{\pmb{{\bar{R}}}}}}= \frac{1}{K}\sum\limits_{n = 1}^K {\widetilde {\mathit{\boldsymbol{\bar X}}}\left( n \right){{\widetilde {\mathit{\boldsymbol{\bar X}}}}^H}\left( n \right)} = \mathit{\boldsymbol{T\hat R}}{\mathit{\boldsymbol{T}}^H}, $ |
从式(2)可以看到,投影变换矩阵T是由Cθ经过特征分解得到的,包含了干扰可能入射的方位信息,从而起到扩张干扰入射方向的作用,因此能够展宽波束所形成的零陷,其中Θ决定了波束零陷宽度.
2.2 协方差矩阵对角加载对协方差矩阵进行对角加载处理是提高波束形成器稳健性的常用方法[7-8],对经投影变换处理后的协方差矩阵
| $ \widetilde {\mathit{\boldsymbol{\bar R}}} = \hat{\mathrm{\mathit{\pmb{{\bar{R}}}}}} + \rho \mathit{\boldsymbol{I}} = \mathit{\boldsymbol{T\hat R}}{\mathit{\boldsymbol{T}}^H} + \rho \mathit{\boldsymbol{I}}. $ | (3) |
式中:
常规波束形成器在期望信号导向矢量出现失配时,波束主瓣不能指向期望信号的实际方向,甚至在期望信号实际方向形成零陷,波束形成器的输出性能急剧下降.因此,在期望信号的附近区域施加幅度响应约束,形成平顶状的方向图,能够降低波束形成器对期望信号导向矢量的敏感度,提高波束形成器的稳健性[19].
设Θm为期望信号来波的大致区域,即波束图的约束区域,对此区域施加如下约束:
| $ L\left( \theta \right) < \left| {{\mathit{\boldsymbol{w}}^H}\mathit{\boldsymbol{a}}\left( \theta \right)} \right| < U\left( \theta \right), \theta \in {\Theta _m}. $ | (4) |
式中L(θ),U(θ)分别为波束图约束区域幅度响应的下限值和上限值.通过施加上述约束,能够保证在Θm内,波束形成器都能够有恒定的增益,有效提高波束形成器对期望信号导向矢量的容错性.但是,约束条件L(θ) < |wHa(θ)|相对于w是一个非凸问题,导致求解困难.因此,需要将其转化为易于求解的凸优化问题,式(4)等价于
| $ {L^2}\left( \theta \right) < {\left| {{\boldsymbol{w}^H}\boldsymbol{a}\left( \theta \right)} \right|^2} < {U^2}\left( \theta \right), \theta \in {\Theta _m}. $ | (5) |
易知,|wHa(θ)|2=tr{wwHa(θ)aH(θ)}=tr{R1(θ)W},其中tr{·}表示矩阵求迹,W=wwH,R1(θ)=a(θ)aH(θ).由于W是一个半正定Hermitian矩阵,因此有
| $ \boldsymbol{W} \ge 0. $ |
同时,rank(W)=1.因此,式(5)可以写为
| $ {L^2}\left( \theta \right) < {\rm{tr}}\left\{ {{\boldsymbol{R}_1}\left( \theta \right)\boldsymbol{W}} \right\} < {U^2}\left( \theta \right), \theta \in {\Theta _m}. $ | (6) |
式(6)是一个关于W的线性优化问题,可以利用凸优化理论求解.同理,可以得到
| $ \mathit{\boldsymbol{w}}\widetilde {\mathit{\boldsymbol{\bar R}}}\mathit{\boldsymbol{w}} = {\rm{tr}}\left\{ {\mathit{\boldsymbol{w}}\widetilde {\mathit{\boldsymbol{\bar R}}}\mathit{\boldsymbol{w}}} \right\} = {\rm{tr}}\left\{ {\widetilde {\mathit{\boldsymbol{\bar R}}}\mathit{\boldsymbol{W}}} \right\} = {\rm{tr}}\left\{ {\left( {\hat{\mathrm{\mathit{\pmb{{\bar{R}}}}}} + \rho \mathit{\boldsymbol{I}}} \right)\mathit{\boldsymbol{W}}} \right\}. $ |
利用式(3)中新构造的协方差矩阵,可以得到本文所提稳健零陷展宽算法的优化问题模型:
| $ \begin{array}{c} \mathop {\min }\limits_W {\rm{tr}}\left\{ {\left( {\hat{\mathrm{\mathit{\pmb{{\bar{R}}}}}} + \rho \mathit{\boldsymbol{I}}} \right)\mathit{\boldsymbol{W}}} \right\}.\\ {\rm{s}}{\rm{.t}}.\left\{ \begin{array}{l} {\rm{tr}}\left\{ {{\mathit{\boldsymbol{R}}_1}\left( \theta \right)\mathit{\boldsymbol{W}}} \right\} > {L^2}\left( \theta \right), \theta \in {\Theta _m};\\ {\rm{tr}}\left\{ {{\mathit{\boldsymbol{R}}_1}\left( \theta \right)\mathit{\boldsymbol{W}}} \right\} < {U^2}\left( \theta \right), \theta \in {\Theta _m};\\ {\rm{rank}}\left( \mathit{\boldsymbol{W}} \right) = 1, \mathit{\boldsymbol{W}} \ge 0. \end{array} \right. \end{array} $ |
式中,约束条件rank(W)=1仍然是非凸的,但是可以将该约束条件除去[20],松弛为如下半正定的问题进行求解:
| $ \begin{array}{c} \mathop {\min }\limits_W {\rm{tr}}\left\{ {\left( {\hat{\mathrm{\mathit{\pmb{{\bar{R}}}}}} + \rho \mathit{\boldsymbol{I}}} \right)\mathit{\boldsymbol{W}}} \right\}.\\ {\rm{s}}{\rm{.t}}.\left\{ \begin{array}{l} {\rm{tr}}\left\{ {{\mathit{\boldsymbol{R}}_1}\left( \theta \right)\mathit{\boldsymbol{W}}} \right\} > {L^2}\left( \theta \right), \theta \in {\Theta _m};\\ {\rm{tr}}\left\{ {{\mathit{\boldsymbol{R}}_1}\left( \theta \right)\mathit{\boldsymbol{W}}} \right\} < {U^2}\left( \theta \right), \theta \in {\Theta _m};\\ \mathit{\boldsymbol{W}} \ge 0. \end{array} \right. \end{array} $ | (8) |
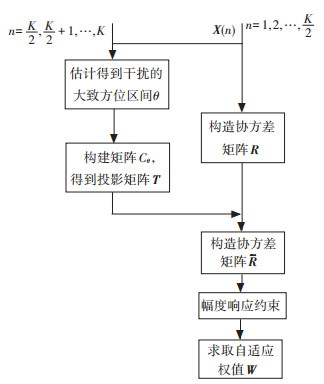
其中L(θ)=10-rdB/20,U(θ)=10rdB/20,rdB表示幅度约束的波纹值.式(8)是一个关于W的凸优化问题,可以通过内点法进行求解.求解式(8),得到的是W,需要对W进行谱分解,得到最优加权矢量w,文献[19]对如何进行谱分解有详细的论述,在此不再赘述.本文算法的基本思想如图 1所示.
|
图 1 本文算法结构图 Figure 1 Structure of the proposed algorithm |
综合以上分析,得到本文波束形成算法的求解步骤:
1) 对阵列接收的前K/2个快拍数据进行空间谱估计,得到干扰信号可能出现的方位区间Θ,构建导向矢量相关矩阵Cθ,将导向矢量的相关矩阵Cθ进行特征分解,用大特征值对应的特性矢量为基矢量得到投影变换矩阵T,将T存储起来以便离线计算.
2) 利用矩阵T对原始的协方差矩阵进行重构,得到
3) 根据期望信号的大致方位,选定幅度约束区域,建立式(8)所示的优化问题.
4) 利用内点法求解凸优化问题式(8),得到W,对W进行谱因子分解,得到最优加权矢量w.
3 仿真实验与性能分析考虑一个阵元数目为10的ULA阵,阵元间距为半波长.所加噪声为高斯白噪声,期望信号从0°方向入射,信号与干扰之间是相互独立的.所有实验结果均来自100次独立的蒙特卡罗实验.如无特别说明,仿真试验中,本文算法所选基向量个数为6个,对主瓣约束区域为[-7°, 7°],对角加载因子设为ρ=0.010,波纹大小值设为rdB=0.3,干噪比INR=30 dB,快拍数为100.
3.1 零陷展宽波束图比较仿真1 零陷加宽角度为Δθ=10°,信噪比RSN=0 dB. 2个独立干扰分别位于-40°, 50°方向,利用Capon空间谱[21]估计得到的干扰角度分别为-39°和51°,出现了1°的偏差,零陷展宽区间为[-45°, -35°]∪[45°, 55°],文献[16]中选取的特征向量个数为3个.首先设定期望信号来波方向估计无误,图 2为此时几种不同算法的波束图.

|
图 2 导向矢量准确已知时波束图的比较 Figure 2 Normalized beampattern plots with the exactly known steering vector |
从图 2中可以看到,在导向矢量准确已知时,标准MVDR波束形成器在干扰位置处形成了陡峭的零陷,零陷深度-60 dB左右.在设定零陷宽度为10°时,Mailloux方法形成的零陷宽度可以达到要求,但零陷深度较变浅,只有-50 dB左右,且旁瓣升高较为严重.文献[16]方法由于在干扰附近方位施加了置零约束,零陷深度比Mailloux方法深,达到-60 dB左右.本文算法所形成的零陷宽度十分明显,而且零陷深度超过-70 dB,同时本文算法有更低的旁瓣,两侧旁瓣平均值达到-20 dB左右,由于在[-7°, 7°]方位区域施加了幅度响应约束,本文算法在约束区域(图中箭头所示)形成了平坦的波束图.
3.2 抗波前扰动失真和局部相干散射性能仿真与分析考察本文算法在出现信号波前扰动失真和局部相干散射时的输出性能,与标准MVDR算法、LSMI、RCB、文献[11](Eigenspace-Based)、文献[9]SQP(sequential programming)、文献[10]算法进行比较.其中LSMI算法的加载量取的是噪声功率的两倍,RCB算法的导向矢量误差范数ε=3.
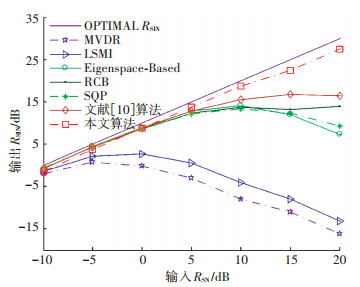
仿真2 2个独立干扰分别位于-40°, 50°方向,本文算法选取投影区间为[-45°, -35°]∪[45°, 55°],信噪比RSN=0 dB.首先考察在出现信号波前扰动失真时,本文算法的波束输出性能.在实际环境中,波通过非均匀介质,独立相位失真增量将在期望信号导向矢量中累积,设定在每次仿真中,期望信号相位的增量服从均值为0、标准差为0.04的高斯分布. 图 3为几种算法在出现波前失真时输出RSIN随输入RSN的变化曲线.
|
图 3 波前扰动失真时的各算法RSIN随RSN变化曲线 Figure 3 Output RSIN of the beamformers versus input RSN in the case of wavefront distortion |
再考察考察在出现局部相干散射时,本文算法的阵列输出性能.存在局部相干散射时,期望信号导向矢量可以表示为[10]
| $ \boldsymbol{a} = {\boldsymbol{a}_0} + \sum\limits_{i = 1}^D {\exp \left( {{\rm{j}}{\varphi _i}} \right)\boldsymbol{a}\left( {{\theta _i}} \right)} . $ |
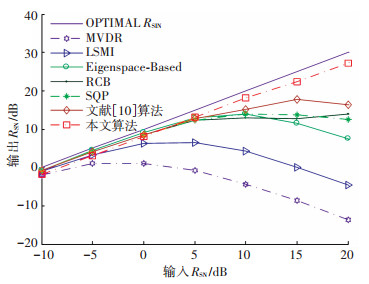
式中:a0是直接路径达到信号的导向矢量;a(θi),i=1, …, D表示从θi方向入射的相干散射信号;φi是直接路径到达信号与相干散射信号的相位差.设定D=4,θi是服从均值为0°、标准差为1°的高斯分布的随机变量,φi服从在[0, 2π]上的均匀分布. 图 4为几种算法在出现局部相干散射时输出RSIN随输入RSN的变化曲线.
|
图 4 局部相干散射时各算法RSIN随RSN变化曲线 Figure 4 Output SINR of beamformers versus input SNR in the case of coherent local scattering |
从图 3和图 4中可以看到:在存在波前扰动失真和局部相干散射时,标准MVDR算法的输出RSIN随输入RSNQ的增大急剧下降;RCB算法有比较好的稳健性,但是在输入RSN较大时,与最优的输出RSIN相差较大;文献[10]算法在RSN < 20 dB时,性能较好,但在信号功率接近干扰功率时,性能下降较快,这是由于文献[10]算法约束条件过于松弛,在干扰功率与期望信号功率接近时,对期望信号与干扰信号的分辨能力下降造成的;本文算法表现出极强的抗波前扰动失真和局部相干散射性能,尤其是输入RSN>10 dB时,其输出RSIN远高于其他算法,在整个输入RSN范围内都有较好的输出RSIN.
3.3 抗期望信号导向矢量DOA估计失配时的性能仿真与分析分别考察本文算法在导向矢量DOA估计出现小角度(3°)和大角度(7°)失配时的阵列输出性能,并将本文算法与文献[15]算法进行比较.
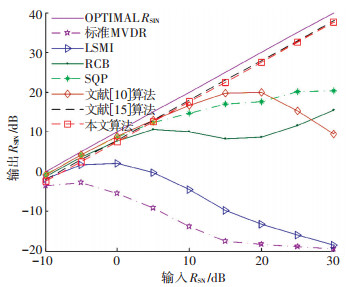
仿真3 2个独立干扰分别位于-40°, 50°方向,期望信号实际从0°方向入射,估计的方向分别设定为3°和7°,即期望信号导向矢量出现了3°和7°的失配量,信噪比RSN=0 dB. 图 5为几种算法在出现3°失配时输出RSIN随输入RSN的变化曲线,图 6为几种算法在出现7°失配时输出RSIN随输入RSN的变化曲线.
|
图 5 导向矢量存在3°失配时各算法RSIN随RSN变化曲线 Figure 5 Output RSIN of beamformers versus input RSN with 3° steering direction error |
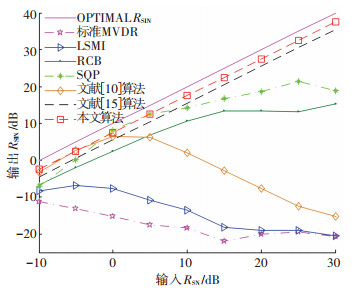
从图 5中可以看出,当期望信号导向矢量出现小角度(3°)失配时,本文算法输出RSIN与文献[15]接近,都优于其他文献算法,但本文算法不再需要干扰的大致来波方向这一先验信息,是一种自适应处理算法.从图 6中可以看出,当期望信号导向矢量出现大角度(7°)时,文献[15]算法性能出现较大下降,本文算法具有最好的输出RSIN,在输入RSN相同时,输出RSIN比文献[15]高出1.8 dB.
|
图 6 导向矢量存在7°失配时各算法RSIN随RSN变化曲线 Figure 6 Output RSIN of beamformers versus input RSN with 7° steering direction error |
考察本文算法在同时出现快速运动干扰和导向矢量DOA估计失配时的阵列输出性能.
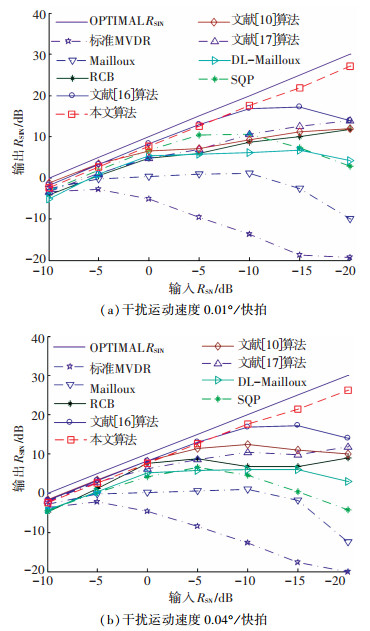
仿真4 考察在同时出现快速运动干扰和导向矢量误差时,本文算法与其他算法的波束输出性能.设定一个干扰信号从-40°向0°方向运动,运动速度分别为0.01°/快拍和0.04°/快拍,期望信号的实际来波方向为0°,由于DOA估计误差,阵列对期望信号的响应方向为3°.本文算法选取投影区间为[-40°, -30°].为了更有比较性,参考文献[17],将Mailloux零陷加宽算法与对角加载相结合(DL-Mailloux),同时与最新的零陷展宽方法文献[16]进行比较. 图 7为几种算法在干扰运动速度分别为0.01°/快拍和0.04°/快拍时的输出RSIN随输入RSN变化曲线.
|
图 7 同时存在运动干扰与导向矢量误差时各算法输出RSIN Figure 7 Output RSIN of beamformers versus input RSN when the jammer motion and steering vector error exist simultaneously |
从图 7中可以看到:同时存在快速运动干扰与导向矢量失配时,DL-Mailloux算法较Mailloux算法性能有较大的提升,这是由于其不但展宽了零陷,抑制了运动干扰,同时引入对角加载技术,具有了一定的抗导向矢量失配能力;文献[16]算法由于能够形成比DL-Mailloux算法更深的零陷,因此算法输出RSIN优于DL-Mailloux算法;文献[17]算法由于同时考虑了协方差矩阵失配与导向矢量失配的问题,因而对快速运动干扰与导向矢量失配都具有较好的稳健性,输出性能较RCB算法好;本文算法的输出性能优于文献[17]算法和文献[16]算法,表现出极强稳健性,这是由于本文算法不但展宽了零陷,而且加深了零陷深度,更地的抑制快速运动干扰,同时具有较强的抗导向矢量失配能力,在整个输入RSN范围内都有很好地输出RSIN,波束输出性能远远优于其他算法.
4 结语本文提出的抗导向矢量失配的零陷展宽自适应波束形成方法通过零陷展宽投影变换技术扩张干扰入射方向,展宽零陷宽度,加深零陷深度,能够很好地抑制快速运动强干扰,同时通过主瓣区域幅度响应约束技术,增强波束形成器对波前扰动失真、局部相干散射等系统误差引起的期望信号导向矢量失配的稳健性.该方法在同时出现快速运动干扰和导向矢量失配时,也能稳定工作,具有很好的波束保形能力和较高的输出RSIN,相比目前多数稳健波束形成算法有更好的干扰抑制效果和更高的输出RSIN.
| [1] | VAN TREESH L. Optimum array processing[M]. New York: Wiley, 2002 : 710 -887. |
| [2] | LI Hongtao, WANG Ke, WANG Chaoyu, et al. Robust adaptive beamforming based on worst-case and norm constraint[J]. International Journal of Antennas and Propagation,2015, 2015 (1) : 1-7. DOI: 10.1155/2015/765385 |
| [3] | HUANG Lei, ZHANG Jing, XU Xu, et al. Robust adaptive beamformingwith a novel interference-plus-noise covariance matrix reconstruction method[J]. IEEE Transactions on Signal Processing,2015, 63 (7) : 1643-1650. DOI: 10.1109/TSP.2015.2396002 |
| [4] | VOROBYOV SA. Principles of minimum variance robust adaptive beamforming design[J]. Signal Processing,2013, 93 (12) : 3264-3277. DOI: 10.1016/j.sigpro.2012.10.021 |
| [5] | LI Wenxing, MAO Xiaojun, YU Wehua, et al. Robust adaptive array beamforming based on modified norm constraint algorithm[J]. Applied Computational Electromagnetics Society Journal,2014, 29 (12) : 1060-1066. |
| [6] | SONG H, KUPERMAN W A, HODGKISS W S, et al. Null broadening with snapshot-deficient covariance matrices in passive sonar[J]. IEEE Journal of Oceanic Engineering,2003, 28 (2) : 250-261. DOI: 10.1109/JOE.2003.814055 |
| [7] | COX H, ZESKIND R M, OWEN M H. Robust adaptive beamforming[J]. IEEE Transactions on Acoustics Speech and Signal Processing,1987, 35 (10) : 1365-1376. DOI: 10.1109/TASSP.1987.1165054 |
| [8] | LI Jian, STOICA P, WANG Zhisong. On robust capon beamforming and diagonal loading[J]. IEEE Transactions on Signal Processing,2003, 57 (7) : 1702-1715. DOI: 10.1109/TSP.2003.812831 |
| [9] | HASSANIEN A, VOROBYOV S A, WONG K M. Robust adaptive beamforming using sequential programming: An iterative solution to the mismatch problem[J]. IEEE Signal Processing. Letters,2008, 15 : 733-736. DOI: 10.1109/LSP.2008.2001115 |
| [10] | KHABBAZIBASMENJ A, VOROBYOV S A, HASSANIEN A. Robust adaptive beamforming based on steering vector estimation with as little as possible prior information[J]. IEEE Transactions on Signal Processing,2012, 60 (6) : 2974-2987. DOI: 10.1109/TSP.2012.2189389 |
| [11] | CHANG L, YEH CC. Performance of DMI and eigenspace-based beamformers[J]. IEEE Transactions on Antennas and Propagation,1992, 40 (11) : 1336-1347. DOI: 10.1109/8.202711 |
| [12] |
范展, 梁国龙, 王逸林. 一种零陷展宽鲁棒自适应波束形成算法[J].
电子与信息学报,2013, 35 (11) : 2764-2770.
FAN Zhan, LIANG Guolong, WANG Yilin. Robust Adaptive Beamforming with Null Widening[J]. Journal of Electronics & Information Technology,2013, 35 (11) : 2764-2770. DOI: 10.3724/SP.J.1146.2013.00087 |
| [13] | MAILLOUX R J. Covariance matrix augmentation to produce adaptive array pattern roughs[J]. Electronics Letters,1995, 31 (10) : 771-772. DOI: 10.1049/el:19950537 |
| [14] | ZATMAN M. Production of adaptive array troughs by dispersion synthesis[J]. Electronics Letters,1995, 31 (25) : 2141-2142. DOI: 10.1049/el:19951486 |
| [15] |
李文兴, 毛晓军, 孙亚秀. 一种新的波束形成零陷展宽算法[J].
电子与信息学报,2014, 36 (12) : 2882-2888.
LI Wenxing, MAO Xiaojun, SUN Yaxiu. A new algorithm for null broadening beamforming[J]. Journal of Electronics & Information Technology,2014, 36 (12) : 2882-2888. DOI: 10.3724/SP.J.1146.2013.02018 |
| [16] | AMAR A, DORON M A. A linearly constrained minimum variance beamformer with a pre-specified suppression level over a pre-defined broad null sector[J]. Signal Processing,2015, 109 (1) : 165-171. DOI: 10.1016/j.sigpro.2014.11.009 |
| [17] | VOROBYOV S A, GERSHMAN A B, LUO Zhiquan, et al. Adaptive beamforming with joint robustness against mismatched signal steering vector and interference nonstationarity[J]. IEEE Signal Process Letters,2004, 11 : 108-111. DOI: 10.1109/LSP.2003.819857 |
| [18] | GUERCI J R. Theory and application of covariance matrix tapers for robust adaptive beamforming[J]. IEEE Transactions on Signal Processing,1999, 47 (4) : 977-985. DOI: 10.1109/78.752596 |
| [19] | YU Zhuliang, GU Zhenghui, ZHOU Jianjiang, et al. A robust adaptive beamformer based on worst-case semi-definite programming[J]. IEEE Transactions on Signal Processing,2010, 58 (11) : 5914-5919. DOI: 10.1109/TSP.2010.2058107 |
| [20] | LUO Zhiquan, MA Wingkin, SO A M C, et al. Semidefinite relaxation of quadratic optimization problems[J]. IEEE Signal Processing Magazine,2010, 27 (3) : 20-34. DOI: 10.1109/MSP.2010.936019 |
| [21] | GRANT M, BOYD S, YE Y Y. CVX: Matlab Software for Disciplined Convex Programming. Jun. 2014 [Online]. Available: http://cvxr.com/cvx/. |
| [22] | STOICA P, MOSES R L. Introduction to Spectral Analysis[M]. Upper Saddle River, NJ: PrenticeHall, 1997 : 221 -247. |
 2016, Vol. 48
2016, Vol. 48


