热轧带钢轧后冷却板形控制的关键是进行均匀化的冷却,使得层流冷却结束后沿宽度方向温度分布均匀.在常规层流冷却过程中,引起宽度方向不均匀冷却的因素有很多.一般在精轧机出口处的边部温度较低,水冷过程中带钢上表面的滞留冷却水层从边部流出,下表面冷却水回落到钢板的两边,造成带钢边部的水量急剧增加,加重了边部的温度过冷.这种边部过冷会造成沿宽度方向上的组织和应力分布不均,严重的还会引起边浪的板形缺陷,引起水冷过程中的次生不均匀冷却,恶化钢板的质量[1-2].
板形控制要以整个冷却过程中的板形良好为准,目前有许多关于热轧带钢层流冷却过程中的边部遮蔽研究. Sun[3]和Wang[4]等人采用等宽度边部遮蔽的方式,研究了遮蔽不同宽度时的横向温度、残余应力的不同,得出相对合理的遮蔽宽度,但是卷取时带钢的温度和残余应力分布并不均匀,板形仍未达到理想的平直状态,且没有考虑相变的影响和水冷过程中应力的变化. Jae Kon[5]等人的研究中,分别考虑边部遮蔽对晶粒大小、组织分布和残余应力的影响,发现在边部遮蔽处由于冷速减慢,晶粒会变得粗大,不同钢种边部遮蔽同样的宽度,得到的效果不同. S. Peregrina[6]等人研究了实际生产过程中等宽边部遮蔽工艺和常规层流冷却工艺的差别,证明边部遮蔽的方式能有效改善带钢横向和纵向上的温度均匀性.
带钢实际生产过程中,横向温度的均匀性控制主要是通过调节上部集管的水量分布,形成中凸形的水流分布形式,或采用通过在冷却装置上采用边部遮蔽的方式,根据不同的带钢宽度、厚度采用等宽边部遮蔽的方式,来减小横向上的温度分布不均现象[7-8].若遮蔽宽度不当,会导致水冷过程中带钢边部局部范围内的断流现象,造成边部冷却能力不足,引起宽度方向残余应力分布不均和材料力学性能的下降.为了解决水冷过程中的板形不良现象,本文采用了离散化边部遮蔽的策略,对不同的集管遮蔽不同的宽度,优化出合适的遮蔽策略,改善12 mm厚度的X70管线钢层流冷却过程中横向温度、组织、应力分布的均匀性.
1 有限元模型的建立 1.1 几何模型选取6 m长的X70管线钢建立层流冷却的三维模型,取宽度方向上的1/2为几何模型,尺寸为6 000 mm×775 mm ×12 mm,网格数为20×20×10,并对边部和上下表面的单元进行细化,单元类型为精度较高的八节点六面体单元,如图 1所示.

|
图 1 有限元几何模型 Figure 1 Finite element model |
层流冷却过程的初始条件为终轧后的温度,不考虑温度沿带钢长度、厚度方向上的变化和初始应力分布,终轧温度目标值为790 ℃,在精轧出口用红外线测温仪对带钢温度分布进行检测,并对测量的数据进行简化,得到带钢沿宽度方向上初始温度分布如图 2所示,在长度和厚度方向上假设温度分布均匀[9].

|
图 2 Finite element model Figure 2 Initial temperature distribution in width direction |
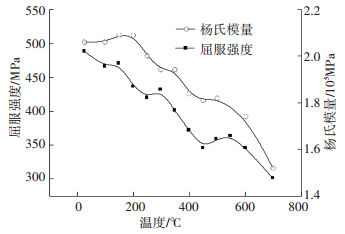
材料的物性参数包括比热容、热传导系数使用相关文献数据[10],假设材料是各向同性的,X70管线钢的密度为7841 Kg·m-3,化学成分如表 1所示. X70钢的热膨胀系数、弹性模量、屈服强度都是随温度变化的变量,在Formaster-Digital型热膨胀仪测定X70钢在15 ℃·s-1连续冷却条件下线膨胀系数的变化,对实验数据进行处理,结果如图 3所示,杨氏模量和屈服强度如图 4所示[9].
| 表 1 X70钢的化学成分 Table 1 Chemical composition of X70 steel |

|
图 3 X70钢热膨胀系数 Figure 3 Coefficient of thermal expansion of X70 steel |
|
图 4 X70钢屈服强度和杨氏模量 Figure 4 Yield strength and Young's modulus of X70 steel |
层流冷却中的边界条件主要包括换热系数和位移边界的确定.冷却时带钢的传热过程主要包括空冷及水冷部分,空冷时总热交换系数可表示为
| $ \begin{array}{c} {h_j} = {h_r} + {h_d},\\ {h_d} = 2.15{\left( {{T_s} - {T_\infty }} \right)^{0.25}},\\ {h_r} = \varepsilon {\sigma _0}\left( {T_s^2 + T_\infty ^2} \right)\left( {{T_s} - {T_\infty }} \right). \end{array} $ | (1) |
式中:hj为空冷时总的换热系数,W·m-2·K-1;hr为热辐射换热系数,W·m-2·K-1;hd为热对流换热系数,W·m-2·K-1;σ0为Stefan-Boltzman常数,W·m-2·K-4;ε为辐射率;Ts为带钢表面温度,K;T∞为环境温度,K.
式(1)中的热辐射率ε与钢板的表面温度有关.随着钢板表面温度的变化,辐射率也会产生变化,具体的变化情况可由下式得出:
| $ \varepsilon = 1.1 + \frac{{{T_s}}}{{1\;000}}\left( {0.125\frac{{{T_s}}}{{1\;000}} - 0.38} \right). $ |
水冷区换热系数的经验公式为
| $ \begin{array}{l} H_w^c = \frac{{9.72 \times {{10}^5}{\omega ^{0.355}}}}{{{T_s} - {T_w}}} \cdot \\ \;\;\;\;\;\;\;{\left\{ {\frac{{\left( {2.5 - 1.5{{{\mathop{\rm logT}\nolimits} }_w}} \right)D}}{{{p_i}{p_c}}}} \right\}^{0.645}} \times 1.163. \end{array} $ |
考虑到宽度方向上边部的冷却能力大于中部,使用下式来描述Hw的值:
| $ {H_w} = \left\{ \begin{array}{l} H_w^c\left( {1 + 0.25\frac{{10x - 4B}}{B}} \right),ifx > 0.4B;\\ H_w^c,ifx \le 0.4B. \end{array} \right. $ |
式中:B为带钢的宽度,m;Hw、Hwc分别为带钢板表面和带钢中部的层流冷却水冷换热系数,W· m-2· k-1;ω为水流密度,m3·min-1·m-2;Ts、Tw分别为带钢表面温度和水温,K;D为上、下喷嘴直径,m;pi、pc别为轧线方向和轧线垂直方向的上、下集管喷嘴间距,m.
采用离散化的边部遮蔽策略,使带钢边部范围内达到温度冷却相对均匀的目的,采取的遮蔽策略组合为:共开启9组集管,每组有4支冷却集管,每只集管有2排喷水U型管,对每组集管边部遮蔽的宽度分别为120、0、80、0、60、0、30、0、10 mm,即间隔不均匀遮蔽的方式,如图 5所示,黑色部分为边部遮蔽区域.假设钢板未遮蔽处为常规层流冷却的换热系数,被遮蔽处的换热系数hfb按照稳定膜沸腾区换热系数处理,稳定膜沸腾区换热系数公式为[11]
| $ \begin{array}{l} {h_{fb}} = {\lambda _s}{\left( {\frac{{g\Delta \rho }}{{8\pi {\lambda _s}{\alpha _c}}}} \right)^{1/3}},\\ \;\;\;\;\;{\alpha _c} = \frac{{{\lambda _s}{\theta _s}}}{{2{i_{fc}}{\rho _S}}}. \end{array} $ |

|
图 5 离散化边部遮蔽的组合策略 Figure 5 Illustration of a combination strategy for the discretization of edge masking |
式中:hfb为稳态稳定膜沸腾区的换热系数,W· m-2· k-1;Δρ为密度差,Kg·m-3,Δρ=ρ1-ρs;λs为饱和蒸汽下的导热系数,W· m-1· k-1;θs为饱和蒸汽下的温度差,K,θs=T-T1;ifc为单位蒸发比焓,J·kg-1.
位移边界条件根据工厂实际条件建立,对于在线冷却的整长带钢,可以认为长度方向是无限的,因此当取三维平板分析时,带钢两个端部上每个节点沿长度方向的位移量是一致的[12].假定带钢静止,边界条件随带钢移动,故位移边界条件设定为:1) 带钢的两端为长度方向耦合约束Uz=0;2) 由于对称关系取带钢的一半进行分析,带钢中部一端Ux=0, Uy=0, Uy=0,其中Ux,Uy,Uz为三个方向的位移.
1.5 相变模型相变计算是以相变理论及Scheil叠加法则为基础,根据Avrami方程建立奥氏体向铁素体、贝氏体连续冷却相变数学模型,通常假设新相形核发生在奥氏体晶界,奥氏体的等温分解动力学可用Avrami型方程表达:[13]
| $ X = 1 - \exp \left( { - k{t^n}} \right). $ | (2) |
式中参数k和n的值,可以通过等温转变曲线(TTT)中对应某一温度T的两个等温时间ts、te及其转变量Vs、Ve求得:
| $ \begin{array}{l} n = \frac{{\ln \left[ {\frac{{\ln \left( {1 - {V_s}} \right)}}{{\ln \left( {1 - {V_e}} \right)}}} \right]}}{{\ln \left( {\frac{{{t_s}}}{{{t_e}}}} \right)}},\\ k = - \frac{{\ln \left( {1 - {V_s}} \right)}}{{t_s^n}}. \end{array} $ |
由于转变量与时间的关系随温度而变化,因此k、n也随温度而不同.对于铁素体、珠光体和贝氏体转变,因为k、n随冷速和温度而变,所以只有从实际转变开始时间计算,才能使计算结果与实际情况相符,因此式(2)中的t应由t-ts替换,ts为相变孕育期.得出新的扩散型相变量的表达式为
| $ X = 1 - \exp \left[ { - k{{\left( {t - {t_s}} \right)}^n}} \right]. $ |
式中参数k是与温度(过冷度)相关的函数,时间t表示相变开始后的时间,而相变的开始时间ts可以通过Scheil法则确定,即相变孕育期符合可加性原则.
1.6 应力应变模型应力应变模型包括弹塑性变形和热膨胀应变.至于层流冷却期间发生的相变膨胀应变和相变诱导塑性应变已经包含在试验测得的热膨胀应变之中,不再进行考虑,故总应变可以用如下方程表示:
| $ {{\dot \varepsilon }^t} = {{\dot \varepsilon }^e} + {{\dot \varepsilon }^{{\rm{th}}}} + {{\dot \varepsilon }^p}. $ |
式中:
X70钢层流冷却过程中会发生相变并产生相变潜热,相变潜热qv是相变速率的函数,相变潜热的计算公式为
| $ {q_v} = \Delta H\frac{{{f_{n + 1}} - {f_n}}}{{\Delta t}} = \Delta H\Delta f. $ |
式中:ΔH为奥氏体分解时的相变焓,Δf为单位时间的相变程度.奥氏体分解时的热焓值ΔH如表 2所示[14].
| 表 2 奥氏体分解时的热焓值 Table 2 Thermal enthalpy of austenite decomposition |
Marc提供了大量的子程序接口,用Fortran语言编程加载自定义边界条件,分别用子程序Ufilm确定随温度变化的对流换热系数;子程序Ubginc加载相变动力学模型,定义相变组织、相变增量、相变孕育时间等;子程序Flux计算相变生成热;子程序Plotv输出贝氏体和铁素体的生成量.采用热力耦合的计算方法,直接进行温度、相变和应力三者之间的耦合计算.
2 计算结果及分析 2.1 温度场和组织转变计算结果分析采用某2160 mm热轧带钢厂层流冷却工艺参数进行模拟,X70管线钢冷却方式为前端冷却,出精轧口之后经历6.55 s的空冷,然后是18.65 s的水冷,水冷结束之后为34.29 s的空冷.
图 6分别为采用两种冷却工艺后,卷取时带钢温度沿宽度方向的计算值和实测值.从图 6可以看出,在带钢中部范围内卷取温度实测值和计算值差值在5 ℃范围内,计算值和实测值吻合较好.采用常规层流冷却工艺后,卷取时带钢中部和边部的温差计算值达到了62 ℃,相比而言,采用离散化边部遮蔽的冷却策略之后,边部150 mm范围内温度更加均匀,中部和边部的温差减小到10 ℃.从计算结果来看,离散化边部遮蔽的冷却工艺能显著改善带钢宽度方向的温度均匀性.

|
图 6 卷取时带钢宽度方向的温度分布 Figure 6 Temperature distribution of strip width direction during coiling |
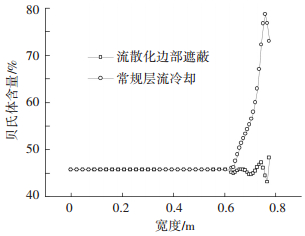
在层流冷却过程中只会发生贝氏体相变,图 7为采用两种冷却工艺后,卷取时沿带钢宽度方向上表面贝氏体转变量的分布规律.从图 7可以看出:常规层冷后带钢中部的贝氏体转变量为45.7%,边部150 mm范围内贝氏体转变量逐渐增加,最大达到了78.6%,边部和中部的贝氏体转变量在带钢宽度方向上的分布严重不均匀;采用改进后的冷却工艺后,带钢边部的贝氏体转变量计算值和中部差值在3.2%范围之内,带钢宽度方向上组织分布更加均匀.
|
图 7 卷取时带钢宽度方向的贝氏体含量分布 Figure 7 Distribution of bainite in strip width direction during coiling |
图 8为在两种冷却工艺条件下,带钢上表面中部和距离边部9、30 mm处的温度、贝氏体转变量差值绝对值随时间的变化规律.从图 8(a)可以看出:与常规层流冷却的工艺相比,采用离散化边部遮蔽的冷却工艺之后,在层冷过程中中部和距离边部9 mm处的温差最大值由160.4 ℃减小到54.1 ℃,边部和中部的贝氏体转变量之差的最大值则由31.5%减小到4.9%;同时中部和距离边部30 mm处的温差范围由46.8 ℃减小到了15.2 ℃,贝氏体转变量差值范围由27.3%减小到了2.37%.可见在采用离散化边部遮蔽的冷却工艺后,在层流冷却过程中带钢边部的温降显著变小,宽度方向上的贝氏体转变量趋于均匀,利于降低带钢宽度方向上的热应力和组织应力差异,从而使冷却过程中的应力分布均匀;宽度方向上温差的减小也有利于减小冷却过程中中部和边部的平均冷却速度差,从而使带钢宽度方向上的晶粒尺寸大小均匀,力学性能良好.

|
图 8 带钢上表面中部和边部的温差和贝氏体转变量差值 Figure 8 Temperature and bainite transformation difference between middle and edge of upper surface of the strip |
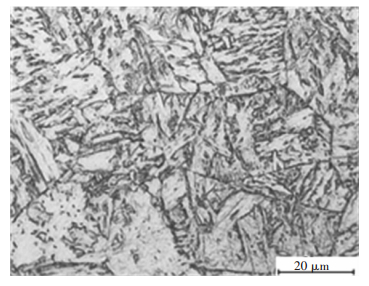
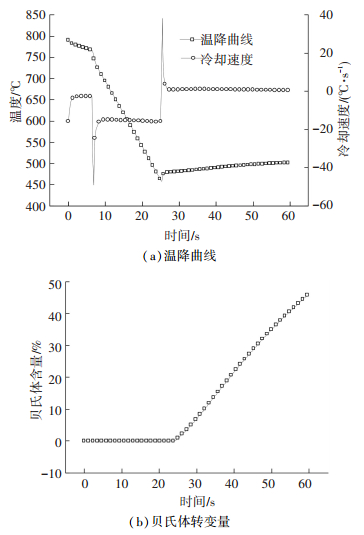
相变场可以根据在连续冷却下的X70钢组织、相变点温度来验证.取工业X70钢钢坯,切成φ4×10的小圆柱,采用Formaster-Digital热膨胀仪和Gleeble 3500热模拟机测定X70钢的相变点和不同冷却速率下的热膨胀曲线.根据不同冷却速度下的温度-膨胀量曲线,找出不同冷速下的相变起始点温度和终止点温度.工艺路线为以10.5 ℃·s-1的速度加热至1 050 ℃保温3 min,然后以5 ℃·s-1的速度冷至950 ℃保温10 s,之后以不同的速度冷却至室温.在15 ℃·s-1的冷却速率下,得到X70钢金相组织如图 9所示,为针状铁素体,在铁素体内部和晶界处存在点状或条状的M-A岛.从X70钢层流冷却过程中钢板中部上表面的温降曲线和贝氏体转变计算结果来看,贝氏体转变开始时间为冷却开始后的24 s,此时带钢温度为476 ℃,冷却速度为16.1 ℃·s-1,如图 10所示.贝氏体转变的开始和结束温度的计算值和实测值的对比如表 3所示,在15 ℃·s-1冷却速度下贝氏体开始转变温度为458 ℃,计算值和实测值的相对误差为18 ℃,转变结束温度相对误差为1 ℃.因此,所建立的相变动力学模型具有相当高的精确性.
|
图 9 X70钢15 ℃·s-1在的冷速下的微观组织 Figure 9 Microstructure of X70 steel at cooling rate of 15 ℃·s-1 |
|
图 10 X70钢冷却过程温度和贝氏体转变量随时间的变化 Figure 10 Change of cooling process temperature and bainite transformation in X70 steel |
| 表 3 15 ℃·s-1的冷速下贝氏体转变开始和结束温度 Table 3 Starting and end temperature of bainite transformation at cooling rate of 15 ℃·s-1 |
X70钢层流冷却过程中,从精轧机出口的790 ℃冷却到卷取时的500 ℃,期间经历贝氏体相变.从图 3可以看出,在450 ℃至600 ℃之间,带钢的热膨胀系数在会发生急剧的变化,水冷过程中横向的温度分布不均所引起的应力分布形式会更加多样化,同时相变潜热所释放的热量也会影响带钢内应力的大小.
12 mm厚度的X70钢的轧向应力的确定应该以厚度方向上平均值为准,而不应片面地取某一个面上的应力. 图 11为层流冷却过程中,带钢轧向应力在不同时间下的分布规律.从图 11(a)可以看出:在常规层流冷却过程中,在8.12 s和12.3 s时,带钢边部20 mm范围内出现了应力不均的现象,对板形影响较小;随着冷却的进行,带钢边部的温降增大,边部的压应力开始增大,在18.8 s时达到了最大值-538.2 MPa,并且应力不均范围扩大到了150 mm的宽度,带钢板形有向边浪发展的趋势;之后边部发生贝氏体相变,相变产生的组织应力和热应力的方向相反,带钢边部的压应力开始减小,在水冷结束的25.2 s时,带钢边部80 mm范围内为不均匀分布的拉应力,最大达到了320 MPa,带钢板形有向中浪发展的趋势;在随后的空冷过程中,由于带钢内部热传导和相变潜热的综合作用,中部和边部的温降逐渐减小,卷取时横向上的应力分布基本均匀.因为钢卷在卷取冷却过程中仍然会发生应力及板形变化,室温下的测量应力无法反映层流冷却后的应力实际值,层流冷却过程中因速度和温度原因,也无法直接测量带钢的应力和应变,根据生产过程观察,在层流冷却中X70管线钢在冷却过程中存在横向U型弯曲,同时伴有边浪,上述现象与应力计算的结果一致.采用离散化边部遮蔽的层流冷却工艺之后,由于减小了冷却过程中边部和中部的温度差、组织转变差,从图 11(b)的计算结果来看,冷却过程中带钢横向上的轧向应力分布相对均匀,分布范围在-125.8~116 MPa,能有效减小边部的内应力大小,改善水冷过程中的板形不良现象,防止钢板发生次生的不均匀冷却.

|
图 11 层流冷却过程中带钢宽度方向的轧向应力分布 Figure 11 Stress distribution in strip width direction during the laminar cooling process |
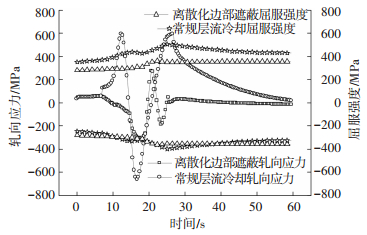
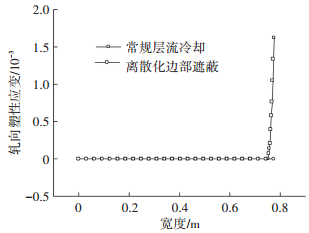
图 12为带钢边部上表面轧向应力和屈服强度随时间的变化规律.从图 12可以看出:在采用改进后的冷却工艺之后,整个冷却过程中的内应力都没未超过带钢边部在对应温度处的屈服强度.在常规层流冷却过程中当水冷至11 s时,拉应力计算值为379.5 MPa,超过了该温度下带钢的屈服强度330.5 MPa;当冷却至15.3 s时,边部的压应力计算值会再次超过带钢的屈服强度;水冷结束时,边部的拉应力达到了569.7 MPa,也超过了带钢在此温度下的屈服强度424 MPa,因此在冷却过程中带钢边部会存在塑性应变.卷取时带钢横向上的轧向塑性应变规律如图 13所示.从图 13可以看出:在常规层流冷却过程中,带钢横向上边部25 mm范围内的内应力会超过带钢的屈服应力,产生塑性变形,最大达到了1.62×10-3;相对而言,在采用离散化边部遮蔽的层流冷却工艺之后,从计算结果来看,卷取时在带钢横向上没有产生轧向塑性应变,有效的消除了残余塑性应变对之后钢卷冷却的不良影响,有利于获得室温时的良好板形.
|
图 12 带钢边部上表面应力与屈服强度变化 Figure 12 Surface stress and yield strength change at the edge of strip |
|
图 13 层流冷却结束后带钢长度和宽度方向塑性应变分布 Figure 13 Plastic strain distribution in strip length and width direction at the end of laminar cooling |
热轧带钢层流冷却过程中板形缺陷问题的研究历来存在很多分歧. Zhou等[15]认为水冷结束后边部会产生拉应力,带钢板形向中浪发展,YOSHIDA H等[16-18]认为在层流冷却过程中,带钢边部会产生压应力,板形会向边浪发展.这是因为他们研究钢种有一定区别,冷却工艺也不尽相同,由于不同刚种的成分和相变区间不同,热膨胀系数大小和随温度的变化趋势是不一样的,边部温降所引起的应力大小也就更加多样化.可以肯定的是,层流冷却过程中板形缺陷的根本原因是横向温度分布不均匀,从本文模拟的结果来看,离散化的边部遮蔽冷却策略能有效改善带钢卷取前的板形不良现象.但是对于X70管线钢而言,在卷取过程中和卷取之后的钢卷冷却过程中,仍然会发生相变并产生残余应力,影响开卷之后的室温板形,这些问题仍需进一步研究.
3 结论1) 建立了热轧带钢层流冷却过程中的有限元模型,对微观组织和温度的计算值和实测值进行了对比分析,表明计算值和实测值吻合较好,模型具有较高的精确性.在常规层流冷却过程中,卷取时12 mm厚度X70钢中部和边部的温差达到了62 ℃,边部最大贝氏体转变量达到了78.6%,中部仅为45.7%;采用离散化边部遮蔽的冷却工艺,卷取时中部和边部的温度差减小至10 ℃,贝氏体转变量差值在3.2%范围之内,而且带钢在冷却过程中的横向温度、贝氏体分布均匀性得到了有效改善.
2) 常规层流冷却过程中,带钢宽度方向的轧向应力分布严重不均匀,在水冷的后半段,前期边部150 mm范围内会出现不均匀的压应力,最大值达到了-538.2 MPa,板形有向边浪发展的趋势,随后边部的压应力会逐渐转变为拉应力,板形有向中浪发展的趋势;改进后的冷却工艺能显著减小边部的应力,冷却过程中横向应力的波动在-125.8~116 MPa之间,可有效改善轧向应力的横向分布均匀性.
3) 常规层流冷却过程中,带钢边部25 mm范围内发生了塑性变形,最大应变1.62×10-3,而采用离散化边部遮蔽的冷却策略后,卷取时边部的塑性变形得到有效的消除,有利于获得良好的板形.
| [1] |
王峰丽, 李红芳, 李谋渭. 中厚板淬火过程的横向冷却曲线[J].
钢铁研究学报,2002, 14 (3) : 39-42.
WANG Fengli, LI Hongfang, LI Mouwei. Transverse cooling curve in quenching medium steel plate[J]. Journal of Iron and Steel Research,2002, 14 (3) : 39-42. |
| [2] |
崔乃忠. 基于ANSYS平台的中厚板控冷过程的横向冷却曲线[J].
钢铁技术,2004, 12 (5) : 13-15.
CUI Naizhong. Transverse cooling curve of medium steel plate in the process of controlled cooling based on ANSYS platform[J]. Iron and Steel Technology,2004, 12 (5) : 13-15. |
| [3] | SUN W, SHAO J, HE A, et al. Research on residual stress quantitative reduction in laminar Cooling on hot strip mill[J]. International Journal of Heat and Technology,2015, 33 (4) : 19-23. DOI: 10.18280/ijht |
| [4] | WANG D A, LO W, HWUB Y J, et al. Finite element analyses of TMCP steel plates with consideration of edge masking[J]. Procedia Engineering,2013 (1) : 762-767. |
| [5] | LEE J K, KAN K B, LEE K J, et al. Modelling of the microstructure and the mechanical property variation across the transverse direction of hot rolled steels and the effect of edge shielding[J]. ISIJ International,1998, 38 (7) : 752-758. DOI: 10.2355/isijinternational.38.752 |
| [6] | S.PEREGRINA S, J-M. GARCÍA REDONDO J M. Hot strip flatness optimization by means of edge masking in the ROT[J]. La Revue de Métallurgie-CIT,2006, 103 (9) : 381-387. DOI: 10.1051/metal:2006147 |
| [7] |
杜平. 基于MULPIC装置的宽厚板均匀冷却控制[J].
轧钢,2012, 29 (6) : 7-10.
DU Ping. Application and research of wide thick plate homogeneous cooling based on MULPIC device[J]. Steel Rolling,2012, 29 (6) : 7-10. |
| [8] |
陈银莉, 余伟, 白冰. 低残余应力热轧带钢层流冷却工艺的数值模拟[J].
北京工业大学学报,2012, 38 (10) : 1576-1581.
CHEN Yinli, YU Wei, BAI Bing. Numerical simulation of laminar cooling process for hot rolled strip with low residual stress[J]. Journal of Beijing University of Technology,2012, 38 (10) : 1576-1581. |
| [9] |
余伟, 卢小节, 陈银莉, 等. 卷取温度对热轧X70管线钢层流冷却过程残余应力的影响[J].
北京科技大学学报,2011, 33 (6) : 722-728.
YU Wei, LU Xiaojie, CHEN Yinli, et al. Effect of coiling temperature on residual stresses in hot rolled X70 pipeline steel strips during laminar cooling[J]. Journal of University of Science and Technology Beijing,2011, 33 (6) : 722-728. |
| [10] |
卢小节.热轧管线钢轧后快冷中温度场、相变和应力场的研究[D].北京:北京科技大学, 2010: 10.
LU Xiaojie. Study on temperature field, transformation and stress of pipeline steel during the fast cooling process after rolling[D].Beijing: University of Science and Technolgy, 2010:10. |
| [11] | PRIETO M M, RUIZ L S, MENENDEZ J A. Thermal performance of numerical model of hot strip mill runout table[J]. Ironmaking and Steelmaking,2001, 28 (6) : 474-480. DOI: 10.1179/irs.2001.28.6.474 |
| [12] |
张清东, 戴杰涛. 带钢板形翘曲变形行为的仿真[J].
北京科技大学学报,2011, 33 (8) : 1006-1012.
ZHANG Qingdong, DAI Jietao. Simulation of warping deformation in thin steel strips[J]. Journal of University of Science and Technology Beijing,2011, 33 (8) : 1006-1012. |
| [13] | KUBAN M B, JAYARAMAN R, HAWBOLT E B, et al. An assessment of the additivity principle in predicting continuous-cooling austenite-to-pearlite transformation kinetics using isothermal transformation data[J]. Metallurgical Transactions A,1986, 17 (9) : 1493-1503. DOI: 10.1007/BF02650085 |
| [14] | WANG K F, HANDRASEKAR C S C, Y YANG H T. Experimental and computational study of the quenching of carbon steel[J]. Journal of Manufacturing Science and Engineering,1997, 119 (3) : 257-265. DOI: 10.1115/1.2831102 |
| [15] | ZHOU Z Q, THOMSON P F, LAM Y, et al. Numerical analysis of residual stress in hot-rolled steel strip on the run-out table[J]. Journal of Materials Processing Technology,2003, 132 (1/2/3) : 184-197. |
| [16] | YOSHIDA H. Analysis of flatness of hot rolled steel strip after cooling[J]. Transactions ISIJ,1984, 24 (3) : 212-220. DOI: 10.2355/isijinternational1966.24.212 |
| [17] |
蔡正.热轧带钢冷却后的屈曲行为研究[D].沈阳:东北大学, 1999.
CAI Zheng. Warping behavior of hot rolled steel strip after cooling[D]. Shenyang: Northeast University, 1999. |
| [18] | WANG X, LI F, YANG Q. FEM analysis for residual stress prediction in hot rolled steel strip during the run out table cooling[J]. Applied Mathematical Modelling,2013 (37) : 586-609. |
 2016, Vol. 48
2016, Vol. 48


