2. 中国地震局 地震工程与工程振动重点实验室,哈尔滨 150080
2. Key Laboratory of Earthquake Engineering and Engineering Vibration, China Earthquake Administration, Harbin 150080, China
基于可靠度的设计理念已逐渐成为工程结构抗震设计和工程安全设计的主流思想.岩土材料是自然历史的产物,而目前岩土参数基本采用试验方法得到.土性参数的不确定性主要来自于两方面:一是内在因素,即土本身固有变异性的影响;二是外在因素的影响,如试验技术、分析方法等.对于土体静力学指标,土性参数的不确定性已经有一些研究成果[1-3].
在土动力学研究中,土体作为地震波传播的介质,其动力性能直接影响结构的安全,其动力参数的估计也直接影响工程造价[4].其中,土的动剪模量和阻尼比是土动力特性两个首要参数,是地震小区划、重大工程抗震设计和地震安全性评价工作中必不可少的分析参数[5-9].共振柱仪原理可靠,分析方法相对简单,是获取土动剪模量比和阻尼比较为理想的仪器,也是国家标准《工程场地地震安全性评价》(GB17741-2005)[10]中规定使用的设备.对任何一个可以重复测量的科学数据,其误差水平、置信区间都是必须回答的问题,但迄今为止共振柱试验误差的研究成果尚少.祝龙根等[11]采用统一的标准砂为样本,对不同类型共振柱仪器得到的试验数据进行了对比研究,结果表明,不同类型共振柱仪试验得到的剪切模量值有一定的离散性.除了不同类型共振柱仪外,单一类型的共振柱试验也会存在试验误差,但目前这方面的研究尚无成果发表.就土的动剪模量比和阻尼比对设计地震动影响问题,已经有一些研究成果[12-14],结果表明动剪切模量比对地震动计算结果来说是一个比剪切波速还要敏感的参数,特别是对位于强震区的三、四类场地,其变异性影响十分显著.但是,由于动剪模量比和阻尼比测试误差尚不得知,以往其对地震动影响研究只能采用假定参数离散程度方式,使分析结果缺乏依据,反之也无法从对地震动影响角度评价现有共振柱试验精度和技术水平,导致对动剪模量比和阻尼比试验精度存在争议.
本文采用单台共振柱仪,设计两种具有代表性的试验组,研究砂土动剪切模量比和阻尼比试验误差问题,讨论测试误差分布形态和基本规律,给出概率统计指标,分析不同类型组之间、模量比和阻尼比之间试验离散性的差异和联系以及试验误差对地震动计算的影响等,为解掌握现有共振柱试验水平以及改进共振柱试验技术提供依据.
1 试验设计 1.1 仪器及样本试验采用中国地震局工程力学研究所研制的我国第一台具有自主知识产权GZ-1改进型仪器,该仪器为固定-自由端型,其可靠性已经得到检验.试验采用自振方式,比较共振试验,这种方式更适于地震荷载作用下土的动力学性能测试.试验所用土样尺寸为Φ39.1 mm×80 mm,所有土样的固结压力均采用100 kPa.重塑砂采用标准砂,其基本物性指标见表 1.
| 表 1 重塑砂基本物性指标 Table 1 Physical indicators of the standard sand |
本文针对两种典型工况研究动剪切模量比和阻尼比的共振柱试验误差问题.
普通组试验由10名经过培训的科技人员完成,为普通试验人员,代表着初等级别的试验结果;专业组试验由1人完成,为具有丰富经验的专业试验人员,代表着高等级别的试验结果.普通组和专业组,代表着试验群体的两种典型情况,为离散性最大和离散性最小的极端情况.其他情况,如10名普通试验人员与10名专业试验人员的对比、1名普通试验人员与1名专业试验人员的对比等,都不代表试验极端情况,其对比结果的离散性应该在上述两个极端情况之间.
普通组中每个试验人员分别进行4次试验,即得到试验数据40组;工况二中试验人员分别进行40次试验.每人(次)试验中,砂土均需要重新制样,制样方法按照《土工试验规程》(GB/SL237-1999)[15]进行.
动剪切模量比和阻尼比与剪应变是非线性关系.共振柱试验得到的小中应变下的结果,对中大应变下的曲线采用公认的双曲线模型得到,双曲线模型参数由试验点回归确定.确定8个典型剪应变5×10-6、10-5、5×10-5、10-4、5×10-4、10-3、5×10-3和10-2下动剪切模量比和阻尼比.
2 试验结果及可靠性普通组和专业组的剪切模量比和阻尼比试验结果如图 1所示.
|
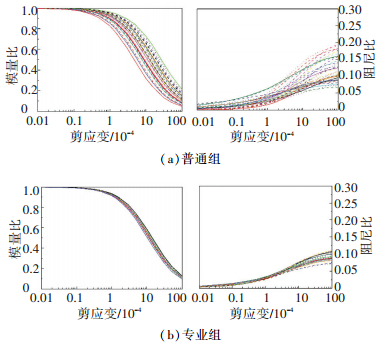
图 1 动剪切模量比和阻尼试验结果 Figure 1 Test results of shear modulus ratios and damping ratios |
从试验结果看,专业组的试验结果很正常,但普通组个别曲线离散较大,特别是阻尼比的情况.考虑到以往经验中,阻尼比试验的稳定性一般要小于模量试验,因此本文没有将阻尼中离散较大的试验点作为异常点去掉,仍然纳入到统计数据中.
根据统计学中的异常值检验经验方法[16],上述各个曲线超过97%的试验结果落在均值2倍标准差范围内,超过95%的基准值要求,故试验结果可靠、可用.
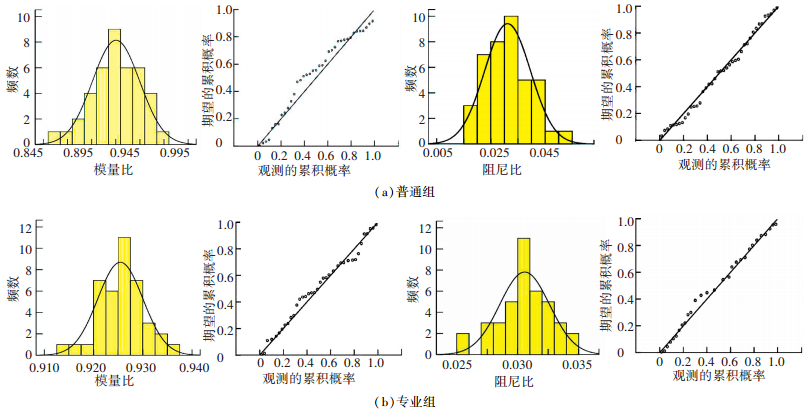
3 试验误差分布形态采用频数直方图和P-P图法确定8个典型剪应变下动剪切模量比和阻尼比的分布形态.普通组和专业组在剪应变为10-4时的剪切模量比和阻尼比的频数直方图和P-P图结果如图 2所示,从图中可见,动剪切模量比和阻尼比在剪应变为10-4时均服从正态分布,其他剪应变下结果类同.为给出定量结果,本文采用统计学权威软件SPSS进行正态性检验,给出采用Shapiro-Wilk检验的P值,结果如表 2所示.统计学中P值大于0.05,即认为数据服从正态分布,因此10-4时动剪切模量比和阻尼比均为正态分布,其他剪应变下结果类同.
|
图 2 剪应变为10-4时剪切模量比和阻尼比的频数分布图和P-P检验图 Figure 2 Frequency distribution and test results and P-P of test results for shear modulus ratio and damping ratio at strain of 10-4 |
| 表 2 SPSS软件对剪应变10-4时试验数据正态性检验P值 Table 2 Normality test of P value at strain of 10-4 using SPSS |
采用统计分析方法,以最大值、最小值、均值、标准差、一倍标准差、变异系数以及不同概率水准等指标来描述土样在8个典型剪应变下动剪切模量比和阻尼比的离散性.其中,均值反应一组变量的平均水平,设共有N个原始数据,Xi为第i个原始数据,则均值为
| $ \bar X = \frac{1}{N}\sum\limits_{i = 1}^N {{X_i}} . $ |
标准差S反应一组数据的平均离散水平,公式为
| $ S = \sqrt {\frac{{\sum\limits_{i = 1}^N {{{\left( {{X_i} - \bar X} \right)}^2}} }}{{N - 1}}} $ |
变异系数CV反应计量资料的离散程度,公式为
| $ {\rm{CV = }}\frac{S}{{\bar X}} \times 100\% . $ |
参考值范围本文采用双侧界值,对于正态分布(或者近似正态分布),参考值范围上下限计算公式为
| $ \bar X \pm {\mu _{\frac{\alpha }{2}}}S. $ |
对于图 1的试验结果,针对8个典型剪应变,计算出普通组和专业组的动剪切模量比和阻尼比的极大值、极小值、均值、标准差、一倍标准差以及变异系数等指标,结果见表 3和表 4.
| 表 3 模量比误差分析结果 Table 3 Error analysis results of dynamic shear modulus ratio |
| 表 4 阻尼比误差分析结果 Table 4 Error analysis results of damping ratio |
由表 3和表 4可知,普通组和专业组的动剪切模量比和阻尼比试验都有离散性,但普通组动剪切模量比和阻尼比试验的离散性指标远大于专业组的指标.
5 试验结果离散性分析 5.1 均值及其置信区间就均值而言,无论动剪切模量比还是阻尼比,普通组与专业组的试验结果都十分接近,但二者均值的置信区间有不同之处.普通组与专业组的砂土动剪切模量比和阻尼比试验均值偏差的95%置信区间示于表 5和表 6.
| 表 5 剪切模量比均值偏差的95%置信区间 Table 5 The confidence interval of the averaged shear modulus ratio with 95% deviation |
| 表 6 阻尼比均值偏差的95%置信区间 Table 6 The confidence interval of the averaged damping ratio with 95% deviation |
均值置信区间代表了均值可能的偏差程度,也是试验结果稳定性的表征之一.由表 5和表 6可知,试验结果是稳定的.但同时可以看出,专业组较普通组明显稳定,动剪切模量比较阻尼比稳定;专业组95%置信区间基本在±5%,均值可达到一个非常稳定的状态.需要说明的是,对于普通组试验,在小剪应变时,阻尼比95%置信区间超过±20%,说明在小剪应变时阻尼比的准确值不易得到,但是,因为小剪应变阻尼比的值很小,略一变动,置信区间就会有很大变化.例如,小剪应变阻尼比均值为0.01,置信区间20%时极限值为0.012,这样的偏差不会对地震动的计算结果造成影响.
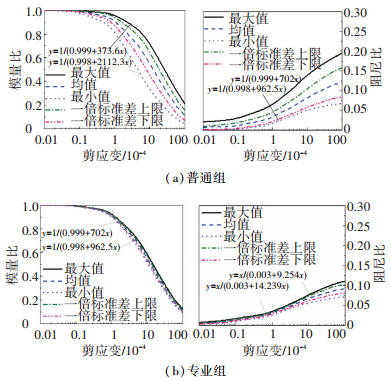
5.2 一倍标准差和包络线将表 3和表 4中动剪切模量比和阻尼比的一倍标准差曲线、外包线(极大值和极小值)曲线及其方程以及均值曲线示于图 3.
|
图 3 动剪切模量比和阻尼比均值、一倍标准差和外包线曲线 Figure 3 Mean values, standard deviation and envelopes curves for dynamic shear modulus ratio and damping ratio |
从图 3看出,普通组动剪切模量比和阻尼比的外包线方程相差很大,而专业组的方程相差很小,说明专业组和普通组试验精度差异显著.从图 3也可看出,普通组试验的一倍标准差与均值、外包线与一倍标准差之间均差别明显,而专业组差别则很小,表明普通组试验离散性明显大于专业组,说明专业组的试验误差很小,也说明试验人员因素、试验技术水平对试验结果可靠性影响很大.
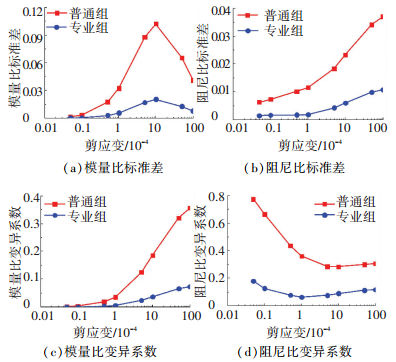
5.3 标准差和变异系数将表 3和表 4中动剪切模量比和阻尼比的标准差、变异系数与剪应变关系曲线示于图 4.
|
图 4 剪切模量比和阻尼比的标准差和变异系数与剪应变关系 Figure 4 Relationships of standard deviation and variation coefficients of shear modulus ratio and damping ratio with respect to shear strain |
由图 4可以看出,动剪切模量比和阻尼比试验离散性的统计指标均呈现出规律性,普通组与专业组趋势一致,只是数值不同.模量比标准差的最大值均出现在剪应变10-4~10-3范围,此范围恰是土层地震反应分析计算中动剪切模量比最常出现的区间.随着剪应变的增长,模量比的变异系数也呈现增长趋势,表明应变较小时动剪切模量比的离散性小,应变大时动剪切模量比的离散性明显增大;阻尼比的变异性系数随着剪应变的增长呈现下降趋势,表明小应变时阻尼比的离散性大,大应变时阻尼比的离散性小.
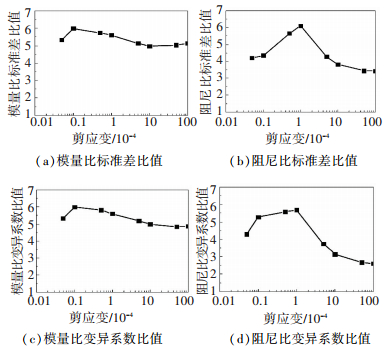
5.4 普通组与专业组试验离散性的对比为了更好地在量化上比较普通组试验和专业组试验离散性差别的大小,将普通组试验的剪切模量比和阻尼比的标准差、变异系数与专业组试验的标准差、变异系数相除,其比值见图 5.
|
图 5 普通组与专业组剪切模量比和阻尼比试验的标准差比值和变异系数比值 Figure 5 Relationships of standard deviation ratios and variation coefficient ratios of shear modulus ratio and damping ratio with respect to shear strain |
由图 5可知,对砂土试验,普通组与专业组标准差比值和变异系数比值表现基本相同,就模量比而言,比值在5左右,且随剪应变波动较小;就阻尼比而言,比值在4.5左右,且随剪应变波动较大,10-4时最大.这些结果表明,不同人员、不同水平对土的动剪切模量比和阻尼比试验误差影响非常显著.
5.5 剪切模量比和阻尼比变异性比较为了更好地比较动剪切模量比和阻尼比离散性差别的大小,将动剪切模量比和阻尼比的变异系数对比示于图 6.

|
图 6 剪切模量比和阻尼比变异系数的对比 Figure 6 Comparison between the variation coefficients of shear modulus ratio and damping ratio |
由图 6可知,无论是普通组还是专业组,模量比变异系数明显小于阻尼比变异系数,说明动剪切模量比试验的偏差程度小于阻尼比的结果.需要注意的是,从共振柱试验结果中,先进行动剪切模量比的拟合,然后以其结果为基础,加上从试验数据中确定出λmax,再进行阻尼比拟合.本文认为,阻尼比的离散实际上包括两部分,一是动剪切模量比的试验误差,二是确定λmax的误差,这样就可能造成了阻尼比变异系数要大于模量比变异系数.另外,由图 6再次可见,普通组与专业组变异系数相差甚大.
5.6 试验误差对地震反应分析影响的初步评价动剪切模量比和阻尼比的重要应用之一是为土层地震反应分析提供计算参数.根据以往的计算分析[17]可知,在剪应变为5×10-4时,中强地震下动剪切模量比6%的变异就会对地震动的计算结果产生不可忽视的影响.由图 6和表 3可知,在剪应变大于5×10-4时,普通组动剪切模量比的变异系数在12%以上,超过了可忽视的误差范围,其对地震动的影响将不可忽略.对于专业组的试验,在剪应变大于5×10-3时,砂土动剪切模量比的变异系数在6%~8%之间.由此初步估计,普通组的试验误差在中强震作用时不可忽略,而专业组试验的误差在强震作用时可能会有影响.
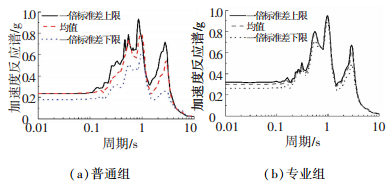
动剪切模量比和阻尼比的变异对地震动计算结果的影响是一个复杂的非线性问题,需要专门研究,这里仅给出两个典型算例.采用国际上通用的一维土层等效线性化程序SHAKE2000,一个三类场地为研究对象,输入波选用加速度峰值为0.4g的El Centro波,以普通组和专业组动剪切模量比和阻尼比均值为基准,分别计算动剪切模量比和阻尼比的一倍标准差上下限对反应谱的影响,计算结果分别如图 7和图 8所示.
|
图 7 动剪切模量比试验误差对地表加速度反应谱的影响 Figure 7 Influence of dynamic shear modulus ratio test error on surface response spectra |
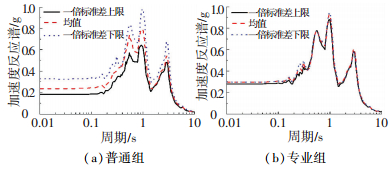
|
图 8 阻尼比试验误差对地表加速度反应谱的影响 Figure 8 Influence of damping ratio test error on surface response spectra |
由图 7和图 8可知,普通组试验误差对地表加速度反应谱的影响是不可忽略的,专业组试验误差的影响基本可以忽略.另外,无论普通组还是专业组,虽然本文上面的分析结果表明阻尼比试验误差要大于动剪切模量比试验误差,但就对地震反应分析的影响来说,反而是动剪切模量比试验误差对地表加速度反应谱要大于阻尼比试验误差的影响.需要说明的是,这里考虑的情况与实际还有很大差距,除砂土以外其他土类的试验误差,一类、二类和四类场地,其他类型的地震波输入等,都需要分门别类的详细分析.
5.7 误差来源分析上面的试验和分析结果都表明,普通组试验的离散性明显大于专业组的结果,表明不同试验人员、不同技术水平对土的动剪切模量比和阻尼比试验误差影响是非常显著的.综合分析,共振柱动剪切模量比和阻尼比试验误差主要来自以下几个个方面:
1) 制样差异,包括试样的成样质量和密度控制,这与祝龙根等[11]的观点和孙静等[18]的理论推导一致.根据本文试验经验,将此具体化为:落锤不垂直、测量每层土样高度的读数误差引起的试样密实度不均匀、试样表层平整度的差异、读数误差产生的土样整体高度的不同等,这方面普通组人员更易出问题.
2) 试验人员技术水平,包括试验装样的熟练程度、试验过程中对土样的扰动程度、刀片插入土中的深度等,这方面普通组人员显然有缺欠.
3) 橡皮膜影响,新橡皮膜将会使土样高度增大,直径变小.
6 结论1) 根据统计学中的异常值检验经验方法,所有试验曲线超过97%的结果落在均值2倍标准差范围内,超过了95%的基准值要求,试验结果可以用于概率分析.
2) 不同类型组的试验数据均服从正态分布,动剪切模量比和阻尼比试验离散性的统计指标均呈现出规律性,而且无论是普通组与专业组,其规律性是一致的,只是数值不同.
3) 模量比变异系数明显小于阻尼比变异系数,原因可能是阻尼比的离散既包括了动剪切模量比的试验误差又含有从试验数据确定阻尼比的误差,这样就造成了阻尼比试验的偏差程度大于动剪切模量比.
4) 普通组与专业组动剪切模量比和阻尼比试验均值十分接近,且均值置信区间均稳定可靠,说明普通组与专业组的试验均可能接近真值,但普通组比专业组的置信区间要大,表明技术熟练的试验人员的试验更容易接近真值.
5) 从外包线、一倍标准差、均值之间的距离来看,与专业组相比,普通组试验离散性明显大,二者动剪切模量比变异系数比值与阻尼比变异系数比值均约在5左右,说明试验人员因素及试验技术水平对试验结果可靠性影响十分显著.
6) 普通组砂土试验误差对中强地震动计算的影响不可忽略,专业组砂土试验误差基本可以忽略,但其他类型土以及更多场地和地震动输入的结果有待进一步研究.
| [1] |
李小勇, 谢康和, 虞颜. 太原粉质黏土强度指标概率特征[J].
浙江大学学报(工学版),2001, 35 (5) : 492-496.
LI Xiaoyong, XIE Kanghe, YU Yan. Probabilistic characteristics of strength indexes for Taiyuan siltyclay[J]. Journal of Zhejiang University (Engineering Science),2001, 35 (5) : 492-496. |
| [2] |
倪万魁, 韩启龙. 黄土土性参数的统计分析[J].
工程地质学报,2001, 9 (1) : 62-67.
NI Wankui, HAN Qilong. Statistical analysis of physical and mechanical indexes of the typical loess[J]. Journal of Engineering Geology,2001, 9 (1) : 62-67. |
| [3] | HARDIN B O, DRNEVICH V P. Shear modulus and damping in soils: measurement and parameter effects[J]. Journal of the Soil Mechanics and Foundations Division,1972, 98 (6) : 603-624. |
| [4] | WEN K L. Non-linear soil response in ground motions[J]. Earthquake Engineering and Structural Dynamics,1994, 23 (6) : 599-608. DOI: 10.1002/(ISSN)1096-9845 |
| [5] | BOULANGER R W, IDRISS I M. Evaluation of cyclic softening in silts and clays[J]. Journal Geotechnical and Geoenvironmental Engineering,2007, 133 (6) : 641-652. DOI: 10.1061/(ASCE)1090-0241(2007)133:6(641) |
| [6] |
孙静, 袁晓铭, 孙锐. 土动剪切模量和阻尼比的推荐值和规范值的合理性比较[J].
地震工程与工程振动,2004, 24 (2) : 126-133.
SUN Jing, YUAN Xiaoming, SUN Rui. Reasonability comparison between recommended and code values of dynamic shear modulus and damping ratio of soils[J]. Earthquake Engineering and Engineering Vibration,2004, 24 (2) : 126-133. |
| [7] |
陈国兴, 刘雪珠, 王炳辉. 土动力参数变异性对深软场地地表地震动参数的影响[J].
防灾减灾工程学报,2007, 27 (1) : 1-10.
CHEN Guoxing, LIU Xuezhu, WANG Binghui. Effect of variability of soil dynamic parameters on ground motion parameters for deep soft sites[J]. Journal of Disaster Prevention and Mitigation Engineering,2007, 27 (1) : 1-10. |
| [8] | HARDIN B O, BLACK W L. Vibration modulus of normally consolidated clay[J]. Journal of Soil Mechanics and Foundations Division,1968, 94 (2) : 353-369. |
| [9] | ZHANG Jianfeng, ANDRUS R D, JUANG C H. Normalized shear modulus and material damping ratio relationships[J]. Journal of Geotechnical and Geoenvironmental Engineering,2005, 131 (4) : 453-464. DOI: 10.1061/(ASCE)1090-0241(2005)131:4(453) |
| [10] |
GB 17741-2005工程场地地震安全性评价技术规范[S].北京:中国标准出版社, 2005.
GB 17741-2005. Code for seismic safety evaluation of engineering sites[S]. Beijing: Chinese Standard Press, 2005. http://www.oalib.com/references/17229040 |
| [11] |
祝龙根, 杜坚. 不同类型共振柱仪对比实验[J].
水电自动化与大坝监测,1990 (3) : 26-32.
ZHU Longgen, DU Jian. Comparison tests with different types of resonant column devices[J]. Hydropower Automation and Dam Monitoring,1990 (3) : 26-32. |
| [12] | AGUIRRE J. Nonlinearity, liquefaction and velocity variation of soft soil layers in Port Island, Kobe, during the Hyogo-ken-Nanbu earthquake[J]. Bulletin of the Seismological Society of America,1997, 87 (5) : 1244-1258. |
| [13] |
孙锐, 袁晓铭, 刘晓健. 动剪切模量比与剪切波速对地震动影响及等量关系研究[J].
岩土工程学报,2009, 31 (8) : 1267-1274.
SUN Rui, YUAN Xiaoming, LIU Xiaojian. Effects of dynamic shear modulus ratio and velocity on surface ground motion and their equivalent relations[J]. Chinese Journal of Geotechnical Engineering,2009, 31 (8) : 1267-1274. |
| [14] | MARTIN P P, SEED H B. One-dimensional dynamic ground response analyses[J]. American Society of Civil Engineering,1982, 108 (7) : 935-954. |
| [15] |
GB/SL237—1999土工实验规程[S].北京:中华水利水电出版社, 1999.
GB/SL237—1999. Specification of soiltest[S]. Beijing: China Water & Power Press, 1999. |
| [16] |
梁冯珍, 关静, 等.
统计学[M]. 北京: 机械工业出版社, 2014 .
LIANG Fengzhen, GUAN Jing, et al. Statistics for Engineers and the Sciences[M]. Beijing: China Machine Press, 2014 . |
| [17] |
刘晓健.土动力性能对地震动影响研究及测试标准初探[D].哈尔滨, 中国地震局工程力学研究所, 2007.
LIU Xiaojian. Effect of soil dynamic feature on ground motion and its testing standard[D]. Harbin: Institute of Engineering Mechanics, China Earthquake Administration, 2007. http://cdmd.cnki.com.cn/article/cdmd-85406-2009057366.htm |
| [18] |
孙静, 袁晓铭, 陶夏新. 共振柱试验机试验误差分析[J].
哈尔滨工业大学学报,2007, 39 (4) : 510-513.
SUN Jing, YUAN Xiaoming, TAO Xiaxin. Error analysis of resonant column device tests[J]. Journal of Harbin Institute of Technology,2007, 39 (4) : 510-513. |
 2016, Vol. 48
2016, Vol. 48


