钢结构由于其良好的力学性能、经济性能和使用性能被广泛地应用于大型桥梁、海上采油平台、工业与民用建筑领域,其良好的延性更是抗震设计的首选,但若长期处于如土壤、大气、酸雨、海洋环境等腐蚀环境下,均会出现腐蚀损伤现象[1].
腐蚀必然会导致材料各项力学性能发生不可逆转的退化,目前有学者通过研究锈蚀钢板[3]单调力学性能退化规律发现,锈蚀不仅造成试件截面减少、表面特征发生变化,还引起钢材屈服强度、极限强度和延性降低,且对延性影响更为明显.而延性的降低使得研究腐蚀钢结构的抗震性能显得尤为重要,低周往复荷载作用下钢材塑性本构模型[4-10]是钢结构抗震性能分析的基础.目前尚未发现文献涉及低周往复荷载作用下锈蚀钢材损伤累积及其循环塑性本构模型研究,低周往复荷载作用下钢材滞回循环属于低周疲劳,锈蚀对低周往复荷载作用下钢材塑性变形、裂纹扩展、断裂韧性影响会十分明显.
因此,为研究中性盐雾环境下不同腐蚀程度钢板的滞回性能退化规律及循环塑性本构模型,本文首先将对工程常见Q235钢板进行加速腐蚀,并对腐蚀后的试件进行循环加载试验,根据试验结果分析钢材的滞回性能,采用Ramberg-Osgood模型拟合不同腐蚀程度下钢材的循环骨架曲线,分析随腐蚀程度变化时相应参数变化规律,最后建立滞回本构模型,可为钢结构的抗震特性研究提供基础性数据.
1 试验概况 1.1 腐蚀试验为研究实际工程已经发生或可能发生的金属大气腐蚀问题及有关理论问题,目前已采用的加速试验方法包括湿热、盐雾、周期喷雾复合腐蚀、干湿周浸循环和多因子复合加速腐蚀试验等.研究表明[11],加速腐蚀试验与长期自然暴露试验相关性良好,且试验周期短,试验结果重现性较好,但试验条件及环境因素与自然环境相差较大,很难完全模拟.
根据GB/T 10125—2012[12]和GB/T 24517—2009 [13],为了得到盐雾环境下不同腐蚀状态下的钢板,采用人工喷雾加速法.其中NaCl溶液质量浓度为50 mg/L,PH值为6.2~7.2.将编号为A01-A71的8组板材试样(280 mm×50 mm×8mm)与垂直方向成45°自然暴露放置于屋顶箱体内,将配置好的氯化钠溶液倒入喷壶中,而外界环境温湿度处于本地区自然气候,每隔2~3 d将溶液以雾状喷在试件两侧,为了保证试件两面腐蚀均匀,试验每进行一次翻一次.取样时间分别为第1组(A1i):30 d,第2组(A2 i):110 d,第3组(A3i):150 d,第4组(A4i):250 d,第5组(A5i):310 d,第6组(A6i):370 d,第7组(A7i):440 d,总试验时间为440 d.其中i取值1、2、3,i=1时代表用于低周往复试验的试件,i=2、3时代表用于单调试验的试件.每腐蚀一组后进行除锈,并采用质量损失率来评定钢板腐蚀程度.
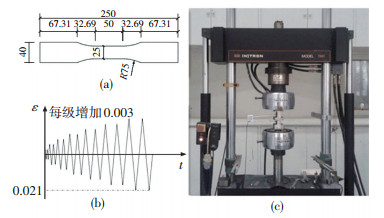
1.2 循环荷载试验加工试件图纸及加工完试件尺寸见图 1(a).加载装置采用Instron Model1341拉压扭万能疲劳试验机,其中位移计标距为50 mm,其量程在受拉方向为50%,受压方向为10%, 见图 1(c).为了防止板材在较大压应变作用下发生侧向屈曲变形,设计防屈曲装置.试件采用应变控制,进行大应变循环加载,以0.3%的增幅进行变幅加载,每级荷载循环两次,所有循环加载波形为三角波,应变加载速率0.000 25/s.当压应变达到2.1%时,不再施加循环荷载,而后对试件施加单向拉伸荷载,直到试件断裂,循环加载制度示意图见图 1(b).
|
图 1 试件尺寸、试验加载装置及制度图 Figure 1 Size of specimens/device and system for loading |
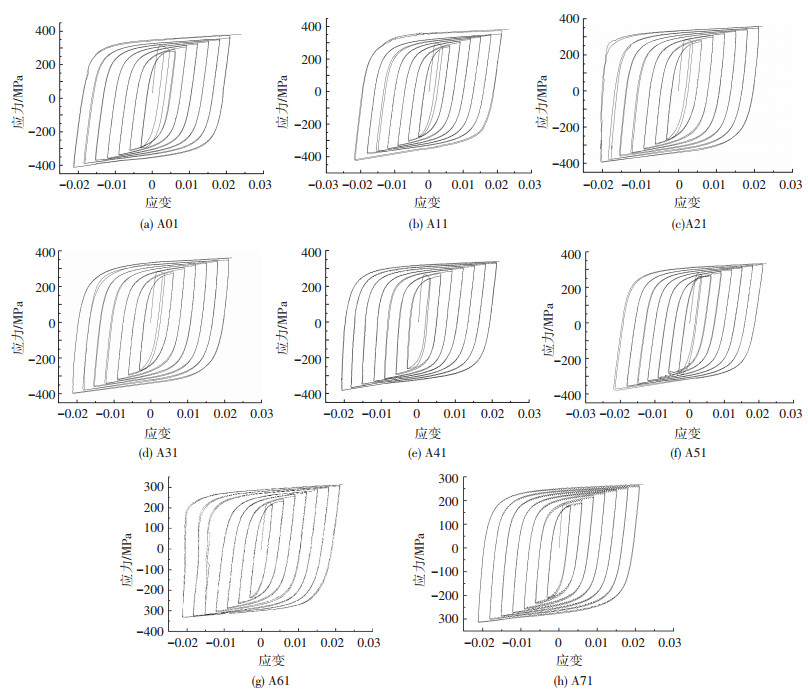
由于钢板锈蚀后,其表面凹凸不平,很难得到钢材的真实强度,为了客观地反应锈蚀对钢材滞回性能的影响,本文采用名义应力,即实际荷载与设计面积的比值.图 2为所有试件循环应力-应变曲线.
|
图 2 试件循环应力-应变曲线 Figure 2 Cyclic stress-strain curve of specimen |
从图 2可以看出,滞回曲线主要由骨架曲线、卸载曲线以及再加载曲线三部分组成.个别曲线出现不规则变化,可能是防屈曲装置与位移计产生轻微擦碰有关.钢材的首次加载曲线沿着单调拉伸曲线进行,为单向拉伸效应;钢材的卸载按照弹性直线卸载,随着应变的增加,各级循环的卸载曲线弹性模量略有降低;钢材再加载曲线的指向满足峰值指向模型;钢材下一级循环加载的峰值应力对上一级循环有较大依赖性;随着应变增加,钢材出现循环硬化效应,受拉方向的强化效应比受压方向强化效应更明显;在相同的应变幅下,后一圈的应力均大于前一圈的应力,表现出应力强化现象;未锈蚀钢材与锈蚀钢材的滞回环均比较饱满,表明锈蚀钢材同样具有较好的抗震耗能性能.
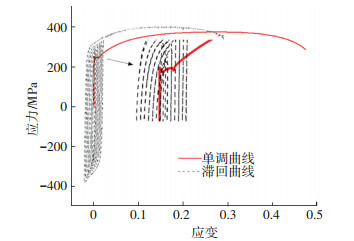
图 3为未锈蚀钢材在单调荷载及低周往复荷载下的应力-应变曲线.滞回曲线与单调曲线最大的区别就在于屈服效应的不存在,同时钢材在循环荷载下强化效应提前,应力峰值点和钢材断裂点变化较大.通过对两种不同的加载制度对比发现,循环荷载下钢材的极限强度和断裂强度所对应的应变及断裂伸长率相对于单调曲线要低很多,说明钢材在循环荷载下的累计损伤效应对其延性具有较大的影响.
|
图 3 未腐蚀钢材单调和滞回曲线对比 Figure 3 Monotonic and hysteretic curves of non-corrosive steel |
表 1汇总了试件试验的主要力学性能参数.表中fu为极限强度,εu为极限应变.从表 1可以看出随着腐蚀程度增加,钢材在循环荷载下的极限强度呈降低趋势,并且极限强度对应的应变及断后伸长率整体亦呈减小趋势;试验过程中部分锈蚀试件在其达到最大强度时便发生断裂,说明在循环荷载下锈蚀钢材的延性严重退化.将腐蚀率与滞回能关系进行拟合
| $ J=64.499\times \exp \left(-{{\rho }_{\text{w}}}/13.541 \right)+189.905, $ | (1) |
式中:J指滞回能,ρw为腐蚀率(质量损失率).可以看出,在相同的滞回圈数下,随着腐蚀程度的增加,钢材抗震耗能性能呈指数降低.
| 表 1 试件主要力学性能参数汇总表 Table 1 Summary on mechanical properties of the specimen |
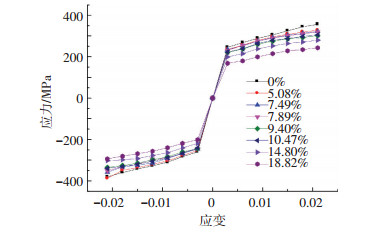
图 4为不同锈蚀程度下钢材的循环应力-应变骨架曲线.可以看出钢材在循环荷载作用下存在明显的循环硬化现象,且不存在屈服平台.与未锈蚀钢材相比,锈蚀钢材的强度均出现降低,锈蚀程度越大,强度下降程度越明显.
|
图 4 不同锈蚀程度下钢板滞回骨架曲线 Figure 4 Hysteresis curve on varying degrees of corrosion steel |
利用试验所得每一级循环加载下的最大正应力及正应变,并结合Ramberg-Osgood模型,对不同锈蚀程度下钢材的滞回骨架曲线进行拟合.Ramberg-Osgood模型数学表达式为
| $ \frac{\vartriangle \varepsilon }{2}=\frac{\vartriangle {{\varepsilon }_{\text{e}}}}{2}+\frac{\vartriangle {{\varepsilon }_{\text{p}}}}{2}=\frac{\vartriangle \sigma }{2E}+{{\left( \frac{\vartriangle \sigma }{2K'} \right)}^{1/n'}}, $ | (2) |
式中:Δε为总应变幅,Δεe为弹性应变幅,Δεp为塑形应变幅,E为钢材的弹性量,K′为循环强化系数,n′为循环强化指数,Δσ为稳定的应力幅,下同.
为了便于计算和比较,对上式进行简化变形,具体数学表达式为
| $ \varepsilon =\frac{\sigma }{E}+{{\left( \frac{\sigma }{2K'} \right)}^{1/n'}}. $ | (3) |
利用式(3)对循环加载骨架曲线进行拟合,K′和n′的具体拟合值见表 2,拟合曲线见图 5(以A01、A41及A71为例),从图 5曲线的拟合程度可知,采用Ramberg-Osgood模型对循环骨架曲线的拟合效果比较理想.
| 表 2 骨架曲线模型参数 Table 2 Skeleton curve model |

|
图 5 骨架曲线拟合模型 Figure 5 Fitting curve of skeleton model |
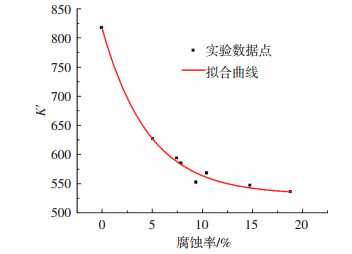
不同锈蚀程度下的K′见图 6.随着锈蚀钢板腐蚀率的增加,钢材循环强化系数呈现减小的趋势,而循环强化指数变化规律不明显.根据指数函数的意义,循环强化系数减小说明了随着钢材锈蚀程度的加重,钢材在循环荷载下其强化效应减弱.根据图 6分析得到K′与钢板腐蚀率之间的关系为
|
图 6 循环强化系数K′与腐蚀率关系 Figure 6 Relationship between recycling intensified factor K′ and corrosion rate |
| $ K'=\text{285}\text{.926}\times \text{exp}\left(-{{\rho }_{w}}/0.046 \right)+531.090. $ |
对于循环强化指数n′,变化规律不明显,未腐蚀钢板为0.211,腐蚀率达到19%的钢板为0.201,锈蚀率在18%以内时,n′为0.16n,其中n可取值范围为0.95~1.05.
3 钢板循环本构模型从图 2可看出,滞回曲线主要由骨架曲线、卸载曲线以及再加载曲线三部分组成.其中钢材的首次加载及峰值指向参见2.2及3.1节,卸载刚度(初始弹性模量Es)见表 2.
3.1 循环骨架准则虽然Ramberg-Osgood模型可以较为准确地模拟循环骨架曲线的形状,但是此函数不包含屈服点,对于屈服位置的判断不明确,并且应变是应力的函数,其反函数难以求得,不利于滞回准则的实现.因此可提出两段式循环骨架曲线:第一阶段在钢材屈服之前,为弹性部分;第二阶段是循环强化部分,具体表达为
| $ \sigma =\left\{ \begin{matrix} {{\sigma }_{\text{y}}}, & \varepsilon \le {{\varepsilon }_{\text{y}}}; \\ a+b\times {{e}^{\left( c\times \varepsilon \right)}}, & \varepsilon >{{\varepsilon }_{\text{y}}}. \\ \end{matrix} \right. $ |
式中:参数a,b,c用于控制循环骨架曲线的形状.由于循环荷载下屈服效应不明显,屈服强度不容易确定,而在以往的腐蚀钢板单调性能研究中,未腐蚀与腐蚀钢板的屈服强度所对应的应变在0.001 2~0.001 3,本文取应变0.001 2所对应的应力作为屈服强度.以A11为例,试验及模型对比见图 7,可看出提出的函数形式可对Q235不同腐蚀率下的循环受力特征进行很好地模拟,能够较好反映循环骨架曲线.

|
图 7 A11循环骨架模型曲线 Figure 7 Model for skeleton curve of A11 |
根据腐蚀率及滞回曲线试验数据,可得到循环骨架曲线参数与腐蚀率关系:
σy=-23.898×e(-ρw/-12.612)+260.006,
a=234.421×e(-ρw/4.961)+305.723,
b=-148.302-169.314×0.651ρw.
其中系数c变化规律不明显,除未腐蚀试件为-26.7外,其余不同腐蚀率下可取-62.2 K,其中K可取值范围为0.70~1.20.
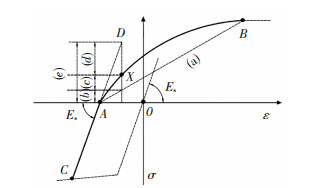
3.2 再加载准则本文再加载曲线参照文献[7]在论文中提出的计算模型,结合本文试验结果对模型进行了部分修正,见图 8.
|
图 8 再加载曲线模型 Figure 8 Reloading curve model |
如图 8所示,CA段为卸载曲线,AB段为受拉再加载曲线.其中A点为再加载曲线的起点(εAi,0),εAi定义为位移加载制度中相对应的数值;B点为再加载曲线的目标点(εbi,σbi),定义为每级循环受拉对应的最大值,可参照骨架曲线准则模型;C点为受压再加载曲线目标点,定义为每级循环受压对应的最大值,可参照骨架曲线准则模型;Es为卸载斜率(刚度),可参见表 2;线a与ε轴所对应的角度为Ek;假设X点为所求应力,则线b为Ek(ε-εAi),线e为Es(ε-εAi),线c+d为(Es-Ek)(ε-εAi),假设线d占c+d线比例为η,则线d为η(Es-Ek)(ε-εAi).
因此图示X点应力:
| $ \left\{ \begin{matrix} \sigma ={{E}_{\text{s}}}\left( \varepsilon-{{\varepsilon }_{\text{A}}} \right)+{{\sigma }_{\text{A}}}-\left( {{E}_{\text{s}}}-{{E}_{\text{k}}} \right)\left( \varepsilon-{{\varepsilon }_{\text{A}}} \right)\eta, \\ {{E}_{\text{k}}}=\frac{{{\sigma }_{\text{B}}}-{{\sigma }_{\text{A}}}}{{{\varepsilon }_{\text{B}}}-{{\varepsilon }_{\text{A}}}}. \\ \end{matrix} \right. $ |
其中
| $ \eta =a-\frac{b}{\frac{\varepsilon-{{\varepsilon }_{\text{A}}}}{{{\varepsilon }_{\text{B}}}-{{\varepsilon }_{\text{A}}}}+b}. $ |
根据试验结果,系数a,b取值并没有特别的变化规律,a取值在1.05~1.4,b取值在0.05~0.6.
3.3 试验及模型对比综合上述几种准则及滞回曲线试验结果,滞回曲线发展准则见图 9:首次加载时曲线沿着单调拉伸O-A1曲线(参见2.2节及3.1节)进行,达到A1点屈服强度;按照循环骨架曲线的准则(参见3.1节)到达峰点A2;即达到钢材的卸载点后按弹性直线卸载至O1点(应变为峰值应力与弹性模量Es的比值),卸载刚度和初始弹性模量Es相同(参见表 2);然后在受压循环第一圈的时候指向的峰值为受压屈服点B1(参见3.2节);经过屈服点后,沿着受压骨架曲线前进,到达卸载点B2;直线卸载后到达再加载点-O1(应变为峰值应力与弹性模量Es的比值);受拉达到最大值A2后,然后进行第二圈,重复以上步骤(即卸载至O1点,压至B2点,卸载至-O1点),最终沿着骨架曲线经过A2点到达卸载点A3(参见3.2节);弹性卸载后到达受压再加载曲线起点O2,重复前述过程.

|
图 9 滞回准则具体描述 Figure 9 The specific description of the hysteresis criterion |
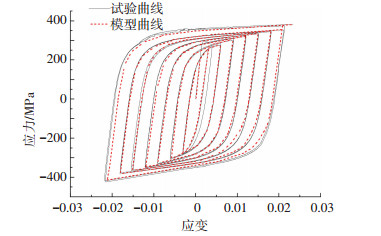
将采用循环本构模型计算的曲线与钢板试验循环加载的滞回曲线进行对比分析,以A11为例,见图 10所示,可见计算模型与试验结果基本吻合.说明本文中的钢材循环本构模型不仅可以较为准确地预测钢材在不同腐蚀率下的滞回性能,同时可以预测试件的剩余强度.
|
图 10 A11模型及试验数据对比 Figure 10 Comparison chart between model and experimental data of A11 |
1) 在循环荷载作用下,未腐蚀钢材与腐蚀钢材均出现循环硬化、峰值点指向效应等现象,并且滞回环比较饱满;且随着腐蚀程度增加,腐蚀钢材在循环荷载作用下各项力学性能呈现下降趋势,腐蚀钢材的延性劣化加重.
2) Ramberg-Osgood模型较好地拟合了腐蚀钢板在循环荷载下的骨架曲线,并且随着腐蚀程度增加,钢材循环强化系数呈现减小的趋势,但循环强化指数的变化规律并不明显.
3) 本文建立了腐蚀钢板循环本构模型,包括首次加载准则,卸载准则,循环骨架准则,再加载曲线准则等,且模型与试验结果对比基本吻合.因此本文提出的钢材循环本构模型不仅可以较为准确地预测钢材在不同腐蚀率下的滞回性能,同时可以预测试件的剩余强度.
| [1] |
侯保荣. 海洋环境下钢结构物浪花飞溅区的腐蚀灾害[J].
科学中国人,2006 (11) : 21-22.
HOU Baorong. Corrosion of steel structures in the marine environment[J]. Scientific Chinese,2006 (11) : 21-22. |
| [2] |
史炜洲, 童乐为, 陈以一, 等. 腐蚀对钢材和钢梁受力性能影响的试验研究[J].
建筑结构学报,2012, 33 (7) : 53-60.
SHI Weizhou, TONG Weile, CHEN Yiyi, et al. Experimental study on influence of corrosion on behavior of steel material and steel beams[J]. Journal of building structures,2012, 33 (7) : 53-60. DOI: 10.14006/j.jzjgxb.2012.07.006 |
| [3] |
邱斌, 徐善华. 锈蚀钢板力学性能的退化规律[J].
机械工程材料,2014, 38 (10) : 60-63.
QIU Bin, XUShanhua. Deterioration law of mechanical properties of corroded steel plates[J]. Materials for mechanical engineering, ,2014, 38 (10) : 60-63. |
| [4] |
石永久, 王萌, 王元清. 结构钢材循环荷载下的本构模型研究[J].
工程力学,2012, 29 (9) : 92-98.
SHI Yongjiu, WANG Meng, WANG Yuanqing. Study on constitutive model of structural steel under cyclic loading[J]. Engineering Mechanics,2012, 29 (9) : 92-98. |
| [5] | SHI Gang, WANG Meng, BAI Yu, et al. Experimental and modeling study of high-strength structural steel under cyclic loading[J]. Experimental and modeling study of high-strength structural steel under cyclic loading,2012 (37) : 1-13. DOI: 10.1016/j.engstruct.2011.12.018 |
| [6] |
罗云蓉, 王清远, 刘永杰, 等. Q235, Q345钢结构材料的低周疲劳性能[J].
四川大学学报(工程科学版),2012, 44 (2) : 169-175.
LUO Yunrong, WANG Qingyuan, LIU Yongjie, et al. Low cycle fatigue properties of steel structure materials Q235 and Q345[J]. Journal of Sichuan University (Engineering Science edition),2012, 44 (2) : 169-175. DOI: 10.15961/j.jsuese.2012.02.012 |
| [7] | SHI Yongjiu, WANG Meng, WANG Yuanqing. Experimental and constitutive model study of structural steel under cyclic loading[J]. J Constr Steel Res,2011, 67 (8) : 1185-1197. DOI: 10.1016/j.jcsr.2011.02.011 |
| [8] | APOSTOLOPULOS C A. Mechanical behavior of corroded reinforcing steel bars S500s tempcore under low cycle fatigue[J]. Construction and Building Materials,2007, 21 : 1447-1456. DOI: 10.1016/j.conbuildmat.2006.07.008 |
| [9] | APOSTOLOPULOS C A, PAPADOPOULOS M P. Tensile and low cycle fatigue behavior of corroded reinforcing steel bars S400[J]. Construction and Building Materials,2007, 21 : 855-864. DOI: 10.1016/j.conbuildmat.2005.12.012 |
| [10] | MEBDES LAM, CASTROA LMSS. A simplified reinforcing steel model suitable for cyclic loading including ultra-low-cycle fatigue effects[J]. Engineering Structures,2014, 68 : 155-164. DOI: 10.1016/j.engstruct.2014.02.031 |
| [11] | MELCHERS R E. Modeling of marine corrosion of steel specimens[M]//KAINR M, YOUNG W T. Corrosion testing in natural waters. Philadelphia: ASTM STP 1300, 1997:20-33. |
| [12] |
人造气氛腐蚀试验-盐雾试验:GB/T 10125—2012[S].北京:中国国家标准化管理委员会, 2012.
Corrosion tests in artificial atmospheres-Salt spray tests: GB/T 10125—2012[S]Beijing:Standards Press of China, 2012. |
| [13] |
金属和合金的腐蚀户外周期喷淋暴露试验方法:GB/T 24517—2009[S].北京:中国国家标准化管理委员会, 2009.
Corrosion of metals and alloys. Outdoors exposure test methods for periodic water spray: GB/T 24517—2009[S].Beijing: Standards Press of China, ,2009. |
 2016, Vol. 48
2016, Vol. 48


