2. 中电建路桥集团有限公司,北京 100048
2. Power China Road Bridge Group Co., Ltd., Beijing 100048, China
薄壁箱梁具有良好的抗弯和抗扭性能在现代桥梁中得到广泛应用.当箱梁发生竖向位移时,由于翼板中剪力滞后的影响引起翼板纵向应力沿横向分布不均匀,而存在剪力滞效应[1-5].
对于箱梁自由振动而言,剪力滞效应引起箱梁的动力特性发生显著变化.对于不同的跨高比,可忽略箱梁部分影响因素而建立相应的自由振动方程.当跨高比较大时,甘亚南等[6]、吴有俊等[7]以欧拉梁为基础,忽略了剪力滞引起纵向位移的惯性影响,分别研究了剪力滞引起的弹性势能对梁动力特性的影响.对于跨高比小的箱梁,此时截面的剪切变形和转动惯量影响不可忽略.张永健等[8]分析了剪切变形和剪力滞效应对简支箱梁自振频率的影响.甘亚南等[9-10]基于Timoshenko梁理论讨论了剪力滞效应对等截面箱梁自振频率的影响.周旺保等[11]研究了剪力滞、剪切变形、转动惯量、滑移效应对钢-混凝土组合箱型梁动力特性的影响.
在上述箱梁自由振动的求解过程中,大部分是基于分离变量法得到箱梁自由振动的解析解.由于箱梁的自由振动控制方程是一个微分方程组,因此自振频率超越方程及模态函数很复杂.从梁的振动方程角度看,剪力滞效应对梁振动的影响可看作是欧拉梁振动方程修正后形成的系统,则可以利用摄动法求解箱梁自由振动.楼梦麟[12]首先利用模态摄动法,将变系数微分方程的求解问题转化为代数方程组进行求解,从而简化了特征方程的求解.随后,楼梦麟等[13]、潘旦光等[14]将模态摄动法应用于变截面梁的振动.潘旦光等[15-16]进一步将模态摄动法推广到变截面Timoshenko梁振动方程的求解.本文将利用模态摄动法的基本思想,研究箱梁的自振频率和振型的简化分析方法.在此基础上,根据箱梁位移和弯矩的关系,推导了箱梁自由振动的模态剪力滞系数,并分析跨宽比和翼缘板的刚度占梁总刚度百分比等对梁模态剪力滞系数的影响.
1 箱梁的自由振动方程图 1所示的矩形薄壁箱型梁,若梁的竖向位移为w (x, t),上下翼缘板的纵向位移函数为vi(x, y, t),且假定vi(x, y, t)可表示为
| $ {v_i}\left( {x, y, t} \right) = {h_i}\left[{\frac{{{\rm{d}}w}}{{{\rm{d}}x}} + \left( {1-\frac{{{y^3}}}{{{b^3}}}u\left( {x, t} \right)} \right)} \right]. $ | (1) |

|
图 1 箱形梁截面 Figure 1 Cross section of box girder |
式中:u(x, t)为翼缘板剪切转角的最大差值,x、y和z分别表示顺梁方向、垂直于梁方向和竖向,b为箱室净宽的一半,hi截面形心到顶、底板的距离,i分别取顶、底板.
基于欧拉梁理论,梁的动能T为
| $ T = \frac{1}{2}{\int\limits_0^l {\rho A\left( {\frac{{\partial w}}{{\partial t}}} \right)} ^2}{\rm{d}}x + \frac{1}{2}{\int\limits_0^l {\rho {I_s}\left( {\frac{{\partial u}}{{\partial t}}} \right)} ^2}{\rm{d}}x. $ | (2) |
梁的势能V为
| $ \begin{array}{l} V = \frac{1}{2}\int\limits_0^l {EIw'{'^2}} {\rm{d}}x + \frac{1}{2}\int\limits_0^l {\frac{9}{5}\frac{G}{{{b^2}}}{I_s}{u^2}} {\rm{d}}x + \\ \;\;\;\;\;\frac{1}{2}\int\limits_0^l {E{I_s}\left( {\frac{3}{2}w''u' + \frac{9}{{14}}u{'^2}} \right)} {\rm{d}}x. \end{array} $ | (3) |
式中:ρ、E、G、A分别为箱梁的密度、弹性模量、剪切模量和截面面积.I为截面的转动惯量,Is为顶板和底板的转动惯量.根据Hamilton原理可得梁的自由振动方程为:
| $ \rho A\ddot w + EI{w^{\left( 4 \right)}} + \frac{3}{4}E{I_s}{u^{\left( 3 \right)}} = 0, $ | (4a) |
| $ \rho {I_s}\ddot u-\frac{3}{4}E{I_s}{w^{\left( 3 \right)}}-\frac{9}{{14}}E{I_s}u'' + \frac{9}{5}\frac{{G{I_s}}}{{{b^2}}}u = 0. $ | (4b) |
若式(4)所对应的第j阶模态的特征值为
| $ -{{\bar \lambda }_j}\rho A{{\bar W}_j} + EI{{\bar W}_j}^{\left( 4 \right)} + \frac{3}{4}E{I_s}{{\bar U}_j}^{\left( 3 \right)} = 0, $ | (5a) |
| $ {{\bar \lambda }_j}\rho {I_s}{{\bar U}_j}' + \frac{3}{4}EI{{\bar W}_j}^{\left( 4 \right)} + \frac{9}{{14}}E{I_s}{{\bar U}_j}^{\left( 3 \right)}-\frac{{9G{I_s}}}{{5{b^2}}}{{\bar U}_j}' = 0. $ | (5b) |
忽略剪力滞效应后,具有相同跨度欧拉梁第j阶模态的控制方程为
| $ -{\lambda _j}\rho A{W_j} + EI{W_j}^{\left( 4 \right)} = 0. $ | (6) |
当梁为简支梁时,与式(6)特征方程相对应的特征值和模态为
| $ {\lambda _j} = {\left( {\frac{{j{\rm{\pi }}}}{l}} \right)^4}\frac{{EI}}{{\rho A}}, \;\;{W_j} = \sin \left( {\frac{{j{\rm{\pi }}}}{l}x} \right). $ | (7) |
直接模态摄动法的基本思想是把式(5)考虑剪力滞效应薄壁箱梁的特征方程看成式(6)所表示的等截面欧拉梁经过参数修改所得到的新系统,这个新系统的主模态函数以及特征值可以用等截面欧拉梁的模态特征经过简单的摄动分析求解.则可以假设:
| $ {{\bar \lambda }_j} = {\lambda _j} + \Delta {\lambda _j}, $ | (8a) |
| $ {{\bar W}_j} = {W_j} + \sum\limits_{k = 1, k \ne j}^n {{W_k}{p_{kj}}, } $ | (8b) |
| $ {{\bar U}_j} = \sum\limits_{k = 1}^n {{W_k}'{q_{kj}}} . $ | (8c) |
从理论上来说,式(6)中梁有无穷多个主模态函数,即式(8)中n应该趋向于无穷.但是在实际计算时,通常只需要考虑有限个低阶模态进行近似的计算就可以满足要求.当解出Δλj,pkj,qkj这2n个未知数,即可计算箱梁的第j阶特征值及其对应的主模态函数.将(8)式代入(5)式可得:
| $ \begin{array}{l} -\left( {{\lambda _j} + \Delta {\lambda _j}} \right)\rho A\left( {{W_j} + \sum\limits_{k = 1, k \ne j}^n {{W_k}{p_{kj}}} } \right) + EI\left( {{W_j}^{\left( 4 \right)} + } \right.\\ \left. {\sum\limits_{k = 1, k \ne j}^n {{W_k}^{\left( 4 \right)}{p_{kj}}} } \right) + \frac{3}{4}E{I_s}\sum\limits_{k = 1}^n {{W_k}^{\left( 4 \right)}{q_{kj}}} = 0, \end{array} $ | (9a) |
| $ \begin{array}{c} \left( {{\lambda _j} + \Delta {\lambda _j}} \right)\rho {I_s}\sum\limits_{k = 1}^n {{W_k}''{q_{kj}}} + \frac{3}{4}E{I_s}\left( {{W_j}^{\left( 4 \right)} + \sum\limits_{k = 1, k \ne j}^n {{W_k}^{\left( 4 \right)}{p_{kj}}} } \right) + \\ \frac{9}{{14}}E{I_s}\sum\limits_{k = 1}^n {{W_k}^{\left( 4 \right)}{q_{kj}}}-\frac{{9G{I_s}}}{{5{b^2}}}\sum\limits_{k = 1}^n {{W_k}''{q_{kj}}} = 0. \end{array} $ | (9b) |
在方程(9)两边同时乘以Wi(x)(i=1, 2, ···n),然后沿全长积分,根据欧拉梁的模态正交性,化简后可得:
| $ \begin{array}{*{20}{l}} {-\left( {{\lambda _j} + \Delta {\lambda _j}} \right)\rho A\sum\limits_{k = 1, k \ne j}^n {{R_{ik}}{p_{kj}}} + EI\sum\limits_{k = 1, k \ne j}^n {{T_{ik}}{p_{kj}}-} }\\ {\Delta {\lambda _j}\rho A{R_{ij}} + \frac{3}{4}E{I_s}\sum\limits_{k = 1}^n {{T_{ik}}{q_{kj}}} = {\lambda _j}\rho A{R_{ij}}-EI{T_{ij}}, } \end{array} $ | (10a) |
| $ \begin{array}{l} \frac{3}{4}E{I_s}\sum\limits_{k = 1, k \ne j}^n {{T_{ik}}{p_{kj}}} + \rho {I_s}\left( {{\lambda _j} + \Delta {\lambda _j}} \right)\sum\limits_{k = 1}^n {{S_{ik}}{q_{kj}}} + \\ \frac{9}{{14}}E{I_s}\sum\limits_{k = 1}^n {{T_{ik}}{q_{kj}}}-\frac{{9G{I_s}}}{{5{b^2}}}\sum\limits_{k = 1}^n {{S_{ik}}{q_{kj}}} =-\frac{3}{4}E{I_s}{T_{ij}}. \end{array} $ | (10b) |
式(10)中:
| $ \begin{array}{c} {R_{ij}} = \int\limits_0^l {{W_i}{W_j}{\rm{d}}x} = \frac{l}{2}{\delta _{ij}}, \\ {S_{ij}} = \int\limits_0^l {{W_i}{W_j}{\rm{''d}}x} =-{\left( {\frac{{j{\rm{\pi }}}}{l}} \right)^2}\frac{1}{2}{\delta _{ij}}, \\ {T_{ij}} = \int\limits_0^l {{W_i}{W_j}^{\left( 4 \right)}{\rm{d}}x} = {\left( {\frac{{j{\rm{\pi }}}}{l}} \right)^4}\frac{1}{2}{\delta _{ij}}. \end{array} $ |
式中δij为Kronecker符号.
依次取i为1, 2, …,n,重复利用式(10)可得2n个代数方程.将2n个代数方程写成矩阵形式:
| $ \left( {\left[\begin{array}{l} {\mathit{\boldsymbol{C}}^{11}}{\mathit{\boldsymbol{C}}^{12}}\\ {\mathit{\boldsymbol{C}}^{21}}{\mathit{\boldsymbol{C}}^{22}} \end{array} \right] + \Delta {\lambda _j}\left[\begin{array}{l} {\mathit{\boldsymbol{D}}^{11}}0\\ 0{\mathit{\boldsymbol{D}}^{22}} \end{array} \right]} \right)\left\{ \begin{array}{l} \mathit{\boldsymbol{p}}\\ \mathit{\boldsymbol{q}} \end{array} \right\} = \left\{ \begin{array}{l} \mathit{\boldsymbol{M}}\\ \mathit{\boldsymbol{N}} \end{array} \right\}. $ | (11) |
式中:C11、C12、C21、C22、D11、D22都为n阶方阵,p、q、M、N为n阶向量.各个方阵和向量的元素分别为:
| $ \begin{array}{c} \mathit{\boldsymbol{C}}_{ik}^{11} = \left\{ {\begin{array}{*{20}{c}} {-{\lambda _j}\rho A{R_{ik}} + EI{T_{ik}}, }&{k \ne j;}\\ {-{\lambda _j}\rho A{R_{ik}}, }&{k = j.} \end{array}} \right.\\ \mathit{\boldsymbol{C}}_{ik}^{12} = \frac{3}{4}E{I_s}{T_{ik}}.\\ \mathit{\boldsymbol{C}}_{ik}^{21} = \left\{ {\begin{array}{*{20}{c}} {\frac{3}{4}E{I_s}{T_{ik}}, }&{k \ne j;}\\ {0, }&{k = j.} \end{array}} \right.\\ \mathit{\boldsymbol{C}}_{ik}^{22} = {\lambda _j}\rho {I_s}{S_{ik}} + \frac{9}{{14}}E{I_s}{T_{ik}}-\frac{{9G{I_s}}}{{5{b^2}}}{S_{ik}}, \\ \mathit{\boldsymbol{D}}_{ik}^{11} = \left\{ {\begin{array}{*{20}{c}} { - \rho A{R_{ik}}}&{k \ne j;}\\ {0, }&{k = j.} \end{array}} \right.\\ \mathit{\boldsymbol{D}}_{ik}^{22} = \rho {I_s}{S_{ik}}.\\ \mathit{\boldsymbol{p}} = {\left\{ {{p_{1j}} \cdots {p_{\left( {j - 1} \right)j}}\;\;\Delta {\lambda _j}/{\lambda _j}\;\;{p_{\left( {j + 1} \right)j}} \cdots {p_{nj}}} \right\}^{\rm{T}}}, \\ \mathit{\boldsymbol{q}} = {\left\{ {{q_{1j}}\;\;{q_{2j}}\;\; \cdots \;\;{q_{nj}}} \right\}^{\rm{T}}}, \\ {\mathit{\boldsymbol{M}}_i} = - EI{T_{ij}} + {\lambda _j}\rho A{R_{ij}}, \;\;{\mathit{\boldsymbol{N}}_i} = - \frac{3}{4}E{I_s}{T_{ij}}. \end{array} $ |
显然C11、C12、C21、C22、D11、D22都为对角矩阵,Mi=0,Ni=0(i≠j),因此,p、q只有第j个元素不为零,则式(11)只剩下两个方程.由此可得:
| $ {{\bar \lambda }_j}-\frac{3}{4}\frac{{{I_s}}}{I}{q_{jj}}{\lambda _j} = {\lambda _j}, $ | (12a) |
| $ {q_{jj}} = \frac{{-\frac{3}{4}E{I_s}{{\left( {\frac{{j{\rm{\pi }}}}{l}} \right)}^2}}}{{\frac{9}{{14}}E{I_s}{{\left( {\frac{{j{\rm{\pi }}}}{l}} \right)}^2} + \frac{{9G{I_s}}}{{5{b^2}}}-\rho {I_s}{{\bar \lambda }_j}}}. $ | (12b) |
将式(12b)代入式(12a)可得
| $ \frac{{{{\bar \lambda }_j}}}{{{\lambda _j}}} = 1-\frac{{\frac{{{j^2}{{\rm{\pi }}^2}}}{{{l^2}}}\left( {\alpha-1} \right)}}{{\alpha \frac{{{j^2}{{\rm{\pi }}^2}}}{{{l^2}}} + {\beta ^2}-\frac{{14}}{9}\frac{{\alpha \rho {{\bar \lambda }_j}}}{E}}} $ | (13) |
式中
由式(13)可得
| $ {{\bar \lambda }_j} = 0.5\xi-\sqrt {0.25{\xi ^2}-\eta }, $ | (14) |
式中
将式(14)代入式(12b)可得qjj的解为
| $ {q_{jj}} = \frac{{4I}}{{3{I_s}}}\frac{{{{\bar \lambda }_j}-{\lambda _j}}}{{{\lambda _j}}}. $ | (15) |
由式(14)可知,采用直接模态摄动法计算等截面箱梁振动特性式的计算结果与式(8)中n的选取无关.当n趋近于无穷时,式(8)中代表了全模态的展开,是精确的坐标变换.所以式(14)和式(15)所得的特征值和特征向量是简支箱梁动力特性的精确解.
3 模态的剪力滞系数由式(8)和(15)可知,箱形简支梁的模态为
| $ {{\bar W}_j} = {W_j}, {{\bar U}_j} = {q_{jj}}{W_j}', $ | (16) |
则第j阶模态翼板中的正应力为
| $ {\sigma _{ij}}\left( x \right) = E{h_i}\left[{\bar W'{'_j} + \left( {1-\frac{{{y^3}}}{{{b^3}}}} \right)\bar U{'_j}} \right], $ | (17) |
式(16)模态位移下,箱梁任意截面的弯矩为
| $ {M_j}\left( x \right) =- \left[{EI\bar W'{'_j}\left( x \right) + \frac{3}{4}E{I_s}\bar U{'_j}\left( x \right)} \right]. $ | (18) |
在式(18)弯矩作用下,按欧拉梁理论所得翼板的正应力为
| $ {{\bar \sigma }_{ij}}\left( x \right) =- \frac{{M\left( x \right){h_i}}}{I} = E{h_i}\left[{\bar W'{'_j}\left( x \right) + \frac{3}{4}\frac{{{I_s}}}{I}\bar U{'_j}\left( x \right)} \right]. $ | (19) |
根据剪力滞系数的定义:
| $ {\gamma _j}\left( x \right) = \frac{{{\lambda _j} + \left( {1-\frac{{{y^3}}}{{{b^3}}}} \right)\frac{{4I}}{{3{I_s}}}\left( {{{\bar \lambda }_j}-{\lambda _j}} \right)}}{{{{\bar \lambda }_j}}}. $ | (20) |
由式(20)可知,对简支梁而言,剪力滞系数和x无关,即纵向各截面的剪力系数相同.箱梁翼板和腹板交角处的剪力滞系数为
| $ \gamma _j^e = \frac{{{\lambda _j}}}{{{{\bar \lambda }_j}}}. $ | (21) |
箱梁翼板和腹板交角处的剪力滞系数为最大剪力滞系数.最大剪力滞系数用于度量箱梁剪力滞影响的大小.式(21)表明单箱单室截面翼板和腹板交角处的剪力滞系数等于欧拉梁特征值和剪力滞影响下箱梁特征值的比.这表明对于箱梁自由振动而言,最大剪力滞系数既反映了箱梁剪力滞的大小,又反映了由于剪力滞引起梁自振频率的变化.最大剪力滞系数越大,梁的自振频率降低越多.
4 计算精度分析式(14)所得的特征值和特征向量是在忽略剪切变形和转动惯量影响后所得的精确解.为验证本文方法计算结果的精度,下面对箱型截面梁分别进行欧拉梁理论,本文方法和有限元方法的自由振动计算.其中有限元方法是采用壳单元的分析结果.箱梁截面的材料参数为:E=35 GPa,G=15 GPa.箱梁截面形式和坐标如图(1)所示,各部位的尺寸为:t=0.25 m,b=3.55 m,h=2 m.当Is/I=0.88时,腹板宽度为tw=0.4 m;当Is/I=0.94时,腹板宽度为tw=0.2 m,同时选取梁的跨度为40、30和20 m.不同方法所得箱梁的前三阶的自振频率见表 1.
| 表 1 简支薄壁箱梁的固有频率 Table 1 Natural frequencies of simply-supported thin-walled box girder |
由计算结果可知本文的方法由于忽略了转动惯量、剪切变形以及翼缘板振动的影响而与有限元结果有一定差别,但是误差并不大,可满足工程需要.同时,本文方法所得各阶模态的频率都小于欧拉梁的频率,且模态阶数越高,两者的频率相差越大,这表明剪力滞对梁的自由振动有显著影响.
5 参数分析以跨宽比(l/2b)和翼板相对转动惯量(Is/I)为参数讨论箱梁自由振动时,模态剪力滞系数和梁自振频率的变化规律.参数分析时箱梁截面的跨度和腹板厚度为变量,其余参数同前.
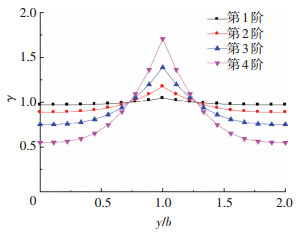
5.1 模态剪力滞系数的横向分布箱梁顶板的剪力滞分布沿箱梁中轴线左右对称,因此只画出一半的剪力滞系数.取梁的跨度为40 m,前4阶模态箱梁上翼板的剪力滞系数见图 2.
|
图 2 上翼板剪力滞系数 Figure 2 Shear lag coefficient of top flange plate |
由计算结果可知:1)腹板附近剪力滞系数最大,且γje≥1,这表明简支梁自由振动时,梁的剪力滞效应为正剪力滞效应.事实上,由式(13)可知,剪力滞使梁的特征值降低,因此,γje≥1是剪力滞使梁振动频率降低的必然结果;2)前四阶模态的最大剪力滞系数分别为1.045、1.176、1.389和1.706.这表明随着振动阶数的增加,剪力滞后效应越来越明显.剪力滞使箱梁前四阶模态的频率分别降低了2.2%、7.8%、15.1%和23.4%.因此,对于有高阶模态参与振动的箱梁,必须考虑剪力滞效应的影响.
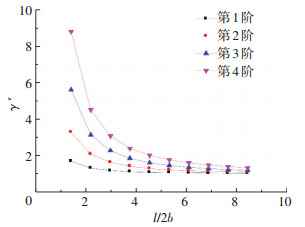
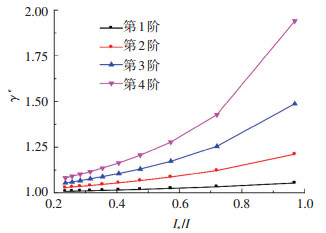
5.2 不同参数对最大剪力滞系数的影响简支梁的最大剪力滞系数随l/2b和Is/I的变化曲线见图 3、4.
|
图 3 最大剪力滞系数γe与跨宽比(l/2b)的关系 Figure 3 Relationship between γe and l/2b |
|
图 4 最大剪力滞系数γe与(Is/I)的关系(l=40 m) Figure 4 Relationship between γe and Is/I (l=40 m) |
由图可知:1)l/2b越大,γe越小.因此相同截面情况下,梁跨度越大,剪力滞影响越小.对于第一阶模态,当l/2b >4时,γe < 1.05.因此,对于仅需考虑第一阶模态振动的箱梁可忽略剪力滞效应的影响;2)Is/I反映翼缘板刚度占总刚度的百分比.Is/I显著地影响箱梁的剪力滞后效应,由此也显著影响箱梁自振频率.Is/I越大,γe越大.这说明Is/I比值越大,频率降低越多.但是,对于第一阶模态而言,Is/I < 0.9时,γe < 1.05,此时剪力滞影响很小,可以忽略不计.但是对于2阶以上模态,当Is/I >0.4时,则γe>1.05,此时,剪力滞影响不可忽略.
6 结论本文基于欧拉梁的特征值和模态,利用模态摄动法将箱梁的自由振动方程组转化为非线性代数方程组来求解,从而简化计算.应用于等截面简支梁时,可得到箱梁主频率和模态的精确解.基于箱型梁的模态,进一步推导了模态剪力滞系数.由理论分析和数值计算可得如下结论:
1) 对于简支梁而言,模态剪力滞系数沿梁轴线方向不变.且单箱单室截面翼板和腹板交角处的剪力滞系数等于欧拉梁特征值和剪力滞影响下箱梁特征值的比.
2) 腹板附近剪力滞系数最大,且γje≥1,这表明简支箱梁自由振动时,梁的剪力滞效应为正剪力滞效应.
3) 随着模态阶数的增加,剪力滞效应越来越大,由此导致箱梁高阶模态的自振频率显著降低.
4) l/2b越小,Is/I越大,γe越大.当l/2b >4或Is/I < 0.9时,γe < 1.05.此时,对于仅需考虑第一阶模态振动的箱梁可忽略剪力滞效应的影响.除此以外,剪力滞效应对结构动力反应的影响不可忽略,因此,一旦激振荷载能激起箱梁高阶模态的振动,剪力滞效应将显著地影响结构的动力反应.
| [1] | CHEN Jun, SHEN Shuilong, YIN Zhenyu, et al. Closed-form solution for shear lag with derived flange deformation function[J]. Journal of Constructional Steel Research, 2014, 102 (11) : 104-110. |
| [2] | GARA F, LEONI G, DEZI L. A beam finite element including shear lag effect for the time-dependent analysis of steel-concrete composite decks[J]. Engineering Structures, 2009, 31 (8) : 1888-1902. DOI: 10.1016/j.engstruct.2009.03.017 |
| [3] |
郭健, 孙炳楠. 型钢-混凝土箱形桥塔的剪力滞后效应分析[J].
哈尔滨工业大学学报, 2003, 35 (s) : 269-271, 275.
GUO Jian, SUN Bingnan. Analysis of shear lag effect of steel-concrete composite box tower in cable-stayed bridge[J]. Journal of Harbin Institute of Technology, 2003, 35 (s) : 269-271, 275. |
| [4] |
王浩, 李爱群, 赵大亮, 等. 润扬悬索桥钢箱梁受力分析及实验研究[J].
哈尔滨工业大学学报, 2006, 38 (7) : 1062-1064.
WANG Hao, LI Aiqun, ZHAO Daliang, et al. FE analysis and experimental study on local stress of steel box girder of runyang suspension bridge[J]. Journal of Harbin Institute of Technology, 2006, 38 (7) : 1062-1064. |
| [5] | ZHANG Yuanhai, LIN Lixia. Shear lag analysis of thin-walled box girders based on a new generalized displacement[J]. Engineering Structures, 2014, 61 (1) : 73-83. |
| [6] |
甘亚南, 吴亚平, 王根会, 等. 剪力滞效应对简支箱梁自振特性的影响研究[J].
兰州铁道学院学报, 2002, 21 (3) : 23-25.
GAN Y N, WU Y P, WANG G H, et al. Influence of shear lag on the characteristic of free vibration to box girder under simply supported[J]. Journal of Lanzhou Railway Institute, 2002, 21 (3) : 23-25. |
| [7] |
吴有俊, 罗旗帜, 陈玉骥. 考虑剪力滞效应简支箱梁自振方程的求解[J].
佛山科学技术学院学报(自然科学版), 2010, 28 (2) : 12-17.
WU Youjun, LUO Qizhi, CHEN Yuji. The Solution of free vibration equation to simply-supported box girder considering shear lag effect[J]. Journal of Foshan University (Natural Science Edition), 2010, 28 (2) : 12-17. |
| [8] |
张永健, 黄平明. 一种计入剪力滞及剪切变形效应的箱梁自振频率计算方法[J].
郑州大学学报(工学版), 2007, 28 (1) : 51-55.
ZHANG Yongjian, HUANG Pingming. A new method to calculate the natural frequencies of simply supported box girder including the effect of shear lag and shear deformation[J]. Journal of Zhengzhou University (Engineering Science), 2007, 28 (1) : 51-55. |
| [9] |
甘亚南, 周广春, 赫中营. 大悬臂板矩形截面箱梁动力反应的分析[J].
振动与冲击, 2010, 29 (11) : 61-65.
GAN Y N, ZHOU G C, HE Zhongying. Dynamic response analysis for a large cantilever rectangular box girder in consideration of shear lag effect[J]. Journal of Vibration & Shock, 2010, 29 (11) : 61-65. |
| [10] |
甘亚南, 周广春. 基于能量变分原理的薄壁箱梁自振特性分析[J].
中国公路学报, 2007, 20 (1) : 73-78.
GAN Yanan, ZHOU Guangchun. Analysis of free vibration characteristics of thin-walled box girder based on energy variation principle[J]. China Journal of Highway & Transport, 2007, 20 (1) : 73-78. |
| [11] | ZHOU Wangbao, JIANG Lizhong, YU Zhiwu. Analysis of free vibration characteristic of steel-concrete composite box-girder considering shear lag and slip[J]. Journal of Central South University, 2013, 20 : 2570-2577. DOI: 10.1007/s11771-013-1770-x |
| [12] |
楼梦麟. 变参数土层的动力特性和地震反应分析[J].
同济大学学报, 1997, 25 (2) : 155-160.
LOU Menglin. Dynamic analysis for modal characteristics and seismic response of soil layer with variable properties[J]. Journal of Tongji University, 1997, 25 (2) : 155-160. |
| [13] |
楼梦麟, 吴京宁. 复杂梁动力问题的近似分析方法[J].
上海力学, 1997, 18 (3) : 234-240.
LOU Menglin, WU Jingning. An approach to approximate analysis of dynamic problems of complicated beams[J]. Shanghai Journal of Mechanics, 1997, 18 (3) : 234-240. |
| [14] |
张怀静, 潘旦光. 变截面连续梁动力特性的半解析解法[J].
北京科技大学学报, 2008, 30 (6) : 590-593.
ZHANG Huaijing, PAN Danguang. Semi-analytic solution to dynamic characteristics of non-uniform continuous beams[J]. Journal of University of Science and Technology Beijing, 2008, 30 (6) : 590-593. |
| [15] |
潘旦光, 楼梦麟. 变截面Timoshenko简支梁动力特性的半解析解[J].
工程力学, 2009, 26 (8) : 6-9.
PAN D G, LOU M L. Semi-analytic solution of dynamic characteristics of non-prismatic timoshenko simply supported beams[J]. Engineering Mechanics, 2009, 26 (8) : 6-9. |
| [16] | PAN Danguang, CHEN Genda, LOU Menglin. A modified modal perturbation method for vibration characteristics of non-prismatic Timoshenko beams[J]. Structural Engineering and Mechanics An international Journal, 2011, 40 (5) : 689-703. DOI: 10.12989/sem.2011.40.5.689 |
 2016, Vol. 48
2016, Vol. 48


