2. 北京工业大学 建筑工程学院,北京 100124
2. College of Architecture Civil Engineering, Beijing University of Technology, Beijing 100124, China
材料在使用过程中,与周边环境介质间发生化学或电化学作用而导致的破坏或变质现象称为腐蚀[1].腐蚀会导致材料的性能下降乃至失效.探讨钢材腐蚀后的材料性能退化规律,研究在役钢结构构件腐蚀后的受力性能是进行在役钢结构安全评估的基础,具有重要理论意义和工程应用价值.
点蚀是一种局部和剧烈的腐蚀形态,经常在突然之间导致事故,因而在各种腐蚀形态中尤为有害.对于点蚀机理及点蚀生长模型,国内外学者已进行了一些研究,为点蚀构件力学性能评估的参数选取提供了一定依据.Caleyo等[2]采用Monte Carlo方法研究埋地管道外壁蚀孔深度和蚀孔生长速率的概率分布,分析了蚀孔生长的变化规律,认为最大蚀孔深度和暴露时间符合幂函数关系;Melchers[3-4]按照传统观念,将点蚀最大孔深处理成极值分布,提出了低碳钢在海洋浸水环境下点蚀最大孔深概率分布模型和点蚀孔深生长五阶段模型,并以管道实例说明了考虑点蚀影响的结构可靠性分析流程;Rybalka等[5]研究了403钢表面蚀孔发展规律,发现初期蚀孔直径和深度均增长,后期几乎只在深度方向上增长;王燕舞[6]研究了实船构件的蚀孔形态、点蚀深度统计规律、蚀孔最大深度时变模型和蚀孔径深比时变模型,构成了完整的船舶结构钢点蚀多参数概念模型,该模型还有待与更翔实的数据相验证.点蚀生长规律与材料种类、环境特性有关,目前学术界对点蚀的形成和扩散机制还存在很大争议,迄今没有比较有说服力的点蚀生长模型.
在点蚀构件力学性能分析方面,目前的研究多集中于点蚀构件的力学性能评价,方法多为根据有限元分析及试验数据拟合得到经验公式,涉及点蚀特性的各种参数.江晓俐等[7-8]进行了在面内压力作用下点蚀低碳钢板的非线性有限元分析,指出在众多影响因素中,点蚀密集度指标和单侧点蚀引起的偏心对钢板的极限抗压能力有显著影响,但未给出量化的极限强度评估公式;Duo等[9]对256个具有各种点蚀分布及尺寸的方板进行了非线性有限元计算,系统地分析多个因素对极限强度的影响,得到了预测局部腐蚀非加筋板的极限强度经验公式,但其分析只是针对腐蚀在板边区域的情况,而未考虑腐蚀发生在其它位置的情况;Sharifi等[10]基于人工神经网络技术,研究了不同点蚀深度、直径和数目的钢板极限承载力与体积损失率之间的关系,但点蚀孔参数的选取并无试验依据;Lee等[11]以电腐蚀和氯化物腐蚀方法分别制作均匀腐蚀和点蚀钢筋构件,对均匀腐蚀和点蚀构件的屈服强度、抗拉强度、弹性模型和伸长率进行了试验研究和数值模拟,提出了钢筋力学性能随锈蚀率变化的拟合计算公式,该结论推广到钢管、钢板等构件的适用性存疑.
本文结合人工加速腐蚀试验数据,以锈蚀率和最大点蚀深度为基础,对点蚀孔深度、直径及分布作出适当假定,并考虑涂层寿命的影响,以锈蚀率相等为原则建立试验室和自然大气条件下腐蚀程度的转换关系,确定不同大气暴露时间下点蚀构件的等效弹性模量,提出自然环境下点蚀构件力学性能分析的实用计算方法.
1 人工加速腐蚀试验自然环境下的暴露试验是一种接近使用环境的较可靠的腐蚀试验方法,但由于试验周期长,速度慢,耗费大量的人力与物力,且试验区域性很强,不利于试验结果的推广和应用.近年来加速腐蚀试验越来越受到重视,它能在短时间内较快地得到试验结果,并且通过短时间的加速试验可在一定程度上推测材料长期腐蚀行为的可能性,可分析研究某一个或几个典型的环境因素对材料腐蚀的影响及其作用规律.带有干燥过程并周期性盐水喷雾的盐雾复合试验方法可较好地模拟和加速大气腐蚀,能较为真实地再现自然环境,接近材料在自然大气环境中的腐蚀情况.
文献[12]以无涂层Q235钢为研究对象,进行周期喷雾复合腐蚀试验.试件尺寸为280 mm×50 mm×8 mm的钢板,试件分为9组,每组3块,每个试件用环氧包裹一定宽度.试验采用YWX/Q-020型盐雾箱,采用质量百分比为5%的氯化钠测试溶液,每次连续喷6 h,停喷6 h,12 h为一个周期.每进行14 d取出一组试件,得到腐蚀试样,将试样浸入体积比为12%的盐酸溶液中30分钟,用钢刷清洗表面腐蚀产物,再用氢氧化钠溶液中和,继而用水冲洗干净,取出后放在干燥箱中烘干并称重.
试验采用PS50三维非接触式表面形貌仪采集试样表面腐蚀数据,取环氧包裹的试件表面作为测量时试件表面腐蚀深度的基准面,即可得到腐蚀深度的绝对值.该试验锈蚀率结果见表 1.
| 表 1 人工加速腐蚀试验锈蚀率 Table 1 Corrosion rates of artificial accelerated corrosion test |
一般认为钢大气腐蚀中锈蚀率的发展遵循幂函数规律,以幂函数ηs=2.320t0.537(ηs为锈蚀率,%;t为腐蚀时间,周)拟合表 1中数据,拟合公式的相关系数R2=0.959,可知该组数据以幂函数拟合效果较好,一定程度上证明了该组数据的可靠性.
大量的试验数据和理论证明,局部腐蚀最大蚀孔深度服从Gumbel分布函数.文献[12]对上述试验不同腐蚀时间的试件点蚀深度进行了统计,发现点蚀深度符合Gumbel极值分布,取保证率为95%,计算最大点蚀深度,见表 2.
| 表 2 腐蚀深度检验结果 Table 2 Inspection results of corrosion depth |
进行均匀腐蚀锈蚀构件强度计算通常直接扣除因腐蚀损失的板厚,而建立一个全面合理的点蚀模型,蚀孔形状、最大点蚀深度、平均点蚀深度、蚀孔径深比、单位面积蚀孔数目及分布情况均是重要指标.采用有限单元法评定考虑点蚀影响的结构构件力学性能,首要任务就是依据构件的实际受腐蚀情况,合理选用点蚀孔的几何形态及沿板面的分布情况.
一般而言,长方体、圆柱体、球冠体、半球体、圆锥体等是点蚀孔最常取的形状,这种差异主要由腐蚀环境、金属材料以及模型易用性的不同引起的.考虑到点蚀孔几何形态的简洁性,本文取蚀孔形状为圆柱体.
点蚀引起的构件力学性能下降,主要原因在于净截面损失,因此最大点蚀深度往往比平均点蚀深度影响更大.点蚀孔的直径可小可大,但大多数情况下都比较小.一般蚀孔可以描述为表面直径等于或者小于深度的洞穴[1].王艳舞[6]得出结论:不同长宽比与不同蚀孔深度的条件下,极限强度均随蚀孔径深比的增大而下降.因此在研究点蚀构件力学性能时,取径深比为1,即蚀孔深度与直径相等是偏于安全的.
综上所述,考虑到腐蚀情况的复杂性,作出如下基本假定:1)构件只发生点蚀,蚀孔形状为圆柱体;2)各个蚀孔深度相同,均取最大点蚀深度;3)蚀孔径深比为1,即蚀孔深度与直径相等;4)蚀孔在构件上均匀分布.
文献[12]试验中试件为钢板,锈蚀发生于钢板两侧,表 1中锈蚀率为试件双侧锈蚀产生的质量损失率.为计算构件单侧的锈蚀深度,此处锈蚀体积取构件单侧锈蚀所损失的金属体积,因而得到
| $ V = \frac{{{m_0}{\eta _{\rm{s}}}}}{{2\rho }} = \frac{{{V_0}\rho {\eta _{\rm{s}}}}}{{2\rho }} = \frac{{{V_0}{\eta _{\rm{s}}}}}{2}. $ | (1) |
式中:V为构件单侧锈蚀所损失的金属体积,m0为腐蚀前的试件质量,ηs为锈蚀率,V0为锈蚀前的试件体积,ρ为试件的密度.
最大蚀孔深度由表 2得到.根据基本假定,蚀孔直径与最大蚀孔深度相同,则单位面积蚀孔数目由锈蚀体积、蚀孔深度、蚀孔直径、钢板面积计算得到,即
| $ n = \frac{N}{S} = \frac{V}{{{V_1}S}} = \frac{V}{{{D_m} \cdot {\rm{\pi }}{{\left( {\frac{d}{2}} \right)}^2}S}} = \frac{{4V}}{{{\rm{\pi }}S{D_m}{d^2}}}. $ | (2) |
式中:n为单位面积蚀孔数目,N为蚀孔总数,S为钢板面积,V为锈蚀体积,由式(1)得到,V1为单个蚀孔体积,Dm为最大蚀孔深度,d为蚀孔直径.
综上,得到不同锈蚀时间构件的腐蚀状态见表 3.
| 表 3 不同锈蚀时间下的蚀孔状态 Table 3 States of corrosion holes at different time |
目前国内外钢结构工程主要采用防腐涂层减轻或防止钢结构的锈蚀,钢结构的腐蚀发生在其表面防腐涂层失效之后,因此在分析钢结构的腐蚀退化规律时,涂层的影响不可忽略.钢结构防腐涂层的失效是一个经年变化的长期过程,包含诸多复杂和随机的因素,因而目前并无具有普适性的研究成果.
国家体育场“鸟巢”的设计提出了25 a的长效防腐要求,并对其在防腐年限内的耐久性提出明确指标,然而25 a后“鸟巢”的防腐涂层系统的耐久性仍不得而知.秦国治等[13]指出在已投入使用十多年的情况下,茂名石化公司炼油厂35#汽油罐的涂层表现良好.基于此,花晶晶[14]提出,可偏于安全地取防腐涂层寿命为10 a.
自然大气条件下,试件上由雨、雾等形成的液膜有一个由厚到薄、由湿到干的周期性循环过程,前文已述,文献[12]能较为真实地再现自然环境.当然作为一种人工加速腐蚀试验方法,其与海洋大气环境并不能严格的对应,但考虑到模型的易用性,本文采用锈蚀率相等的原则进行换算.
梁彩凤等[15]给出了青岛地区8 mm厚的Q235钢板16年的锈蚀率数据,见表 4.
| 表 4 青岛地区Q235钢16 a锈蚀率数据 Table 4 Corrosion rate data of Q235 steel in Qingdao |
根据最小二乘法得到青岛地区Q235钢锈蚀率和时间的拟合函数关系为ηs=1.423t0.6,拟合公式的相关系数R2=0.984.考虑涂层寿命的影响,则本文认为锈蚀率随时间的增长模型为
| $ \left\{ \begin{array}{l} {\eta _{\rm{s}}} = 0, 0 \le t \le 10;\\ {\eta _{\rm{s}}} = 1.423{\left( {t-10} \right)^{0.6}}, t > 10. \end{array} \right. $ | (3) |
式中:ηs为锈蚀率,%;t为时间,a.
本文采用锈蚀率相等的原则进行换算,则有人工加速腐蚀试验环境和海洋大气环境下时间对应关系见表 5.
| 表 5 人工加速腐蚀试验环境和海洋大气环境下时间对照关系 Table 5 Time comparison relationship between artificial accelerated corrosion test and marine atmosphere environment |
本文研究对象取为钢管,外表面发生点蚀,两端受轴向均布压力,采用ANSYS有限元软件计算构件沿长度方向的变形,继而计算构件的等效材料性能.定义等效弹性模量为
| $ {E_{\rm{c}}} = \frac{{PL}}{{\Delta L}}. $ | (4) |
式中:Ec为等效弹性模量,P为模型构件两端施加的均布压力,L为构件几何长度,ΔL为构件沿长度方向的变形.
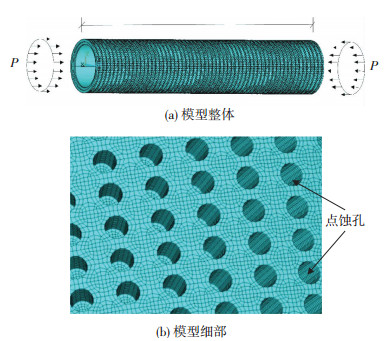
模型见图 1,端部均布压力P大小为100 MPa,构件几何长度L取0.25 m (计算结果与端部力大小和构件几何长度无关).模型横截面取外径为63.5 mm,壁厚为4 mm.蚀孔在钢管外表面均匀分布.单元类型选用SOLID95单元.
|
图 1 点蚀钢管有限元模型(获取等效弹性模量) Figure 1 The finite model of a pitting steel pipe |
根据表 3和表 5,确定不同大气暴露时间下的孔蚀参数,即蚀孔深度、蚀孔直径、单位面积蚀孔数目,根据图 1有限元模型,依据式(4)得到等效弹性模量Ec,结果见表 6.
| 表 6 自然大气环境不同暴露时间下点蚀钢管等效弹性模量 Table 6 The equivalent elastic modulus of pitting steel pipe at different atmospheric corrosion exposure time |
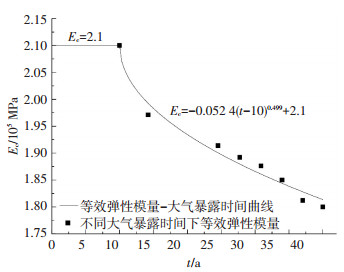
由表 6可知,在涂层失效之后,随着大气暴露时间的增长,点蚀钢管的等效弹性模量逐渐减小.用幂函数拟合表 6涂层失效后等效弹性模量与大气暴露时间之间的关系,即
| $ \left\{ \begin{array}{l} {E_{\rm{c}}} = 2.1, 0 \le t \le 10;\\ {E_{\rm{c}}} =-0.0524{\left( {t-10} \right)^{0.499}} + 2.1, t > 10. \end{array} \right. $ | (5) |
式中:Ec为等效弹性模量,105 MPa;t含义同式(3).幂函数拟合公式的相关系数R2=0.914.
等效弹性模量-大气暴露时间曲线见图 2.
|
图 2 等效弹性模量-大气暴露时间关系 Figure 2 The relationship between equivalent elastic modulus and atmospheric corrosion exposure time |
为验证上述方法所得等效弹性模量Ec的合理性,取一端固支的悬臂圆管,几何尺寸与前文相同,建立3个模型:
1) 未腐蚀构件,弹性模量为E=2.1×105 MPa;
2) 海洋大气环境暴露时间为33.97 a的点蚀构件,按照本文第2节基本假定将点蚀孔逐一建立在模型中,见图 1;
3) 等效点蚀构件,即截面尺寸与图 1(a)相同,弹性模量取式(5)计算得到的大气暴露时间33.97 a对应的的等效弹性模量Ec=1.845×105 MPa.
三者在均布线荷载10 kN/m作用下的变形见图 3.由计算可知,未腐蚀构件自由端挠度为0.070 mm,点蚀构件自由端挠度为0.077 mm,等效点蚀构件自由端挠度为0.078 mm.点蚀构件与等效点蚀构件自由端挠度几乎相等,验证了本文提出的采用等效弹性模量分析腐蚀构件受力性能方法的正确性.

|
图 3 悬臂构件均布荷载下变形 Figure 3 The deformation of cantilever member under uniform load |
对于均匀腐蚀,构件全长度范围内截面损失相同,依据式(4)所定义的等效弹性模量,均匀腐蚀构件的等效弹性模量可直接取:
| $ {E_c}' = \left( {1-{\eta _{\rm{s}}}} \right)E. $ | (6) |
式中:E′c为均匀腐蚀条件的等效弹性模量;E为原始弹性模量,取为2.1×105 MPa;ηs含义同式(3).
为比较点蚀与均匀腐蚀对构件等效弹性模量的不同影响,表 7列出了相同锈蚀率条件下两种腐蚀状态等效弹性模量的数值.由表 7可知,相同锈蚀率条件下,依据点蚀计算得到的等效弹性模量小于依据均匀腐蚀计算得到的等效弹性模量,两者的比值在96.9%~98.3%,原因在于相同锈蚀率条件下点蚀比均匀腐蚀对构件局部截面的削弱更为严重.
| 表 7 相同锈蚀率下均匀腐蚀和点蚀构件等效弹性模量 Table 7 The equivalent elastic modulus of pitting corrosion members and uniform corrosion members with the same corrosion rate |
1) 以锈蚀率相等为原则,并考虑涂层寿命的影响,建立了试验室和海洋大气条件下锈蚀构件力学性能参数的转换关系.
2) 根据弹性模量的基本力学概念,确定了不同大气环境暴露时间下点蚀构件的等效弹性模量,得到了自然大气环境下点蚀钢构件等效弹性模量实用计算公式.
3) 在相同锈蚀率条件下,点蚀构件的等效弹性模量低于均匀腐蚀构件.
4) 本文目的是提供一种能够评价腐蚀后构件力学性能劣化的简化方法的研究思路.作为一种人工加速腐蚀试验方法,其与海洋大气环境并不能严格的对应,更无法与自然大气环境严格对应(本文未检索到自然大气环境下的腐蚀数据),但考虑到模型的易用性,本文采用锈蚀率相等的原则进行换算,以提出简化方法.特请读者注意.
| [1] |
FONTANA M G, GREENE N D.腐蚀工程[M].左景尹, 译.北京:化学工业出版社, 1982:63-65.
FONTANA M G, GREENE N D. Corrosion engineering[M]. ZUO J Y (Translated). Beijing: Chemical Industry Press, 1982: 63-65. |
| [2] | CALEYO F, VELáZQUEZ J C, VALOR A. Probability distribution of pitting corrosion depth and rate in underground pipelines: A Monte Carlo study[J]. Corrosion Science, 2009, 51 (9) : 1925-1934. |
| [3] | MELCHERS R E. Pitting corrosion of mild steel in marine immersion environment-part l:maximum pit depth[J]. Corrosion, 2004, 60 (9) : 824-836. DOI: 10.5006/1.3287863 |
| [4] | MELCHERSR E. Representation of uncertainty in maximum depth of marine corrosion pits[J]. Structural Safety, 2005, 27 : 322-334. DOI: 10.1016/j.strusafe.2005.02.002 |
| [5] | RYBALKA K V, SHALDAEV V S, BEKETAEVA L A. Development of pitting corrosion of stainless steel 403 in sodium chloride solutions[J]. Russian Journal of Electrochemistry, 2010, 46 (2) : 196-204. DOI: 10.1134/S1023193510020114 |
| [6] |
王燕舞.考虑腐蚀影响船舶结构极限强度研究[D].上海:上海交通大学, 2008:80-89.
WANG Y W. Ultimate strength of ship structures with corrosion wastage[D]. Shanghai: Shanghai Jiao Tong University, 2008: 80-89. |
| [7] | JIANG X L, SOARES C. Nonlinear FEM analysis of pitted mild steel square plate subjected to in-plane compression[J]. Journal of Ship Mechanics, 2009, 13 (3) : 398-405. |
| [8] |
江晓俐, 吴卫国, 梁志勇. 点腐蚀作用下非穿透低碳钢板的极限抗压承载能力数值分析[J].
武汉理工大学学报(交通科学与工程版), 2009, 33 : 1167-1170.
JIANG X L, WU W G, LIANG Z Y. Ultimate Compressive Capacity Analysis of Pitted Non-through Mild Steel Plates[J]. Journal of Wuhan University of Technology (Transportation Science & Engineering), 2009, 33 : 1167-1170. |
| [9] | DUO O K, PU Y C, INCECIK A. Computation of ultimate strength of locally corroded unstiffened plates under uniaxial compression[J]. Marine Structures, 2007, 20 : 100-114. DOI: 10.1016/j.marstruc.2007.02.003 |
| [10] | SHARIFI Y, TOHIDI S. Ultimate capacity assessment of web plate beams with pitting corrosion subjected to patch loading by artificial neural networks[J]. Advanced Steel Construction, 2014, 10 (3) : 325-350. |
| [11] | LEE H S, CHO Y S. Evaluation of the mechanical properties of steel reinforcement embedded in concrete specimen as a function of the degree of reinforcement corrosion[J]. International Journal of Fracture, 2009, 157 (1) : 81-88. |
| [12] |
薛南, 徐善华, 史斌. Q235钢表面腐蚀深度的统计规律研究[J].
四川建材, 2013, 39 : 117-118.
XUE N, XU S H, SHI B. Statistical research on the surface corrosion depth of Q235 steel[J]. Sichuan Building Materials, 2013, 39 : 117-118. |
| [13] |
秦国治, 王顺. 富锌涂料综述[J].
石油和化工设备, 2001 (5) : 55-58.
QIN G Z, WANG S. Review of Zinc-rich paint[J]. Oil and Chemical Equipment, 2001 (5) : 55-58. |
| [14] |
花晶晶.大跨空间网格结构参数敏感性分析与疲劳分析[D].南京:东南大学, 2012:57-72.
HUA J J. Sensitivity analysis of parameters and fatigue analysis for large-span space lattice structures[D]. Nanjing:Southeast University, 2012: 57-72. |
| [15] |
梁彩凤, 侯文泰. 碳钢、低合金钢16年大气暴露腐蚀研究[J].
中国腐蚀与防护学报, 2005, 25 (1) : 1-6.
LIANG C F, HOU W T. Sixteen-year atmospheric corrosion exposure study of steels[J]. Journal of Chinese Society for Corrosion and Protection, 2005, 25 (1) : 1-6. |
 2016, Vol. 48
2016, Vol. 48


