2. 同济大学 地下建筑与工程系, 上海 200092
2. Department of Geotechnical Engineering, College of Civil Engineering, Tongji University, Shanghai 200092, China
静压桩由于施工速度快、工期短、不受季节限制、单桩承载力高等优点,在软土地区基础工程建设中得到了广泛应用[1-6].然而,静压桩作为挤土桩,其在压入饱和粘性土地基的过程中桩身将置换相同体积的土,对桩周土体产生巨大的挤压作用,使桩周土体中产生较高的超孔隙水压力,造成桩周土体有效应力大幅度减小致使土体强度降低.沉桩结束后,沉桩产生的超孔隙水压力逐渐消散,伴随土体有效应力和强度逐渐恢复与提高,使静压桩承载力具有明显的时效性.因此,对静压桩周土体的强度变化规律展开研究,为科学合理确定静压桩时变承载力提供理论依据,具有重要的现实与科学意义.
目前,国内外学者对饱和粘土中静压桩周土体力学特征的变化开展了相关研究:Bishop等[7]基于大量的饱和土不排水直剪试验,提出了确定饱和土体不排水抗剪强度的经验性方法;Vesic等[8]将静压沉桩过程视作柱孔扩张,基于土体各向同性假设条件下的柱孔弹塑性扩张解对静压桩周土体强度的变化进行了研究;Wroth等[9]基于弹塑性模型并引入了参数Λ建立了土体不排水抗剪强度理论,并且推导出了初始应力各向异性的正常固结土在平面应变条件下的不排水抗剪强度公式;Randolph等[10-11]基于柱孔扩张理论,采用修正剑桥模型推导了沉桩扩孔问题的弹塑性解析解,探究了静压沉桩效应对桩周土体力学特性的影响;Ohta[12]根据二维弹塑性模型,进行了土体不排水抗剪强度公式的推导,并且提出正常固结土的不排水抗剪强度的各向异性主要受应力诱发各向异性的影响;张冬梅等[13]基于恒定剪切速率的室内试验对不同应力历史的天然软黏土的不排水抗剪强度时效特性进行了研究;宰金珉等[14]引入时间、深度参数,分析了饱和软土中静压桩沉桩引起的超孔隙水压力,推导出了超孔隙水压力与其消散的准三维解答.
从上述研究可发现,在饱和粘土中柱孔不排水扩张的问题上,Randolph等[10-11]虽然基于修正剑桥模型推导并给出了柱孔不排水扩张后桩周土体应力场的解析表达式,但其在解答过程中没有考虑到土体初始各向异性与应力历史所带来的影响,使得解答无法较为完整地反映桩周土体强度的时变机理.本文在上述学者研究的基础上,从临界状态土力学概念出发,考虑K0固结天然黏土的初始应力各向异性及加载过程中应力诱发各向异性特征,首先推导出静压桩沉桩过程中桩周土体的应力解答.在此基础上,基于轴对称固结理论推导出静压桩桩周土体的固结控制方程,并考虑桩周土体固结过程中的松弛效应,研究饱和粘土中静压桩周土体强度的时变规律.
1 沉桩过程解析 1.1 沉桩力学模型如图 1所示,根据饱和粘性土中静压沉桩过程桩周土体的位移形态,可将桩身的贯入过程用柱孔不排水扩张来模拟[8, 10-12].假设土体为K0固结初始应力各向异性天然饱和粘土.其初始竖向应力为σv0,水平向应力为σh0,初始孔隙水压力为u0,将沉桩过程视作初始半径为r0的柱形孔在内压力σra作用下不排水扩张,孔径最终扩张至桩半径ru,桩周土体受挤压和剪切产生超孔隙水压力Δu.桩周弹性区域内土体应力应变关系服从胡克定律,桩侧塑性区域内土体采用大变形理论和K0固结条件下的修正剑桥模型(K0-MCC)来描述其力学行为.在柱孔扩张过程中,以rp表示孔径扩张为ru时所对应的塑性区半径.

|
图 1 柱孔扩张力学模型 Figure 1 Mechanical model for expansion of cylindrical hole |
为考虑土体初始各向异性及受力过程中初始应力诱发各向异性对土体力学性能的影响,采用K0-MCC模型描述土体塑性阶段的应力应变关系.K0-MCC模型[15-17]是在剑桥模型(MCC)的基础上分别引入参数相对应力比η*和相对临界状态应力比M*,从而代替修正剑桥模型中的应力比η=q/p′和临界状态应力比M,以此来考虑各向异性对土体力学特性的影响.K0-MCC模型的屈服方程为[15]
| $ f = 1 + {\left( {\frac{{{\eta ^*}}}{{{M^*}}}} \right)^2}-\frac{{{{p'}_{\rm{c}}}}}{{p'}} = 0. $ | (1) |
式中:p′c为土体K0固结条件下的屈服应力,p′为平均有效主应力;相对应力比η*和相对临界状态应力比M*的表达式为
| $ {\eta ^*} = \sqrt {\frac{3}{2}\left( {{\eta _{ij}}-{\eta _{ij0}}} \right)\left( {{\eta _{ij}}-{\eta _{ij0}}} \right)}, $ | (2) |
| $ {M^*} = \sqrt {{M^2}-\eta _0^2} . $ | (3) |
基于K0-MCC弹塑性本构模型及相关的应力应变关系,并将其与式(1)~(3)进行联立,可以解得柱孔扩张在平面应变条件下土体达到临界状态时对应的平均有效主应力p′sf和广义偏应力qsf分别为:
| $ \frac{{{{p'}_{{\rm{sf}}}}}}{{{{p'}_0}}} = {\left( {\frac{{{\rm{OCR}}}}{2}} \right)^\mathit{\Lambda }}, $ | (4) |
| $ \frac{{{{p'}_{{\rm{sf}}}}}}{{{{p'}_0}}} = M{\left( {\frac{{{\rm{OCR}}}}{2}} \right)^\mathit{\Lambda }}. $ | (5) |
式中:M为p′-q平面内CSL线的斜率,其值为6sin φ′/(3-sin φ′),其中φ′为土体的有效内摩擦角;Λ=1-κ/λ为塑性体应变率;OCR为土体的超固结比,定义为OCR=p′c/p′0.
结合弹塑性边界条件、平衡微分方程式、K0-MCC模型的临界状态条件及各应力分量之间的关系,可解得桩周塑性区内任意位置r(x)处的竖向应力分量:
| $ {\sigma _{\rm{z}}}\left( x \right) = {\sigma _{{r_{\rm{p}}}}} + \xi {{p'}_{{\rm{sf}}}}\left\{ {\ln {c_{\rm{p}}}{{\left[{{r_{\rm{u}}}/r\left( x \right)} \right]}^2} -1} \right\} -\sqrt {q_{{\rm{sf}}}^2 -3{\xi ^2}{{p'}_{{\rm{sf}}}}^2} . $ | (6) |
式中:
| $ \xi = \sqrt {\frac{{{M^2}{{\left( {2{K_0} + 1} \right)}^2} - 9{{\left( {1 - {K_0}} \right)}^2}}}{{3{{\left( {2{K_0} + 1} \right)}^2}}}} ,$ | (7) |
| $ {c_{\rm{p}}} = \sqrt {\frac{3}{{{\rm{OCR}}-1}}} \frac{G}{{{M^*}}}. $ | (8) |
式中:M*为相对临界状态应力比;G为土体剪切模量,其值为G=3(1-2ν′)υp′/[2(1+ν′)κ],其中κ为υ-ln p′平面上卸荷曲线的斜率,υ为比体积,p′为平均有效主应力.
通过上述桩周土体应力表达式(4)~(6),并根据有效应力原理可解得桩周塑性区内任意位置处的超孔隙水压力Δur(x):
| $ \Delta {u_{r\left( x \right)}} = {{p'}_0}\left[ {\frac{{3{K_0}}}{{1 + 2{K_0}}} - {{\left( {\frac{{{\rm{OCR}}}}{2}} \right)}^\mathit{\Lambda }} + \frac{G}{{{c_{\rm{p}}}}}} \right] + \xi {{p'}_{{\rm{sf}}}}\left\{ {\frac{{{c_{\rm{p}}}}}{{{{p'}_0}}}{{\left[ {\frac{{{r_u}}}{{r\left( x \right)}}} \right]}^2} - 1} \right\} - \frac{{\sqrt {q_{{\rm{sf}}}^2 - 3{\xi ^2}{{p'}_{{\rm{sf}}}}^2} }}{3}. $ | (9) |
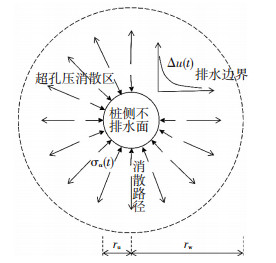
考虑到桩周土体再固结过程中,在距桩rw处孔压变化极小,故取为排水边界,即该处超孔压为0;并假设桩体不透水,即桩侧处为不排水面,如图 2所示,则沉桩结束后桩周土体固结的初始条件和边界条件为:
|
图 2 桩周土体再固结模型 Figure 2 Reconsolidation model of soil around pile |
| $ \frac{{\partial \Delta u}}{{\partial r}}\left| {_{r = {r_{\rm{u}}}}} \right. = 0, $ | (10) |
| $ \Delta u\left| {_{r = {r_{\rm{w}}}}} \right. = 0, $ | (11) |
| $ \Delta u\left| {_{r = 0}} \right. = \Delta {u_{r\left( x \right)}}, $ | (12) |
式中rw为超孔压消散影响区的半径[10],其值为rw=(5~7)rp.
2 土体强度时变效应解析 2.1 孔压消散过程解析在沉桩结束后,孔隙水压力为了在桩周达到平衡,桩侧的超孔压主要沿径向消散[10, 18],土体有效应力随之增加,强度也相应提高.假设桩周土在弹性平面应变条件下再固结,基于土体径向固结微分方程,并结合桩周土体体应变与超孔隙水压力Δu之间的关系可解得桩周土体在弹性平面应变条件下再固结的控制方程[18]为
| $ {C_{\rm{h}}}{\nabla ^2}u = \frac{{\partial u}}{{\partial t}}, $ | (13) |
式中:∇2为拉普拉斯算子,Ch为弹性平面应变条件下水平向渗透固结系数,其表达式为
| $ {C_{\rm{h}}} = \frac{{{k_{\rm{h}}}}}{{{\gamma _{\rm{w}}}}}\frac{{2\left( {1-v'} \right)G}}{{1-2v'}}, $ | (14) |
式中kh为水平的渗透系数,ν′为土体的泊松比.
由于沉桩结束后桩周超孔压主要沿径向消散,故可将固结过程中超孔压分别单独表示为时间变量t和径向坐标r的函数:
| $ \Delta u\left( {r, t} \right) = f\left( r \right)T\left( t \right). $ | (15) |
将式(19)代入式(17)并整理后可得:
| $ \frac{{{C_{\rm{h}}}}}{{f\left( r \right)}}\left[{\frac{{{\partial ^2}f\left( r \right)}}{{\partial {r^2}}} + \frac{1}{r}\frac{{\partial f\left( r \right)}}{{\partial r}}} \right] = \frac{{\partial T\left( t \right)}}{{T\left( t \right)}} = -{\mu ^2}, $ | (16) |
式中μ为一待定常数.
式(16)中时间t的函数为一阶齐次线性微分方程,r的函数为典型的0阶贝塞尔方程.求解可得式(16)通解:
| $ \Delta u\left( {r, t} \right) = f\left( r \right)T\left( t \right) = \left[{{A_{\rm{n}}}{J_0}\left( {{\chi _{\rm{n}}}r} \right) + {B_{\rm{n}}}{Y_0}\left( {{\chi _{\rm{n}}}r} \right)} \right]{e^{ -{\chi _{\rm{n}}}{C_{\rm{h}}}r}}. $ | (17) |
根据边界条件式(10)、式(11),初始条件式(12),并结合贝塞尔函数的性质可解得:
| $ {A_{\rm{n}}} = \frac{{\int_{{r_{\rm{u}}}}^{{r_{\rm{p}}}} {\Delta u\left( {r, 0} \right)G\left( {{\chi _{\rm{n}}}r} \right)r{\rm{d}}r} }}{{\int_{{r_{\rm{u}}}}^{{r_{\rm{p}}}} {G{{\left( {{\chi _{\rm{n}}}r} \right)}^2}r{\rm{d}}r} }}, $ | (18) |
| $ {B_{\rm{n}}} =-{A_{\rm{n}}}\frac{{{J_1}\left( {{\chi _{\rm{n}}}{r_{\rm{u}}}} \right)}}{{{Y_1}\left( {{\chi _{\rm{n}}}{r_{\rm{u}}}} \right)}}, $ | (19) |
| $ {J_0}\left( {{\chi _{\rm{n}}}{r_{\rm{p}}}} \right){Y_1}\left( {{\chi _{\rm{n}}}{r_{\rm{u}}}} \right)-{J_1}\left( {{\chi _{\rm{n}}}{r_{\rm{u}}}} \right){Y_0}\left( {{\chi _{\rm{n}}}{r_{\rm{p}}}} \right) = 0, $ | (20) |
| $ G\left( {{\chi _{\rm{n}}}r} \right) = {J_0}\left( {{\chi _{\rm{n}}}r} \right)-{Y_0}\left( {{\chi _{\rm{n}}}r} \right){J_0}\left( {{\chi _{\rm{n}}}{r_{\rm{w}}}} \right)/{Y_0}\left( {{\chi _{\rm{n}}}{r_{\rm{w}}}} \right). $ | (21) |
式中系数χn可通过求解式(20)得到.
2.2 桩周土体的松弛效应在沉桩过程中,由于桩体贯入对桩周土体的扰动作用,使得近桩侧的土体刚度较距桩较远处土体刚度小,在固结过程中刚度较大的土体对刚度较小的土体产生挤压效果,即远桩处土体产生回弹现象,这种现象称之为桩周土体的松弛效应.由于松弛效应的存在,使得桩侧土体总应力相应减小,故桩周土体在固结的过程中其超孔隙水压力并不能完全的转化为土体的有效应力.根据有效应力公式,并结合式(9)、(17)可得桩周土体再固结过程中任意时刻的竖向有效应力为
| $ {{\sigma '}_{\rm{v}}}\left( t \right) = \frac{{3{{p'}_{{\rm{sf}}}}}}{{2{K_0} + 1}} + \alpha \left[{\Delta {u_0}-\Delta u\left( t \right)} \right], $ | (22) |
式中α为超孔压转换系数[11],其表达式为
| $ \alpha = \frac{{{{\sigma '}_{{\rm{v0}}}}{\rm{OCR}}}}{{\mu \Delta {u_{\max }}}}\ln \left( {1 + \frac{\eta }{{{\rm{OCR}}}}\frac{{\Delta {u_{\max }}}}{{{{\sigma '}_{{\rm{v0}}}}}}} \right), $ | (23) |
式中η为一待定常数.
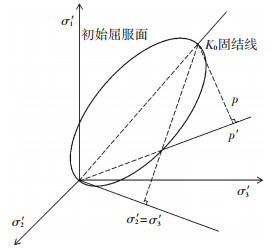
2.3 桩周土体强度的时变效应解答在计算桩周土体强度时,文献[12, 19]为了考虑土体初始各向异性及诱发各向异性,采用K0固结诱发各向异性的屈服面方程式(1),其初始屈服面为一个旋转的椭圆,如图 3所示.将沉桩结束后桩周土体的平面应变条件代入屈服函数式(1),并对两边求导可得:
|
图 3 初始屈服面 Figure 3 Initial yield surface |
| $ \frac{1}{{{{p'}_{\rm{0}}}}} + \frac{{2{\eta ^*}{M^2}}}{{\left( {{M^2} + {\eta ^*}^2} \right)}}\frac{{\partial {\eta ^*}}}{{\partial p'}} = 0. $ | (24) |
又由式(2)可得:
| $ \frac{{\partial {\eta ^*}}}{{\partial p'}} = \frac{3}{{2{\eta ^*}}}\left( {\frac{{{\eta _{ij0}}}}{{{{p'}_{\rm{0}}}}}-\frac{{{\eta _{ij}}}}{{p'}}} \right)\frac{{{\eta _{ij}}}}{{p'}}. $ | (25) |
将式(25)代入式(24)中得:
| $ \left( {\frac{{{\eta _{ij}}}}{{p'}}-\frac{{{\eta _{ij0}}}}{{{{p'}_{\rm{0}}}}}} \right)\frac{{{\eta _{ij}}}}{{p'}} = \frac{{{M^2} + {\eta ^2}}}{3}. $ | (26) |
将土体的应力条件代入上式,并结合式(2)可得土体的破坏条件为
| $ \frac{{p'}}{q} = \frac{1}{{\sqrt {{M^2} + \eta _0^2} }}, $ | (27) |
式中η0=q0/p′0=3(1-K0)/(1+2K0).
王立忠等[20]在K0修正剑桥模型的基础上,从临界土力学的概念出发,推导出了超固结状态不排水条件下球应力与偏应力之间的关系:
| $ {\left( {\frac{{{{p'}_{\rm{0}}}}}{{p'}}} \right)^{\rm{\lambda }}}{\left( {\frac{{{M^2}}}{{{M^2} + {\eta ^{*2}}}}} \right)^{{\rm{\lambda-}}\kappa }}{n^\kappa } = 1. $ | (28) |
式中:λ为加载曲线在ν-lnp′平面上的斜率;κ为卸载曲线在ν-lnp′平面上的斜率;n为超固结系数.对于正常固结土,令式(28)中的超固结系数n=1,可以求得其不排水条件下球应力与偏应力的关系:
| $ {\left( {\frac{{{{p'}_{\rm{0}}}}}{{p'}}} \right)^{\rm{\lambda }}}{\left( {\frac{{{M^2}}}{{{M^2} + {\eta ^{*2}}}}} \right)^{{\rm{\lambda-}}\kappa }} = 1. $ | (29) |
将式(27)与式(29)联立得
| $ \frac{q}{{{{p'}_{\rm{0}}}}} = \sqrt {{M^2} + \eta _0^2} {\left( {\frac{{{M^2}}}{{{M^2} + {\eta ^{*2}}}}} \right)^\mathit{\Lambda }}, $ | (30) |
式中Λ=1-κ/λ.
又由于土体的不排水抗剪强度定义为
| $ {s_{\rm{u}}} = \frac{1}{2}q.$ | (31) |
考虑到在沉桩结束后土体应力的时效性与松弛效应,将式(17)、式(22)、式(30)与式(31)联立,并根据平均有效应力与竖向有效应力间的关系,可以将固结过程中桩周土体的不排水抗剪强度表示为
| $ \frac{{{s_{\rm{u}}}\left( t \right)}}{{{{\sigma '}_{\rm{v}}}\left( t \right)}} = \frac{{\left( {2{K_0} + 1} \right)\sqrt {{M^2} + \eta _0^2} }}{3}{\left( {\frac{{{M^2}}}{{{M^2} + {\eta ^{*2}}}}} \right)^\mathit{\Lambda }}. $ | (32) |
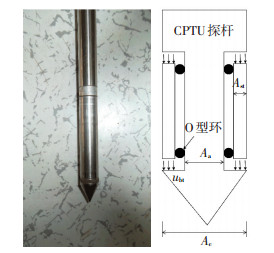
为了验证上述解答的合理性,使用同济大学TLJ-150复合型岩土离心机上开展静压桩周土体力学性能试验研究.试验的模型率为n=50 g.试验用土选取上海第⑤3-2层粉质粘土,土体重度γ=8.75 kN/m3,初始孔隙比e0=0.98,有效内摩擦角φ′=31.7°,静止侧压力系数K0=0.55,超固结比OCR=1.0.试验前根据饱和含水率配制水量并与土样进行真空搅拌,使土体成为完全饱和土,然后将土样置于模型箱中,使之在50 g的加速度下固结10 h.本次试验利用直径1 cm的孔压静力触探仪CPTU来模拟静压桩,如图 4所示,其自带的传感器可以精确的测量并记录沉桩过程中以及再固结过程中桩体的侧壁阻力、桩尖阻力和桩侧孔隙水压力的变化.
|
图 4 CPTU模型桩测试原理 Figure 4 Testing principle for CPTU model pile |
孔压静力触探仪CPTU并不能直接测得土体不排水抗剪强度,但土体的不排水抗剪强度可采用有效锥尖阻力qe表示为[21-22]
| $ {s_{\rm{u}}} = \frac{{{q_{\rm{e}}}}}{{{N_{{\rm{ke}}}}}}. $ | (33) |
式中:有效锥尖阻力qe=qt-ubt为修正锥尖阻力qt与孔压值ubt的差值,qt=qc+u′(1-a)为修正锥尖阻力,qc为测试锥尖阻力, ubt为锥肩上的孔压测试值, a为净面积比, Nke为经验圆锥系数,Senneset等[23]提出在粘土及粉质粘土条件下,Nke的取值为6~12.
由于本次试验是在1/50的缩尺离心模型中进行,根据离心试验的相似第三定律,若模型置于Ng的离心力场中,则模型中孔隙水压的消散时间是为原型的1/N2倍.为方便试验结果与理论计算结果相对比,下述所有离心机模型试验结果所对应的时间均为按模型比例尺1/N2还原为的真实时间.
图 5为桩端处土体强度变化与孔压消散曲线的对比图.从孔压消散曲线可以看出,离心机试验值与本文计算得到的理论值之间具有较好的吻合性,说明本文所采用的考虑初始各向异性的柱孔扩张力学模型能够较为准确的反应桩周土体在再固结过程中超孔隙水压力沿径向消散的状况.

|
图 5 桩端处土体强度变化与孔压消散曲线 Figure 5 Curve of soil strength variation and pore pressure dissipation at the tip of pile |
同时,从桩端处土体强度变化曲线可以看出,离心机试验值曲线与本文理论计算值的趋势基本一致.但是,由于在沉桩结束后,离心试验条件下沉桩产生的超孔隙水压力迅速消散,此时桩周土体由于沉桩挤压的扰动,土体在触变作用下其强度有所损失且在较短时间内得不到恢复,故理论计算桩周土体强度前期增长速率要略高于离心试验测试结果.
3.2 土体参数对土体强度时效性的影响从上述分析可知,沉桩结束后,桩周土体的强度变化与土体超固结比OCR、静止侧压力系数K0、土体有效内摩擦角φ′、土体水平向渗透系数kh等土体性质密切相关.为研究土体基本物理力学参数对桩周土体强度的影响,土体基本参数按3.1节中取值,计算分析时分别改变其中某项参数,其余参数保持不变.
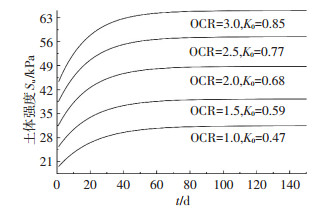
3.2.1 超固结比OCR图 6为不同超固结比的土体中桩周土体强度su随时间t的变化规律,在计算过程中认为超固结比OCR与静止侧压力系数K0之间存在如下关系[24]:
|
图 6 不同超固结比OCR下土体强度随时间变化曲线 Figure 6 Variation of soil strength with time factor for different OCRs |
| $ {K_0} = \left( {1-\sin \varphi '} \right){\rm{OC}}{{\rm{R}}^{\sin \varphi '}}. $ | (34) |
从图 6的计算结果可以看出,沉桩结束后土体强度随超孔压的消散在固结初期迅速提高,且对于正常固结土(OCR=1)而言,最终土体强度约为先期土体强度的1.5倍;对于弱超固结土(1 < OCR < 3)而言,最终土体强度约为先期土体强度的2倍,说明土体OCR越大,沉桩结束后强度增长的幅度越大.
3.2.2 土体内摩擦角φ′图 7为土体有效内摩擦角不同时桩周土体强度随时间的变化规律.土体有效内摩擦角φ′越大,沉桩结束后其对应的强度越大.

|
图 7 不同有效内摩擦角φ′下土体强度随时间变化曲线 Figure 7 Variation of soil strength with time factor for different φ′ |
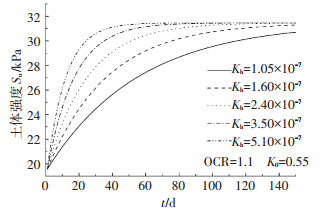
图 8为土体水平向渗透系数kh不同时桩周土体强度随时间的变化规律.沉桩结束后,土体水平向渗透系数kh越大,强度增长速度越快,但土体长期强度与水平向渗透系数kh无关.
|
图 8 不同水平向渗透系数kh下土体强度随时间变化曲线 Figure 8 Variation of soil strength with time factor for different kh |
1) 基于K0-MCC弹塑性本构模型推导了静压桩沉桩过程中桩周土体应力及孔压的解析解,并以此为条件利用固结微分方程得到超孔压消散的级数解答,在此基础上得到桩周土体强度在任意时刻的解答.该解答考虑了土体的初始各向异性、应力历史及松弛效应对土体强度的影响,从而能够较为合理地反映出沉桩结束后桩周土体强度的时变规律.
2) 静压桩在沉桩的过程中产生超孔隙水压力,沉桩结束后超孔隙水压力沿径向消散,但由于土体的松弛效应,仅有部分孔隙水压力转化为土体的有效应力,土体强度在短时间内迅速提高,之后缓慢增加并逐渐趋于稳定值.本文提出的理论计算结果与离心机试验结果均能良好地反映出上述现象.
3) 通过与离心机试验结果对比发现,本文提出的理论方法能够较为合理地预测出桩周土体强度与超孔压的变化规律.但是,在桩周土体强度的预测上,由于没有考虑土体的触变作用使得预测结果偏大,故此方法仍有待进一步改进.
4) 土体性质会对桩周土体强度的变化规律造成一定影响.水平向渗透系数仅影响土体强度增长的速度,而超固结比与有效内摩擦角则影响土体的长期强度,并且随着土体超固结比与土体有效内摩擦角的增加,土体的长期强度也随之增加,沉桩效应亦更加显著.
| [1] | LARS O, ODERBER G. Consolidation theory applied to foundation pile time effects[J]. Géotechnique, 1962, 12 (3) : 217-225. DOI: 10.1680/geot.1962.12.3.217 |
| [2] | COOKE R W, PRICE G. Strain and displacements around friction pile[C]//The 8th International Symposium on Mechanics of Foundation. Houston: Texas University, 1973. |
| [3] |
李雄, 刘金砺. 饱和软土中预制桩承载力时效的研究[J].
岩土工程学报, 1992, 14 (4) : 9-16.
LI Xiong, LIU Jinli. Time effect of bearing capacity of driven pile in saturated soft soil[J]. Chinese Journal of Geotechnical Engineering, 1992, 14 (4) : 9-16. |
| [4] |
龚晓南, 李向红. 静力压桩挤土效应中的若干力学问题[J].
工程力学, 2000, 17 (4) : 7-12.
GONG Xiaonan, LI Xianghong. Several mechanical problems in compacting effects of static piling in soft clay ground[J]. Engineering Mechanics, 2000, 17 (4) : 7-12. |
| [5] |
徐永福, 傅德明. 结构性软土中打桩引起的超孔隙水压力[J].
岩土力学, 2000, 21 (1) : 52-55.
XU Yongfu, FU Deming. Excess pore pressure induced in piling in saturated structural soft soils[J]. Rock and Soil Mechanics, 2000, 21 (1) : 52-55. |
| [6] |
高子坤, 施建勇. 饱和黏土中沉桩挤土形成超静孔压分布理论解答研究[J].
岩土工程学报, 2013, 35 (6) : 1109-1114.
GAO Zikun, SHI Jianyong. Consolidation solution of soil around single-pile after pile sinking[J]. Chinese Journal of Geotechnical Engineering, 2013, 35 (6) : 1109-1114. |
| [7] | BISHOP A W, BJERRUM L. The relevance of the triaxial test to the solution of stability problems[J]. Geotechnical Special Publication, 2002, 118 : 690-754. |
| [8] | VESIC A S. Expansion of cavities in infinite soil mass[J]. Primary Care, 1973, 33 (1) : 75-91. |
| [9] | WROTH C P. The interpretation of in situ soil tests[J]. Géotechnique, 1984, 34 (4) : 449-489. DOI: 10.1680/geot.1984.34.4.449 |
| [10] | RANDOLPH M F, CATER J P, WROTH C P. Driven piles in clay-the effects of installation and subsequent consolidation[J]. Géotechnique, 1979, 29 (4) : 361-393. DOI: 10.1680/geot.1979.29.4.361 |
| [11] | RANDOLPH M F. Science and empiricismin pile foundation design[J]. Géotechnique, 2003, 53 (10) : 847-875. DOI: 10.1680/geot.53.10.847.37518 |
| [12] | OHTA H. Undrained stability of K0 consolidated clays[J]. Proc Icsmfe, 1985, 2 : 613-616. |
| [13] |
张冬梅, 黄宏伟. 不同应力历史条件下软黏土强度时效特性[J].
同济大学学报, 2008, 36 (10) : 1320-1326.
ZHANG Dongmei, HUANG Hongwei. Time-dependency of undrained behavior of natural soft clay with different pre-shearing stress history based on laboratory test[J]. Journal ofTongji University, 2008, 36 (10) : 1320-1326. |
| [14] |
宰金珉, 王伟, 王旭东, 等. 静压桩引起的超孔隙水压力及单桩极限承载力预测[J].
工业建筑, 2004, 34 (8) : 33-35.
ZAI Jinmin, WANG Wei, WANG Xudong, et al. Prediction of excess pore water pressure resulted from static pressed pile and time-dependent pile ultimate bearing capacity[J]. Industrial Construction, 2004, 34 (8) : 33-35. |
| [15] | SUN D A, MATSUOKA H, YAO Y P. An anisotropic hardening elastoplastic model for clays and sands and its application to FE analysis[J]. Computers and Geotechnics, 2004, 31 (1) : 37-46. DOI: 10.1016/j.compgeo.2003.11.003 |
| [16] | YAO Y P, SUN D A. Application of Lade's criterion to Cam-clay model[J]. Journal of Engineering Mechanics, ASCE, 2000, 126 (1) : 112-119. DOI: 10.1061/(ASCE)0733-9399(2000)126:1(112) |
| [17] | SUN D A, MATSUOKA H, YAO Y P. An anisotropic hardening elastoplastic model for clays and sands and its application to FE analysis[J]. Computers and Geotechnics, 2004, 31 (1) : 37-46. DOI: 10.1016/j.compgeo.2003.11.003 |
| [18] | CARTER J P, RANDOLPH M F, WROTH C P. Stress and pore pressure changes in clay during and after the expansion of a cylindrical cavity[J]. International Journal for Numerical & Analytical Methods in Geomechanics, 1979, 3 (4) : 305-322. |
| [19] | SIVAKUGAN N, HOLTZ R D. Anisotropy of undrained shear strength of clays under axi-symmetric loading conditions[J]. Soils and Foundations, 1985, 26 (1) : 132-133. |
| [20] |
王立忠, 叶盛华, 沈恺伦, 等. K0固结软土不排水抗剪强度[J].
岩土工程学报, 2006, 28 (8) : 970-977.
WANG Lizhong, YE Shenghua, SHEN Kailun, et al. Undrained shear strength of K0 consolidated soft clays[J]. Chinese Journal of Geotechnical Engineering, 2006, 28 (8) : 970-977. |
| [21] |
蔡国军, 刘松玉. 基于CPTU测试的桩基承载力预测新方法[J].
岩土工程学报, 2010, 32 (S2) : 479-482.
CAI Guojun, LIU Songyu. New method based on CPTU data to evaluate pile bearing capacity[J]. Chinese Journal of Geotechnical Engineering, 2010, 32 (S2) : 479-482. |
| [22] |
蔡国军, 刘松玉, 童立元, 等. 基于聚类分析理论的CPTU土分类方法研究[J].
岩土工程学报, 2009, 31 (3) : 416-424.
CAI Guojun, LIU Songyu, TONG Liyuan, et al. Soil classification using CPTU data based upon cluster analysis theory[J]. Chinese Journal of Geotechnical Engineering, 2009, 31 (3) : 416-424. |
| [23] | SENNESET K, SANDVEN R, JANBU N. Evaluation of soil parameters from piezocone tests[J]. Transportation Research Record, 1989 : 24-37. |
| [24] | MAYNE P W, KULHAWY F H. K0-OCR relationships in soils[J]. Journal of Geotechnical Engineering, 1982, 108 (6) : 851-872. |
 2016, Vol. 48
2016, Vol. 48


