2. 伊利诺伊大学香槟分校 农业与生物技术工程学院, Illinois 61802
2. Department of Agriculture and Biological Engineering, University of Illinois at Urbana-Champaign, 61802 Illinois, USA
在地势平坦的农田区域下设置浅层排水系统管道,能够有效地提高产量,但同时加速了污染物进入水体的速度,尤其是加速了磷元素的流失[1].中国在华北和长江以南地区的一些农田中设置有浅层排水系统,但对该问题的研究和理解处于起步阶段,在基本理论研究上更是缺乏,各因素对污染物输出的影响及面源污染控制工程方法的研究上,依然有很多问题亟待解决.美国中部地区大约2 000万公顷的农田设置有浅层排水系统[2],因此,美国对于该问题进行了一系列的研究,探索影响排水过程中污染物含量的因素[3-7],但对于多影响因素的协同作用及相互关系还未见报道.本文选取美国中部地区一个具有浅层排水系统的小型农业流域进行监测,分析与磷流失相关的影响因素,并通过主成分分析方法对最主要的影响成分进行分析和识别.
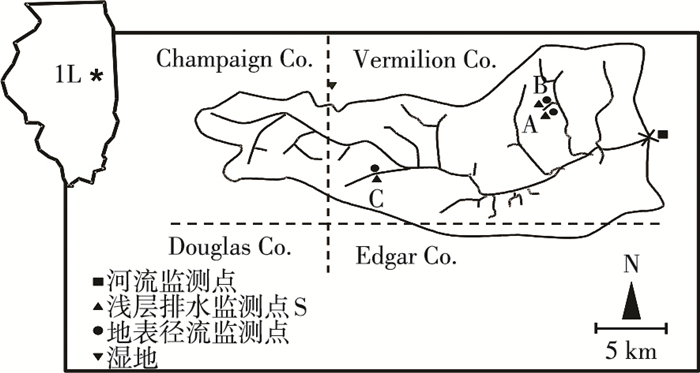
1 研究区域及监测数据Little Vermilion River流域位于美国伊利诺伊州东部中心位置(如图 1所示),其中虚线为郡边界,流域中心坐标为(40°06′ 21.45″N, 87°41′ 34.12″W),河流总长为94.8 km,流域面积489 km2,平均坡度低于1%.其中89.5%的面积为农田,主要作物为玉米与大豆轮作,少量牧草和其他经济作物[8].该地区农田浅层排水应用区域高达70%.根据流域干流、支流特点及周边农田特点,设置3个浅层排水监测点(As、Bs、Cs),3个地表径流监测点(A、B、C).监测指标包括:日降雨量、日最高、低温度、施肥量、地表径流量、浅层排水流量、植被覆盖率、植物生长周期干质量变化、地表蒸腾量、地表径流磷酸盐PO4-、浅层排水中磷酸盐PO4-.
|
图 1 研究区域示意及采样点布置 |
浅层排水系统中水样的采集采用自动与监测技术,所有的监测点A、B、C均安装了8-in Palmer-Bowlus flumes©自动采样系统,安装位置为浅层排水系统干管入渠的出口人孔处,方便定期提取样品和数据.其中自动采样的频率为每天3次(化验工作由伊利诺伊大学香槟分校农业与生物技术学院水质分析实验室进行).为了防止特殊气象条件影响样本代表性,添加人工取样,两周1次,同时收集采样器中样品.监测数据包括磷酸盐浓度和流量.
2.2 气象数据气象数据中降雨量的测量采用倾斜斗式雨量计量器.计量器设置在地表径流监测点相邻位置,因为A点与B点相邻共用一个计量器,通过远程通讯方式连接实验室服务器,数据更新的频率为每天.采用铜-康铜热电偶组进行日最高、最低气温的测量,同样连接远程服务器.
2.3 耕作管理数据农田的耕作管理和作物类型由农场主根据实际情况和经验决定,其中包括化肥施用量、农药施用量、耕作细节、收获时间等,通过与农场主沟通,及时跟踪记录数据.
3 研究方法及数据处理 3.1 研究方法PCA(principal component analysis)译为主元分析/主成分分析,是一种对数据进行分析的技术,最重要的应用是对原有数据进行简化[9-10].由主成分分析法构造回归模型,即将各主成分作为新自变量代替原来自变量x做回归分析.用主成分分析筛选回归变量.回归变量的选择具有重要的实际意义.为了使模型本身易于做结构分析、控制和预报,可以从原始变量所构成的子集合中选择最佳变量,构成最佳变量集合.用主成分分析筛选变量,可以用较少的计算量选择变量,获得选择最佳变量子集合的效果[11].选取的参数有:温度(监测); 植被类型(监测); 散蒸发(监测); 覆盖系数(监测+估算)[12]; 作物干质量(估算)[13]; 流量(径流或管内流)(监测); 降雨量(监测); 施肥量(磷)(监测); 耕作内容(监测+数字代换); 磷流失总量(监测).
其基本数学原理如下:
1) 原始指标数据的标准化采集.p维随机向量x = (x1, x2, ..., xp)T,n个样品xi= (xi1, xi2, ..., xip)T,i=1, 2, …, n.
n>p时,构造样本阵,对样本阵元进行如下标准化变换:
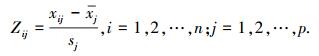
|
其中, 
2) 对标准化阵Z求相关系数矩阵, 即
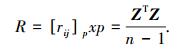
|
其中, 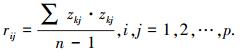
3) 解样本相关矩阵R的特征方程|R-λIp|=0得p个特征根, 确定主成分.
4) 将标准化后的指标变量转换为主成分,即
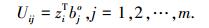
|
U1称为第一主成分,U2称为第二主成分, …, Up称为第p主成分.
5) 对m个主成分进行综合评价.
对m 个主成分进行加权求和,即得最终评价值,权数为每个主成分的方差贡献率.
3.2 数据处理方法首先将一些定义类的监测指标数据化.对耕作内容进行数据化,依据是以俄亥俄州立大学对不同耕作内容对水质的影响程度分类为参考[14],如表 1所示.对5种主要的耕作内容进行了定义,其中施肥将会对土壤水分的溶解性营养指标有3级影响,对吸附性营养物质也具有3级影响,而耕耘过程也会对营养物产生3级影响(翻耕土地能够使土壤空隙的比表面积增大,以及降雨后空隙中水分与营养元素接触的比例增大,从而加剧流失)等.
| 表 1 耕作对地表及浅层排水水质影响等效等级 |
然后通过公式将监测的耕作内容转化为数字形式以供分析,即
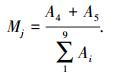
|
式中:i为参数范围1~9;j为耕作内容1~5;Ai为水质指标.只选择A4与A5计算等效影响等级是因为只考察影响元素的迁移.
作物类型数字化以作物植株的大小排序,本研究中作物只包含玉米、大豆,所以数字化形式大豆为1,玉米为2.
植被覆盖因子的计算根据美国土壤流失模型USLE中对于裸露土壤及不同植被覆盖率的定义进行,定义裸露土壤的覆盖系数为C≥1,非农田的土壤覆盖系数由植被的密度和植被残茬量计算而得,农田的覆盖系数则根据不同作物在不同生长期给予定义数值.
其他7个影响因素均为实测数据,为了去除量纲的影响,所有数据均进行了标准化.
4 结果与分析 4.1 主成分结果通过主成分分析方法对多因素关系矩阵进行降维,同时对主成分抽取、旋转、分析其所包含的因素的直接关系,并结合数据的实际意义对主成分进行定义,进而分析影响磷元素迁移的最主要成分.主成分分析前先对所有影响因素的相关性进行分析,如表 2所示,可以看出,所有影响因素都存在显著相关关系,如植被类型与覆盖系数、温度、蒸腾量呈显著相关(P<0.001),降雨量也与覆盖系数呈显著相关等,说明各影响因素之间都存在一定的相关关系.因此,抽取主成分并将多元数据进行降维是可行且有意义的.
| 表 2 所有影响因素上三角相关系数矩阵 |
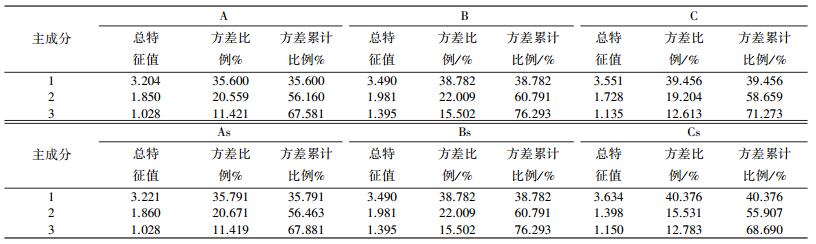
表 3是各点抽取的主成分所有影响因素对磷酸盐流失影响方差的解释度.可以看出,所有点抽取的3个主成分均能够解释9个影响因素的70%方差及以上,说明抽取的主成分具有代表性,一般的统计教程上推荐方差解释度达到85%,但对于自然科学中的实际问题,方差解释度可以根据具体问题灵活确定.
| 表 3 各点地表及浅层排水主成分方差解释量 |
抽取的主成分方差解释度没有达到85%,是由于土壤、地形等因素在本研究所有监测点均相同,这些相同因素没有包含在主成分抽取过程中,导致方差解释度不高.但不影响通过抽取主成分并发现各影响因素之间的关系,推断出最主要影响成分和最主要影响因素.通过表 3可以看出,在主成分中第一主成分占的方差解释度最大,平均达35%以上.进一步分析主成分抽取过程,发现所有监测点及其对应的地表径流和浅层排水数据均显示出类似的主成分趋势,意味着在该多重主成分分析过程中,6组数据显示出相同的趋势,这也说明即使在不同地点、不同的排水类型,这9个影响因素均会对其产生相同的影响,即以3大类主要影响类型的作用方式存在.
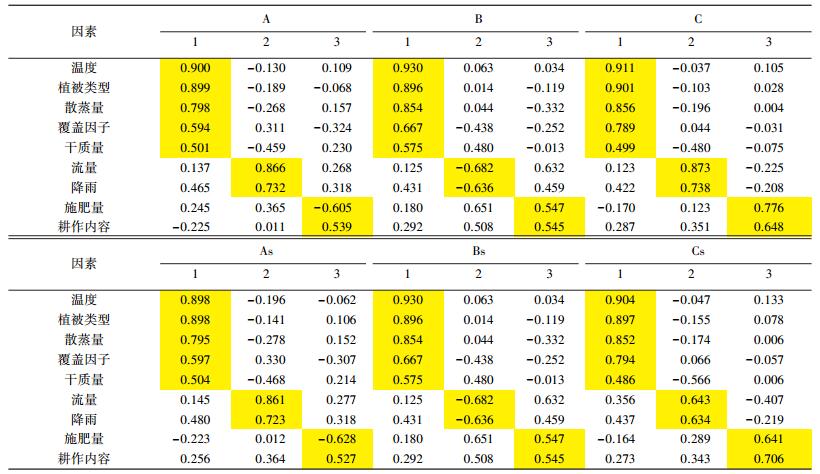
进一步对各影响因素在各主成分的载荷量数据进行分析,表 4为各因素在主成分方向上投影的载荷量.之前论证了各组数据存在显著差异,但通过标示的载荷量数据可以看出,所有6组主成分中均显示出相同的因素分布,其中第一主成分主要包括温度、植被类型、散蒸量、覆盖因子、干质量,第二主成分包括流量及降雨,第三主成分包括施肥量及耕作内容,这说明抽取的主成分对磷元素迁移影响显示出同质性.
| 表 4 各点主成分载荷量 |
并且主成分中的影响因素在对应主成分中的载荷分量具有规律性.例如A中第一主成分中温度的载荷量最大,为0.900,其他5组数据也有相同结果,说明在不同组不同排水形式中温度起到的影响作用类似,同理可得其他影响因素具有相同特点.其中一个值得关注的现象是各主成分载荷最高的影响因素分别为温度、流量、施肥量.
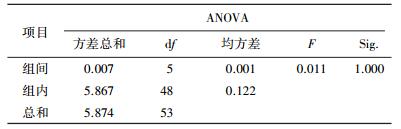
进一步对各组数据的主成分载荷量进行方差分析,结果如表 5.可以看出,6组载荷量数据在组间与组内均差异不显著,显著性水平为1.000,其意义为方差同质,所进行的主成分抽取得到相同结果,进一步说明在不同条件下9因素对磷迁移的影响一致.
| 表 5 组间及组内方差同质性检验 |
将主成分进行旋转得到主成分向量空间分布图(图 2).可以看出,各主成分分别对应各自的坐标轴分布,呈现正交趋势,说明抽取的主成分在某种程度上相互无关,呈现出相应的独立特性,而在主成分中的因素则是因为共有一致特性相互空间上靠近.如图 2中三角块代表主成分1中5个因素的空间向量,因为具有类似的属性,并且对磷流失的影响具有相似之处,其在空间中相互聚拢,旋转过后趋向同一个维度.

|
A, B, C, As, Bs, Cs分布代表A、B、C 3点地表径流及浅层排水数据组,向量1~9分别代表温度、植被类型、散蒸量、覆盖因子、作物干质量、流量、降雨、施肥量及耕作内容. 图 2 各点主成分磷流失量相关主成分3-D空间分布 |
对第一主成分的所有影响因素进行分析发现,温度、植被类型、散蒸量、覆盖因子、干质量等均为与作物生长有关的参数,如温度是作物生长的直接驱动力(来源于光照)从而在该主成分中贡献载荷量最高,而且温度也直接影响磷酸盐的迁移.其次是植被类型,不同植被对于磷酸盐的利用量也不同,玉米的植株重量大于大豆几十倍,所需吸收的磷酸盐量也远远超过大豆.同理散蒸量的多少也与作物的生长情况有关,植物枝叶茂密则蒸腾量大,而枝叶茂密则导致地表的蒸发量减少,对土壤水分的含量产生一定的影响.覆盖因子大说明覆盖率高,减少降雨对地表的冲击,从而减少磷酸盐在地表的流动.作物干质量则是有效消耗土壤中磷元素的途径,通过作物吸收合成转化为有机磷.所以,以上所有影响因素均与作物有关,通过它们的实际意义可以定义为生物主成分.
第二主成分包括流量和降雨,根据其特性可以命名为水力主成分.
第三主成分包括施肥量和耕作内容,其中施肥量已经在之前的分析中提到,耕作内容对流失的影响包括初春翻耕加剧污染物的流失,收获方式(机械收割后粉碎秸秆或保留残茬)、播种方式(育苗或播种)会对土壤的状态进行改变,从而改变其营养元素流失特性.该两个影响因素均为主观性的干预因素,人为作用明显,因此命名为人为干预主成分.此3个主成分代表了多影响因素对磷流失的主要影响类型.
4.2 回归分析结果对主成分采用多元线性回归方式,参数进入方式为全进入,这是因为主成分分析的目的即为降维,9因素降维三主成分后,由于参数较少可以选择参数全进入方式,以避免向前或向后回归参数进入方式造成的误差.磷酸盐流失的回归结果如图 3所示,磷酸盐流失的回归模型拟合度在浅层排水与地表径流流失量都不理想,浅层排水模型的拟合度略优于地表径流模型.其中A点浅层排水模拟的拟合度最差.

|
图 3 回归分析结果与标准化后磷酸盐流失量对比 |
从模型系数矩阵表 6的结果可以发现,对于磷酸盐流失模型,浅层排水与地表径流对应模型中水力主成分系数C2的显著性水平为极显著(P<0.01),而生物主成分和人为干预主成分的系数均不显著,并且发现所有的C1与C3值均低于0.2,说明低于20%的该二主成分与磷酸盐流失有关,而且所有模型的相关性系数均低于0.4,说明模型模拟效果差.由于模型的自变量进入方式为全进入,得到的系数为最优方程系数,在最优系数的条件下,模型的相关性系数低,说明自变量对因变量的影响不大.所以,磷酸盐的迁移过程中,虽然水力主成分占主要作用,但其最终的影响依然不大.
| 表 6 磷酸盐流失多元线性回归模型系数与显著性 |
1) 各因素均对磷流失产生影响,表现为多因素协同作用,多个因素之间存在显著相关性.
2) 9影响因素可以降维为3个主要影响成分,根据其实际意义分为:生物主成分,包括温度、覆盖因子、植被类型、散蒸量、干质量;水力主成分,包括流量和降雨量;人为干预主成分,包括施肥量及耕作内容.
3) 回归分析结果发现水力主成分对磷流失的贡献量最大,为70%,且对浅层排水和地表径流流失均呈显著相关;生物与人为干预主成分对磷酸盐流失有一定影响,但贡献率不高.
4) 通过模拟污染物输出及控制过程,比较各控制方法的优略,对该地域及相似流域非点源污染控制方案的制定提供重要的科学依据.
| [1] |
KALITA P K, COOKE R A C, ANDERSON S M, et al. Subsurface drainage and water quality:the Illinois experience[J]. Trans ASABE, 2007, 50(5): 1651-1656. DOI:10.13031/2013.23963 |
| [2] |
SKAGGS R W, FAUSEY N R, EVANS R O. Drainage water management[J]. J Soil Water Conserv, 2012, 67(6): 167a-172a. DOI:10.2489/jswc.67.6.167A |
| [3] |
UPADHYAYA A. Hybrid finite analytic solution for computation of spacing between drains in sloping lands[J]. J Irrig Drainage Eng-ASCE, 2013, 139(2): 131-136. DOI:10.1061/(ASCE)IR.1943-4774.0000498 |
| [4] |
VERACHTERT E, VAN DEN EECKHAUT M, POESEN J, et al. Spatial interaction between collapsed pipes and landslides in hilly regions with loess-derived soils[J]. Earth Surf Process Landf, 2013, 38(8): 826-835. DOI:10.1002/esp.v38.8 |
| [5] |
XU L G, NIU H L, XU J, et al. Nitrate-nitrogen leaching and modeling in intensive agriculture farmland in China[J]. Sci World J, 2013, 10: 2-10. |
| [6] |
LI G, CHEN C. Applied mechanics and materials I, Pts 1-3[M]. Stafa-Zurich: Trans Tech Publications Ltd, 2013: 2821-2826.
|
| [7] |
ZGORELEC Z, MESIC M, JURISIC A, et al. Leached phosphorus measured in drainage water through a field experiment with varying nitrogen rates[J]. J Environ Prot Ecol, 2013, 14(2): 463-467. |
| [8] |
COOKE R, VERMA S. Performance of drainage water management systems in Illinois, United States[J]. J Soil Water Conserv, 2012, 67(6): 453-464. DOI:10.2489/jswc.67.6.453 |
| [9] |
GVOZDIC V, BRANA J, MALATESTI N, et al. Principal component analysis of surface water quality data of the River Drava in eastern Croatia (24 year survey)[J]. J Hydroinform, 2012, 14(4): 1051-1060. DOI:10.2166/hydro.2012.063 |
| [10] |
GU J F, ZHU C J, HAO Z C. Application of principal com-ponent analysis in water quality evaluation by spss software[J]. Adv Mater Res-Switz, 2012, 403-408: 3277-3280. |
| [11] |
HAO R X, LI S M, LI J B, et al. Water quality assessment for wastewater reclamation using principal component analysis[J]. J Environ Inform, 2013, 21(1): 45-54. DOI:10.3808/jei.201300231 |
| [12] |
BENGTSON R L, SABBAGH G, USLE P. Factors for subsurface drainage on low slopes in a hot, humid climate[J]. J Soil Water Conserv, 1990, 45(4): 480-482. |
| [13] |
BOARD J E, WIER A T, BOETHEL D J. Source strength influence on soybean yield formation during early and late reproductive development[J]. Crop Sci, 1995, 35(4): 1104-1110. DOI:10.2135/cropsci1995.0011183X003500040031x |
| [14] |
Ohio State University. Ohio State University extension fact sheet[EB/OL]. [2015-01-15]. http://ohioline.osu.edu/aex-fact/0464.html.
|
 2016, Vol. 48
2016, Vol. 48