2. 哈尔滨工业大学 市政环境工程学院, 150090 哈尔滨;
3. 哈尔滨工业大学 能源科学与工程学院, 150001 哈尔滨
2. School of Municipal and Environmental Engineering, Harbin Institute of Technology, 150090 Harbin, China;
3. School of Energy Science and Engineering, Harbin Institute of Technology, 150001 Harbin, China
气液两相流的数值模拟是多相流领域的研究热点,目前国内外关于气液两相流数值模拟的公开文献大部分在选择湍流模型时主要依靠经验,且采用在单相流中得到广泛应用的二方程模型[1-8].其中模拟水平管内流型的文献多数不涉及环状流这一常见流型[2-8],个别文献模拟了该流型但是得到的环状流效果差[1], 少数文献采用雷诺应力模型(RSM)得到了较理想的水平管环状流效果,但是文献并未分析选择RSM模型的原因[9].目前尚未见到有文献分析气液两相流中的湍流和单相流中的湍流之间的关系和区别,导致两相流数值模拟中,湍流模型的选择主要靠经验,缺乏理论依据.
二方程模型是基于各向同性湍流理论建立起来的,理论上只适用于各向同性湍流,该模型对于一般的单相流动具有较高的精度和计算效率,因此被广泛应用.然而二方程模型用于气液两相流的数值模拟时,某些情况下的适用性还有待分析,因为气液界面处不同方向的物性变化差异很大,气液界面处的湍流可能会偏离各向同性,某些情况下采用二方程模型可能得不到准确结果.本文将对管内气液两相流界面湍流各向异性特性进行分析,在此基础上探讨管内气液两相流湍流模型的选择依据,为气液两相流的数值模拟研究提供理论参考.
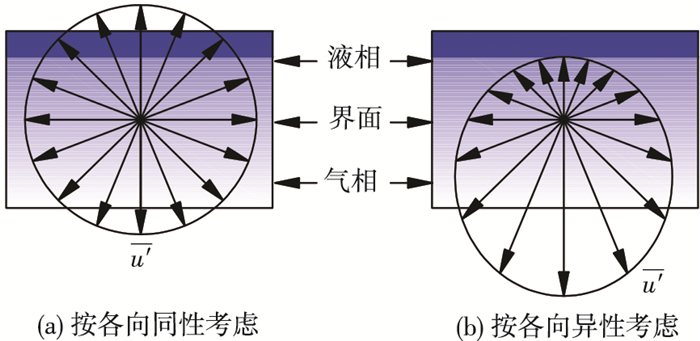
1 水平管内界面湍流各向异性特性分析在管内气液两相流界面处任意取一点来分析其脉动速度场,由于脉动速度随时间波动,故本文主要讨论其平均特性.因液相的密度和动力粘度远大于气相,故该点不同方向上的脉动速度平均值不同;在垂直于界面方向上气液平均物性变化率最快,故指向气相的脉动速度平均值最大,而指向液相的脉动速度平均值最小,其他方向的脉动速度平均值介于二者之间,不同方向上的脉动速度矢量构成椭圆形,如图 1所示.由动量定理可知,这种椭圆形速度场在不同方向上的动量不能完全抵消,会产生一个垂直于界面且指向液相的附加作用力,本文称之为湍流惯性力,如图 2所示.显然湍流惯性力的大小与界面湍流各向异性的显著程度有关,当气液流速较小时,脉动速度较小,不同方向上脉动速度平均值的差异也较小,此时湍流各向异性不显著,湍流惯性力较小;当气相流速较大且气液之间存在较大的剪切力时,指向气相的脉动速度平均值会显著大于指向液相的脉动速度平均值,此时湍流各向异性十分显著,湍流惯性力也较大.
|
图 1 界面湍流不同方向上的脉动速度平均值示意 |

|
图 2 界面湍流各向异性产生的作用力示意 |
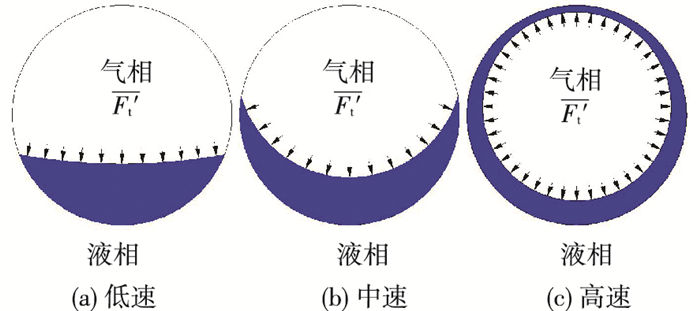
在水平管内,湍流惯性力与重力相互作用可呈现不同的流型.当气相流速较低时,因湍流惯性力较小,其相对于重力可忽略,故呈现分层流的特性,如图 3(a)所示.随着气相流速增加湍流惯性力也随之增加,当其大小与重力相当时湍流惯性力会改变液面形状.实际上分层流液体表面的湍流惯性力是不均匀的,中间位置因远离壁面其流速较大,湍流惯性力大,靠近壁面的位置因为壁面效应其流速较小,湍流惯性力小,这种力分布会使靠近壁面的液体沿着管壁向上流动形成半环状流,如图 3(b)所示.当气相流速继续增加以至于湍流惯性力占主导时,液膜将布满整个管壁形成环状流,如图 3(c)所示.水平管内环状流上部的液膜之所以能维持稳定有3个方面的原因:一是管下部的湍流惯性力方向向下,可以阻止上部的液膜向下流动;二是管上部的湍流惯性力方向向上,为上部的液膜提供支撑;三是液体表面张力维持了液膜的稳定性,防止其破碎.当气相流速足够大时,湍流惯性力远大于重力,上下壁面的液膜厚度会趋于一致.文献[10-11]指出气相流速越大,水平管中环状流越对称,与上述分析结果一致.
|
图 3 水平管内气液界面形状随流速的变化 |
上述结论是把气液界面湍流按各向异性考虑的结果,如果界面处的湍流按各向同性来考虑,则脉动速度在不同方向上的平均值相等,不同方向的速度矢量构成一个圆形,如图 1(a)所示.由动量定理可知这种速度场在不同方向上的动量相互抵消,不会产生如前所述的湍流惯性力.无论气相流速多大,按各向同性考虑得到的流型都将是分层流,如图 3(a)所示.这表明水平管内界面湍流按各向同性考虑将难以得到环状流的效果.
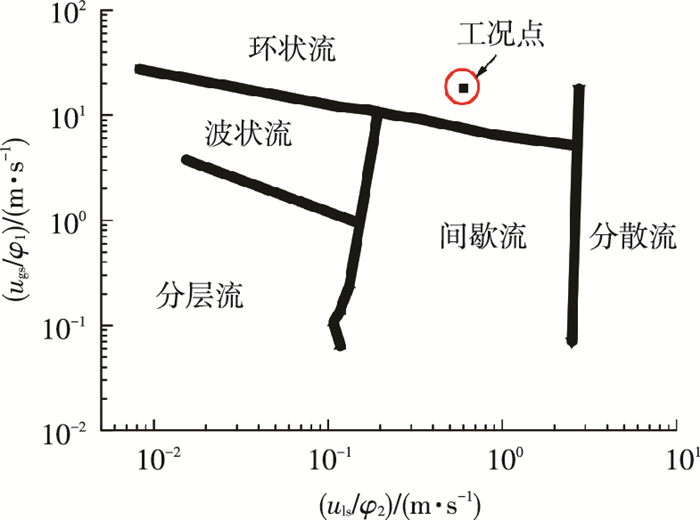
2 分析结果的验证上述分析表明,如果湍流模型按各向异性考虑则可以模拟出水平管内的环状流效果,如果按各向同性考虑将得到分层流的效果.为了验证上述分析的正确性,本文在Weisman水平管流型图[12-13]中选取一个典型的环状流工况,见图 4(ugs、uls分别表示气相和液相折算速度,φ1、φ2为修正系数),工况参数见表 1,分别用各向同性和各向异性湍流模型对其进行模拟,通过比较结果进行验证.
| 表 1 计算工况参数 |
本文选择应用最广泛的k-ε、k-ω二方程模型作为各向同性湍流模型的代表.二方程模型是基于涡粘性假设[14]建立起来的,涡粘性假设将湍流粘性与分子粘性相比拟,认为湍流运动和分子运动一样具有各向同性特征,其计算雷诺应力的公式[14]为
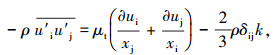
|
式中μt为湍流粘性系数,k为湍动动能.
本文选择雷诺应力模型(RSM)[14-15]作为各向异性湍流模型的代表.RSM模型彻底抛弃了各向同性的涡粘性假设,直接建立雷诺应力的输运方程,方程形式[14-15]为
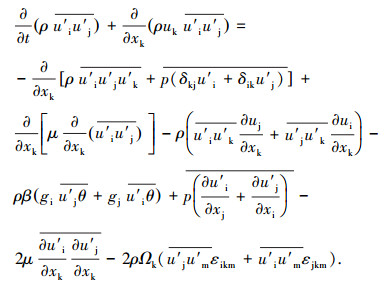
|
理论上RSM模型相对于二方程来说能更好地描述各向异性湍流问题,实践也证明RSM模型对各向异性湍流有良好的表现,如文献[16-17]指出,对于旋流器中各向异性流场,对比常用的二方程模型和RSM模型的预测结果,RSM模型的预测最准确.
分别用二方程模型和RSM模型来模拟图 4中的环状流工况,计算模型和边界条件为:多相流模型采用三维瞬态VOF模型,表面张力采用连续表面张力模型[18],入口边界条件根据气、液流速换算成质量流率,出口为自由出流边界条件,壁面为无滑移绝热壁面,湍流模型分别选取k-ε、k-ω、RSM,近壁面处理方法选择标准壁面函数,离散格式除时间项采用一阶隐式,体积分数采用Geo-Reconstruction,压力采用PRESTO!外,其他均用二阶迎风格式,求解方法采用PISO算法.根据几何结构划分六面体网格,网格数为64万.基于ANSYS Fluent 14.0软件将上述模型和边界条件进行相应的设置,模拟得到的出口处流型结果见图 5、6.

|
图 5 二方程模型模拟出的流型(颜色表气相体积分数) |

|
图 6 RSM模型模拟出的流型(颜色表气相体积分数) |
二方程模型k-ε、k-ω模拟出来的流型效果基本一致,均表现出分层流的结果,与流型图不符,见图 5;而RSM模型则得出环状流的结果,与流型图结果一致,见图 6.二方程模型和RSM模型的模拟结果与本文分析一致,表明本文关于界面湍流各向异性的分析正确.
从细节上看,图 5(a)中的分层流界面不完全呈现一条水平线,这是因为丙烷的壁面接触角缺乏数据,采用的是模型默认值90°,故在表面张力作用下就呈现出图 5的效果.图 6中液膜分布在管壁四周,管上部液膜清晰可见,气相在管中心流动,是比较成熟的环状流,而且气液界面的波动也表现的很清楚,见图 6(b).综上所述,无论从流型的种类,还是流型的细节方面,水平管内环状流的模拟适合选用RSM模型,而不适合选用二方程模型.
3 水平管内气液两相流湍流模型的选择依据湍流模型有很多,本文不一一讨论,只对广泛应用的二方程模型和RSM模型进行讨论.二方程模型只能得到平均速度,无法得到脉动速度,只适用于各向同性湍流;RSM模型可以得到平均速度和脉动速度,对于各向同性和各向异性湍流均适用,故其适用范围必然比二方程模型广泛.但是RSM模型计算量大,收敛相对困难,因此并不希望在任何情况下都选择RSM模型.事实上界面湍流各向异性特性并非任何时候都很显著,而且湍流惯性力并非总是对流型有很大影响,因此也不是任何情况下都需要选择RSM模型.
当气液之间存在较大剪切力时,界面湍流各向异性十分显著.对于水平管,湍流惯性力克服重力使环状流得以形成和维持,此时应选择RSM湍流模型,不宜采用广泛使用的二方程模型;当气液流速较小时,界面湍流各向异性不显著,选择二方程模型和RSM模型的差异并不大,两类模型均可满足要求.
4 结论1) 水平管内气液两相流界面处不同方向的物性变化率不同导致界面湍流在不同方向上的脉动速度平均值不同,其不同方向上的脉动速度矢量构成椭圆形,从而产生垂直于界面且指向液相的湍流惯性力,该力随着气相流速和气液剪切力的增加而增加,是水平管环状流形成的重要原因.
2) 对于水平管环状流工况,基于各向同性的二方程模型无法模拟出环状流效果,得到的是分层流效果;而基于各向异性的RSM模型可以模拟出较好的环状流效果,该结果与本文分析结果一致,表明本文分析正确.
3) 当水平管内气液之间剪切力较大且湍流惯性力与重力大小相当或者远大于重力时,适合选用RSM模型;其他情况二方程模型和RSM模型均适用.
| [1] |
宫莎莎. 水平混输管路流型研究[D]. 北京: 中国石油大学, 2009.
|
| [2] |
刘殿玮. 水平管内油气水三相流流型研究[D]. 大庆: 东北石油大学, 2011.
|
| [3] |
赵铎. 水平管内气液两相流流型数值模拟与实验研究[D]. 北京: 中国石油大学, 2007.
|
| [4] |
刘夷平. 水平油气两相流流型转换及其相界面特性的研究[D]. 上海: 上海交通大学, 2008.
|
| [5] |
EGOROV Y, BOUCKER M, MARTIN A, et al. Validation of CFD codes with PTS-relevant test cases[R]. Bruxelles: European Commission, 2004.
|
| [6] |
LO S, TOMASELLO A. Recent progress in CFD modelling of multiphase flow in horizontal and near-horizontal pipes[C]//7th North American Conference on Multiphase Technology. Banff: BHR Group, 2010.
|
| [7] |
EKAMBARA K, SANDERS R S, NANDAKUMAR K, et al. CFD simulation of bubbly two-phase flow in horizontal pipes[J]. Chemical Engineering Journal, 2008, 144(2): 277-288. DOI:10.1016/j.cej.2008.06.008 |
| [8] |
余学立. 低含水率原油在倾斜管中的油水两相流数值模拟研究[D]. 北京: 北京交通大学, 2011.
|
| [9] |
孟赵一. 油气润滑系统水平管内环状流形成机理研究[D]. 秦皇岛: 燕山大学, 2011.
|
| [10] |
郭烈锦. 两相与多相流动力学[M]. 西安: 西安交通大学出版社, 2002.
|
| [11] |
陈学俊, 陈立勋, 周芳德. 气液两相流与传热基础[M]. 北京: 科学出版社, 1995.
|
| [12] |
WEISMAN J, KANG S Y. Flow pattern transition for gas-liquid flow invertical and upwardly inclined lines[J]. International Journal of Multiphase Flow, 1981, 7(3): 271-291. DOI:10.1016/0301-9322(81)90022-7 |
| [13] |
WEISMAN J, DUNCAN D, GIBSON J, et al. Effects of fluid properties and pipe diameter on two-phase flowpatterns in horizontal lines[J]. International Journal of Multiphase Flow, 1979, 5(6): 437-462. DOI:10.1016/0301-9322(79)90031-4 |
| [14] |
HINZE J O. Turbulence[M]. New York: McGraw-Hill Publishing Company, 1975.
|
| [15] |
LAUNDER B E. Second-moment closure:present... and future?[J]. Heat Fluid Flow, 1989, 10(4): 282-300. DOI:10.1016/0142-727X(89)90017-9 |
| [16] |
赵立新, 朱宝军. 不同湍流模型在旋流器数值模拟中的应用[J]. 石油机械, 2008, 36(5): 56-60. |
| [17] |
陆耀军, 周力行, 沈熊. 不同湍流模型在液-液旋流分离管流场计算中的应用及比较[J]. 清华大学学报(自然科学版), 2001, 41(2): 105-109. |
| [18] |
BRACKBILL J U, KOTHE D B, ZEMACH C. A continuum method for modeling surface tension[J]. Journal of Computational Physics, 1992, 100(2): 335-354. DOI:10.1016/0021-9991(92)90240-Y |
 2016, Vol. 48
2016, Vol. 48