2. 西安建筑科技大学 土木工程学院, 710055 西安
2. School of Civil Engineering, Xi'an University of Architecture and Technology, 710055 Xi'an, China
如何合理确定台风多发地区建筑结构的设计风速对建筑结构设计而言至关重要.利用台风风场模型结合Monte Carlo数值模拟方法进行足够多次数的台风风场数值模拟,从而获取建筑结构设计所需的设计风速是目前研究者普遍采用的方法[1].此方法首先利用台风历史数据资料确定台风关键参数的概率分布,然后利用Monte Carlo数值模拟方法不断进行抽样,放入台风风场模型、衰减模型进行足够多次数的台风风场数值模拟.最后,利用极值风速分析方法完成特定地区不同重现期下台风极值风速的预测.在整个过程中,有几个核心问题值得注意,首先是台风关键参数概率分布模型的可靠性,此方面主要依靠更多的台风历史数据资料来获取对其分布更好的估计.第二,就是所采用台风风场物理模型的准确性,这方面目前研究者经常采用的主要有Vickery台风风场模型[2]和Meng台风风场模型[3].其中,Vickery台风风场模型为基于大气运动动量方程的模型,需要借助数值差分方法进行求解,耗时较长.Meng台风风场模型则是基于大气运动动量方程来获取台风风场的近似解析解,计算效率相对较高,精度也有保证.但其求解过程仍然涉及循环迭代求解,导致计算过程耗时较多.后续研究中,文献[4-5]一直尝试建立计算效率更高的台风风场模型.另外,在利用台风风场模型进行台风风场数值模拟时,都不可避免地需要利用Holland台风径向气压分布模型[6], 而此模型中关于台风径向气压参数B的取值准确性会对台风风场数值模拟的结果造成很大影响,此问题长久以来未得到很好解决[7-8].
针对以上问题,本文将首先利用从上海台风研究所获取的中国东南沿海1949—2012年的台风历史数据进行台风关键参数概率分布研究,然后借鉴Meng台风风场模型[5]的研究成果,提出台风风场经验模型,并在其中引入新的Holland径向气压分布参数B的估计表达式,最后基于以上研究结合Monte Carlo数值模拟方法,利用台风极值风速分析方法对香港地区不同重现期下的台风极值风速进行预测,验证利用此台风风场模型进行台风极值风速预测的有效性.
1 台风风场经验模型 1.1 梯度风计算此处用于台风风场梯度风计算的台风风场模型来源于Meng台风风场模型[3],此模型的推导基于三维Navier-Stokes方程的水平动量方程,其表达式为
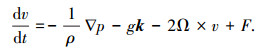
|
(1) |
式中:v为台风风速, m/s;ρ为空气密度, kg/m3;p为大气气压, hPa;▽为三维向量算子;g为重力加速度, m/s2;k为单位向量;Ω为地球自转角速度, rad/s;F为地面摩擦力, N.
在梯度风高度处不考虑摩擦力,风速v变为梯度风vg.为得到式(1)的解析解,假定不受摩擦影响的梯度风vg以台风移动速度c移动,公式变为
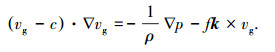
|
(2) |
对式(2),建立坐标原点位于台风中心的圆柱坐标系,假设自由大气中不受摩擦影响的梯度风vg的径向风速分量vrg小于切向风速分量vθg,从而可近似解得切向风速分量vθg.更进一步,利用三维Navier-Stokes方程的连续方程可获得径向风速分量vrg.切向风速分量vθg以及径向风速分量vrg的表达式为:
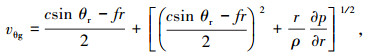
|
(3) |
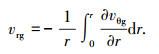
|
(4) |
式中:θr为台风移动方向与台风中心和参考点连线的夹角, (°);f为科氏力常数, s-1;r为径向距离, km.
1.2 Holland径向气压参数B计算公式Holland[6]于1980年提出的台风径向气压分布模型已广泛应用于与台风有关的研究,其表达式为
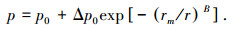
|
(5) |
式中:p0为台风中心气压, hPa;Δp0为台风中心气压差,等于pn-p0;pn为台风边际气压,近似取1 010 hPa;rm为最大风速半径, km;B常利用线性拟合方法得到,通常介于0.5和2.5之间[9].
将式(5)代入式(3),在梯度风高度处的最大风速半径rm处,近似认为vθg等于此处的梯度风vmax,并忽略台风移动速度c对B的影响,从而推导得到式(6)所示新的B计算公式.另外,Holland研究表明[7-8],此计算公式的空气密度ρ不能假设为常数,其可利用三维Navier-Stokes方程的状态方程进行计算,如式(7)~(10)所示.从而B可利用如下公式进行计算:
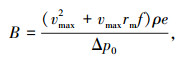
|
(6) |

|
(7) |
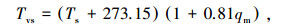
|
(8) |
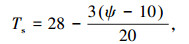
|
(9) |

|
(10) |
式中:vmax为台风最大风速, m/s;e为指数函数的底;R为普适气体常数,等于286.9 J/(kg·K);Tvs为海平面虚温度, K;Ts为海平面温度, ℃;qm为相对湿度90%时的蒸汽压, hPa;ψ为纬度值, (°).
与其它B的计算式相比[7],利用以上公式,借助从气象部门直接获取的台风中心位置、中心气压差Δp0及利用经验公式间接获取的最大风速vmax、最大风速半径rm数据可以方便计算得到台风发生过程中不同时刻对应的B值,实现对不同时刻台风风场更好的模拟.
1.3 地面风速计算在大气边界层内,Ishihara等[5]充分考虑了大气涡流对风速剖面的影响,计算得到大气边界层任意高度z处的台风风速v(z)及风向θ(z),其表达式为:
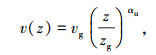
|
(11) |
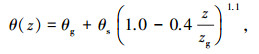
|
(12) |

|
(13) |
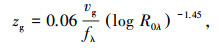
|
(14) |
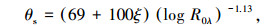
|
(15) |
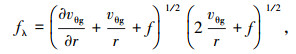
|
(16) |
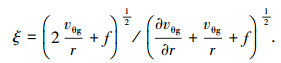
|
(17) |
式中:vg、θg为梯度风速、风向;αu、zg为风速剖面指数及梯度风高度,其为绝对涡旋系数fλ(式(16))及Rosby系数Roλ (=vg/fλz0)的函数;θs为流入角,其为均匀涡旋系数ξ (式(17))及Rosby系数Roλ的函数.
2 台风关键参数概率分布 2.1 台风历史数据本文研究所用的台风历史数据资料来自上海台风研究所记录的1949—2012年台风期间每6 h的台风数据资料[10],并仅考虑香港周围250 km半径范围内的台风数据.
2.2 台风关键参数概率分布估计台风中心气压差Δp0为台风中心与边际气压之差.已有研究表明,利用对数正态分布可以很好地描述其分布.此处同样利用此分布来对香港地区研究范围内的台风中心气压差Δp0数据进行拟合,拟合结果见图 1(a), 此分布的均值和方差分别为3.28和0.59.

|
图 1 台风关键参数概率分布拟合 |
台风移动速度c可利用每6 h台风中心位置进行计算得到,其值介于2~65 km/h.此处利用正态分布对香港地区研究范围内的台风移动速度c数据进行拟合,拟合结果见图 1(b), 此分布的均值和方差分别为18.91和9.08.
台风移动方向θ同样利用每6 h台风中心位置计算得到,并规定正北方向顺时针为正.此处利用双正态分布进行香港地区研究范围内的台风移动方向θ数据的拟合,拟合结果见图 1(c).此分布的负样本的均值及方差分别为-67.58及52.28,正样本的均值及方差分别为53.22及38.0,样本个数比为0.835.
台风最大风速半径rm为台风中心至台风最大风速的径向距离.由于不能由上海台风研究所获取的台风历史数据直接计算得到台风最大风速半径rm值,此处采用文献[11]分析得到的ln rm与台风中心气压差Δp0的关系进行台风最大风速半径rm的估算,其表达式为
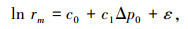
|
(18) |
式中:c0、c1为拟合得到的常系数值;ε为误差项,假定其服从均值0、方差σε的正态分布.对香港地区,经过拟合,可知c0、c1及σε的值分别为5.023 3、-0.024 8及0.458 8.
台风最小距离dmin为研究点至台风移动方向的最小距离,其可根据台风中心位置、研究点位置以及台风移动方向计算得到.此处将利用梯形分布进行香港研究范围内台风最小距离dmin的拟合,其拟合结果见图 1(d).此分布的参数值分别为0、0.002.
2.3 年发生率λ台风年发生率λ为研究点特定范围内每年台风发生的次数.其分布常利用泊松分布来进行拟合.通过对香港地区250 km半径范围内的年台风发生次数进行拟合,可知此地区的台风年发生率λ为2.484.
2.4 台风衰减模型通常采用文献[1]提出的台风衰减模型来表征登陆以后台风强度的衰减状况,其表达式为:
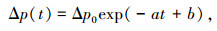
|
(19) |
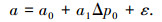
|
(20) |
式中:Δp(t)为登陆t小时后的台风中心气压差,hPa;Δp0为登陆时台风中心气压差,hPa;a为台风衰减系数;b为具有正态分布的随机变量;a0、a1为利用线性拟合法确定的常数;ε为服从零均值正态分布的误差项.
通过对香港地区250 km半径范围内的台风数据资料进行拟合,可知系数a0、a1分别为0.011 1、0.000 2,随机变量b的均值和方差分别为0.018 7、0.129 1,误差项ε的方差为0.018.
3 基于Monte Carlo数值模拟的台风极值风速分析利用Monte Carlo数值模拟方法进行特定地区台风极值风速分析的基本步骤为:1)根据台风历史数据资料,拟合确定台风关键参数概率分布(图 1),并利用Monte Carlo逆变换技术产生进行足够多次数台风风场数值模拟所需的台风关键参数数据库;2)任选一组台风关键参数,根据式(5)求得台风径向气压梯度值,放入台风风场经验模型式(3)、(4)以及(11)、(12)进行风速合成产生初始时刻的台风风场,然后假定台风以不变的移动速度c从海洋移向陆地,根据海岸线坐标计算台风登陆时刻.此后,将台风衰减模型式(19)代入式(5)计算登陆后的台风径向气压梯度值,结合台风风场模型式(3)、(4)以及(11)、(12)分别计算不同时刻登陆以后的台风风场,直至台风完全消失;3)在以上台风发生过程中,同时记录不同时刻研究点处的台风风速、风向数据;4)根据台风年发生率λ,整理得到研究点处的年最大台风风速序列,然后利用文献[12]的台风极值风速分析方法,基于极值Ⅰ型分布,计算得到研究点特定重现期下的极值风速.
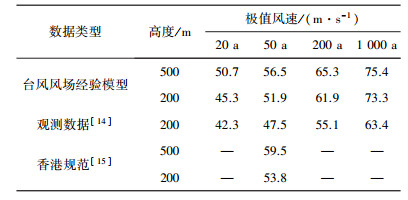
4 台风极值风速分析结果对于台风风场经验模型应用于单次台风风场数值模拟的有效性检验、B的取值范围及讨论,详见文献[13].在台风极值风速预测过程中,利用台风风场经验模型结合拟合得到的台风关键参数概率分布,进行了10 000次台风风场的数值模拟,并记录得到了每次台风发生过程中香港地区的台风风速、风向数据,然后利用极值Ⅰ型分布结合文献[12]的极值风速分析方法,计算得到了20、50、200及1 000 a重现期下香港地区梯度风高度(500 m)以及200 m高度处的台风极值风速,见表 1.计算过程采用的梯度风高度及200 m高度的年最大风速的限值分别为50 m/s及45.5 m/s,上限年最大风速的取值根据蒲福风力等级表给出的台风风速下限值,采用香港风荷载规范的风速剖面推荐指数0.11从10 m高度处分别换算到梯度风高度及200 m高度处计算得到.
| 表 1 香港地区不同重现期下的极值风速 |
文献[14]利用香港横澜岛1983—2006年的台风观测数据,对香港地区20、50、200、1 000 a重现期下的台风极值风速进行了预测,见表 1.另外,根据香港地区的风荷载设计规范[15]计算得到香港地区梯度风高度的极值风速,并根据指数风速剖面指数0.11换算得到了200 m高度处的极值风速,见表 1.
由表 1可看出,香港风荷载设计规范50 a重现期下200 m高度处的极值风速(53.8 m/s)比观测数据的计算结果(47.5 m/s)高约13%,这主要是因为规范在确定香港地区极值风速时,一方面直接采用了1.05的增大系数来考虑风速剖面误差带来的影响,另一方面当时规范计算极值风速时只是依据香港横澜岛1953—1980年的数据进行分析得到,与现有数据计算相比,将会增大计算得到的极值风速误差[14].而文献[14]虽然根据更多的观测数据进行了台风极值风速的计算,但是由于其没有按年最大极值风速序列进行取值计算,而是依照台风风速大于20 m/s的标准进行台风最大风速序列的构建,这将导致计算得到的香港地区不同重现期下的台风极值风速偏小.综合这几方面可知,香港地区的实际台风极值风速值应比表 1给出的观测数据计算结果略大一些,而比现有香港风荷载设计规范小一些更为合理.利用台风风场经验模型进行台风风场模拟数值模拟得到的不同重现期下的香港地区设计风速比观测数据得到的结果要高,其中50 a重现期下的极值风速,比观测数据计算结果高约9%.50 a重现期下,与香港规范给出的极值风速相比,有所降低,约低4%,这正好抵消了香港风荷载设计规范在计算中所考虑的1.05的增大系数.因此,利用台风风场经验模型能模拟得到与香港地区的实际设计风速值比较接近的结果.另外,根据台风风场经验模型计算得到的50 a重现期下香港地区200 m及梯度风高度处的台风极值风速数值模拟结果进行计算可知,其对应的指数风速剖面指数值约为0.1,此值与香港规范推荐的指数风速剖面指数为0.11基本一致,由此可知利用此台风风场经验模型对台风风速剖面进行模拟可以满足要求.
5 结语利用从上海台风研究所获取的1949—2012年的台风历史数据,进行了台风关键参数概率分布的拟合,给出了拟合结果,并提出了基于新的Holland径向气压参数B表达式的台风风场经验模型,然后结合Monte Carlo数值模拟方法完成了香港地区不同重现期下台风极值风速的预测,并与观测数据、香港风荷载规范的结果进行对比分析.分析结果表明,利用台风经验模型计算得到的台风极值风速介于观测数据计算结果与香港风荷载规范推荐值之间,能得到与香港地区实际设计风速比较接近的结果,也可以利用其对台风风速剖面进行较好的描述.
| [1] |
VICKERY P J, TWISDALE L A. Prediction of hurricane wind speeds in the United States[J]. Structural Engineering, 1995, 121(11): 1691-1699. DOI:10.1061/(ASCE)0733-9445(1995)121:11(1691) |
| [2] |
VICKERY P J, SKERLJ P F, STECKLEY A C, et al. Hurricane wind field model for use in hurricane simulations[J]. Structural Engineering, 2000, 126(10): 1203-1221. DOI:10.1061/(ASCE)0733-9445(2000)126:10(1203) |
| [3] |
MENG Y, MATSUI M, HIBI K. A numerical study of the wind field in a typhoon boundary layer[J]. Wind Engineering and Industrial Aerodynamics, 1997, 67/68: 437-448. DOI:10.1016/S0167-6105(97)00092-5 |
| [4] |
VICKERY P J, WADHERA D, POWELL M D, et al. A hurricane boundary layer and wind field model for use in engineering applications[J]. Applied Meteorology and Climatology, 2009, 48: 381-405. DOI:10.1175/2008JAMC1841.1 |
| [5] |
ISHIHARA T, SIANG K K, LEONG C C, et al. Wind field model and mixed probability distribution function for typhoon simulation[C]//The Sixth Asia-Pacific Conference on Wind Engineering. Seoul, Korea: [s. n. ], 2005: 412-426.
|
| [6] |
HOLLAND G J. An analytical model of the wind and pressure profiles in hurricanes[J]. Monthly Weather Review, 1980, 108: 1212-1218. DOI:10.1175/1520-0493(1980)108<1212:AAMOTW>2.0.CO;2 |
| [7] |
HOLLAND G. A revised hurricane pressure-wind model[J]. Monthly Weather Review, 2008, 136: 3432-3445. DOI:10.1175/2008MWR2395.1 |
| [8] |
HOLLAND G J, BELANGER J I, FRITZ A. A revised model for radial profile of Hurricane winds[J]. Monthly Weather Review, 2010, 138: 4393-4401. DOI:10.1175/2010MWR3317.1 |
| [9] |
CARDONE V J, COX A T, GREENWOOD J A, et al. Upgrade of tropical cyclone surface wind field model[R]. Washington: US Army Engineer Waterways Experiment Station, 1992.
|
| [10] |
YING M, ZHANG W, YU H, et al. An overview of the China Meteorological Administration tropical cyclone database[J]. J Atmospheric and Oceanic Technology, 2014, 31: 287-301. DOI:10.1175/JTECH-D-12-00119.1 |
| [11] |
XIAO Yufeng, DUAN Zhongdong, XIAO Yiqing, et al. Typhoon wind hazard analysis for southeast China coastal regions[J]. Structural Safety, 2011, 33: 286-295. DOI:10.1016/j.strusafe.2011.04.003 |
| [12] |
SIMIU E, SCANLAN R H. Wind effects on structures[M]. 3rd ed. New York: John Wiley & Sons, 1996.
|
| [13] |
HUANG Wengfeng, ZOU Kongqing, ZHOU Huanlin. Typhoon wind field simulation with empirical typhoon wind field model for use in engineering applications[C]//The 13th International Symposium on Structural Engineering. Hefei: Science Press, 2014: 1596-1607.
|
| [14] |
HOLMES J D, KWOK K CS, HITCHCOCK P. Extreme wind speeds and wind load factors for Hong Kong[C]//The Seventh Asia Pacific Conference on Wind Engineering. Taipei: [s. n. ], 2009: 801-804.
|
| [15] |
Buildings Department. Code of practice on wind effects in Hong Kong[S]. Hong Kong: Building Department of Hong Kong, 2004.
|
 2016, Vol. 48
2016, Vol. 48