图像修复(image inpainting)是计算机图像处理中的一个热点问题, 是利用当前图像中已知信息对图像中缺损部分按照某种约束实现“合理”填充,使图像恢复完整.该技术主要应用于文物保护和修复、图像/视频编码及传输、游戏设计和电影特效制作等领域.图像修复方法可以分为两类[1]:一类是基于几何结构(geometry-oriented)的方法; 另一类是基于纹理合成(texture-oriented)的方法.其中基于几何结构的方法有文献[2]提出的基于扩散理论的BSCB模型,该方法是沿修复边界的等照度线方向来修复信息损失区域.此外文献[3-4]将图像去噪领域中的TV(total variational)模型、文献[5]将Navier-stokes方程也应用到图像修复领域.总体来说,基于几何结构的模型是通过迭代求解偏微分方程来实现对图像的修复,但是迭代求解偏微分方程时,只利用了缺损区域附近点的几何结构信息和灰度信息,具有很强的局部性,所以该类算法只对图像的小区域缺损(斑点、刮痕、覆盖文字等)具有较好的修复效果;同时由于该类模型对修复区域的光滑性有较强的约束,所以会导致修复区域过于光滑,进而丢失图像待修复区域中的纹理信息,这也局限了该类模型的应用范围.而基于纹理合成方法则是依据一定的准则,在已知图像区域(样本区)搜索最佳匹配像块来填充缺损区域,其中Criminisi算法[6-7]是最成功的算法之一.Criminisi算法利用待修复点邻域的几何结构信息来确定修复优先级,这使得该算法除了具有基于样本块纹理合成技术的修复效率和质量外,还可以保持缺损区域周围的几何结构.文献[8-12]分别对Criminisi算法中的填充修复顺序、优先权计算、置信度更新方式等问题进行了改进.由于对于每一个点的修复都需要在整个样本区中搜索最佳匹配像块,所以该类方法具有很好的全局性,即Criminisi算法对图像缺损较大的区域修复效果较好,但是由于该类算法在图像修复过程中可能利用原本缺损区域中的填充样本来修复缺损区域,所以会导致误差传播,降低图像保持几何结构的能力.由于自然图像中通常同时包含结构部分(图像中的光滑部分和边缘)和纹理部分,所以针对图像缺损区域修复的理想状况是在修复图像结构部分的同时也能够有效地修复区域内的纹理部分[13].基于图像分解的图像修复技术[13-17]首先通过图像分解方法将缺损图像分解为结构部分和纹理部分;然后利用基于偏微分方程模型的方法来修复结构部分、利用纹理合成方法来修复图像的纹理部分;最后通过叠加两部分的修复结果,获得较高质量的修复图像.
但是以上方法在修复时会存在“灰度跳变”和运行复杂度高等问题,所以本文在现有图像修复技术的基础上,提出了一个基于改进TV-H-1模型的改进图像修复方法.该方法首先利用文献[18]的图像分解算法对缺损图像进行分解,获得图像的结构部分和纹理部分; 然后对结构部分和纹理部分分别进行修复:在对结构部分进行修复时,为了解决TV模型在修复图像过程中会产生“灰度跳变”的现象,提出基于偏微分方程(PDEs)和等照度线方向的图像修复方法,记为Isophotes-TV-H-1模型,对结构部分进行修复,同时为了解决Isophotes-TV-H-1模型计算量较大的问题,利用快速行进法(fast march method)对图像缺损区域进行预填充,从而减少迭代次数,提高Isophotes-TV- H-1模型的效率;在进行纹理部分修复时,根据自然图像具有很强局部相似性的特点,对Criminisi算法进行两方面的改进:1)利用局部搜索代替穷尽搜索,进而减少搜索时间,提高算法的效率;2)对Criminisi算法中待修复目标块与参与匹配的样本块之间的相似度进行改进,使得寻找到的最佳匹配块变得更加合理.通过实验对比可知,本文提出的模型相比于TV修复模型、Criminisi算法和基于图像分解的图像修复技术算法[16]具有更好的修复效果.
1 本文模型本文在对传统图像修复算法进行分析后,提出了基于偏微分方程模型(称为Isophote-TV-H-1模型)和改进Criminisi算法的数字图像修复方法.
1.1 图像分解原理对于一幅图形f,一般认为图像可以分解为
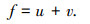
|
式中:u∈BV(Ω)主要包含图像f的低频信息,即结构部分; v∈BV(Ω)包含图像f的高频信息,如图像中的纹理、振荡、噪声部分.针对v部分,在文献[20]中定义了G空间概念,表达式为:
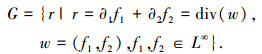
|
因为在H-1(Ω)空间中[19],范数定义为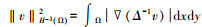
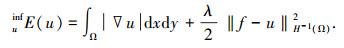
|
(1) |
利用最速下降法求解该能量泛函的最优解,假设u为能量泛函的最优解,w∈BV(Ω), 令u1=(u+εw)∈BV(Ω),那么当ε=0时,u1为式(1)的最优解,对E(u1)关于ε求极值点,可得
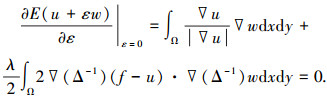
|
(2) |
对式(2)用变分原理及Green公式可变成如下的初边值问题:
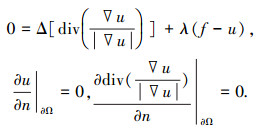
|
(3) |
通过Gauss-Jacobi迭代算法求解式(3)的解,可获得图像的结构部分u.
1.2 结构部分修复算法 1.2.1 基于快速行进法的图像预填充对于结构部分,由于结构部分中只存在光滑区域和边缘,所以结构部分可以视为一个几乎处处连续的函数,根据Taylor展开式定理,I(y)在x点处的展开式为
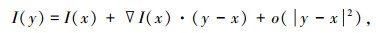
|
舍去高阶项o(|y-x|2)即可以得到如下结果
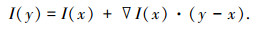
|
(4) |
本文考虑区域填充问题:设P为缺损区域边界上的任意一点,记BεP为P点半径为ε的邻域,那么根据式(4)的Taylor展开式,定义如下的初始值填充算法为
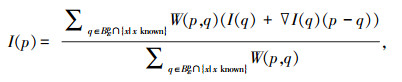
|
(5) |
式中W(p, q)为权重.式(5)的含义为:缺损点P处的初始值为其ε邻域初始值的加权平均.为了保证缺损区域点的初始值按照由边界向内部逐渐延伸顺序,本文借鉴求解水平集函数的快速行进法[21](fast march method).本文算法与文献[21]方法的不同之处:1)文献[21]的更新算法并不能完全保证修复顺序是由边界向内部延伸; 2)本文算法和文献[21]的缺损值估计方法也不相同,在本文中权重W(p, q)主要考虑ε邻域内已知点q处的T(q)的大小,即T(q)越大越接近缺损区域,其权重越大,反之权重越小,它的表达式如
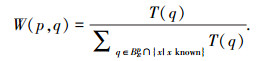
|
基于以上不同,本文对T的更新方法进行了修改,修改后的表达式如
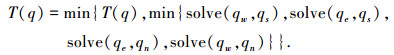
|
式中:qw、qs、qe、qn分别为q的四邻域点, solve(·, ·)用于确定q点处T的可能更新值.
1.2.2 基于改进TV-H-1模型的图像修复分析TV模型对应PDE的数值差分格式,对于缺损区域中的点(i, j),其值的更新是邻域4个点p∈{(i+1, j), (i-1, j), (i, j+1), (i, j-1)}值的加权组合,并且相对应的权值wp分别为
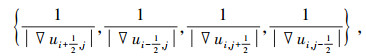
|
即数值同梯度值呈反比,而TV-H-1模型对于缺损区域待修复点(i, j),其值的更新是由其邻域12个点值的加权组合,通过分析可知:由于TV模型只利用其邻域4个点更新中心点信息,而TV-H-1模型利用其邻域12个点的信息来更新中心点,所以TV-H-1模型的修复结果在缺损区域的边界具有更好的连接性,从而缓解了“灰度跳变”现象.对于图像的已知区域,本文希望能够尽量保持不变,但是无论是TV模型还是TV-H-1模型,由于每个点的值都会用周围邻域点来进行加权更新,所以会使图像变得模糊.因此本文对TV-H-1模型进行改进,改进后的表达式为
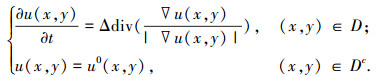
|
(6) |
现对式(6)达到稳定状态的条件进行分析,在传统TV模型式中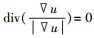
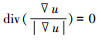
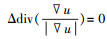
根据文献[3]可以得到式(6)的不动点迭代(fixed-point iteration)离散差分格式为
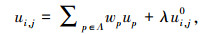
|
把它改写为Gauss-Jacobi迭代形式后的表达式如

|
(7) |
当λ=0时,表达式(7)为式(6)的Gauss-Jacobi迭代格式.
尽管该改进模型能够在解决“灰度跳变”问题的同时保持已知信息,但是该模型中的加权权重只与梯度信息相关,并没有利用等照度线(isophote)的方向信息,所以为了更有效地传播信息,并模拟人工修复图像的工作机制,本文将向量▽Ip与等照度线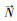
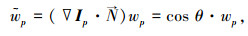
|
式中(▽Ip·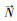
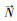
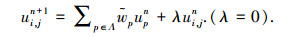
|
(8) |
综上所述,本文提出的Isophote-TV-H-1模型具有以下优点:1)相比于TV模型,利用更多邻域点信息,解决了“灰度跳变”问题;2)能够保持已知区域信息;3)引入等照度线方向信息,模拟人工修复的工作机理,提高信息的传播效率.同时针对Isophote-TV- H-1模型计算量大的问题,本文在对结构部分进行直接修复之前,利用改进的快速行进法对缺损区域值进行预估,这样可以明显减少式(8)的迭代次数.
1.3 纹理部分修复算法 1.3.1 图像局部相似性首先利用统计的方法,对Berkeley大学图像数据库BSDS300中图像的局部相似性进行分析,具体过程如下:
1) 确定块的大小(2pSize+1)×(2pSize+1),在本文实验中pSize = 10;
2) 在每幅图像中随机选择块的中心坐标,记为(x0, y0),确定大小为(2pSize+1)×(2pSize+1)的块patch;
3) 对每一幅原图像、结构图像及纹理图像,取所有可能的大小为(2pSize+1)×(2pSize+1)的图像块Mpatch,Mpatch的中心坐标的距离为(x, y),计算块patch和Mpatch块的Manhattan距离,并计算两个块中心坐标的Euclidean距离Dis;
4) 计算各中心距离为Dis的块patch和Mpatch的平均距离.
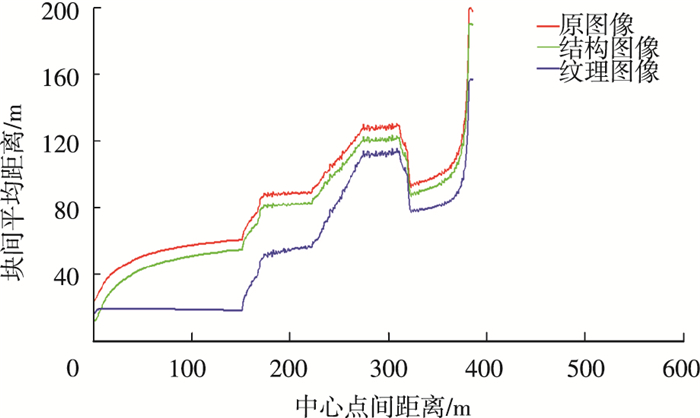
利用上述统计方法,本文统计原图像、结构图像及纹理图像的中心距离-图像块平均距离的关系如图 1所示,对图 1进行分析可以得到如下结论:1)原图像、结构图像和纹理图像的中心距离在0~150时,块间平均距离较小;当超过该距离之后,块间平均距离逐渐增大,这说明自然图像具有很强的局部相似性;2)当3类图像在中心点间距为300~400之间时,块间平均距离有下降的趋势,这说明自然图像不仅具有局部相似性,同时也具有全局冗余,即相似块分布在整幅图像中.对于这两个结果的可能解释是:在获取的自然图像中,存在很多面积较大的物体,同时在同一场景中可能存在多个相似物体,并且每个物体间相隔一段距离.
|
图 1 中心距离-图像块平均距离 |
通过对统计原图像、结构图像及纹理图像的中心距离-图像块平均距离的关系的分析,本文获得图像具有局部相似性的结论,因此对Criminisi算法中的搜索策略进行改进,利用纹理图像的局部相似性,在搜索最佳匹配块时,利用局部搜索方法替代全局搜索,在保证修复效果的前提下提高Criminisi算法的效率.在本文实验中,只在距离缺损区域边界为B(B=30)范围内进行最佳匹配块的搜索.此外,由于马尔可夫随机场模型是纹理图像的一种客观认识,它体现了纹理的局部性和稳定性,即一个像素点或像素块的亮度都可以由它们的邻域像素唯一确定,而与图像的其他部分无关[12].针对Criminisi算法中,每个已知点对相似度的贡献率都是完全相同的情况,本文把其改为与距离相关的加权相似度贡献方式,其相似度定义为
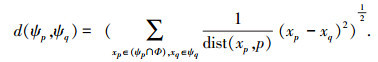
|
式中:dist(xp, p)表示点xp距离中心点p的距离,在本文中距离度量使用Manhattan距离;xp∈(ψp∩Φ)表示xp为ψp中的已知点.相比于Criminisi算法中的相似度,在本文定义的相似度计算中,特征点距离中心点p越近,对相似度的影响越大,否则会变得越小.
2 实验结果本文分别对Lena、Barbara等图像进行图像修复实验,并将实验结果与TV修复模型、Criminisi算法和文献[16]算法的修复结果进行对比.实验结果分别如图 2,3所示,在图 2中,待修复图像(Lena)包含光滑区域,同时也包含丰富的纹理,并且缺损区域1, 4位于光滑区域,缺损区域2, 3位于纹理区域.观察缺损区域2, 3的修复结果,TV模型的修复结果过于光滑,丢失了纹理信息,而Criminisi算法、文献[16]和本文模型较好地修复了缺损区域中的纹理;但是文献[16]的修复结果在缺损区域和已知区域的边界存在比较明显的“灰度跳变”现象,如区域2,同样的现象也出现在缺损区域1.Criminisi算法在区域2和4的修复结果上,由于误差放大,修复区域结果也并不理想,而本文方法则取得了较好的处理结果.对图 3中结果进行分析可得,TV模型对于缺损区域的边缘修复效果较差;而Criminisi算法、文献[16]算法、本文模型对缺损区域内的边缘有更好的修复效果;然而本文模型相比于文献[16]的算法,对缺损区域内的边缘有更强的修复能力;与Criminisi算法相比,尽管Criminisi算法能够较好地修复缺损区域中的边缘和纹理,但是由于误差的传播,该算法在修复缺损区域过程中会引入“新”的边缘;而本文模型则能够较好地控制误差传播,获得较好的修复结果.观察其他图像的处理结果也可以得到同图 2,3所示类似的结论.

|
图 2 Lena对比试验 |

|
图 3 Barbara对比试验 |
为了精确地评价各模型的修复效果,本文分别计算每幅图像修复后的信噪比(signal noise ratio, SNR)和峰值信噪比(peak signal noise ratio, PSNR),SNR和PSNR的定义为
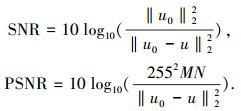
|
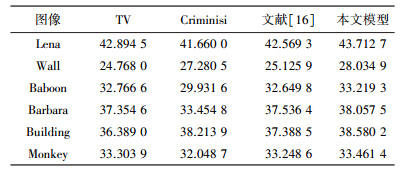
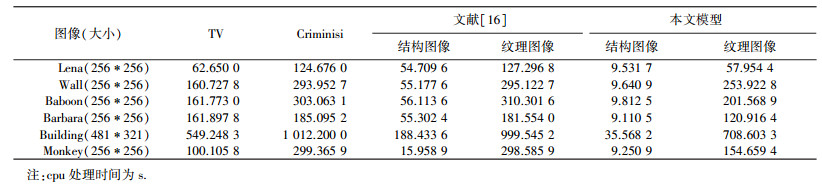
式中:M、N分别为图像的行数和列数;u0、u分别为修复前、后的图像.SNR和PSNR的比较结果见表 1, 2.从表 1, 2中可以看出本文模型具有最高的SNR和PSNR.表 3为TV模型、Criminisi算法、文献[16]算法和本文模型修复图像所用时间的比较,从表 3中可以看出本文的Isophotes-TV-H-1模型在修复纹理图像方面比Criminisi算法更有效率,平均能提高40%,同时本文模型在处理结构图像方面也具有较高的修复效率.
| 表 1 TV模型、Criminisi算法、文献16]、本文模型SNR对比结果 |
| 表 2 TV模型、Criminisi算法、文献[16]、本文模型PSNR对比结果 |
| 表 3 TV模型、Criminisi算法、文献[16]、本文模型修复时间的对比结果 |
1) 通过实验对比可知,与TV模型相比,本文模型能够较好地修复纹理缺损区域中的纹理;与Criminisi算法相比,本文模型通过对相似度度量方法进行改进,能够有效抑制图像修复过程中的误差放大,同时利用局部搜索策略替代Criminisi算法中的穷尽搜索,进而提高算法的处理效率.
2) 通过同文献[16]算法和TV模型的实验对比,可以看出本文方法能够缓解上述算法处理时出现的“灰度跳变”问题,并取得较好的修复结果.
| [1] |
ARIAS P, FACCIOLO G, CASELLES V, et al. A variational framework for exemplar-based image inpainting[J]. International Journal of Computer Vision, 2011, 93(3): 319-347. DOI:10.1007/s11263-010-0418-7 |
| [2] |
BERTALMIO M, SAPIRO G, CASELLES V, et al. Image inpainting[C]//Proceedings of the 27th Annual Conference on Computer Graphics and Interactive Techniques. New York: ACM Press/Addison-Wesley Publishing Co., 2000: 417-424.
|
| [3] |
SHEN Jianhong, CHAN T F. Mathematical models for local non-textureinpaintings[J]. SIAM Journal on Applied Mathematics, 2002, 62(3): 1019-1043. DOI:10.1137/S0036139900368844 |
| [4] |
RUDIN L I, OSHER S, FATEMI E. Nonlinear total variation based noise removal algorithms[J]. Physica D:Nonlinear Phenomena, 1992, 60(1/2/3/4): 259-268. |
| [5] |
BERTALMIO M, BERTOZZI A L, SAPIRO G. Navier-stokes, fluid dynamics, and image and video inpainting[C]//Proceedings of the 2001 IEEE Computer Society Conference on Computer Vision and Pattern Recognition. New York: IEEE, 2001, 1(1): 355-362.
|
| [6] |
CRIMINISI A, PEREZ P, TOYAMA K. Object removal by exemplar-based inpainting[C]//Proceedings 2003 IEEE Computer Society Conference on Computer Vision and Pattern Recognition. New York: IEEE, 2003, 2(2): 721-728.
|
| [7] |
CRIMINISI A, PÉREZ P, TOYAMA K. Region filling and object removal by exemplar-based image inpainting[J]. IEEE Transactions on Image Processing, 2004, 13(9): 1200-1212. DOI:10.1109/TIP.2004.833105 |
| [8] |
SUN Jian, YUAN Lu, JIA Jiaya, et al. Image completion withstructure propagation[J]. ACM Transactions on Graphics, 2005, 24(3): 861-868. DOI:10.1145/1073204 |
| [9] |
翟东海, 肖杰, 鱼江, 等. 基于自适应模板的图像修复算法[J]. 计算机应用, 2013, 33(10): 2891-2894. DOI:10.3969/j.issn.1001-3695.2013.10.003 |
| [10] |
王梅, 赵彩, 郭勇. 基于重构样本区域的数字图像修复算法研究[J]. 软件导刊, 2014, 13(2): 71-73. |
| [11] |
张巧焕, 唐向宏, 任澍. 区域自适应的图像修复算法[J]. 计算机工程与应用, 2013, 49(21): 160-163, 171. DOI:10.3778/j.issn.1002-8331.1201-0216 |
| [12] |
张申华, 王克刚, 祝轩. 局部特征信息约束的改进Criminisi算法[J]. 计算机工程与应用, 2014, 50(8): 127-130. |
| [13] |
贾渊, 刘鹏程, 牛四杰. 偏微分方程图像处理及程序设计[M]. 北京: 科学出版社, 2012: 160-176.
|
| [14] |
STARCK J L, ELAD M, DONOHO D L. Image decomposition via the combination of sparse representations and a variational approach[J]. IEEE Transactions on Image Processing, 2005, 14(10): 1570-1582. DOI:10.1109/TIP.2005.852206 |
| [15] |
沈民奋, 陈家亮, 代龙泉, 等. 基于图像分解和图像分割的数字图像修复[J]. 电子测量与仪器学报, 2009, 23(9): 11-17. |
| [16] |
林云莉, 赵俊红, 朱雪峰, 等. 基于图像分解的图像复原技术[J]. 计算机工程, 2010, 36(10): 187-192. |
| [17] |
王阿川, 侯畅, 宋宏光, 等. 基于图像分解的单板节子缺陷图像修补方法研究[J]. 林业机械与木工设备, 2013, 41(8): 50-54. |
| [18] |
OSHER S, SOLÉ A, VESE L. Image decomposition and restoration using total variation minimization and the H-1 norm[J]. Multiscale Modeling & Simulation, 2003, 1(3): 349-370. |
| [19] |
MEYER Y. Oscillating patterns in image processing and nonlinear evolution equations:the fifteenth Dean Jacqueline B. Lewis memorial lectures[M]. New York: American Mathematical Society, 2011.
|
| [20] |
VESE L A, OSHER S J. Modeling textures with total variation minimization and oscillating patterns in image processing[J]. Journal of Scientific Computing, 2003, 19(1): 553-572. |
| [21] |
TELEA A. An image inpainting technique based on the fast marching method[J]. Journal of Graphics Tools, 2004, 9(1): 23-24. DOI:10.1080/10867651.2004.10487596 |
| [22] |
徐晨, 李敏, 张维强, 等. 后小波与变分理论及其在图像修复中的应用[M]. 北京: 科学出版社, 2013: 183-184.
|
| [23] |
CHAN T F, SHEN Jianhong. Non-textureinpainting by curvature-driven diffusions[J]. Journal of Visual Communication and Image Representation, 2001, 12(4): 436-449. DOI:10.1006/jvci.2001.0487 |
 2016, Vol. 48
2016, Vol. 48