直升机阵风载荷是指直升机在遭遇阵风时机体质心处过载系数的变化,是直升机结构设计和强度计算的重要依据[1].直升机在低空飞行遭遇阵风时,旋翼处风场的变化会导致较大的瞬态载荷和动应力,影响直升机动部件的疲劳评定和设计[2].因此,精确计算直升机在变化风场中的阵风载荷直接影响直升机的结构质量、性能和安全.
直升机由于其结构的特殊性、气动的复杂性以及各通道耦合的严重性,在风场中的载荷变化非常复杂.目前,国内外关于直升机风场中飞行特性和抗风策略等方面的研究多是基于小扰动线性化动力学模型[3-5],采用逐步求解法可以确定各部件气动力的变化,进而进行阵风载荷分析[6].在许多情况下,线性化或常系数近似法是不合适的[7],且基于小扰动模型设计的控制律对实际直升机的控制系统设计帮助有限[8].随着理论和计算手段的发展,直升机非线性飞行动力学模型的研究越来越得到重视[9-13].目前,关于直升机非线性系统的风场响应研究也越来越多[14-17],这些研究均未考虑飞机在进入风场时刻风场的突变所导致的变化风场时间导数对直升机性能参数响应结果的影响.本文基于此发展了变化风场中直升机非线性动力学模型,通过直升机过载系数的时域响应分析计算阵风载荷,探讨前进比、阵风方向和阵风强度等参数对阵风载荷的影响.
1 变化风场中直升机动力学模型 1.1 直升机非线性系统文献[13]建立了一种常规单旋翼带尾桨直升机飞行动力学的非线性系统,综合考虑旋翼、尾桨、机身、垂直安定面和水平安定面气动力素,并以UH-60直升机为对象,通过配平仿真计算结果与文献[18]中的试飞数据对比验证了该模型的精度.其机体的质心运动方程为:
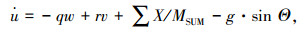
|
(1) |
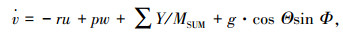
|
(2) |
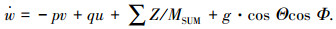
|
(3) |
机体绕质心转动的动力学方程为:
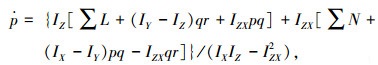
|
(4) |
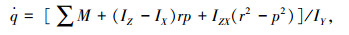
|
(5) |
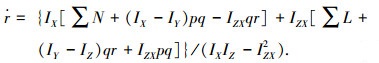
|
(6) |
姿态角与角速度的几何关系为:
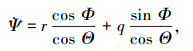
|
(7) |
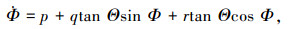
|
(8) |
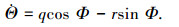
|
(9) |
式(1)~式(9)均是在机体坐标系下.其中:MSUM为全机质量;∑X、∑Y、∑Z分别为质心处所受合外力在体轴上的分量;∑L、∑M、∑N分别为质心处所受合外力矩在体轴上的分量;IX、IY、IZ分别为机体3个轴方向的惯性矩;IZX为惯性积;g为重力加速度;u、v、w分别为质心速度在机体坐标系上的分量;p、q、r分别为机体的角速度在机体坐标系上的投影,分别称为滚转角速度、俯仰角速度和偏航角速度;Θ、Φ、Ψ分别为机体相对地面坐标系俯仰角、滚转角和偏航角.
1.2 变化风场中质心运动方程直升机进入风场后,地速VG、空速VA和风速VW构成速度三角形,有
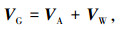
|
(10) |
其中地速VG即直升机飞行速度.考虑到直升机各部件的气动力素均是由空速决定,因此需要建立变化风场中的机体质心运动方程.
机体坐标系obxbybzb下(以下标“b”表示该机体),根据牛顿运动第二定律为
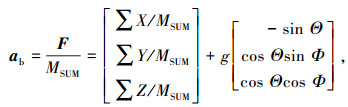
|
(11) |
式中ab为机体系下加速度矢量,且为质心地速对时间的导数,则有
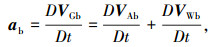
|
(12) |
其中:空速矢量的时间导数为
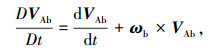
|
(13) |
风速矢量的时间导数为
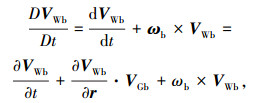
|
(14) |
式中:
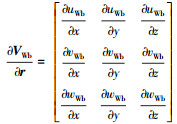
将式(12)~(14)代入到式(11)中,可以得到变化风场中的质心运动方程为
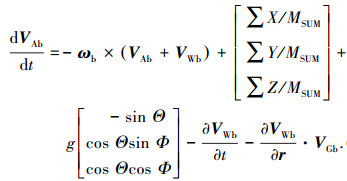
|
(15) |
其标量形式如下:
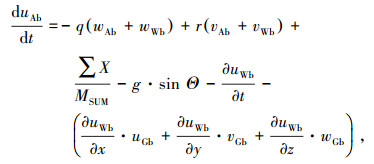
|
(16) |
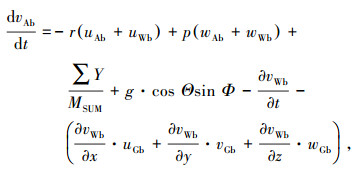
|
(17) |
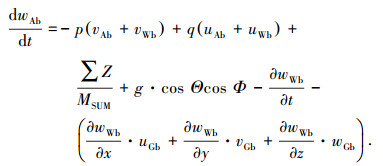
|
(18) |
式中:uAb、vAb、wAb分别为质心处空速在机体坐标系上的分量;uGb、vGb、wGb分别为质心处地速在机体坐标系上的分量.
1.3 变化风场中直升机动力学模型将式(4)~(9),(16)~(18)和文献[13]中旋翼挥舞动力学方程、尾桨动力学方程以及动力入流方程联立就构成了变化风场中直升机动力学模型,可以整理如下形式
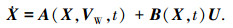
|
(19) |
式中:X为状态向量, U为控制向量, VW为直升机质心在当前位置和时刻的风速矢量.
式(19)为一阶非线性微分方程,配平后可以通过四阶龙格-库塔法进行求解,实现直升机在变化风场中的时域响应分析.
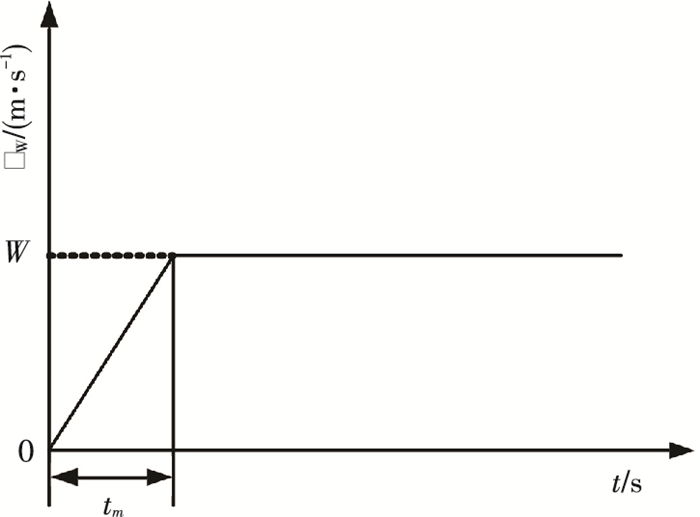
2 阵风载荷计算 2.1 阵风模型阵风作为最常见的风场形式,可表征离散的风切变、大气紊流的峰值、飞机尾流区域流动、地形诱导的气流等[19].阵风模型一般根据实测资料统计确定,可以分为阶跃、斜坡、三角形、正弦形和正弦平方形等几种类型[20].根据文献[1, 6],在实际应用中,较多采用斜坡形阵风,阵风模型如图 1所示.
|
图 1 斜坡形阵风模型 |
图 1中,tm=Lgust/V0.其中,V0为直升机进入风场时的飞行速度,Lgust为阵风梯度距离,即阵风速度由零到阵风速度最大值W的距离,鉴于各国规定不同,其中俄罗斯取Lgust=2R(R为直升机旋翼半径),美国取Lgust=27.432 m,英国取Lgust=30.48 m,中国取Lgust=30 m.故本文取tm=30/V0.当高度增加时,阵风速度最大值W计算为
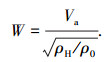
|
(20) |
式中:Va为阵风强度;ρH为直升机所在飞行高度的空气密度;ρ0为地面空气密度.
2.2 阵风载荷直升机过载系数一般指在直升机质心处的垂直方向过载,它是直升机各部件在质心处沿旋翼桨毂方向的合力与直升机重力之比,即
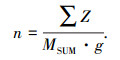
|
(21) |
其中

|
MR、TR、F、VS、HS分别为旋翼、尾桨、机身、垂直安定面和水平安定面.
直升机在飞行过程中遭遇水平阵风或垂直阵风时,对于刚性飞机,阵风载荷分析一般只关注响应过程中质心处过载系数的极值,即最大过载系数和最小过载系数.因此,可以通过直升机过载系数的时域响应分析得到阵风载荷.
2.3 工程估算除了采用以上所述的飞行动力学模型计算阵风载荷外,根据《直升机载荷手册》[6],在工程应用中,对于低速和中速前飞阶段,可以采用估算公式[21]计算垂直阵风载荷
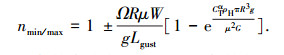
|
(22) |
式中:Ω为旋翼旋转角速度; R为旋翼半径; μ=uK/(ΩR)为直升机前进比; uK为直升机前飞速度分量; g为重力加速度; G为直升机飞行重力; CTα为拉力系数对迎角的导数.
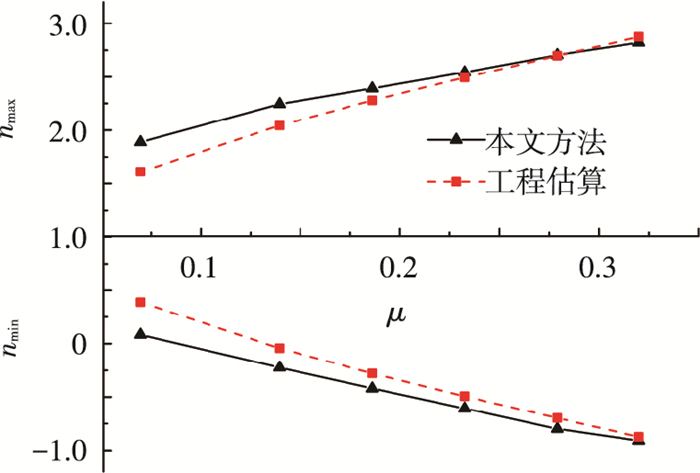
3 模型验证本文分别采用变化风场直升机过载系数和估算公式计算阵风载荷,通过结果对比验证模型的正确性.以国内某型号直升机为例,直升机飞行质量5 250 kg,旋翼转速31.85 rad/s,旋翼半径6.75 m.假定直升机飞行高度1 600 m,在2 s时刻遭遇垂直向上和垂直向下方向的阵风,阵风强度Va=10 m/s.图 2为直升机在不同前进比下阵风载荷计算结果.
|
图 2 阵风载荷计算结果对比 |
图 2中可以看出,在小前进比时,本文计算最大过载系数略大于估算公式结果,最小过载系数略小于估算公式结果.这是因为估算公式仅考虑主旋翼对阵风载荷的影响,而在实际飞行过程中,尾桨、机身、垂直安定面和水平安定面等部位产生的升力对过载系数都有影响,导致两者计算结果出现差别.随着前进比的增大,直升机过载更多由主旋翼贡献,两种方法的计算结果越来越接近.因此本文所采用的直升机非线性模型综合考虑了直升机各部件所产生的升力,所建立的变化风场中直升机非线性动力学模型能够精确计算不同前进比时的阵风载荷,可以用于直升机预研阶段阵风载荷分析.
4 直升机阵风载荷分析 4.1 变化风场时间导数对阵风载荷的影响假定直升机在1 600 m高度做定速平飞,以3种前进比(0.07、0.19、0.32),在2 s时刻遭遇垂直向上方向阵风,阵风强度Va=10 m/s.图 3为分别考虑时间导数和不考虑时间导数情况下过载系数时域响应分析结果.

|
图 3 考虑和不考虑时间导数过载系数时域响应结果对比 |
图 3的对比结果可以看出,无论直升机飞行速度的高低,直升机在遭遇阵风的瞬间,风速的突变会在短时间内产生很大的时间导数,造成过载系数响应幅值的增大,对阵风载荷分析结果的影响较大.因此,在阵风载荷分析时考虑时间导数的影响是必要的.
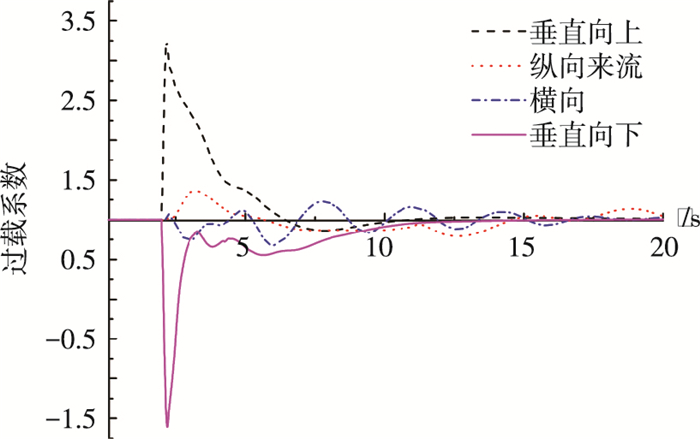
4.2 阵风方向对阵风载荷的影响假定直升机做定速平飞,前行速度为178 km/h(μ=0.23),飞行高度1 600 m,在2 s时分别遭受垂直向上、纵向来流、横向和垂直向下4个方向的斜坡阵风,阵风强度Va=15 m/s.图 4为不同方向对应的阵风过载系数时域响应计算结果.
|
图 4 不同方向阵风过载系数时域响应 |
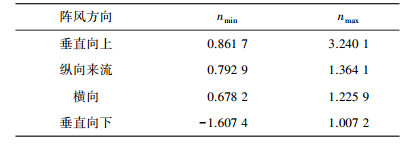
通过图 4的域响应结果,就可以得到直升机响应过程中的最大过载系数和最小过载系数.表 1为不同阵风方向对应的最大过载系数和最小过载系数.
| 表 1 不同方向阵风载荷计算结果 |
表 1可以看出,垂直向上的阵风会造成过载系数瞬时大幅增大,在趋于平稳的过程中过载系数只会略小于1,因此阵风载荷分析只需考虑最大过载系数;垂直向下的阵风会使过载系数瞬时大幅减小,在响应过程中只会造成过载系数略大于1,因此阵风载荷分析只需考虑最小过载系数;对于横向和纵向的水平阵风,过载系数变化比较平稳且振动幅度很小,可以认为水平方向的阵风载荷对直升机结构强度影响很小,所以本文只进行垂直方向阵风载荷分析.
4.3 前进比和阵风强度对阵风载荷的影响根据《军用直升机强度和刚度规范》[22],直升机从悬停到Vmax的每个临界空速下,应能承受15 m/s(民用直升机为9.14 m/s)的垂直和水平阵风所产生的载荷.本文假定直升机在1 600 m高空,以3种前进比(μ=0.14、0.23、0.32)进入阵风风场,阵风强度范围为-15~15 m/s,规定阵风方向垂直向下时为正.图 5为不同前进比和阵风强度下对应的过载系数极值.

|
图 5 直升机前飞时垂直阵风载荷计算结果 |
图 5可以看出,在同一前进比下,当直升机遭遇垂直向上阵风时,阵风载荷为最小过载系数,随着阵风强度的增强而近似于线性减小;当直升机遭遇垂直向下阵风时,阵风载荷为最大过载系数,随着阵风强度的增强而近似于线性增大.在同一阵风强度下,当直升机遭遇垂直向上阵风时,直升机的前进比越大,阵风载荷就越大;当直升机遭遇垂直向下阵风时,直升机的前进比越大,阵风载荷就越小, 而且阵风载荷随直升机前飞速度变化的敏感性(斜率)随阵风强度的增强而不断增大.此外可以看到,在同一前进比下,阵风载荷与阵风强度之间有近似线性关系,这与估算公式非常吻合,进一步验证了模型的正确性.
本文所采用的直升机过载系数的设计范围为-1.0~+3.5,可以根据图 5的阵风载荷分析结果估算直升机在不同前进比下所能承受的最大阵风强度.
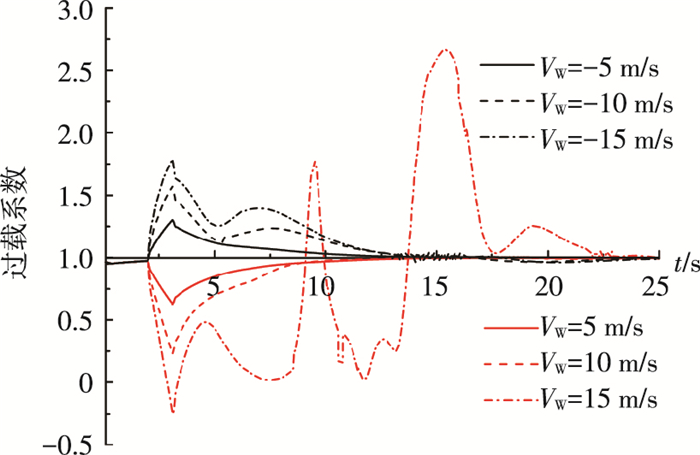
4.4 直升机爬升状态下阵风载荷分析本文分析方法还适用于直升机其他飞行状态下阵风过载系数时域响应分析,图 6为直升机在500 m高空以7.5 m/s速度爬升时,遭遇不同强度和方向阵风时过载系数时域响应,阵风方向垂直向下时为正.
|
图 6 直升机爬升阶段过载系数时域响应 |
图 6可以看出,直升机爬升时遭遇垂直向上方向阵风时,随着阵风强度的增强阵风载荷略有增大,直升机也很快可以恢复到稳定飞行状态; 直升机遭遇垂直向下方向阵风时,阵风强度的增大也会造成过载系数振动幅度增大.当阵风强度达到15 m/s时,阵风载荷最大达到2.667 5,虽然没有超过结构强度设计范围过载系数,但从响应过程可以明显看出过载系数出现无规律的大范围波动情况,直升机飞行状态发生异常.这是因为在遭遇垂直向下阵风时,过载系数会瞬时降低,为了使直升机恢复稳态飞行,需要加大直升机总距操纵,提高直升机旋翼拉力,使直升机恢复稳定飞行状态.但是随着阵风强度的增强,当所需调整的总距操纵超过直升机可以提供的操纵极限,直升机将无法恢复稳定状态,各状态参数出现大范围的波动,直升机出现失稳现象.所以垂直向下方向的阵风对直升机爬升时的危害更大,直升机在飞行时应尽力回避高强度垂直向下方向阵风.
5 结论1) 直升机在遭遇阵风的瞬间由于风速突变所产生的时间导数对过载系数响应结果影响较大,在阵风载荷分析时需要考虑变化风场时间导数的影响.
2) 全面考虑直升机机翼、尾翼、机身、垂直安定面和水平安定面等各部件力素对载荷的影响,能够精确计算不同前进比时的阵风载荷,尤其在小前进时,相比工程估算公式具有更高的精度.
3) 简单的通过阵风载荷判断阵风对直升机飞行的影响不够准确,只有通过过载系数时域响应分析,可以更加直观全面的反映直升机飞行状态,为直升机结构设计和抗风飞行策略研究提供可靠详实的参数数据.
| [1] |
飞机设计手册编委会. 飞机设计手册-直升机设计[M]. 北京: 航空工业出版社, 2005.
|
| [2] |
萧秋庭. 直升机旋翼阵风响应研究[J]. 飞行力学, 1994, 12(4): 8-13. |
| [3] |
PADFIELD G D. Helicopter flight dynamics[M]. New York: John Wiley & Sons, 2008.
|
| [4] |
高华. 风切变对直升机飞行特性的影响[D]. 南京: 南京航空航天大学, 2009.
|
| [5] |
王刚强. 大气扰动下无人直升机悬停/小速度段位置控制律设计[D]. 南京: 南京航空航天大学, 2009.
|
| [6] |
航空航天工业部科学技术研究院. 直升机载荷手册[M]. 北京: 航空工业出版社, 1991.
|
| [7] |
ELLIOTT A S, CHOPRA I. Helicopter response to atmospheric turbulence in forward flight[J]. Journal of the American Helicopter Society, 1990, 35(2): 51-59. DOI:10.4050/JAHS.35.51 |
| [8] |
刘家宁, 陆宇平. 直升机的精确建模与仿真控制研究[J]. 飞机设计, 2007, 27(2): 29-33. |
| [9] |
CHEN R T N. A Simplified rotor system mathematical model for piloted flight dynamics simulation, NASA TM-78575[R]. Washington, DC: NASA, 1979.
|
| [10] |
HOWLETT J J. UH-60A black hawk engineering simulation program, NASA CR-166309[R]. Washington, DC: NASA, 1981.
|
| [11] |
BALLIN M G. . Validation of a real-time engineering simulation of the UH-60A helicopter[R]. Washington, DC: NASA TM-88360, 1987.
|
| [12] |
KIMF D, CELI R, TISCHLER M B. High-order state space simulation models of helicopter flight mechanics[J]. Journal of the American Helicopter Society, 1993, 38(4): 16-27. DOI:10.4050/JAHS.38.16 |
| [13] |
杨超. 直升机飞行动力学仿射非线性系统建模与验证[D]. 北京: 北京航空航天大学, 1995.
|
| [14] |
余江. 直升机飞行动力学仿真和大气紊流响应的研究[D]. 北京: 北京航空航天大学, 1995.
|
| [15] |
洪冠新, 庞健. 风切变场中直升机前飞状态动态响应[J]. 北京航空航天大学学报, 2005, 31(5): 524-528. |
| [16] |
MARTINI A, LEONARD F, ABBA G. Robust nonlinear control and stability analysis of a 7DOF model-scale helicopter under vertical wind gust[C]//IEEE/RSJ International Conference on. Intelligent Robots and Systems. Nice: IEEE Press, 2008: 354-359.
|
| [17] |
吉洪蕾, 陈仁良, 李攀. 适用于直升机飞行力学分析的三维空间大气紊流模型[J]. 航空学报, 2014, 35(7): 1825-1835. |
| [18] |
BALLIN M G. Validation of a real-time engineering simulation of the UH-60A helicopter[R]. Washington, DC: NASA TM-88360, 1987.
|
| [19] |
肖业伦, 金长江. 大气扰动中的飞行原理[M]. 北京: 国防工业出版社, 1993.
|
| [20] |
DREESJ M, HARVEY K W. Helicopter gust response at high forward speed[J]. Journal of Aircraft, 1970, 7(3): 225-230. DOI:10.2514/3.44150 |
| [21] |
张雅铭. 直升机突风载荷计算[J]. 直升机技术, 1979, 1-2. |
| [22] |
国防科学技术工业委员会. GJB720. 2-89军用直升机强度和刚度规范[S]. 北京: 航空工业出版社, 1989.
|
 2016, Vol. 48
2016, Vol. 48