2. 中国船舶重工集团公司第七一一研究所, 201108 上海
2. Shanghai Marine Diesel Engine Research Institute, 201108 Shanghai, China
舰船在水下爆炸载荷作用下,船体的响应会对内部设备和管路产生冲击,如何复制管路的冲击破损影响舰船生命力[1],是目前舰船抗冲击研究的重要领域.国外对舰船管路抗冲击研究较为重视,并开展大量理论和试验研究[2],但是国内针对管路系统的研究还不够深入和广泛.研究方法主要基于理论推导和有限元仿真计算[3],鲜有试验研究[4].随着计算机技术的迅猛发展和数值计算能力的不断增强,数值仿真技术日益受到重视[5].但是有限元仿真从建模到计算,都需要投入大量的人力、物力,模型修改过程繁琐,且精度与单元网格的划分密切相关.而离散时间传递矩阵方法模型修改灵活、易于编程并且具有较高的计算精度.传统的传递矩阵方法能较好的解决线性或者低频问题,但并不适合处理冲击等非线性领域问题.为解决复杂的非线性动力学问题,文献[6-8]提出了离散时间传递矩阵法.本文应用精细传递矩阵方法,编制舰船管路冲击响应计算程序,形成舰船管路冲击响应的计算方法,设计试验对本文提出的计算方法进行验证,并与有限元计算结果进行了对比.
1 离散时间精细传递矩阵法 1.1 动力学方程Timoshenko梁横向振动微分方程组

|
(1) |
式中:G为剪切模量; y为挠度; θ为转角; M为弯矩; rs为回转半径; N为剪力; ρ为密度; ks为系数; A为截面积; E、I分别为弹性模量和惯性矩; f(x, t)外载荷.
令Z=[y θ M N 1]T表示节点状态矢量,则式(1)写成矩阵的形式可以表示为
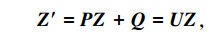
|
此时,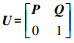
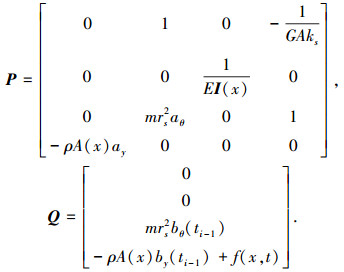
|
不同于传统传递矩阵法,而离散时间精细传递矩阵法采用离散的方法,将梁等分成不同的节点,n表示分段数量,形式如图 1所示.

|
图 1 精细传递矩阵方法分段图 |
由于冲击波速度大而管路较短,忽略冲击波的传播时间.通过杜哈曼积分,ti时刻,解式(1)得到[9]
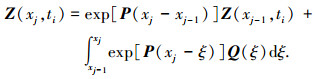
|
(2) |
式(2)等号右边第1项为矩阵指数,等号右边第2项为杜哈曼积分项.对于式(2)等号右边第1项采用精细积分方法计算[10].
令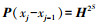

|
(3) |
对exp(H)进行Taylor展开,得到
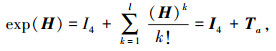
|
(4) |
将式(3)代入式(4),得到
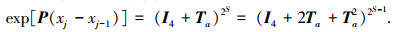
|
在数值实现过程中,将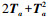
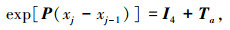
|
这样便实现了矩阵指数的求解,并且在编程计算中,能够减小误差[11-12].
式(2)为离散时间传递矩阵在节点i处的方程,可以得到总系统方程:
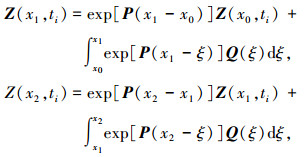
|
(5) |
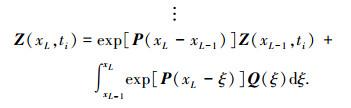
|
通过上述传递可以得到系统首尾的关系如下
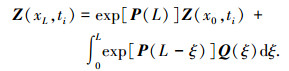
|
(6) |
根据初始边界条件,可以求得半数物理量.余下的物理量由式(6)得到,确定系统两个边界的物理量,通过式(5)的传递关系进而求得同一时间的各离散点的物理量.根据得到的物理量计算相邻时间节点的物理量,通过上述推导即可求解管路在冲击载荷作用下的响应.
2 试验验证为验证本文提出的数值计算方法的准确性,设计了管路冲击试验进行验证,将计算结果与试验值进行了对比.综合考虑试验台测试能力,选用管径DN25管路,外径30 mm,管壁2 mm,密度8 940 kg/m3,泊松比0.3,弹性模量1.4 e11.
采用提出的管路冲击响应计算程序,对多跨直管和三通管路的冲击响应就行求解,并将计算结果与试验测点数据进行对比.图 2为直管内封闭有水的试验模型,图 3为应变片及加速度传感器安装图,加速度传感器安装于设计的传感器支座上.

|
图 2 充液多跨直管冲击试验模型 |

|
图 3 测量管路上加速度和应变片 |
图 4中TMM表示传递矩阵法计算得到的曲线(以下相同),从三通管路的加速度曲线对比可以看出,离散时间精细传递矩阵法计算结果与试验值对比具有较好的精度,加速度和应力峰值计算结果与试验值误差较小.图 5曲线表明应力响应误差较小,冲击响应幅值和频率吻合良好.误差产生的原因可能是边界条件的简化,以及载荷与真实值有一定的差别.但是数值计算结果和试验测试结果总体上误差较小,见表 1.

|
图 4 三通管路测点加速度曲线 |

|
图 5 三通处上表面单元应力曲线 |
| 表 1 加速度峰值 |
表 1结果表明,本文提出的方法既保证了较高的计算精度,同时计算时间大为降低,效率明显提高,相对误差小于20%,可能是计算所用载荷为冲击机平台上传感器测量值,这与试验中管路支点承受的冲击有一定的误差.所以,如果去除这部分误差,离散时间精细传递矩阵方法的精度将会更高.
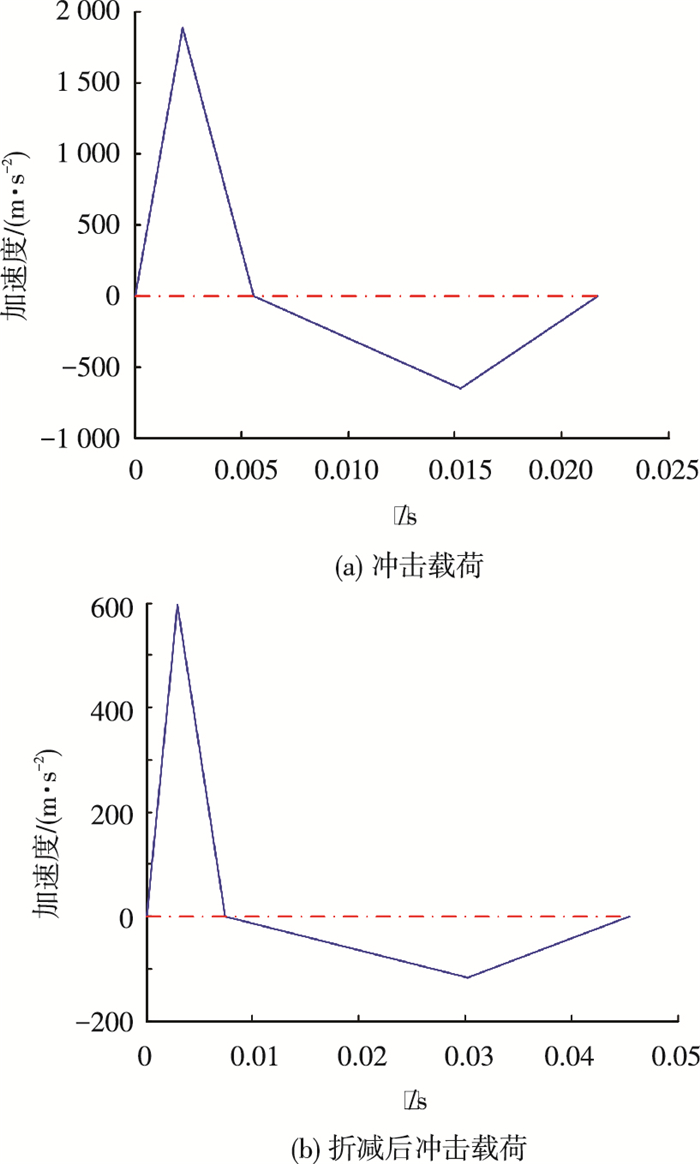
3 计算结果对比 3.1 载荷及边界条件根据BV043/85规范[12]的设备冲击校核准则将冲击谱转换成时域载荷,基座处的冲击载荷需要按规范进行折减,以此作为基础激励冲击加速度,得到的冲击载荷如图 6所示.将换算得到的载荷作为边界条件分别施加到管路的基座底部(支撑处),管路端部采用自由端边界条件,不施加载荷和约束.
|
图 6 正负三角波载荷 |
本文选择弯头管路和三通管路作为算例,应用离散时间精细传递矩阵法,编制Matlab三维管路冲击响应程序,对弯头和三通管路进行冲击响应分析.离散时间精细传递矩阵法和有限元方法采用相同的管路模型,支撑刚度均为5e5 N/m.并结合ANSYS、HyperMesh和ABAQUS等软件建立船体结构有限元模型,施加同样的边界条件和载荷,计算管路的冲击响应,与离散时间精细传递矩阵方法进行对比.
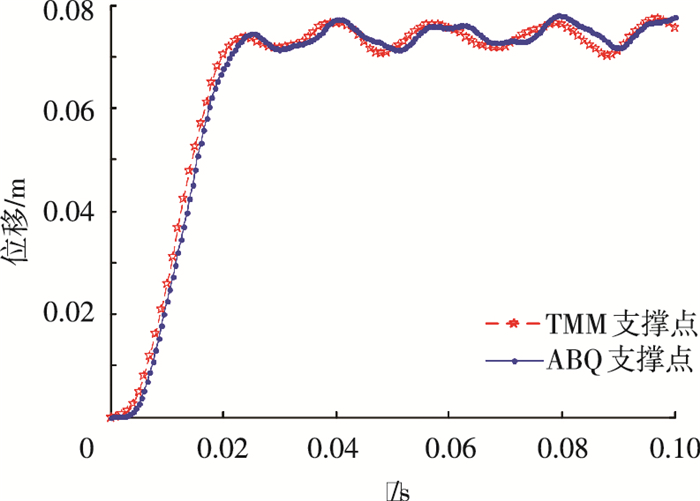
3.2.1 弯头管路冲击响应数值计算结果对比离散精细传递矩阵计算程序用时96.8 s,图 7, 8分别是自编程序与ABAQUS软件计算结果得到的支撑点处和右端位移曲线对比.ABQ表示有限元计算结果(以下相同).离散时间精细传递矩阵自编程序与ABAQUS软件计算结果吻合很好,弹簧支撑点位移曲线峰值误差小于1%,右端点位移曲线峰值小于5%.
|
图 7 弹簧支撑点位移曲线对比 |
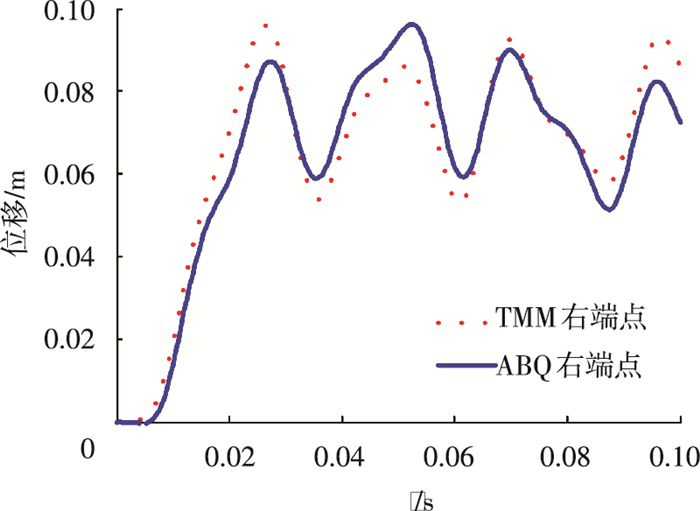
|
图 8 右端点位移曲线对比 |
图 9为t=40 ms时离散时间精细传递矩阵法与有限元方法计算得到的三通管路变形对比图,可以看出两种计算方法得到的管路变形基本一致.离散精细传递矩阵计算程序用时76.8 s.有限元方法建模及计算需要耗费的时间较长,通常需要耗费数小时的时间;精细传递矩阵方法自编程序仅需要设定管路节点坐标位置和材料属性就可以实现相应分析,完成完整的计算仅需要几分钟的时间,耗时要远远小于有限元方法计算所需时间.

|
图 9 两种方法计算结果对比 |
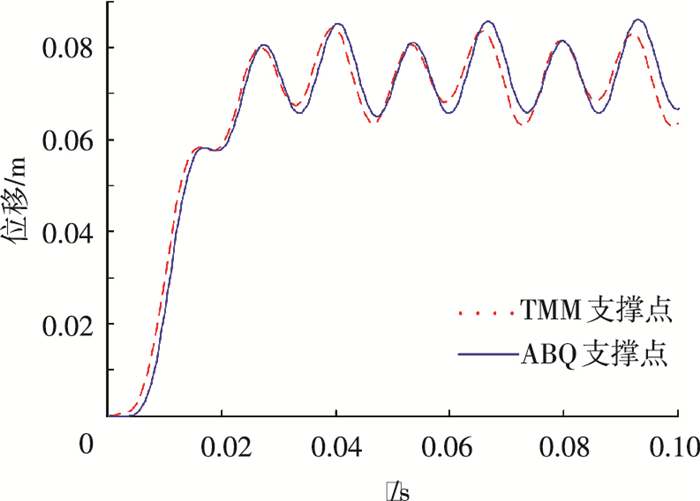
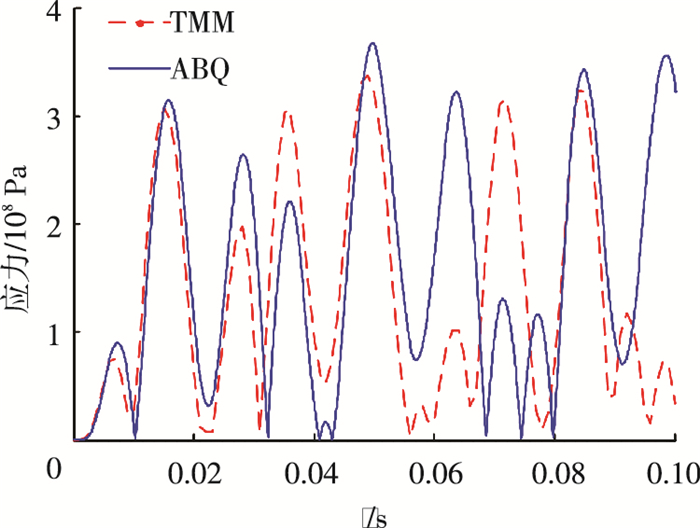
图 10, 11分别是本文计算方法与有限元方法得到的三通处位移曲线和应力曲线计算结果.离散时间精细传递矩阵法计算结果与有限元对比精度较高,位移和应力峰值计算结果误差较小.对于应力曲线,计算前期两种方法之间的误差较小,但在后期出现了一定的差别.原因可能是自编程序在矩阵连乘中,由于计算机的精度导致的舍入误差,误差经过积累逐步放大,造成应力曲线后期的峰值误差,并且有限元计算方法与离散时间传递矩阵方法所选取的时间步长不同,在对时间积分时,由于累积误差,可能造成应力曲线后期出现了一定的相位差,而且有限元软件计算结果与真实值相比也存在误差,这也可能导致两种方法存在一定的差别.
|
图 10 三通处位移曲线对比 |
|
图 11 三通处Mises应力曲线对比 |
表 2为两种方法在管路支撑点和三通处位移曲线前3个波峰值的对比结果.两种计算方法得到的位移前3个周期的峰值最大相对误差仅为1.2%,最小误差只有0.2%,通过上述结果可以看出,本文提出的计算方法与有限元方法计算管路冲击位移和应力响应结果基本一致,自编程序能够准确高效的模拟舰船管路冲击响应.
| 表 2 位移计算结果 |
1) 设计了管路冲击试验,利用试验数据对本文提出的计算方法的有效性进行验证,离散时间传递矩阵法计算得到的直管和三通管路冲击加速度误差分别为18.8%和19.1%,精度较好,并且响应周期较为稳定.
2) 精细传递矩阵方法计算典型管路的冲击响应与有限元方法计算结果进行对比,发现本文提出的数值计算方法精度良好.对于弯头管路,离散时间精细传递矩阵自编程序与ABAQUS软件计算结果吻合很好,弹簧支撑点位移曲线峰值误差小于1%,右端点位移曲线峰值小于5%.对于三通管路,两种计算方法得到的位移峰值最大相对误差仅为1.2%,最小误差只有0.3%,吻合良好,应力曲线误差也较小.
3) 相对于有限元方法需要进行前期建模、网格划分等过程,离散时间精细传递矩阵方法自编程序建模更为便捷,相对于有限元方法,计算时间大幅缩短.
| [1] |
YANG J L, LU G Y, YU T X, et al. Experimental study and numerical simulation of pipe-on-pipe impact[J]. International Journal of Impact Engineering, 2009, 36(10/11): 1259-1268. |
| [2] |
LIANG C C, TAI Y S. Shock responses of a surface ship subjected to noncontact underwater explosions[J]. Ocean Engineering, 2006, 33(5/6): 748-772. |
| [3] |
XU Guofu, DENG Zhengdong, DENG Feifan, et al. Numerical simulation on the dynamic response of buried pipelines subjected to blast loads[J]. Advanced Materials Research, 2013, 671-674: 519-522. DOI:10.4028/www.scientific.net/AMR.671-674 |
| [4] |
SHAH Q H. Experimental and numerical study on the orthogonal and oblique impact on water filled pipes[J]. International Journal of Impact Engineering, 2011, 38(5): 330-338. DOI:10.1016/j.ijimpeng.2010.12.001 |
| [5] |
MATHAN G, PRASAD N S. Study of dynamic response of piping system with gasketed flanged joints using finite element analysis[J]. International Journal of Pressure Vessels and Piping, 2012, 89: 28-32. DOI:10.1016/j.ijpvp.2011.09.002 |
| [6] |
RUI Xiaoting, HE Bin, LU Yuqi, et al. Discrete time transfer matrix method for multibody system dynamics[J]. Multibody System Dynamics, 2005, 14(3): 317-344. |
| [7] |
ABBAS L K, BESTLE D, RUI Xiaoting. Transfer matrix method for the determination of the free vibration of two elastically coupled beams[J]. Applied Mechanics and Materials, 2013, 372: 301-304. DOI:10.4028/www.scientific.net/AMM.372 |
| [8] |
HENDY H, RUI Xiaoting, ZHOU Qinbo, et al. Transfer Matrix Method for Multibody Systems of TITO System Control Applications[J]. Applied Mechanics and Materials, 2014, 530-531: 1043-1048. DOI:10.4028/www.scientific.net/AMM.530-531 |
| [9] |
RONG Bao, RUI Xiaoting, WANG Guoping, et al. Discrete time transfer matrix method for dynamics of multibody system with real-time control[J]. Journal of Sound and Vibration, 2010, 329(6): 627-643. DOI:10.1016/j.jsv.2009.09.034 |
| [10] |
孔向东, 钟万勰. 非线性动力系统刚性方程精细时程积分法[J]. 大连理工大学学报, 2002, 42(6): 654-658. |
| [11] |
何斌, 陈树辉. 连续梁瞬态振动离散时间精细传递矩阵法[J]. 振动与冲击, 2008, 27(4): 4-7. |
| [12] |
BV0430-85. Germany defense warship construction code-impact security[S]. Koblenz Germany, 1987.
|
 2016, Vol. 48
2016, Vol. 48




