哈尔滨工业大学学报  2016, Vol. 48 Issue (2): 184-188  DOI: 10.11918/j.issn.0367-6234.2016.02.032
0

引用本文 

于天剑, 陈特放, 陈雅婷, 成庶. HMM在电机轴承上的故障诊断[J]. 哈尔滨工业大学学报, 2016, 48(2): 184-188. DOI: 10.11918/j.issn.0367-6234.2016.02.032.
YU Tianjian, CHEN Tefang, CHEN Yating, CHENG Shu. Fault diagnosis of bearing failure using HMMS[J]. Journal of Harbin Institute of Technology, 2016, 48(2): 184-188. DOI: 10.11918/j.issn.0367-6234.2016.02.032.

基金项目

国家自然科学基金（61273158）

作者简介

于天剑(1988-), 男, 博士研究生;
陈特放(1957-), 男, 博士生导师

通信作者

成庶, 6409020@qq.com

文章历史

收稿日期: 2014-12-22
Abstract              Full text              Figures/Tables              PDF
HMM在电机轴承上的故障诊断
于天剑, 陈特放, 陈雅婷, 成庶     
中南大学 交通运输学院, 410075 长沙
收稿日期: 2014-12-22
基金项目: 国家自然科学基金（61273158）
作者简介: 于天剑(1988-), 男, 博士研究生;
陈特放(1957-), 男, 博士生导师
通信作者: 成庶, 6409020@qq.com
摘要: 为了提高其机械系统故障诊断能力及其准确性，以历史的经验数据为基础对滚动轴承进行健康管理，提出一种新的基于多个隐马尔可夫模型与蚁群聚类算法（ACC）和神经网络相结合的方法来用于轴承故障的诊断与检测，该方法采用HMM与模式识别相结合的方法通过对轴承振动信号进行特征提取，在时频域内进行分析其老化的现象，分别将历史数据和新数据进行故障诊断和检测，并通过HMM和ANFIS来估计其剩余使用寿命和年限.实验结果表明：HMM与模式识别相结合的方法可以准确地对故障进行诊断及预测，通过对结果分析可以得到该方法降低了计算的复杂度，提高了诊断的精度，通过对不同故障诊断实例详细阐述了基于HMM故障诊断方法的有效性和可行性.
关键词: 故障诊断     隐马尔可夫模型     ACC     电机轴承     模式识别    
Fault diagnosis of bearing failure using HMMS
YU Tianjian, CHEN Tefang, CHEN Yating, CHENG Shu     
School of Traffic and Transportation Engineering, Central South University, 410075 Changsha, China
Abstract: In order to improve the fault diagnosis ability of the system and its accuracy, with previous experience in this article is based on data Rolling health management, this paper presents a novel based on multiple hidden Markov models and Kazuo artificial neural network algorithms and methods of combining ant colony to be used to diagnose and detect bearing faults, which uses HMM and pattern recognition method by combining the bearing vibration signal feature extraction, in the frequency domain analysis of the aging phenomenon, namely the historical data and the new data fault diagnosis and testing, while HMM and ANFIS fault prediction is to estimate the remaining useful life and the life. The experimental results show that the method of HMM and pattern recognition can be used to diagnose and predict the faults. The method can reduce the computational complexity and improve the accuracy of diagnosis, through the different fault diagnosis example elaborates on HMM-based fault diagnosis method effectiveness and feasibility.
Keywords: diagnosis     hidden Markov models     ACC     motor bearings     pattern recognition    

轴承在工业生产中一直扮演着很重要的角色，轴承的故障或者损坏会带来很严重的危害和重大的经济损失，准确地发现并探测出运行电机的故障有着很重要的意义[1]，新方法致力于开发故障诊断和预测的准确性，提高系统的安全性和可靠性，典型的轴承PHM系统包括特征提取、故障检测、故障诊断和故障预测[2-3]，特征提取方法有时域分析法、频域分析法和频谱分析法[4]，故障的诊断与检测方法有3个方面：基于模型式、数据驱动和基于经验基础的方法[5]，本文提出一种将数据模型和经验基础相结合的方法，数据驱动模型是用来检测退化状态的新方法，HMM是一种非平稳时间序列的统计建模方法[6]，广泛应用于众多领域当中(比如语音识别、电气设备状态监测、网络状态分析等方面)，而且着意于从概率角度刻画动态系统的内在状态与外在表现，既能反应对象的随机性，又能反应对象的潜在结构，适用于复杂动态系统的建模问题[7]，故本文提出了一种新的基于隐马尔可夫模型与模式识别及神经网络相结合来对电机轴承进行故障诊断及预测，可以快速、准确地探测轴承的异常行为，有利于轴承故障的早期发现及诊断[8].

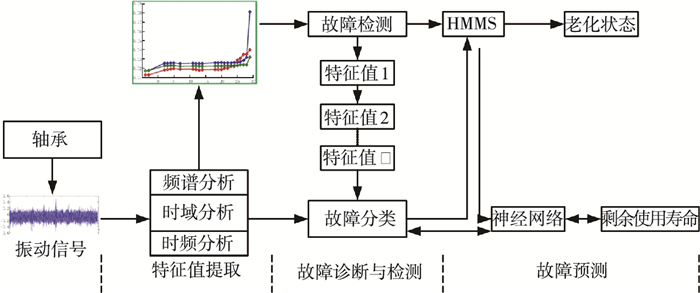
1 特征值提取与故障检测

系统结构框图如图 1所示.首先是特征值提取，从轴承中检测数据并用时域分析法进行处理以除去冗杂数据；故障诊断与检测，是将收集到的特征数据和历史数据在相同的条件下进行检测，并将这些数据通过ACC(蚁群聚类算法)进行检测；故障预测，是通过HMM方法和ANFIS方法进行故障预测.

图 1 轴承PHM系统

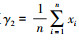
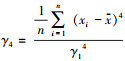
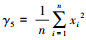
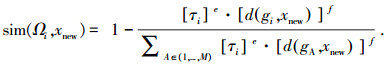
特征值的提取是在电机平稳运行下来提取各种指标来增加轴承PHM的有效性，特征值可以分为有效值、平均功率、峰值因子和峭度[9].峭度是一个很好判断轴承好坏的指标，一个轴承健康的时候的峭度为3，当轴承老化的时候其峭度会降低，而峰值因子在检测轴承故障的早期阶段最为有效，有效值和平均功率表示其真实的信号质量，在故障的定位方面会更为有效，当有效值和平均功率变高时会对应于一个轴承的整体恶化程度，平均加速度信号是标准的统计平均值，一个良好轴承的平均加速度值为零，当轴承出现恶化的时候其平均加速度会变大[10].各个特征值计算如下所示：均方根γ1=；均值；峰值因子γ3=；峭度；平均功率.其中的故障检测是在时域检测状态下的分类器，也就是故障识别方法，本文通过一个非线性的分类方法，即蚁群聚类算法来对故障进行检测，可以用一个故障分类的公式表示为

式中：d(gi, xnew)为一个测量数据，是其到中心数据的几何距离；(e, f)∈(0，1)；Ωi为分类数；d(gA, xnew)为新数据与历史数据的关系式；gi可以表示为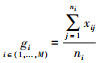，其中ni为数据Ωi的数量，是总数量，xij为Ωi的矢量化.

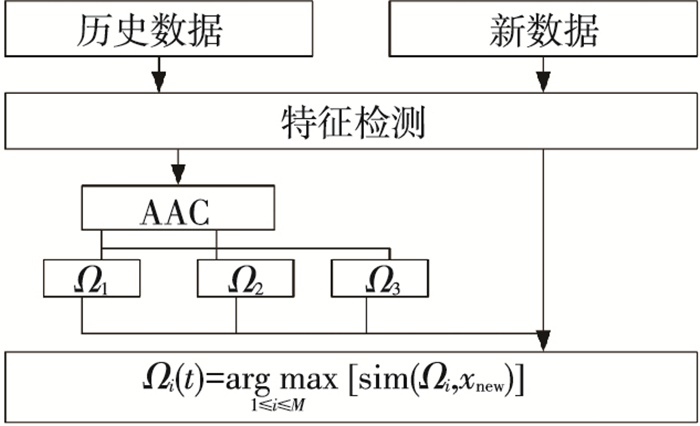
而其故障检测的步骤为先对历史数据和新数据进行特征检测，之后通过蚁群聚类算法对数据进行分类，然后再对其择优[11]，结构如图 2所示，其分类后数据状态值如图 3所示，通过对特征值进行三维特征空间标准化的仿真, 对历史数据进行分类.

图 2 故障的检测
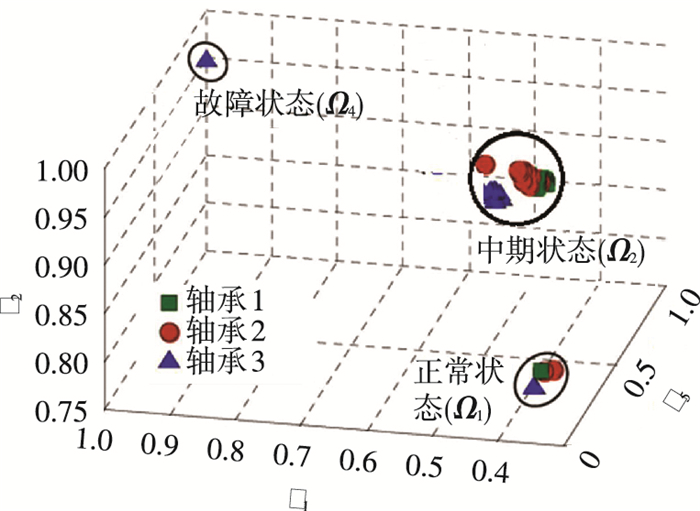
图 3 历史数据分类

从图 3可以看出，通过对历史数据进行分类，其中故障状态数据最少，中期状态的数据最多，也是符合轴承的实际工作情况，然后再利用这些选好的数据继续进行以下的故障预测.

2 故障的诊断及预测

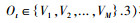
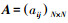
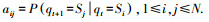
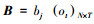
在本研究中应用了HMM方法来对轴承进行处理，HMM是一个双重随机过程，不仅状态之间的转移是随机的，而且每个状态的观测值也是随机的，但其中描述状态转移的马尔和夫过程是不能直接观测的，只能够根据观测过程进行推测，HMM是一个统计学的概率问题, 一个HMM可以由下列参数来描述[12]：1)模型的状态参数N，记N个状态为S1, S2, ..., SN，t时刻模型所处的状态为qt，显然qt∈{S1, S2, ..., SN}.2)每个状态可能观测值数目M，记M个观测值V1, V2, ..., VM，t时刻的观测值为Ot，则有状态转移矩阵A，, 1≤i, j≤N，其中4)观测矩阵B，，其中bj(ot)=P(ot|qt=Sj), 1≤j≤N, 0≤t≤T.5)初始状态矢量π，π=(π1, π2, ..., πN)，其中πi=P(q1=si), 1≤i≤N.

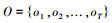
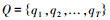
但在实际应用中，HMM必须解决下面的3个基本问题：1)HMM的输出概率计算问题.在给定模型参数λ=π, A, B的条件下，如何有效地计算特定的观测值序列的概率P(o|λ).2)HMM的最优状态序列问题.在给定模型参数λ=π, A, B和观测值序O={o1, o2, ..., oT}的条件下，如何选择一个对应的状态序列，能够最合理地解释该观测值序列.3)HMM的参数估计问题(又称模型训练问题)[13]，即如何调整模型参数λ=(π, A, B)，使得该模型产生观测值序列O={o1, o2, ..., oT}的概率P(o|λ)最大.

而Baum-Welch算法用于解决上述问题，参数估计的目标是调整模型参数λ，使产生训练数据O的概率最大，可以通过连续迭代和变换目标函数为

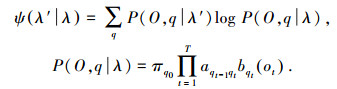
在该算法中不断更换λ和λ′直到得到合适的结果为止，通过此程序，获得更新HMM参数为A, B, π，即

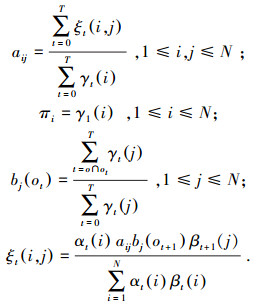
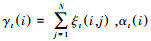
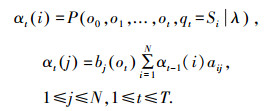
其中：分别为从初始时刻到t时刻模型的部分观测值序列O={o1, o2, ..., oT}和t时刻模型处于状态Si的联合概率，即

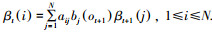
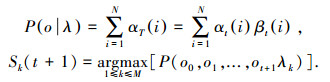
此时α0(j)=πjbj(o0), 1≤j≤N, 而βt(i)是从t+1时刻到最终时刻模型的部分观测值序列ot+1, ot+2, ..., oT的联合概率，βt(i)=P(ot+1, ot+2, ..., oT|qt=Si, λ)初始化, 递推.提取一系列的观测值和上面的前向后向算法所得到的最终联合概率为

从最后的公式中可以得出下一个时刻t+1时的状态，但此时的观测值Ot+1是不可用的，为此本文在此更换一个新的观测值Csj来代替Ot+1，同样bj(ot+1)是在0和1之间的值，也就是说通过一系列推导得到在t时刻Csj=bj(ot)，若Csj=1则为下一个可能发生的状态[14]，由此成为了一个新的过渡：

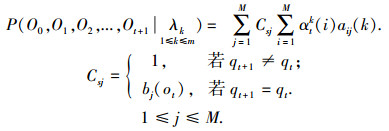
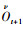
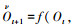
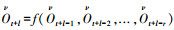
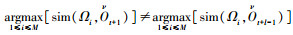
由于HMM方法可以准确地识别故障但很难预测未来的状态，然而HMM方法可以确定一个ANFIS模型，ANFIS是一个模糊推理的过程，应用在自适应神经网络中，被成功应用在故障预测当中，并且通过以前的研究表明，ANFIS是一个可靠的故障预测方法.对于轴承的历史数据可以分为训练集和验证集，训练集用于估计隶属度函数的参数，验证集用于验证系统的稳定性，在训练过程中权值和偏置值通过最小化误差来调整ANFIS的输出[15]，本文中为一个振动信号的统计值，通过加一个滑动的窗函数使得输出可以在t+1时刻预测出来.滑动窗函数的观测值为，所以Ot－1, ..., Ot－r)，其中r为滑动窗口的大小，重复该过程递归得到，并且满足.

3 实验结果

实际上在实验室轴承参数是很难准确地测量和实时检测的，由于在现场实验也有很大的难度，所以本文搭建一个实验平台，来进行模拟真正的运行工况，然而实验的过程并不能很快地反映轴承自然降解情况，通过人为地给其他轴承加径向负荷以及一些电工损伤或加快转速和运行时间来加快老化，这样更能方便地检测和分析结果.

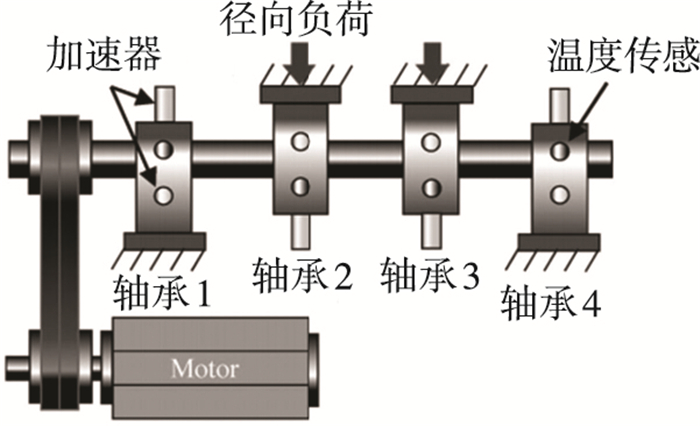
分别选取同样的4种轴承固定在同一个轴上，对于每个轴承给出不同的扭矩和负荷，其中转速为2 000 r/min，以恒定6 000 N的径向负荷放置在轴承上，如图 4所示，从实验中选取相对比较好跟踪的实验数据，如峭度、平均值、平均功率等.用来验证本文的诊断方法，用历史数据来检测未知状态下的退化状态，识别HMM模型参数.

图 4 轴承测试实验

其中图 5(a)为对平均功率的信号提取，从采集软件中本文注意到轴承(1, 2, 3, 4)在2 000 r/min和6 000 N的径向负荷下进行35 d的电工实验，可以看到第4根轴承有老化迹象，并且其平均功率有明显的增加.图 5(b)中为对其特征值峭度的提取，从图中可以看到经过28 d的测试实验第4根轴承开始老化，其峭度明显增加，在31 d后轴承3、4都开始老化并在第33 d达到最大值，可以看到这两个信号对故障的反映是十分重要的，再经过几天的操作以后数据没有明显大的改变.

图 5 特征值对比情况
4 故障预测

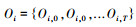
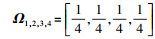
选取1 944组实验数据，其中1 458组数据为训练集(其他486组为1、2、3的观测值)，特征值γ1, γ2, γ6分别为轴承1、2、3的HMM和ANFIS的参数估计.对于HMM的故障预测，可以假定轴承在完好状态下为S1，在中期状态下为S2，要发生故障的状态为S3，故障状态下为S4.对于每一类观测值取观测长度为T=4来提取特征值，并在文献中已经验证了其可行性，用于观察序列估计的HMM参数可以归纳为，定义状态转移矩阵A和初始状态矢量π.

，可以得到HMM模型参数:

由状态转移矩阵和观测值(O1, O2, O3, O4)可以得到

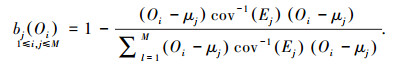
其中：Ej为Ωi的训练值，μj为中心变量.

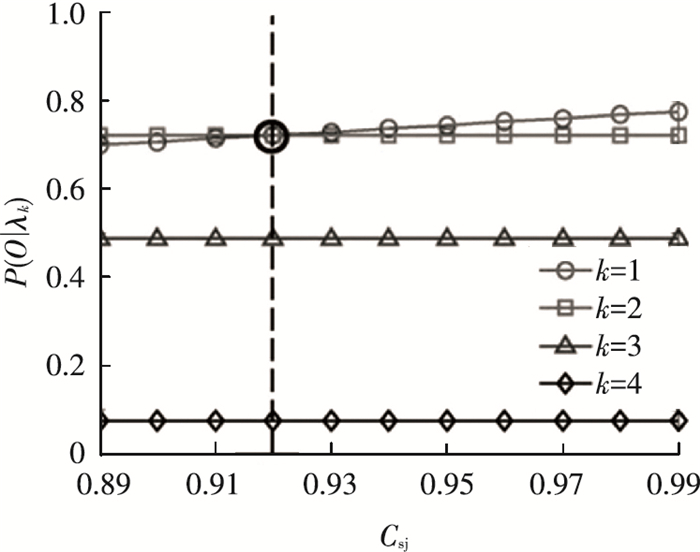
可以观测到其最大值P(OK|λK)相对于k=1, 2, 3, 4时，对ANFIS参数，选取3个参数(γ1, γ2, γ6)来预测未来的值，每个系统对应3个统计的特征值，轴承的历史数据集用来识别轴承1、2、3的故障情况，并且有3个隶属度函数用于输入ANFIS系统中，每个滑动窗函数的大小是固定的.可以从下面的仿真实验当中来验证本文方法的正确性.在图 6中可以看到轴承运行到5 553 min之前都是健康状态，而此时的系数值为b(Ot)=0.92，但是在之后的3 427 min之内都是在要发生故障的维持运行的状态，然而在9 176 min以后轴承则开始发生故障，可以在图 7中观测到4种观测值的概率情况，很清晰地看到在系数为0.92的情况下健康情况的概率为0.72，中期情况概率为0.5，故障情况下概率为0.09，因此图 7就是本文所预测的状态概率值，可以来验证实验方法的可行性.

图 6 轴承状态检测及预测
图 7 各种状态下的轴承概率值
5 结论

1) 针对历史数据是很难获得这一局限性，提出了一种新的应用在电机轴承的故障诊断及预测的方法.

2) 利用HMM方法与ANFIS方法相结合的情况来对故障问题进行建模、在频域内提取特征值、用ACC算法进行故障分类、最后用隐马尔可夫模型方法进行了故障预测，并且在实际试验当中验证了其方法的准确性与持久性，得到的结果表明所提出方法用于轴承检测、诊断、预警的可行性.

3) 提出了一个新的问题，即如何用HMM来定位具体轴承的故障位置，知道了故障如何快速找到故障位置，也是在今后的研究中有待解决的问题.

参考文献
[1]
FROSINI L, BASSI E. Stator current and motor efficiency as indicators for different types of bearing faults in induction motors[J]. IEEE Trans Ind Electron, 2010, 57(1): 244-251. DOI:10.1109/TIE.2009.2026770
[2]
IMMOVILLI F, COCCONCELLI M, BELLINI A, et al. Detection of generalized-roughness bearing fault by spectral-kurtosis energy of vibration or current signals[J]. IEEE Trans Ind Electron, 2009, 56(11): 4710-4717. DOI:10.1109/TIE.2009.2025288
[3]
ZHANG B, SCONYERS C, BYINGTON C, et al. A probabilistic fault detection approach:application to bearing fault detection[J]. IEEE Trans Ind Electron, 2011, 58(5): 2011-2018. DOI:10.1109/TIE.2010.2058072
[4]
IMMOVILLI F, BIANCHINI C, COCCONCELLI M, et al. Bearing fault model for induction motor with externally induced vibration[J]. IEEE Trans Ind Electron, 2013, 60(8): 3408-3418. DOI:10.1109/TIE.2012.2213566
[5]
YAZIDI A, HENAO H, CAPOLINO G A, et al. A webbased remote laboratory for monitoring and diagnosis of ac electrical machines[J]. IEEE Trans Ind Electron, 2011, 58(10): 4950-4959. DOI:10.1109/TIE.2011.2109331
[6]
BARUAH P, CHINNAM R B. HMMs for diagnostics and prognostics in machining processes[J]. Int J Prod Res, 2005, 43(6): 1275-1293. DOI:10.1080/00207540412331327727
[7]
RAMMOHAN R, TAHA M. Exploratory investigations for intelligent damage prognosis using hidden Markov models[C]//Proc 2nd IEEE Conf Systems Man and Cybernetics. Piscataway: IEEE Press, 2005: 1524-1529.
[8]
CHEN C, ZHANG B, VACHTSEVANOS G. Machine condition prediction based on adaptive neuro fuzzy and high-order particle filtering[J]. IEEE Trans Ind Electron, 2011, 58(9): 4353-4364. DOI:10.1109/TIE.2010.2098369
[9]
STRANGAS E, AVIYENTE S, NEELY J, et al. Improving the reliability of electrical drives through failure prognosis[C]//Proc 2nd IEEE Conf (SDEMPED). Piscataway: IEEE Press, 2011: 172-178.
[10]
MAHAMAD A K, SAON S, HIYAMA T. Predicting remaining useful life of rotating machinery based artificial neural network[J]. Comput Math Appl, 2010, 60(4): 1078-1087. DOI:10.1016/j.camwa.2010.03.065
[11]
BENKEDJOUH T, MEDJAHER K, ZERHOUNI N, et al. Fault prognostic of bearings by using support vector data description[C]//Proc 9th IEEE Conf Prognostics and Health Management. Piscataway: IEEE Press, 2012: 1-7.
[12]
于天剑, 陈雅婷, 陈特放. 基于HMM在电机故障诊断上的研究[J]. 铁道科学与工程, 2014, 11(4): 103-108.
[13]
ZAIDI S, AVIYENTE S, SALMAN M, et al. Prognosis of gear failures in DC starter motors using hidden Markov models[J]. IEEE Trans Ind Electron, 2011, 58(5): 1695-1706. DOI:10.1109/TIE.2010.2052540
[14]
CAMCI F, CHINNAM R. Hierarchical HMMs for autonomous diagnostics and prognostics[C]//Proc 9th IEEE Conf Neural Networks. Piscataway: IEEE Press, 2006: 2445-2452.
[15]
WANG T, YU J, SIEGEL D, et al. A similarity-based prognostics approach for remaining useful life estimation of engineered systems[C]//Proc 7th IEEE Conf Prognostics and Health Manage. Piscataway: IEEE Press, 2008: 1-6.