近年来快速发展的随机粗糙表面电磁散射理论和实验研究越来越引起人们的重视.许多理论和工程上的问题需要对粗糙面上的散射现象进行研究.有关粗糙面散射理论在雷达目标成像、材料物理、环境遥感等领域都有广泛的应用[1-2].关于粗糙面的电磁散射已有许多富有意义的研究成果,粗糙面散射研究中较为经典的近似方法是基尔霍夫近似.文献[3]提出了一种分析导体目标电磁散射特性的有效数值方法.文献[4]通过实验测定不同标准粗糙表面和典型目标表面密勒矩阵参数,得出具有高斯特性的不同粗糙表面的退偏振特性存在显著差异.文献[5]从实验角度测量样品表面的光散射轮廓,引入自仿射分形随机表面模型,成功提取了随机表面参量,并验证所得参量的正确性.文献[6]较完整地分析了具有分形特性的二维海平面的散射问题,其得出的结论对于静止和动态且不具有高斯分布特点的分形表面是适用的.文献[7]由二维随机粗糙面散射场方程出发,利用分形几何方法模拟随机粗糙面,研究了随机表面散射光场与随机粗糙面统计参量及其分形参量的关系.
以往的粗糙面散射研究中,通常采用特定的已知周期函数或随机函数作为粗糙表面的数学模型,但在自然界中粗糙面既非纯随机也非完全周期的[8].从统计意义上来讲,一般的二维随机粗糙面在一定的标度之间都存在着自相似性或自仿射性,具有分形特点.近年来有关一维分形粗糙面散射的研究较多,但到目前为止对更为接近于实际的,从分维角度研究二维分形粗糙面散射文献较少.本文通过采用修改的Weierstrass函数模拟二维分形粗糙面,利用基尔霍夫近似研究分形表面散射特性与分形参数之间的定量关系.
1 表面模型建立二维带限函数在表面模拟研究中应用广泛,Weierstrass模型反映了分形表面确定性的周期分量和随机分量组合,微观高度表达式[9]为
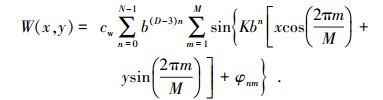
|
(1) |
其中:cw为常数,使得W(x, y)具有单位扰动幅度,大小取决于材料本身;b(b>1)为空间基频;D为分形维数, 2<D<3;K为基本波数;N、M均为谐波数,这两个参数控制着分形表面的各向异性程度;φnm为在[-π, π]上服从均匀分布的随机相位.
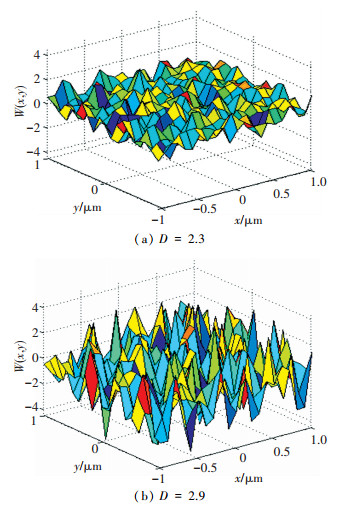
当N和M不太大时,在x方向和y方向上是各向异性的,它具有较大的偏导数和自仿射结构,即使在很小的尺寸下,该函数模型也具有相同的粗糙度,因此这种分形表面为多测度表面.由于自然界中实际的粗糙表面一般既不是纯随机的也不完全是纯周期的,且经常各向异性,因此式(1)是构建自然界分形粗糙面物理模型比较好的选择.当N=6, M=10, b=1.8不同分维下的二维分形表面模型如图 1所示.由图可见,当二维带限Weierstrass函数中主要参数b、N、M不变时,二维分形表面的粗糙程度主要由分维D决定.
|
图 1 不同分维下的分形表面模型 |
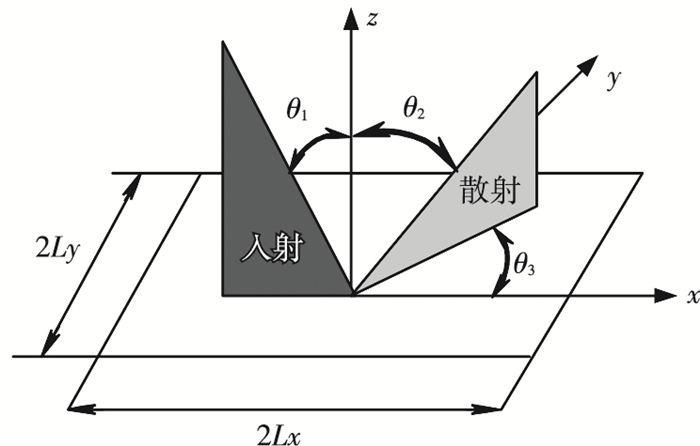
基尔霍夫近似理论又称为切平面近似,被广泛用来分析表面散射问题,它是将粗糙曲面用局部切平面代替,由菲涅尔反射定律获得切平面总场,从而近似计算远区散射场.本文利用基尔霍夫近似理论分析二维分形粗糙面散射特性,散射几何示意图如图 2所示.
|
图 2 二维带限分形粗糙面散射几何示意图 |
为了推导二维粗糙面的散射场,现作如下假设:散射远场作为观测点,入射波为单一平面波,平面上任意一点具有有限坡度,反射系数为常数,粗糙面单向尺寸远大于入射波长.此时散射场矢量ψsc(r)表达式可通过入射角θ1、散射天顶角θ2和散射方位角θ3等表示为[10-11]
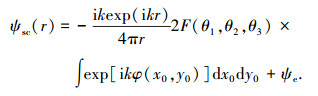
|
(2) |
其中:
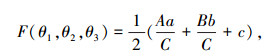
|
(3) |
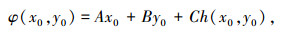
|
(4) |
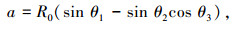
|
(5) |
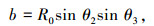
|
(6) |
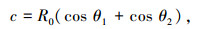
|
(7) |
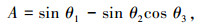
|
(8) |
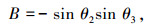
|
(9) |
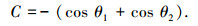
|
(10) |
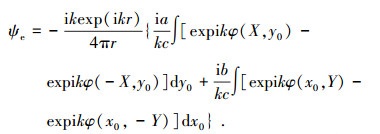
|
(11) |
式中:Ψe为边缘效应;(x0, y0)为二维分形表面上任意一点,且满足-Lx≤x0≤Lx, -Ly≤y0≤Ly;k为入射波波数,且有k=2π/λ;λ为入射波波长,R0为菲涅尔反射系数,在采用HH极化时,菲涅尔反射系数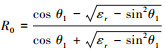
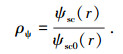
|
(12) |
式中ψsc0(r)指近光滑分形表面镜像方向的散射场强,
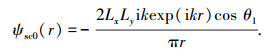
|
(13) |
在镜像方向上,有θ1=θ2,θ3=0,A=0,B=0以及a=0,b=0,由式(5)~(10)可得,二维分形表面散射场的平均散射系数ρψ由式(12)简化为
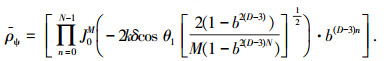
|
令
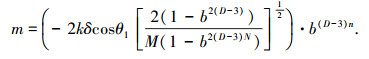
|
当m<1时,对ρψ取二阶近似,可以得到
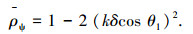
|
(14) |
式(14)表明二维分形粗糙面的平均散射系数ρψ主要与入射波波数k,粗糙面的均方根高度δ以及入射角θ1有关.由此得知,具有分形特性的表面与高斯随机表面镜向方向有相似的散射特性.
2.2 散射场的平均强度系数散射场的平均强度定义为
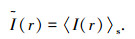
|
(15) |
与平均散射系数推导过程类似,可得散射场的平均强度系数ρI为
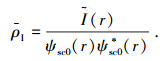
|
(16) |
采用和本小节开头一样的假设,分形表面散射场平均强度系数的离散表达式为
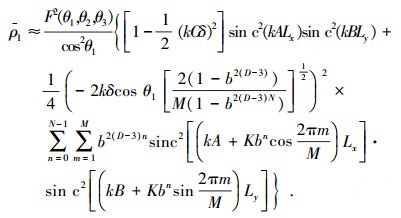
|
(17) |
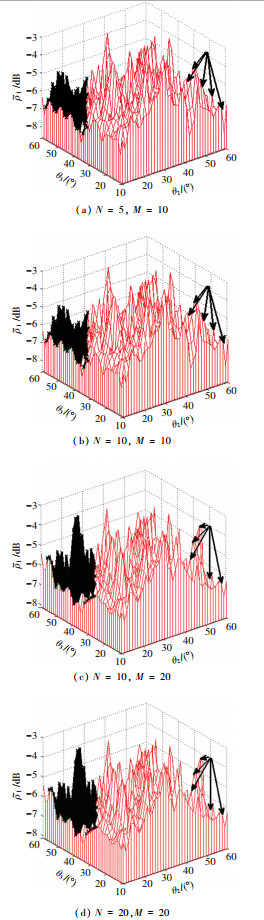
图 3(a)~3(d)描述了由式(17)给出的平均强度数值结果,其中b=1.8, D=2.5, δ=0.05λ, θ1=30°, K=0.5λ-1, Lx=30λ. 图 3(a)和3(b)表示的是正弦光栅和各向同性表面结合的各向异性表面的平均强度系数;图 3(c)和3(d)表示的仅仅是一种各向同性表面的平均强度系数.由于这4个表面有相同的均方根高度,相同的入射角和波长,因此,在镜像方向上这两种散射强度具有基本相同的特定值.
|
图 3 二维分形表面平均强度数值结果 |
图 3(a)和3(b)、图 3(c)和3(d)表明,N的变化对平均强度系数影响不大,各峰值的分布位置基本不变,只有微小的峰值变化,且当M较小时,散射主要集中在特定平面和特定方向上及其附近的区域;对比图 3(a)和图 3(d)可得,随着M的增大,在镜向反射点以外会出现越来越多的旁瓣分量,且分量的幅值是增大的.由图 3的4个分图可以看出,随着分形表面各向同性分量的增加,更多的散射强度分量出现在非镜像方向和沿着θ2的垂直平面方向上,镜像方向上的散射对于探求分形参数对散射场不同影响有重要意义[14].
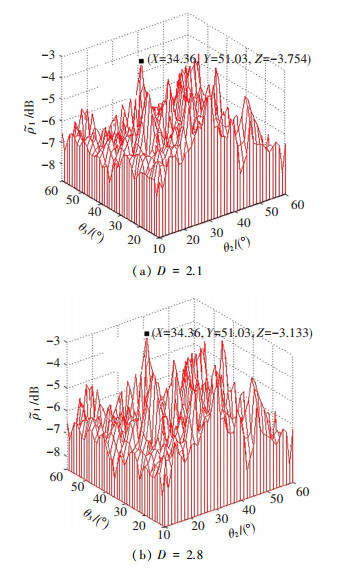
当λ=2 μm时平均强度系数ρI随着D变化的情况如图 4所示,其中δ=0.05λ, b=1.8, θ1=30°, K=0.5λ-1, Lx=Ly=30λ.
|
图 4 平均强度系数ρI随着分维D的变化 |
由图 4可见,在其他参考变量不变的情况下,分维D对散射强度系数ρI的影响主要体现在各峰值的大小、数目及位置.随着分维D的增大,在镜向反射点以外会出现越来越多的旁瓣分量,且峰值是增大的.
由散射场的统计参量定义,可推得表征与平均散射场均方根高度相关的强度系数σI为
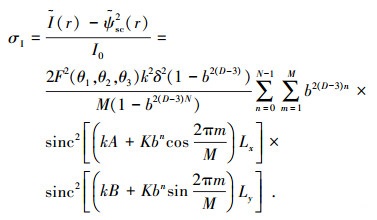
|
(18) |
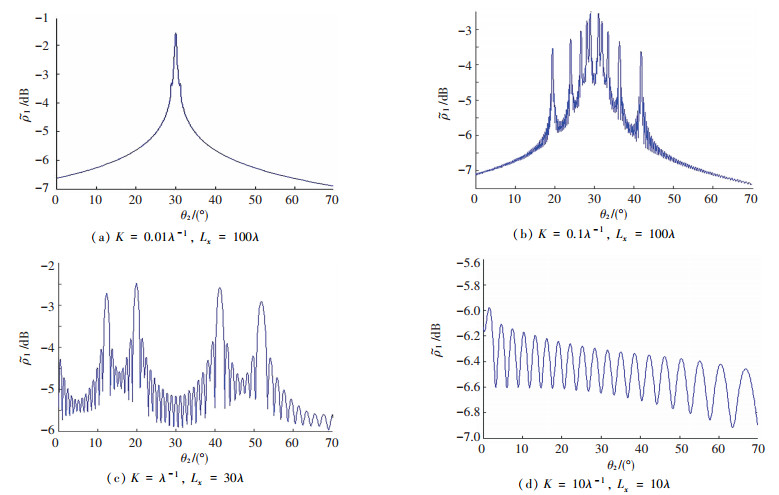
显然σI代表的是强度相关的非相干分量平均值,它主要用来分析除镜像以外的散射场,分形参量对其有显著的影响.采用式(18)的优点在于只需考虑散射场和散射强度的平均效应,而无需考虑较难获得的散射波前相位项的影响.根据式(18)可将参数选择为b=1.8, N=5, M=10, D=2.5, δ=0.05λ, 然后选择4种不同的散射形式(K=0.01λ-1, 0.1λ-1, λ-1和10λ-1)对应如图 5所示.
|
图 5 二维分形表面不同散射强度系数 |
对于K≤0.01λ-1, 如图 5(a)所示,散射场的高频分量集中在镜像方向,对于这种表面而言,非镜像方向散射强度会迅速下降,与近光滑表面散射特性基本相同,入射波长远小于若干个空间周期,计算结果趋近于几何光学近似.当K≥10λ-1对应图 5(d),空间周期远小于入射波长,此时散射不满足基尔霍夫近似的条件,散射场的均方根高度δ处处很小,该方法计算结果不可信,这种散射特性与完全均匀表面接近,此时入射波波长可以看成“小棍”用来测量粗糙表面.对于0.01λ-1<K<10λ-1更多的高频分量出现在非镜像方向,而高频分量的衰减可用来分析表面参数对散射场的影响.即可以对于一个已知的表面,在研究其散射特性时,应通过仔细选择适当的尺寸,明确K值的取值范围,进而选择合适的入射波长,就可以获得满意的散射模型.
4 结论1) 在采用二维带限Weierstrass分形函数模拟二维分形粗糙面的基础上,利用基尔霍夫近似研究了该粗糙面的平均散射系数和散射强度系数.结果表明,对于微观高度表达式中的每一个参量都影响着二维分形表面的散射特性,谐波数N、M和空间波数K都决定着散射场中旁瓣分量的位置和大小,应当注意K的选取与波长有关.
2) 谐波数N和M也不能太小,否则粗糙表面将会变得很光滑,分形特性无法显现.分析结果可用于粗糙面遥感和测量等研究,同时也可用于粗糙表面的分类以及根据所测得的不同形式散射场重构粗糙表面等逆问题.
| [1] |
MACELLONI G, PAMPALONI P. Experimental validation of surface scattering and emission models[J]. IEEE Trans on GARS, 2000, 38(1): 459-469. |
| [2] |
田炜. 随机粗糙面光散射特性研究[D]. 西安: 西安电子科技大学, 2009. http://cdmd.cnki.com.cn/Article/CDMD-10701-2009195547.htm
|
| [3] |
王仲根, 孙玉发, 王国华, 等. 应用改进的快速偶极子法和特征基函数法分析导体目标电磁散射特性[J]. 电子与信息学报, 2013, 35(9): 2273-2277. |
| [4] |
江舒, 来建成, 王春勇, 等. 典型粗糙表面的退偏振特性实验研究[J]. 南京理工大学学报(自然科学版), 2011, 35(3): 294-297. |
| [5] |
孔德见, 何乃霞, 程传福, 等. 各向异性随机表面参量的光散射测量[J]. 山东师范大学学报(自然科学版), 2010, 25(1): 64-66. |
| [6] |
BERIZZI F, DALLE-MESE E. Scattering coefficient evaluation fr om a two-dimensional sea fractal surface[J]. IEEE Trans on Antennas Propagate, 2011, 50(4): 426-434. |
| [7] |
张连波, 郭立新, 苟雪银, 等. 三层粗糙面电磁散射的矩量法研究[J]. 西安电子科技大学学报, 2013, 40(6): 147-154. |
| [8] |
ULABY F T, MOORE R K, FUNG A K. Microwave remote sensing(active and passive) Ⅱ[M]. New York: Addison Wesley, 1982.
|
| [9] |
OGILVY J A. Theory of wave scattering from random rough surface[M]. Bristol: Adam Hilger, 1991.
|
| [10] |
SULTAN-SALEM A K, TYLER G L. Validity of the Kirchhoff approximation for electromagnetic wave scattering from fractal surfaces[J]. IEEE Trans Geoscience and Remote Sensing, 2004, 42(9): 1860-1870. DOI:10.1109/TGRS.2004.832655 |
| [11] |
LIN N, LEE H P, LIM S P. Wave scattering from fractal surfaces[J]. Journal of Modern Optics, 1995, 42(1): 225-241. DOI:10.1080/09500349514550181 |
| [12] |
JAGGARD D L, SUN X G. Scattering from fractally corrugated surfaces[J]. Journal of the Optical Society of America A:Optics, Image Science and Vision, 1990, 7(6): 1131-1139. DOI:10.1364/JOSAA.7.001131 |
| [13] |
LEUNG T, JIN A K, KUNG H D. Scattering of electromagnetic waves (numerical simulations)[M]. New York: Wiley-Interscience, 2001.
|
| [14] |
GIUSEPPE R, PABLO B S, ANTONIO I. Measurement of the electromagnetic field backscattered by a fractal surface for the verification of electromagnetic scattering models[J]. IEEE Trans on GRS, 2010, 48(4): 1777-1779. |
 2016, Vol. 48
2016, Vol. 48


