2. 安徽大学 工业节电与电能质量控制省级协同创新中心, 230039 合肥
2. Collaborative Innovation Center of Industrial Energy Saving and Power Quality Control, Anhui University, 230039 Hefei, China
随着工业智能化的迅速发展,具有多个自由度运动的执行机构的应用越来越广泛,然而传统的多自由度电机往往是由多个单自由度电机协调控制,这种机构体积庞大,控制难度大,精度低.本文提出的新型“蝶形”转子偏转式三自由度运动电机不仅能够实现三自由度运动,还具有体积小、重量轻、力能指标高、控制简单等优点,因此在机器人、机械手臂、电动陀螺、机床加工以及全景摄像云台等设备中都有着广泛的应用前景[1-3].
从上世纪50年代起,各国学者纷纷开始对球形电机展开研究.英国Sheffield大学设计出了二自由度永磁球形电机,利用霍尔传感器来检测转子位置,基于洛伦兹力法建立电机转矩模型[4-5]. 1999年,美国约翰霍普金斯大学设计了一种永磁球形步进电动机,并利用纯几何方法与函数分析方法对电机换相问题进行了分析[6-7].近年来,新加坡南洋理工大学Yan L等研制了可实现自转、倾斜和俯仰的三自由度永磁球形直流电动机,国内的研究人员也在致力于新结构多自由度电机的研究和创新[8-12].本文提出的新型永磁“蝶形”转子偏转式三自由度电机可在以绕Z轴自转为主的情况下实现绕X轴和Y轴适当的偏转.本文首先对该电机结构参数和工作原理进行介绍,采用解析法对电机气隙磁场和转矩进行建模和分析计算.在此基础上,对气隙磁场空间谐波含量对基波磁通密度和转矩幅值的影响进行分析.为了验证解析法建模的正确性,本文采用有限元分析方法分别对磁场和转矩进行了分析,建立了三维电机结构模型.最后通过对两种方法的对比,验证了解析法模型建立的正确性,为进一步电机通电策略和悬浮的研究提供了理论依据.
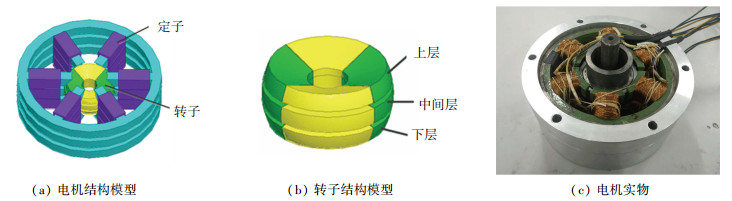
1 新型永磁转子偏转式三自由度电机结构 1.1 电机结构本文采用定转子磁极为“4-6”配合的永磁转子偏转式三自由度电机为分析对象,电机模型结构及实物如图 1所示,其中电机转子采用钕铁硼材料,形状近似“蝶形”,分为3层,每两层之间的夹角为20°.为了更好对电机进行控制,定子线圈也采用3层结构,每层6个共18个的排列方式.通过对不同定子线圈通电,可以实现在自转为主的情况下进行适当偏转,完成三自由度运动[13].
|
图 1 电机结构及实物图 |
永磁转子偏转式三自由度电机的工作原理是以永磁体产生的磁场和定子线圈通电后产生的磁场相互作用为基础,根据同性磁极产生的作用力相互排斥,异性磁极产生的作用力相互吸引的原理来驱使电机完成三自由度的运动.以绕X轴偏转为例,如图 2所示,当给1-2, 3-5号定子线圈施加直流电,使其产生N极;给2-2, 3-2, 1-5, 2-5号线圈施加直流电,使其产生S极,合成的电磁力将会驱动电机转子沿X轴偏转运动.同理,通过对不同位置的定子线圈及通电个数进行控制,可以使得电机完成三自由度的运动.

|
图 2 电机绕X轴运动工作原理 |
由于该电机转子采用3层蝶形转子结构,需要在球坐标系下求解三维气隙磁场.永磁转子偏转式三自由度电机气隙磁场由定子线圈和转子磁极共同产生,但由于定子线圈通电产生的磁场较转子磁极产生的小很多,因此转子磁极产生的外部磁场是气隙磁场的主要部分.以下主要对转子磁极外部气隙磁场进行分析[14-16].
由于本电机结构的转子是由3层“圆鼓形”转子叠加组合成的“蝶形”新结构,因此在计算气隙磁场时采用的分层计算, 然后再相叠加的方法.当永磁材料内部磁场移动时,永磁体的剩余磁化强度相应发生变化,能够在其周围产生新的磁场[17-18].因此在球坐标系,上层永磁体剩余磁化强度为

|
(1) |
式中:

|
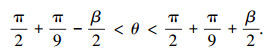
|
中间层永磁体剩余磁化强度为
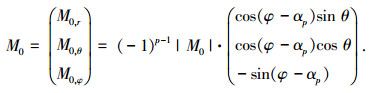
|
(2) |
式中:
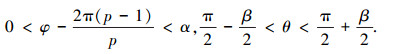
|
下层永磁体剩余此磁化强度为
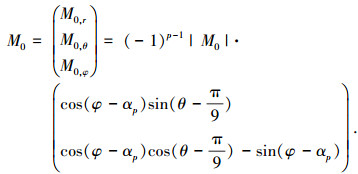
|
(3) |
式中:

|
球坐标系下拉普拉斯方程的表达式为
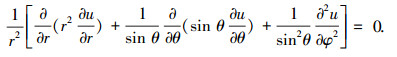
|
(4) |
由球谐函数理论可以求得,在球坐标下三维标量磁位解析方程的通解可以表示为
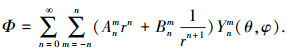
|
(5) |
式中:Anm、Bnm为未知系数,通过边界条件的限定可以得到具体数值,并推导出各层永磁体产生的磁通密度分别为
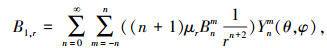
|
(6) |
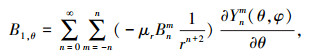
|
(7) |
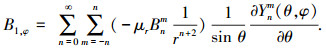
|
(8) |
通过分层计算出上、中、下3层转子磁极分别产生的气隙磁场,然后将3层磁极产生的气隙磁场进行叠加,既可以得到该蝶形转子电机产生的气隙磁场.
2.2 解析法磁场谐波分析永磁“蝶形”转子偏转式三自由度电机的气隙磁场沿θ和φ方向具有不同阶次的谐波含量,这些谐波含量的阶次与幅值由剩余磁化强度M0r的球谐函数系数Cn, m决定,其中m决定了沿φ方向的谐波分量阶次,而n决定了沿θ方向的谐波分量阶次.由剩余磁化强度Mrr(θ, φ)展开的连带勒让徳函数的二重广义傅立叶级数形式为
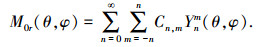
|
(9) |
其中Cn, m=|Mr|cmn(am±bmi).
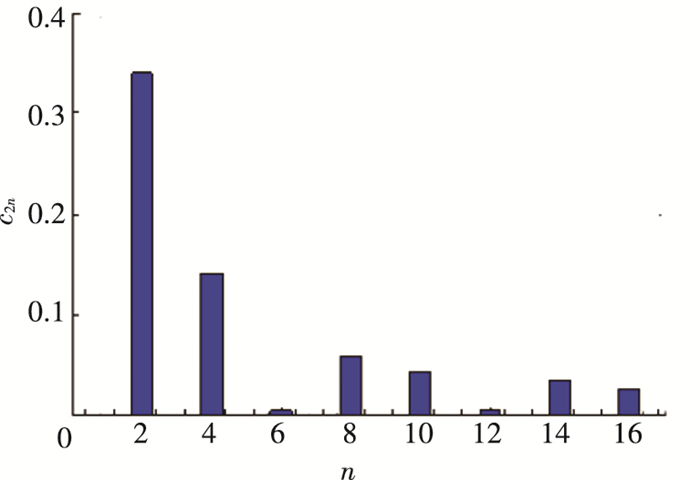
设Q=|am±bmi|,图 3、4分别给出了Q=|am±bmi|和c2n随m、n的变化.由图 3可看出,当m=2, 6, 10, 14, 22, 26, 30时,Q≠0.对于极对数p=2的磁体结构,磁场沿φ方向的谐波分量次数为v=m/2, m=2为磁场沿φ方向的基波含量,且在各次谐波中,基波含量最大.由图 4可以看出,m=2时,磁场沿θ方向谐波含量相当丰富,磁场沿θ方向的谐波分量次数为ω=n/2, 同样n=2为磁场沿θ的基波含量.

|
图 3 Q随m的变化 |
|
图 4 c2n随n的变化 |
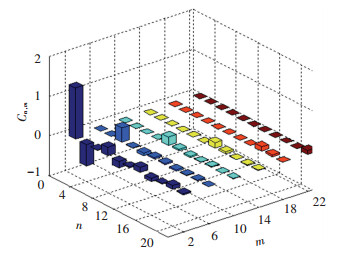
由于谐波含量的幅值与阶次是由转子磁极的剩余磁化强度系数Cn, m决定,图 5给出了球谐函数Cn, m的分布.由图可看出,当m=2, n=2, 4, 6, 8, …时,Cn, m≠0.随着阶次n的增加,幅值逐渐减小.因此,当球谐函数阶数为m=2, n=2时求解的结果为气隙磁场的基波分量,且基波分量幅值最大.
|
图 5 球谐函数系数Cn, m |
由以上分析可知气隙磁场中基波含量最高,且只有气隙磁通密度的径向分量能够产生电磁转矩,因此将气隙磁密径向基波分量进行提取. 图 6为气隙磁密基波分量B1r沿θ和φ方向的变化.从图 6可知,气隙磁通密度基波分量沿φ方向按余弦曲线分布,在两极交界处幅值达到最大,沿赤道一周具有两个正峰值点和两个负峰值点,这与蝶形转子4极磁体结构相一致;沿θ方向出现与转子3层结构相符的3层波形,且中间层转子磁极产生的气隙磁通密幅值大于上、下两层的气隙磁通密度,即在θ=90°时,磁密幅值最大.

|
图 6 径向气隙磁密基波分量空间分布 |
在求解转子偏转式三自由度电机转矩时,为了使得球坐标系下的计算更简便,将线圈用圆锥形来近似代替进行计算.运用洛伦兹力法可求得的每个线圈dl上产生的电磁力为

|
(10) |
由于该电机气隙磁场中只有沿r方向产生的电磁力才能产生驱动电机旋转的力,因此本文通过求取气隙磁通密度径向分量来求解电机转矩,即
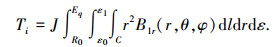
|
(11) |
“蝶形”转子偏转式三自由度电机可以实现绕Z轴自转和沿X,Y轴偏转,因此将转矩求解分为自转转矩求解和偏转转矩求解,可以表示为

|
(12) |

|
(13) |
图 7、8分别给出了电机自转转矩和偏转转矩的三维空间分布图.由图 7可知,自转转矩在一个周期内具有4个极值,变化趋势与气隙磁通密度径向分量相似.当φ=k·90°(k=0, 1, 2, 3)时出现极值,在φ=k·45°(k=1, 3, 5, 7)时为0.自转转矩沿θ方向,在θ=90°时达到最大值.由图 8可以看出,偏转转矩沿φ方向按正弦曲线变化,其周期为自转转矩的两倍,在φ=k·45°(k=1, 3, 5, 7)时偏转转矩取得最值,在φ=k·90°(k=0, 1, 2, 3)时为0.偏转转矩沿θ方向,在θ=90°时为0.由于转子采用3层结构,自转转矩和偏转转矩会出现与3层结构相符的变化趋势.

|
图 7 自转转矩分布 |

|
图 8 偏转转矩分布 |
有限元法是以变分原理和离散化近似差值为基础的一种数值计算方法.本文利用有限元软件对该新型三自由度电机结构进行建模分析[19-21].在求解三维静磁场的过程中, 磁感应强度B(x, y, z)是在x, y, z3个方向的矢量函数.由于只有气隙磁通密度的径向分量能够产生电磁转矩,因此基于有限元分析原理,图 9给出了气隙磁通密度径向分布,由图可知,由于有限元仿真得到的气隙磁通密度径向分量包含各次谐波,因此在空间内近似平顶波,出现两个波峰、两个波谷,与电机四极转子结构相符.

|
图 9 有限元法径向气隙磁密空间分布 |
图 10、11分别给出了有限元分析的自转和偏转转矩分布图.由图 10可以看出,通过有限元仿真出的自转转矩沿φ方向,在一个周期之内具有两个波峰和两个波谷,这与电机转子四极结构相符.沿θ方向,在90°时达到最大值0.231 31. 图 11中,与自转转矩一样,偏转转矩沿φ方向会出现4次波峰和四次波谷.沿θ方向在90°时,偏转转矩为0.在40°~140°时从中间向两侧有增大的现象,但在两层转子之间会相对减小,这主要是由于电机转子产生的3层磁场所致即两层转子之间缝隙处磁场明显减小.通过对自转转矩和偏转转矩进行分析,为电机的通电策略提供了一定的理论依据.

|
图 10 有限元法自转转矩空间分布 |

|
图 11 有限元法偏转转矩空间分布 |
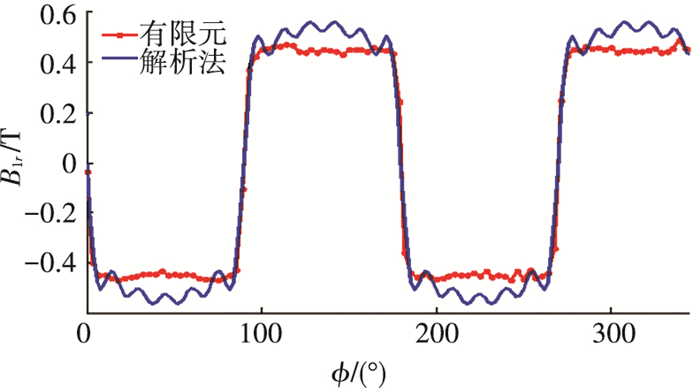
通过将解析法和有限元法进行对比,说明了解析法建模的正确性,其中为了提高可比性并且使比较结果更加准确,解析法在计算过程中加入了3、5、7、9、11次谐波,气隙磁场的对比结果如图 12所示.从图可知,解析法和有限元法变化趋势一致,一个周期内出现了两个波峰和两个波谷.两者幅值略有差别,其中加入谐波后的解析法最大值为0.511 25 T,有限元法最大值为0.487 64 T,解析法幅值略大于有限元法幅值,这主要是由于有限元在仿真计算时考虑的谐波次数比解析法多,而增加的谐波含量对基波含量具有削弱的作用.
|
图 12 B1r沿φ方向的对比 |
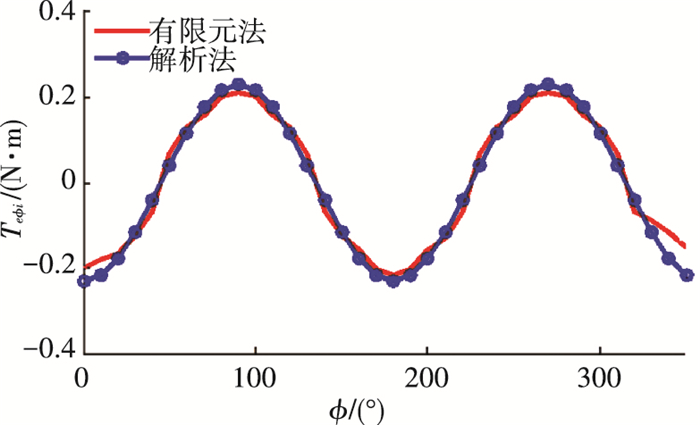
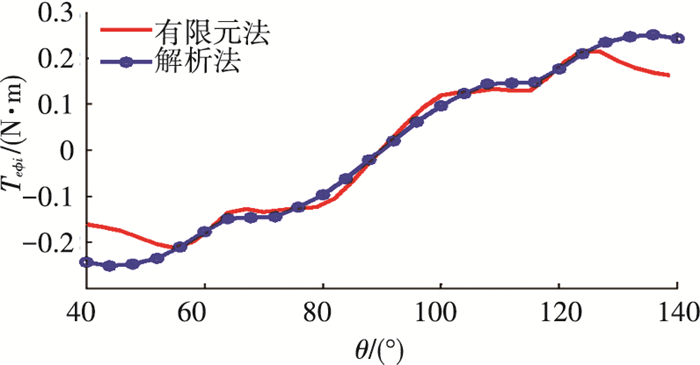
图 13和图 14对电机自转转矩沿φ方向和偏转转矩沿θ方向的解析模型和有限元模型进行了对比分析.由图 13可知,由解析法和有限元法获得的蝶形转子偏转式三自由度电机自转转矩的分布基本一致,两种方法的主要差别在于:有限元法的幅值略小于解析法,有限元法最大值为0.231 31 N·m,解析法最大值为0.241 67 N·m.从图 14可以看出,偏转转矩在θ=90°时幅值为0,向两侧逐渐增大,但方向相反,在两层交界缝隙处偏转转矩有所减小,这与转子3层结构和其产生的磁场相一致.两种方法所得结果变化趋势一致,解析法模型最大值为0.243 83 N·m,有限元法最大值为0.228 94 N·m,有限元法计算幅值大于解析法,且在转子两端部具有减小的特点,这主要是由于转子在不同的纬度线上的漏磁不同,距离赤道越远漏磁越大,因而当转子偏转到40°附近时,转矩幅值明显减小,当偏转角度再增大时,电机转矩将逐渐减小到0.
|
图 13 自转转矩对比 |
|
图 14 偏转转矩对比 |
表 1对解析法和有限元法对比的结果进行了总结,将气隙磁场φ方向分量Bφ和θ方向分量Bθ,自转转矩Tφ和偏转转矩Tθ的值进行了计算对比.由表 1可知,解析法和有限元法磁场和转矩计算:气隙磁场φ方向误差为4.6%, θ方向误差为6.7%,自转转矩φ误差为4.28%, 偏转转矩误差为6.11%,误差均小于6.7%.
| 表 1 解析法和有限元法数据比较 |
通过以上将磁场模型和转矩模型分别采用解析法和有限元法进行对比,得出两种方法所得磁场和转矩变化趋势一致,进而验证了解析模型的正确性.在对比分析过程中发现,解析法计算结果略大于有限元法,这主要是由于解析法建模过程中忽略了高次谐波,端部效应以及漏磁的影响,并简化了电机边界条件.与解析法相比,有限元法更接近真实值.但解析法表达式为显性,更适合于对电机性参数进行分析.
5 结论1) 分别采用解析法和有限元分别对新蝶形转子偏转式三自由度电机的磁场和转矩进行了建模和分析.通过磁场分析可得知该电机气隙处磁通密度沿φ方向的谐波含量主要3、5、7、9等奇数次,而θ方向谐波含量相当丰富.
2) 有限元法在仿真计算过程中不可避免地将所有谐波含量、漏磁和端部效应等影响加以考虑,因此气隙磁通密度在空间的分布近似平顶波,磁场和转矩的幅值略小于解析法.转矩的空间分布和磁场相似,只是出现幅值的位置不同.
3) 通过将解析法和有限元法的对比,结果表明有限元法仿真出的气隙处磁场、转矩值与解析法计算的结果相吻合,进而验证了解析法磁场和转矩建模的正确性,并为电机通电策略和控制的研究奠定了基础.
| [1] |
YAN L, CHEN I M, LIM C K. Modeling and iron-effect analysis on magnetic field and torque output of electromagnetic spherical actuators with iron stator[J]. IEEE/ASME Transactions on Mechatronics, 2012, 17(6): 1080-1087. DOI:10.1109/TMECH.2011.2159238 |
| [2] |
PARK H J, LEE H J, CHO S Y, et al. A performance study on a permanent magnet spherical motor[J]. IEEE Transactions on Magnetics, 2013, 49(5): 2307-2310. DOI:10.1109/TMAG.2013.2238616 |
| [3] |
李争, 王群京. 永磁多维球形电动机的研究与发展现状[J]. 微特电机, 2006, 33(10): 7-11. DOI:10.3969/j.issn.1004-7018.2006.10.003 |
| [4] |
李争, 王咏涛, 葛荣亮, 等. 永磁球形多自由度电机研究进展综述[J]. 微电机, 2011, 44(9): 66-70. |
| [5] |
王群京, 李争, 夏鲲, 等. 新型永磁球形步进电动机结构参数及转矩特性的计算与分析[J]. 中国电机工程学报, 2006, 26(10): 158-165. DOI:10.3321/j.issn:0258-8013.2006.10.029 |
| [6] |
李景灿, 廖勇. 考虑饱和及转子磁场谐波的永磁同步电机模型[J]. 中国电机工程学报, 2011, 31(3): 60-66. |
| [7] |
LI Bin, LI Hongfeng. Magnetic field analysis of 3-DOF permanent magnetic spherical motor using magnetic equivalent circuit method[J]. IEEE Transactions on Magnetics, 2011, 47(8): 2127-2133. DOI:10.1109/TMAG.2011.2123102 |
| [8] |
LI Zheng. Analysis and control of novel deflection-type PM multi-DOF actuator[J]. Journal of Harbin Institute of Technology, 2013, 20(2): 99-105. |
| [9] |
LEE H J, PARK H J, RYU G H. Performance improvement of operating three-degree-of-freedom spherical permanent-magnet motor[J]. IEEE Transactions on Magnetics, 2012, 48(11): 4654-4657. DOI:10.1109/TMAG.2012.2200470 |
| [10] |
LEE K M, SON H. Distributed multipole models for design and control of PM actuators and sensors[J]. IEEE/ASME Transactions on Mechatronics, 2008, 12(2): 228-238. |
| [11] |
LI Zheng, WANG Yongtao. Finite element analysis and structural optimization of a permanent magnet spherical actuator[J]. Electronics and Electrical Engineering, 2011, 114(8): 67-72. |
| [12] |
STEIN D, CHIRIKJIAN G S. Experiments in the commutation and motion planning of a spherical stepper motor[C]//Proceedings of ASME 2000 Design Engineering Technical Conferences and Computers and Information in Engineering Conference. Baltimore: ASME, 2000: 1-7.
|
| [13] |
李争. 永磁转子偏转式三自由度运动电机: 201110092529. 7[P]. 2014-07-23.
|
| [14] |
秦伟, 范瑜, 李硕, 等. 电磁电动式磁悬浮装置的磁场分析和力特性研究[J]. 电机与控制学报, 2012, 16(1): 67-71. |
| [15] |
ONER Y, ALTINTAS A. Computer aided design and 3D magneto static analysis of a permanent magnet spherical motor[J]. Journal of Applied Science, 2007, 7(22): 3400-3409. DOI:10.3923/jas.2007.3400.3409 |
| [16] |
DEHEZ B, GALARY G, GRENIER D, et al. Development of a spherical induction motor with two degrees of freedom[J]. IEEE Transactions on Magnetics, 2006, 42(8): 2077-2089. DOI:10.1109/TMAG.2006.876473 |
| [17] |
吴立建. 稀土永磁球形电动机的研究[D]. 合肥: 合肥工业大学, 2004. http://cdmd.cnki.com.cn/Article/CDMD-10359-2004084374.htm
|
| [18] |
王群京, 钱喆, 李争, 等. 基于机器视觉的永磁球形步进电动机转子位置检测方法[J]. 中国电机工程学报, 2008, 36(2): 73-78. |
| [19] |
STEPHEN L S, KIM D G. Force and torque characteristics for a slotless lorentz self-bearing servomotor[J]. IEEE Transactions on Magnetics, 2002, 38(4): 1764-1773. DOI:10.1109/TMAG.2002.1017769 |
| [20] |
LI Zheng. Robust control of PM spherical stepper motor based on neural networks[J]. IEEE Transactions on Industrial Electronics, 2009, 56(8): 2945-2954. DOI:10.1109/TIE.2009.2023639 |
| [21] |
LI Zheng, SUN Huiqin, WU Xueli, et al. Modeling and levitation control of a novel M-DOF actuator based on neural network[J]. International Journal of Applied Electromagnetics and Mechanics, 2012, 38(4): 217-230. |
 2016, Vol. 48
2016, Vol. 48



