2. 中国民航机场建设集团公司, 710075 西安
2. China Civil Airport Construction Corporation, 710075 Xi'an, China
机场土基不均匀冻胀变形是机场工程破坏的重要原因之一.因此,在进行机场工程建设之前,必须对机场土基作出冻胀性评价,以便采取有效的防冻胀措施,确保机场工程的安全可靠.土体的冻胀特性一直是国内外研究的焦点,国外学者Everett[1]首先提出毛细理论,对冻胀和冻胀力进行了定量解释和估计,但却不能解释不连续冰透镜的形成原因且低估了细颗粒土中的冻胀压力.认识到了毛细理论的不足,Miller[2]提出在冻结锋面和最暖冰透镜底面存在一个低含水量、低导湿率和无冻胀的带,称为冻结缘.冻结缘理论在一定程度上克服了毛细理论的不足,得到广大学者的认可.这两大冻胀理论的提出为冻胀研究奠定了基础.国内学者吴紫汪[3]对土的冻胀机制、动力及变化规律进行了研究,为道路工程的冻胀成因、分类和病害防治措施的制定提供了理论依据.陈肖柏[4]提出饱水砂砾料冻结时的冻胀敏感性主要受细粒土含量及冻结条件的影响.王天亮等[5]通过葡氏击实和冻胀试验,研究了不同细粒土含量、不同干密度条件下细圆砾土填料的冻胀特性.巨娟丽[6]通过室内试验对白砂岩土的冻胀率冻胀特性进行了研究.程佳等[7]研究了青藏铁路多年冻土区典型土样的冻胀特性.刘新华等[8]研究了季节冻土冻胀和融沉与土质、密度、含水率等性质的关系.高志华[9]选取了21组土样进行分析,从颗粒组成、毛细水上升高度等分析青藏铁路冻胀出现的可能性.张以晨等[10]对5种粗粒土13种不同含泥量土料在不同含水率、饱和度和密实度状态下进行了一系列封闭系统下的冻胀模拟试验.研究了各种粗粒土的η-w关系,并对其进行线性分析,揭示了粗粒土的冻胀规律.徐洪坤等[11]建立了考虑水热耦合迁移的Clausius-Clapeyron方程,推导了机场道基一维垂直向冻胀位移的积分表达式,建立了寒区机场道基冻胀预测模型.杨锐等[12]从能量平衡角度,推导了作用在基层底面的冻胀应力解析式,并在某机场改造工程中作了验算.李博等[13]分析了造成机场冻胀的各种因素,提出了机场工程冻土土基处理的措施.闫永刚等[14]分析了西北壁滩机场道面冻胀产生的原因,提出了消除冻胀的方法.沈哲等[15]指出高寒地区机场土基的冻胀受降温速率、土样的含水率、上覆荷载等因素的影响,并存在复杂的函数关系.
综上研究成果,关于季冻区土基冻胀影响因素和工程实践方面的研究比较少;关于机场冻胀的研究也仅有零星报道,且研究成果比较零散,不成系统,缺乏有效的工程实际价值;而关于砂砾土较多青藏高原季冻区机场冻胀的研究更是未见报道.因此,有必要结合青藏高原季冻区独特的气候和土壤特点,对砂砾土进行冻胀室内试验,研究其冻胀特性并总结规律,结合工程实际提出建议,为青藏高原季冻区机场工程冻害防治提供理论依据.
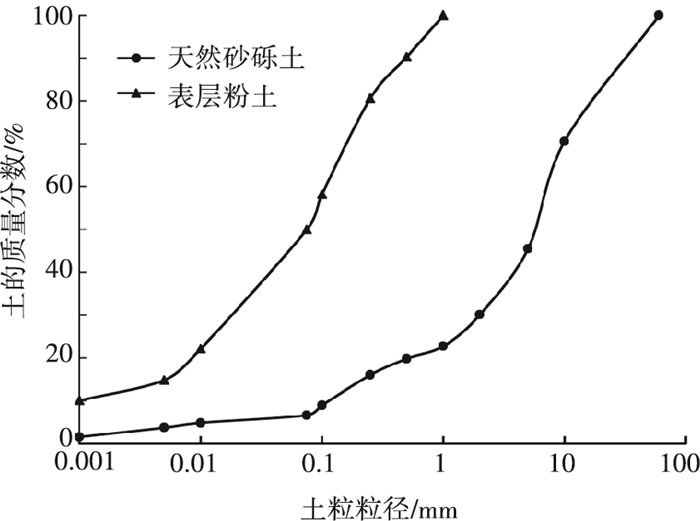
1 概况 1.1 颗粒级配及土样制备试验所用土样取自果洛自治州大武机场现场段,将土样装袋并用货车运送至西安,在实验室内进行过滤杂质、风干等处理.试验土样包括天然砂砾土和表层粉土,天然砂砾土为主要试验对象,表层粉土为对照试验对象.通过筛分试验,测得天然砂砾土中直径小于0.075 mm的颗粒的质量分数(以下简称含泥量)为6.9%,表层粉土的含泥量为50%,将这两种土样按不同的比例掺合均匀,即可得到试验所需的含泥量为10%、15%、20%、25%、45%的土样.已有研究表明,土样颗粒级配对土样的冻胀有明显的影响[10].按公路土工试验规程[16]规定的方法,通过颗粒分析试验得到两种土样的颗粒级配曲线如图 1所示.由图 1可知,天然砂砾土和表层粉土级配良好,属于冻胀敏感性土类.
|
图 1 颗粒级配曲线 |
对含泥量为10%、15%、20%、25%、45%的砂砾土进行标准击实试验,得到不同含泥量下的砂砾土的标准最大干密度和最优含水率如表 1所示.由表可知,砂砾土的最优含水率随着含泥量的增大而增大.然而,砂砾土的标准最大干密度却随着含泥量的增大而减小.
| 表 1 击实试验结果 |
土体的冻胀特性主要用土体的冻胀量和冻胀率表示.冻胀量是地表由于土体冻结而引起的竖向位移,土体在无侧向变形的前提下,经单向冻结,其纵向高度的增量与试样原始高度的比值称为冻胀率(也称冻胀强度或冻胀系数),通常用高度比表示,计算公式为
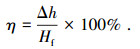
|
(1) |
式中:η为冻胀率%;Δh为冻胀量,mm;Hf为冻结土层的厚度[16].
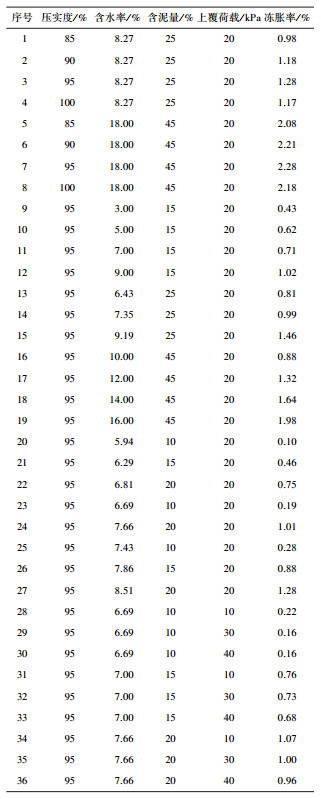
试样制备过程严格按照中华人民共和国行业标准[16]进行.由于原状土样的采取、运输、保存等存在一定的困难,室内试验中采用重塑扰动土样进行冻胀率试验.试验具体方案如表 2所示.
| 表 2 冻胀试验方案 |
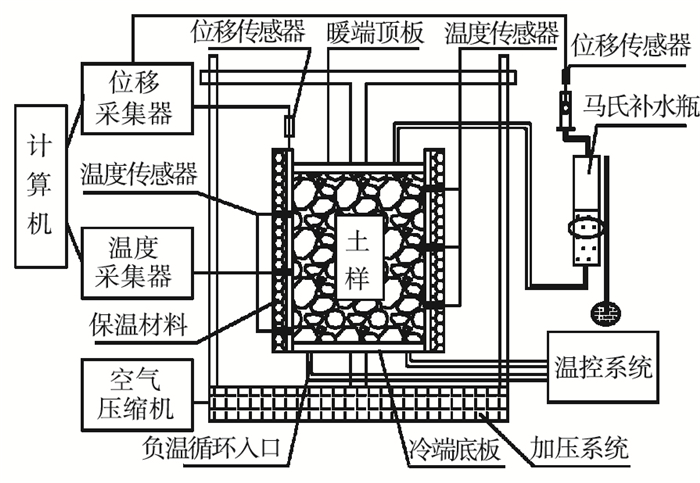
结合砂砾土的特点,本文采用改进的冻胀室内试验装置进行试验.试验装置由试样筒、恒温箱和温控系统、温度检测系统、位移检测系统、数据采集终端、补水系统和气动平衡装置组成,系统图及各组成部分照片分别见图 2、3所示.
|
图 2 冻胀试验装置系统 |

|
图 3 冻胀试验装置系统各组成部分照片 |
由于砂砾土的粒径较大,经过改装后,试样筒由内径15 cm,高16 cm,壁厚1 cm的有机玻璃筒制作,沿高度每隔2 cm设温度传感器插入孔.底板为中空结构,有负温循环液进出口.顶板有外界水源补充通道.
试验步骤如下:1)首先进行击实试验,确定最大干密度和最优含水率,见表 1. 2)冻胀试件成型:在有机玻璃内成型,试样直径15 cm、高13.5 cm.首先按一定的含泥量、含水率配料、闷料24 h,以保证试样的含水率均匀一致,根据压实度称取一定质量,于试样筒中分5层进行击实,静压成型. 3)为防止试验过程中水分流失,在试样顶面和底面各放一张滤纸,然后放上顶板,并稍加力,使土样与顶、底板接触紧密.将两个试样盒放入恒温箱内,试样周侧、底板内放入温度传感器,周侧包裹厚5 cm橡塑海绵保温材料.连接底板冷冻液循环管路及顶板补水管路,供水并排除顶板内气泡,调节供水装置水位.安装位移传感器.将温度和位移传感器与数据采集终端连接. 4)开启加压装置,并调节到所需压力;开启恒温箱及底板冷浴,设定恒温箱为1 ℃,底板冷浴为-15 ℃. 5)试样恒温6 h,并监测温度和变形,待试样初始温度均匀达到1 ℃左右以后,开始冻结. 6)低温恒温循环器调节到-15 ℃并持续0.5 h,让试件迅速从底面冻结,然后底板温度调节到-2 ℃,并以0.2 ℃/h速度下降,保持箱温和顶板温度均为1 ℃.打开电脑上的阿尔泰测控系统读取、保存数据.试验持续至位移量读数恒定不变方可结束(约72 h). 7)试验结束后,迅速从试样盒中取出试样,量测试样高度并测定冻结深度,读取数据并计算结果.
2 试验结果及分析 2.1 典型冻胀过程分析取一组(含水率14%、含泥量45%、压实度95%、上覆荷载20 kPa)试验结果为典型,绘制不同高度处温度随时间的变化关系,如图 4所示.

|
图 4 不同高度处温度随时间变化曲线 |
从图 4中可以看出,不同高度处,土样降温的速率是不同的,其中4 cm处降温速度最快,12 cm处降温速度最慢.同理,绘制冻胀量随时间的变化关系,如图 5所示.

|
图 5 冻胀量随时间变化曲线 |
由图 5可知,土样冻胀基本可以分为4个阶段:1)冻缩阶段.这一阶段内,冻胀率为负值,即土样发生冻缩现象,约4~8 h后土样体积增大,冻胀开始.由于土样颗粒受冷收缩,孔隙水结冰后增大的体积,不足以抵消土样颗粒收缩的体积;水在4 ℃时密度最大,土样所含水分的体积最小,这对于土样的冻缩有一定的影响.此外,给土样加载的20 kPa的上覆荷载,也抑制了土样体积的增长.因此,在起始阶段,土样体积不但不会增大反而会减小.随着温度继续降低,土样开始持续冻胀,当冻胀引起的体积增量超过土样颗粒收缩导致的体积减量时,才能观测到冻胀现象. 2)快速冻胀阶段.这一阶段冻胀量快速增长,是由于此时冰析作用非常强烈,聚集在冻结锋面处的水分冻结成冰时,将挤开土颗粒而形成零散的细小冰透镜体,出现冰分凝现象,因此体积快速增大. 3)缓慢冻胀阶段.这一阶段冰分凝已经比较充分,冻结锋面附近形成的冰透镜的厚度及连续程度加大,使得冻胀量增长的幅度慢慢减小. 4)稳定阶段.这一阶段冻结锋面基本稳定,冰透镜体停止生长,冻胀率几乎停止增长,保持不变状态.
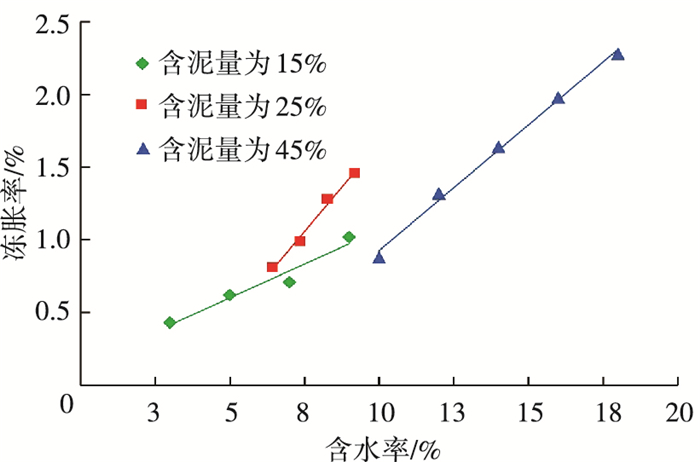
2.2 单因素试验结果与分析 2.2.1 含水率对冻胀率的影响图 6为不同含水率与冻胀率的关系曲线,可以看出,在含泥量一定的情况下,土体的冻胀率随着含水率的增大而增大.其原因分析如下:含泥量一定,则干密度一定,在干密度一定的情况下,土体的饱和度随着含水率的增大相应增大,孔隙中的水分黏结更为紧密,水分连续迁移更加明显,冻结时孔隙冰体积增加,因而产生的总的冻胀量增大.对3组数据拟合可知:土体冻胀率与含水率呈现一元线性关系,3条拟合直线的斜率关系为k0.25>k0.45>k0.15,这是因为含泥量为45%的土样的干密度在3种土样当中最小(见击实试验结果),土体也最疏松,土体有比较大的孔隙,能够容纳更多的冻结冰,不容易使得土粒之间的空间变大从而引起冻胀.此时,随着含水率的增大,冻胀率增大的幅度较小.随着含泥量减小到25%,土样的干密度也相应增大,导致土体颗粒之间的距离相应减小.在这种情况下,薄膜水就会在土体冻结过程中有相对比较活跃的水分迁移.由此冻结的冰能够使得土粒之间的距离明显增大.此时,随着含水率的增大,冻胀率增大的幅度较大.然而这种增幅并非随着干密度的增大一直增大,当含泥量减小到15%时,土体的干密度继续增大,此时冻胀率的增幅反而减小,这是由于此时土体的骨架连结力比较大,这样就会使得存在相互重叠在一起的结合水膜,水膜重叠在一起就会使得这种结合水膜变得比较厚,从而使得水膜的渗透性会相应的降低,最终使得水分迁移的通道也就相对变小了.所以冻胀率的增幅也相应减小.
|
图 6 含水率与冻胀率的关系曲线 |
图 7为不同含泥量与冻胀率的关系曲线,可以看出,在饱和度一定的情况下,土体的冻胀率随着含泥量的增大而增大.含泥量为10%时,土体的冻胀率较小.分析其原因:土颗粒越细,其比表面积越大,表面能越高,与水相互作用的能量也越高.具体来讲,土颗粒表面都会吸附一定厚度的水膜,细颗粒较高的表面能可将水膜紧紧吸附在土粒周围,土粒间的相互连接构成利于水分连续迁移的薄膜通道, 因此,冻胀率更大.

|
图 7 含泥量与冻胀率的关系曲线 |
由上图的拟合曲线斜率的变化可知,冻胀率的增幅随着含泥量的增大呈现减小的趋势,这是由于,随着含泥量的增加,土样当中的细颗粒的含量也在逐渐增加,颗粒直径特别小时,巨大的表面能使得土粒与未冻水的结合作用增大,从而使土粒表面吸附水膜的厚度增大,减小了供水分迁移的薄膜通道,降低了土体的水分渗透性能,甚至土颗粒外围水膜过厚造成叠加完全阻塞迁移通道,从而导致水分迁移能力大大减弱,对冻胀率产生抑制作用.
饱和度越大,冻胀率越大.一是由于饱和度越大,含水率越大,因而冻胀率越大;二是由于饱和度越大,土体当中的孔隙体积占土体总体积的比例就越小,冻结期间更容易被冻结冰填充,从而更容易引起土颗粒位移,产生更大的冻胀.同时观察3条曲线的斜率可得,冻胀率的增幅随着饱和度的增大呈现减小的趋势,这是因为未饱和时,水分的迁移和聚集作用比饱和时更加明显,因而对于冻胀增幅的抑制作用小.
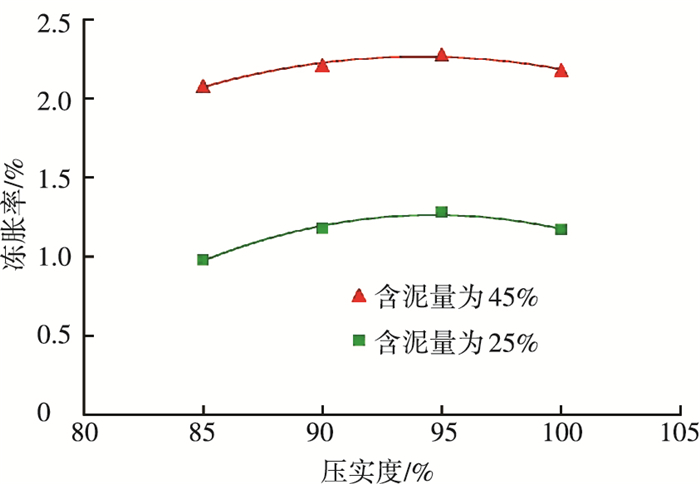
2.2.3 压实度对冻胀率的影响图 8为不同压实度与冻胀率的关系曲线,可以看出,在土体含水率和含泥量相同的条件下,土体的冻胀率随着压实度的增大呈现增大后减小的趋势.其原因分析如下:在压实度较低时,随着压实度的增大,土中未冻水膜的连续性比疏松时未冻水膜的连续性增强,有利于水分迁移与聚冰,因而冻胀强度增大;当压实度增大到一个临界值时使薄膜通道减到最小,此时土体的冻胀强度最大,而随着压实度继续增大超过这一临界值时,土体的冻胀强度减小,这是由于土中孔隙体积缩小,使得土颗粒间的有效接触面积增加,造成外围水膜相互叠加,导致冻结时水分迁移受阻.
|
图 8 压实度与冻胀率的关系曲线 |
在工程实际中,一般将压实度控制在95%~98%的范围内,而实验结果表明,压实度为95%左右时,冻胀率达到最大值,因此在实际施工时,对压实度的控制应予以注意.
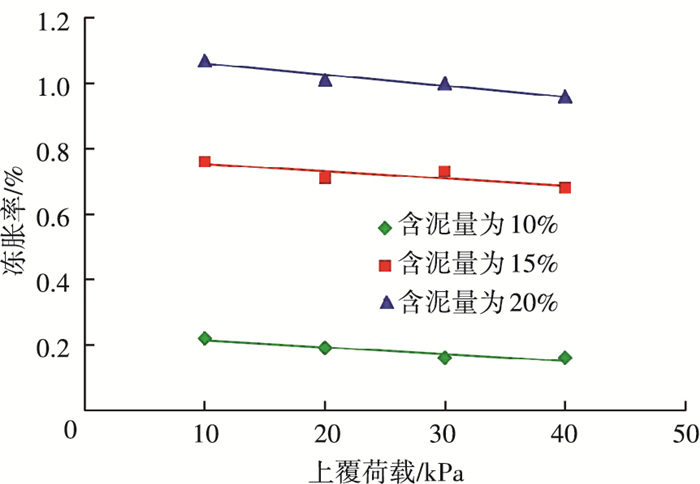
2.2.4 上覆荷载对冻胀率的影响图 9为不同上覆荷载与冻胀率的关系曲线,可以看出,上覆荷载对土样的冻胀具有抑制作用,冻胀率随上覆荷载的增大而减小.但是从拟合曲线的变化率来看,这种抑制作用影响不大,这是由于土体内部冻胀时所产生的冻胀力是非常大的,外加荷载相对来说所起的作用就比较小了.
|
图 9 上覆荷载与冻胀率的关系曲线 |
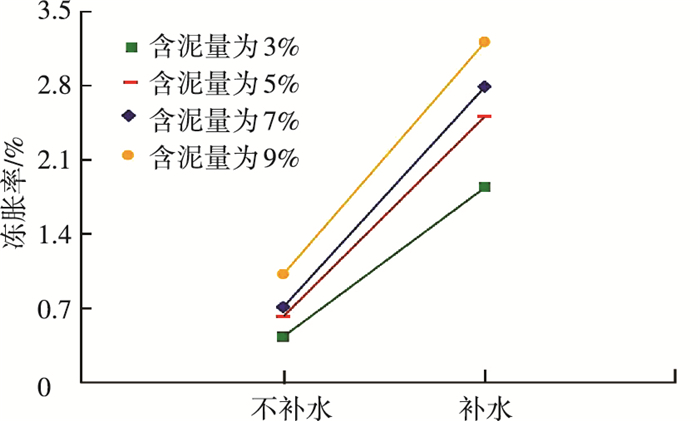
图 10为是否补水与冻胀率的关系曲线,可以看出,是否补水对土样的冻胀率影响较大,补水能使冻胀率增大3倍以上,这是由于土体内部水分迁移聚集形成孔隙负压,使得外界水分源源不断地向冻结封面迁移和聚集,并形成冰透镜体,导致冻胀率急剧增大,这说明外界补水是引起及土基冻胀的主要因素.
|
图 10 是否补水与冻胀率的关系曲线 |
将试验数据结果整理如表 3所示,以含水率ωm、含泥量ωs、压实度k、上覆荷载p为自变量,以冻胀率η为因变量.利用MATLAB编程对试验结果进行多元回归分析,得到含水率、含泥量、压实度、上覆荷载综合影响下的冻胀率的回归模型为

|
| 表 3 冻胀试验结果汇总 |
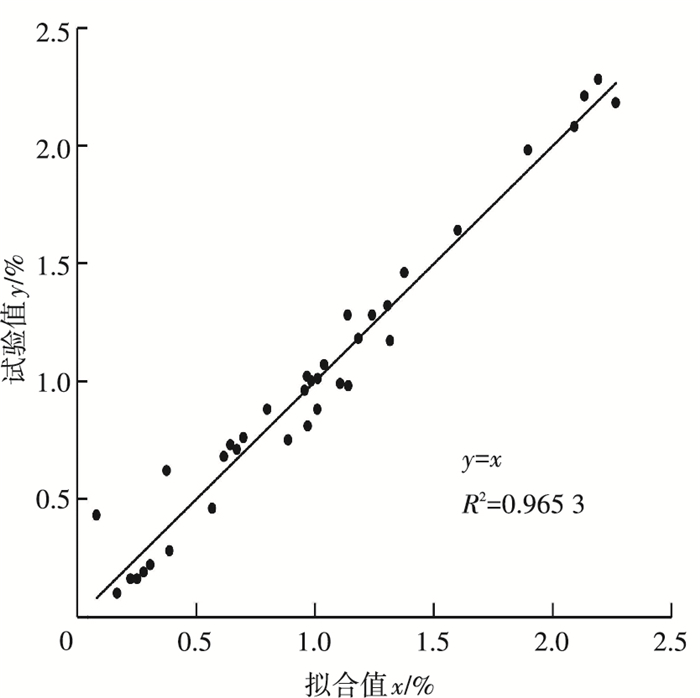
修正拟合系数R2=0.990 872,F=542.758 6>F0.05(4,36)=2.65,显著性非常好,反映该回归模型拟合情况良好,可信度较高,说明以上几个因素对土体冻胀率有显著性影响,故该回归模型合理有效.由各个因素回归系数的可知,对冻胀率的影响由大到小的顺序:含水率、含泥量、压实度、上覆荷载.为了检验该公式的正确性和有效性,本文将初始条件代入公式,得到冻胀率拟合值,将其与试验值对比分析如图 11所示.
|
图 11 试验值与拟合值对比 |
由图 11可知,计算值与试验值拟合情况良好,说明该公式具有较高的准确性和一定的有效性.应用该回归模型可以预测不同因素综合影响下的冻胀率,具有一定的工程应用价值.由于该公式只是考虑到了压实度、含水率、含泥量、上覆荷载等几种主要因素对于冻胀率的影响,并未将其他所有因素考虑在内,因此还具有一定的局限性,这一点有待进一步改进.
4 结论1) 在封闭条件下,冻胀率随含水率的增大而线性增大;随含泥量的增大呈非线性关系递增;随压实度的增大呈先增大后减小的趋势,在压实度为95%的状态下达到最大值;随上覆荷载的增大呈线性关系平缓递减.
2) 经多元回归分析,得到了多因素综合影响下的回归模型为η=0.147 651ωm+0.121 521ωs-0.002 08ωs2-0.048 18k+0.000 323k2-0.002 74p.可见含水率ωm和含泥量ωs对冻胀的影响较大.应用该回归模型可以预测不同因素综合影响下的冻胀率,具有一定的工程应用价值.
3) 外界补水条件下,土体冻胀率显著增大,通常能够增大3倍以上.
4) 各个因素对冻胀率的影响由大到小顺序:补水、含水率、含泥量、压实度、上覆荷载.因此,在工程实际中,控制补水、含水率、含泥量是防冻设计的关键.
| [1] |
EVERETT D H. The thermodynamics of frost damage to porous solids[J]. Transaction Faraday Society, 1961, 57: 1541-1551. DOI:10.1039/tf9615701541 |
| [2] |
MILLER R D. Lens initiation in secondary frost heaving[R]. Lulea, Sweden: Int Symp on Frost Action in Soils, 1977.
|
| [3] |
吴紫汪. 土的冻胀性试验研究[M]//兰州冰川冻土所集刊第2号. 北京: 科学出版社, 1981: 82-96.
|
| [4] |
陈肖柏. 砂砾料之冻胀敏感性[J]. 岩土工程学报, 1988(3): 23-29. |
| [5] |
王天亮, 岳祖润. 细粒含量对粗粒土冻胀特性影响的试验研究[J]. 岩土力学, 2013, 34(2): 359-365, 388. |
| [6] |
巨娟丽. 白砂岩土的冻胀率试验研究[J]. 水利与建筑工程学报, 2004, 2(2): 51-54. |
| [7] |
程佳, 赵相卿, 杨晓明. 青藏铁路多年冻土区典型土样冻胀率特性研究[J]. 冰川冻土, 2011, 33(4): 863-866. |
| [8] |
刘新华. 季节冻土冻胀和融沉的影响因素研究[D]. 西安: 长安大学, 2007.
|
| [9] |
高志华. 青藏铁路路基冻胀变形特点研究[D]. 西安: 长安大学, 2010. http://kns.cnki.net/KCMS/detail/detail.aspx?filename=tdjz201006037&dbname=CJFD&dbcode=CJFQ
|
| [10] |
张以晨, 李欣, 张喜发, 等. 季冻区公路路基粗粒土的冻胀敏感性及分类研究[J]. 岩土工程学报, 2007, 29(10): 1522-1526. DOI:10.3321/j.issn:1000-4548.2007.10.015 |
| [11] |
徐洪坤, 杨祺, 伍危. 寒区机场道基冻胀预测模型[J]. 路基工程, 2007(5): 17-19. |
| [12] |
杨锐, 王肖戎, 许金余. 高寒地区机场道面基层底面冻胀应力的计算[J]. 空军工程大学学报(自然科学版), 2007, 8(3): 16-18. |
| [13] |
李博, 蔡良才, 张罗利. 机场工程土基处理分析[J]. 四川建筑科学研究, 2010, 36(6): 104-106. |
| [14] |
闫永刚, 刘文录. 西北戈壁滩机场水泥混凝土道面病害与对策研究[J]. 甘肃科技纵横, 2010, 39(3): 151-154. |
| [15] |
沈哲, 李永毅, 李澎, 等. 高寒地区机场土基冻胀特性试验研究[J]. 施工技术, 2010, 39(增刊): 8-11. |
| [16] |
交通部公路科学研究院. 公路土工试验规程: JTG E40-2007[S]. 北京: 人民交通出版社, 2007: 345-349.
|
 2016, Vol. 48
2016, Vol. 48