2. 北京交通发展研究中心, 100055 北京
2. Beijing Transportation Research Center, 100055 Beijing, China
随着经济快速发展和城市化进程加快,我国大城市交通拥堵问题日益突出.解决交通拥堵问题的首要环节是准确认识交通拥堵状况,如何建立交通运行状况监测评价系统已成为亟待解决的问题.近年来,北京、杭州、深圳等大城市在该领域进行了广泛研究,其中,交通指数[1]是基于浮动车数据综合反映道路运行状况的指标,公交指数[2]是基于公交运行数据综合反映公交运行情况的指标,包括公交车所在道路拥堵程度、公交车方便舒适性等.目前对交通指数和公交指数各自的分析研究较多,虽然二者都对道路交通运行情况有所反映,但是,单独任何一者都不能全面评价道路交通运行情况.又由于缺乏对交通指数与公交指数的关联性分析,二者只能各自孤立发挥评价作用,无法互相评估、预测,利用二者的联系构建综合交通运行指标体系、多方式交通运行监测系统等更是难以开展.因此,为构建多方式交通运行综合监测与评价系统,交通指数和公交指数关联性分析已成为迫在眉睫的学术问题.尽管侧重点不同,但交通指数和公交指数均在不同程度上反映道路运行状况.二者的关联性特点与不同股票市场的股票价格指数的关联性特点具有较强的相似性.国内学者对股票价格指数关联性的分析多采用计量经济学方法[3-5].因此,本文拟采用格兰杰因果检验、协整检验、VAR(向量自回归模型)模型、VEC(向量误差修正模型)模型等计量经济学方法,探究北京市二环内交通指数和公交指数短期相关性和长期均衡关系,二者变化趋势的协同关系将丰富现有多方式交通运行监测系统,并将为构建以二者关联性关系为基础的多方式交通运行评价体系提供理论依据.
1 交通指数和公交指数 1.1 交通指数交通指数是综合反映道路网拥堵程度的概念性指数,在国内外已有成功应用的经验.交通指数根据所在城市实际特点进行定义和计算.德州交通研究所于1994年提出道路拥堵指数描述交通相对拥堵程度[6];北京市采用拥堵里程比例概念,建立指数计算模型[1];上海则采用机动车运行速度和道路饱和度等指标综合计算得到城市交通拥堵指数.北京市交通指数的计算过程如下[1]:1)首先由车辆位置数据和GPS数据处理得到不同功能等级道路的平均行程速度vk;2)根据不同等级道路处于严重拥堵等级的速度阈值vm,统计其处于严重拥堵运行等级的路段里程比例,i等级道路严重拥堵里程比例Ci计算公式为
由交通指数的计算过程可以看出,北京交通指数主要受到不同等级道路严重拥堵道路里程比例和VKT的影响,即受到道路平均行程速度和流量的影响.显然,随着路网拥堵严重程度的上升,交通指数会随之上升,二者存在正相关关系.
1.2 公交指数公交指数是评价地面公交运行状况概念性评价指标,其评价标准包括拥堵程度与等候时间等5个方面,不少研究中已经据此建立了公交便利指数、公交快捷指数、公交可靠指数等计算模型反映公交运行情况[7].针对北京市公交运行实际情况,本文中公交指数重点考虑公交运行的方便快捷性和方便舒适性.
1.2.1 公交运行快捷性指数计算基于公交IC卡数据、公交GPS等数据,以公交客运周转量比例为权重,对公交运行速度进行集成计算获得.其计算方法为[8]
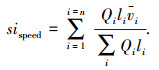
|
其中:vi为站段i的公交平均运送速度,vi= 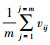
以公交客运周转量比例为权重,对公交车内乘载率进行集成计算获得.其计算方法为[7]
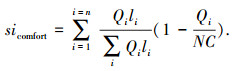
|
其中:Qi为站段i的断面客流量;li为站段i的里程;Qi与li之乘积为站段i的客运周转量;N为统计时段内经过站点i的车次数;C为车辆座位数.
在此基础上,基于北京市的公交运行现状数据,根据公交线路类型的不同进行公交运行快捷性指数和公交运行方便舒适性指数阈值划分,经归一化得到0~10的指数指标值;以权重系数法,集成计算公交运行快捷性指数与公交运行方便舒适性指数,获得公交指数.
由北京公交指数的计算过程可以看出,公交指数主要受到运行速度和客运周转量的影响,另外也考虑了车辆满载率.当交通拥堵发生时,路网的运行效率会出现明显下降,受其影响,公交运行速度和客运周转量都会降低,从而引发公交指数的负变化.
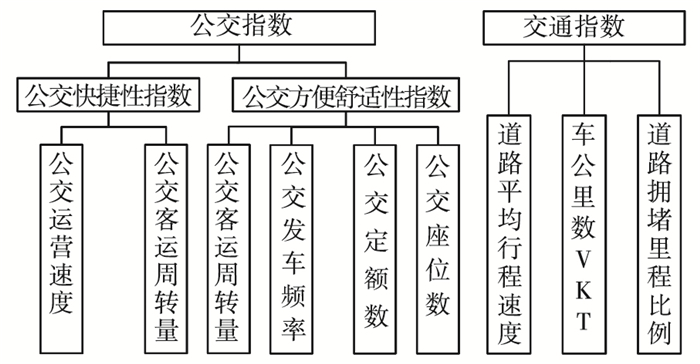
1.3 交通指数和公交指数对比分析通过对交通指数和公交指数的分析,发现二者在数据来源、评价重点、分级标准、加权权重和结构组成等方面有所不同,交通指数数据来源是浮动车数据,而交通指数数据来源是公交IC卡数据和GPS数据;交通指数评价重点是小汽车运行状况,公交指数主要是评价地面公交运行状况;交通指数计算过程中分级标准是参照道路功能等级,加权权重是车公里数(VKT),而公交指数是参照公交线路等级,加权权重是公交客运周转量;二者结构组成如图 1所示.
|
图 1 交通指数与公交指数结构组成对比 |
虽然交通指数和公交指数在上述几方面有所差异,但二者在评价重点对象运行环境、计算公式等方面相互关联.由于二者评价重点对象(小汽车和公交车)在同一路网,均受到道路运行条件影响,且二者在不同程度上反映道路运行情况;由交通指数和公交指数计算公式可知,二者大小都受运行速度影响,小汽车和公交车运行速度与整个路网运行速度密不可分,且小汽车和公交车运行速度相互影响.
因此,本文将对交通指数和公交指数的关联性进行分析,通过研究交通指数和公交指数的关联性,为基于二者关联性构建区域多方式交通出行指数,进行多方位交通运行监测奠定基础.
2 交通指数与公交指数关联性分析方法计量经济学方法适用于时间序列的相关性分析,并广泛应用于经济学领域,如股票价格指数序列相关性分析、货币供应量与外汇储备相关性分析[9]等.交通指数和公交指数的关联性特点与不同股票市场的股票价格指数的关联性特点具有较强相似性,具体表现在以下几个方面:1)时间序列特点相似.可将一定时期内交通指数和公交指数视为两个时间序列,且此两种时间序列与股票价格指数具有相似特性,如连续性、复杂性、动态性、非平稳性等. 2)均可反映总体情况.尽管侧重点不同,交通指数和公交指数均在一定程度上反映道路交通运行状况,相比而言,股票价格指数从总体上反映股票市场行情. 3)数据来源相互联系.股票价格指数来自不同股票市场,不同市场间彼此联系,投资资金在市场之间流动性较好,共同信息所引起的不同市场收益率的变化也极为相近;而交通指数和公交指数分别以小汽车和公交车为数据来源,小汽车和公交车在行驶中也会互相影响. 4)存在共同影响因素:不同股票市场受到国家经济政策、市场管理制度等因素共同影响,与此类似,小汽车与公交车的行驶状况也均受道路条件、道路交通状况、道路管理措施等因素共同影响.
本文因此借鉴计量经济学中时间序列分析法,对交通指数和公交指数短期和长期关联性进行分析.其中,短期是指路网布局、公交线路等因素保持不变(即存在不可变因素)对应的时期,长期则是路网布局、公交线路、机动车保有量、道路管理措施等因素发生改变对应的时期.本文按照对交通指数序列和公交指数序列进行时间序列平稳性检验→格兰杰因果检验→建立VAR模型→协整检验→建立VEC模型的技术路线进行分析.其中,时间序列平稳性检验是交通指数和公交指数关联性分析的前提,格兰杰因果检验目的是检验交通指数和公交指数是否具有格兰杰因果关系,判断二者是否能够相互预测;建立VAR模型目的是明确交通指数和公交指数的短期相关性的数量关系,若二者存在短期相关性的数量关系,则交通指数和公交指数可在短期内根据数量关系相互预测,这将有助于完善多方式交通运行监测评价系统;协整检验目的是明确交通指数和公交指数是否具有相同的随机性趋势及长期均衡关系;最后,建立VEC模型的目的是检验交通指数和公交指数长期协整关系是否显著,若二者长期协整关系显著,则说明二者关系不受路网布局、公交线路、机动车保有量、道路管理措施等变化的影响,可长期通过二者数量关系相互预测,利于长期量化监测,建立长期稳定的多方式交通运行监测评价系统.
3 交通指数与公交指数关联性分析以北京市二环内连续一周交通指数和公交指数为例进行关联性分析,分析时段为6:00—21:30,以30 min为时间步长构成数据量均为224条的交通指数序列和公交指数序列,如图 2所示.

|
图 2 交通指数与公交指数时变 |
为避免时间序列出现伪回归问题,需利用ADF检验(augment dickey-fuller test)对时间序列进行平稳性检验.通过ADF检验,得到交通指数序列的一阶差分序列和公交指数序列的一阶差分序列均为平稳序列,两序列均为一阶单整序列,即服从I(1).
3.2 基于格兰杰因果检验的指数关系格兰杰因果关系,即某时间序列变量变动,另一个时间序列变量会发生一致的可预测变化[10].通过格兰杰因果关系检验,判断交通指数和公交指数中,一个指数的变化是否会引起另一个指数的变化.
为避免虚假回归问题,需保证进行格兰杰因果关系检验的时间序列具有平稳性.由时间序列平稳性检验可知,交通指数和公交指数序列均为一阶单整,因此格兰杰因果检验是对交通指数序列Y和公交指数序列X一阶差分后的序列DY和DX进行检验.利用计量经济学分析软件Eviews6.0(econometrics views6.0)进行格兰杰因果检验,检验结果显示,在5%显著水平下,能够拒绝原假设:DX不是DY的格兰杰原因,DY不是DX的格兰杰原因.因此,交通指数和公交指数互为格兰杰原因,即交通指数和公交指数能够相互解释将来的变化.由于交通指数的数据来源小汽车和公交车都行驶在北京二环内道路上,都受到二环内道路路况的影响,且小汽车和公交车存在相互影响,这是导致二者互成格兰杰因果关系的可能原因.
3.3 基于VAR模型的指数间短期相关性分析为明确交通指数和公交指数的短期相关性的数量关系,建立VAR模型. VAR模型用来估计联合内生变量的动态关系,而不带有任何事先约束条件.
VAR模型的一般形式为
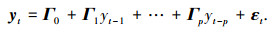
|
其中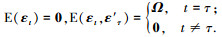
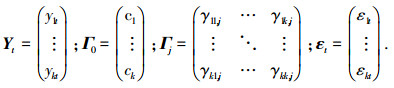
|
其中:T为观测值的数目,t∈T;Yt为k维内生变量(向量);Γj为k×k维系数矩阵;εt为k维随机向量,p为内生变量的滞后阶数.
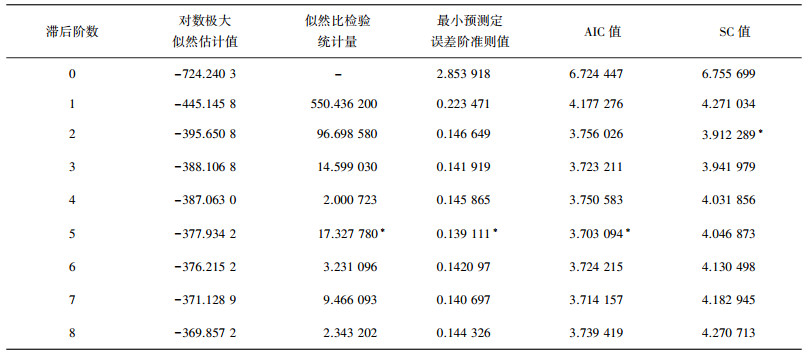
3.3.1 确定VAR模型内生变量滞后阶数确定模型内生变量滞后阶数p的大小一般采取AIC准则(Akaike info criterion)和SC准则(Schwarz criterion)[11].利用Eviews6.0进行计算,结果如表 1所示,以*号最多的阶数确定滞后阶数,可以看出该VAR模型的滞后阶数p为5.
| 表 1 VAR模型滞后阶数确定 |
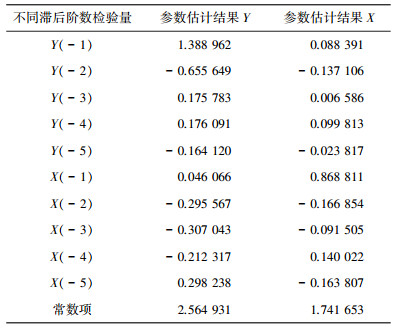
基于交通指数、公交指数数据和滞后期p,计算得到VAR模型参数估计结果如表 2所示.
| 表 2 VAR模型参数估计 |
由表 2中各参数估计结果得到VAR模型如下式所示.
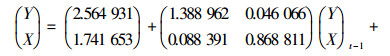
|

|
作为对模型的整体检验,模型估计的拟合优度值R2能解释因变量的变化的百分数,VAR模型估计的R2为0.889与0.636,拟合优度值较高,这表明模型的拟合度良好.
3.3.3 VAR模型稳定性分析当把一个脉冲冲击施加在VAR模型中某一个方程过程上时,随着时间的推移,如果冲击消失,系统是稳定的,否则,系统是不稳定的[10].为验证交通指数和公交指数短期关联性是否稳定,需对VAR模型进行稳定性分析.
对于VAR(p),yt=Γ0+Ayt-1+…+εt,模型稳定的条件是特征方程|A-λI|=0的根的模都小于1.由3.3.1节得VAR模型滞后阶数为5,且具有2个内生变量,因此,模型有10个根,单位根分析结果如表 3所示,根的模均小于1,表明估计的VAR模型是稳定的.
| 表 3 VAR模型单位根分析结果 |
上述分析表明交通指数和公交指数在短期内存在稳定的相关关系,即交通指数和公交指数在路网布局、公交线路等因素没有改变时,二者具有一致性变化趋势.交通指数和公交指数都从总体上反映路网运行状况,当上述因素保持不变时,二者对于同一路网的道路拥堵程度的描述具有一定一致性,这符合二者的交通意义.
3.4 基于协整检验的指数间长期均衡关系为明确交通指数和公交指数的长期均衡关系,需要进行协整检验,建立VEC模型.由于VEC模型是有协整约束(即有长期稳定关系)的VAR模型,用于具有协整关系的非平稳时间序列建模,因此在估计VEC模型前需进行Johansen协整检验,并要确定协整关系的数量.
3.4.1 协整检验协整即存在共同的随机性趋势,协整检验的目的是决定一组非平稳序列的线性组合是否具有稳定的均衡关系.由VAR模型可知,交通指数和公交指数存在短期内的相关关系,下面则通过Johansen协整关系检验[12]以及VEC模型对二者长期均衡关系进行分析.结果见表 4,检验结果中包含(迹统计量和最大特征值统计量)两种类型检验统计量的检验结果.
| 表 4 Johansen检验结果(5%显著水平) |
在迹统计量检验中,在原假设“存在0个协整关系”下,迹统计量为21.536,迹统计值大于5%显著水平的临界值12.320,因此拒绝原假设.而在原假设“至多存在一个协整关系”下,迹统计值小于5%显著水平的临界值,不能拒绝原假设.同理,在最大特征值统计量检验中,拒绝“存在0个协整关系”的原假设,不能拒绝“至多存在1个协整关系”的原假设.上述迹统计量检验表明,交通指数和公交指数在5%显著水平上存在一个协整关系,即二者存在共同的随机性趋势.
3.4.2 VEC模型建立基于长期协整关系,建立VEC模型.如果Y包含的k个序列之间存在协整关系,根据Johansen协整检验方程,VEC模型可以写为
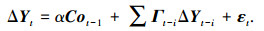
|
(1) |
式(1)中的每一个方程都是一个误差修整模型,其中ΔYt=Yt-Yt-1;Cot-1是误差修整项,反映变量间的长期均衡关系;α反映变量之间的均衡关系偏离长期均衡状态时,将其调整到均衡状态的调整速度.
由3.4.1可知,交通指数和公交指数存在协整关系,据此计算得到VEC模型为

|
其中Cqt-1=Yt-1+246.956 3+Xt-1-1 150.168.
模型估计的拟合优度值R2=0.429,0.295,拟合优度值偏低,表明交通指数和公交指数的长期均衡关系并不显著,即当路网布局、公交线路、道路管理措施等因素发生改变时,交通指数和公交指数关联性减弱,这可能是由于当上述因素(例如开设公交专用道)发生变化时,小汽车和公交车相互影响减弱,交通指数和公交指数对于同一路网的道路拥堵程度的描述产生差异.
4 结论1) 利用格兰杰因果检验、VAR模型、Johansen协整检验和VEC模型得出了目前北京市二环内交通指数和公交指数存在关联关系,丰富了多方式交通运行监测系统,为进行多方式多方位交通运行评价奠定基础.
2) 交通指数和公交指数在短期内存在相关关系,表明在路网布局、公交线路等因素保持不变时,交通指数和公交指数有较一致的变化趋势.交通指数与公交指数存在即时的联系,交通指数有助于预测公交指数,公交指数也有助于预测交通指数.交通指数和公交指数间存在共同的随机性趋势,但交通指数和公交指数长期均衡关系不显著,在短期联动效应消退后,两序列仍保持着相对独立,这表明在路网布局、公交线路等因素发生改变时,交通指数和公交指数间的一致性会减弱.
3) 交通指数和公交指数在短期内能够相互预测,可据此丰富现有的多方式运行监测系统.当路网布局、公交线路、道路管理措施等因素不变时,利用二者较一致的变化趋势,可使二者互为补充,构建多方式交通运行评价体系.然而,当路网布局等因素发生改变时,交通指数和公交指数的一致性减弱,此时,综合交通运行监测评价系统应重新慎重评估二者的关系.
| [1] |
扈中伟, 孙建平, 温慧敏. 北京市交通拥堵评价实证研究[C]//第十六届海峡两岸都市交通学术研讨会论文集. 南京: 江苏省科学技术协会, 2008: 219-224. http://www.wanfangdata.com.cn/details/detail.do?_type=conference&id=6795366
|
| [2] |
蒋新. 基于多源数据的大城市常规公交运行评价研究[D]. 北京: 北京交通大学, 2011. http://cdmd.cnki.com.cn/Article/CDMD-10004-1011092716.htm
|
| [3] |
宋琳, 应晓芸. 货币供应量与我国股票指数关系的实证研究[J]. 山东财政学院学报, 2013(2): 11-22. |
| [4] |
李姝, 吕光明. 中国股市股价指数变动的协整研究[J]. 辽宁师范大学学报(社会科学版), 2001, 24(5): 33-35. |
| [5] |
彭明旭. 沪深股市收益和风险分析[J]. 经济研究导刊, 2011(10): 76-77. DOI:10.3969/j.issn.1673-291X.2011.10.033 |
| [6] |
SCHRANK D, LOMAX T. 2001 urban mobility report[M]. Texas: Texas Transportation Institute, 2001.
|
| [7] |
闫卫坡. 大城市公共交通出行指数分析研究[D]. 北京: 北京工业大学, 2012. http://cdmd.cnki.com.cn/Article/CDMD-10005-1012037355.htm
|
| [8] |
闫卫坡, 翁剑成, 荣建, 等. 公共交通快捷指数分析模型研究[J]. 交通运输系统工程与信息, 2012, 12(3): 165-169. |
| [9] |
池启水. 外储备增加对基础货币投放的影响[J]. 数理统计与管理, 2008, 27(4): 686-694. |
| [10] |
潘省初. 计量经济学[M]. 4版. 北京: 中国人民大学出版社, 2012.
|
| [11] |
顾剑华. 政府公共支出对GDP长期增长效应的动态分析:基于广西数据的协整检验和VAR模型分析[J]. 工业技术经济, 2007, 26(11): 42-47. DOI:10.3969/j.issn.1004-910X.2007.11.012 |
| [12] |
CAVALIERE G, RAHBEK A, TAYLOR R. Testing for cointegration in vector autoregressions with non-stationary volatility[J]. Journal of Econometrics, 2010, 158(1): 7-24. DOI:10.1016/j.jeconom.2010.03.003 |
 2016, Vol. 48
2016, Vol. 48