2. 吉林省道路交通重点实验室(吉林大学), 130022 长春;
3. 山东理工大学 交通与车辆工程学院, 255000 山东 淄博
2. Key Laboratory of Road Traffic in Jilin Province(Jilin University), 130022 Changchun, China;
3. School of Transportation and Vehicle Engineering, Shandong University of Technology, 255000 Zibo, Shandong, China
交通冲突技术是当前道路交通安全评价方法的主流[1],许多专家学者对其进行了广泛关注和深入研究,并在常规交通冲突判别指标方面取得了丰硕的研究成果[2-5].但是,多年前已被广泛认可的道路交通设计理论指出要以道路使用者的交通需求和生理-心理反应特征作为道路设计的理论基础[6],而当前的道路交通安全评价技术特别是交通冲突技术并未从驾驶人心理角度对道路交通状况进行安全性评价,究其原因是未找到反映驾驶人心理负荷的交通冲突量化指标以及基于该指标的交通冲突辨识方法.外界刺激与瞳孔直径的关系研究为寻找可反映驾驶人心理负荷的交通冲突量化指标提供了新的方向:裴玉龙等[7]研究了酒精刺激对驾驶人瞳孔直径的影响;Neumann D L等[8]研究了精神负荷对瞳孔直径变化的影响;Einhäuser W等[9]研究了知觉变化对瞳孔直径的影响并分析了引起瞳孔直径变化的生理因素;Stuart R Steinhauer等[10]从神经层面分析了任务难度对瞳孔直径的影响规律;Barry Winn等[11]研究了年龄、性别等因素对光照刺激下瞳孔直径变化的影响;Marco Pedrotti等[12]研究了声音等刺激因素造成的心理压力及其导致的瞳孔直径变化.
上述研究成果未面向交通冲突刺激对驾驶人瞳孔直径的影响进行研究,因此本文拟通过相关分析明确以撞固定物冲突[13-14]为代表的交通冲突刺激对驾驶人瞳孔直径的影响,在此基础上研究面向道路交通安全评价需求的交通冲突快速识别方法.
1 数据的采集与处理 1.1 试验数据采集使用驾驶模拟器对机动车、道路环境和固定障碍物进行撞固定物冲突的室内情景仿真.模拟试验车型为捷达轿车,路面类型为沥青路面,道路线形为直线,道路长度为115 m,为便于试验环境的量化并排除碰撞角度等因素的影响,将固定障碍物设置为驾驶训练场内的高墙.设置直线加速距离为100 m,制动位置到固定障碍物的距离为15 m.试验场景示意图如图 1所示.
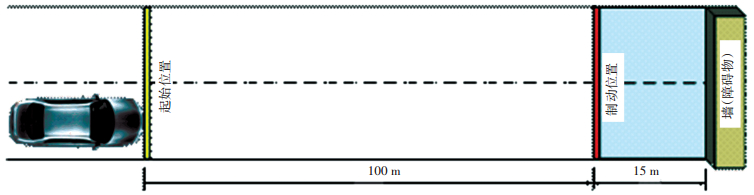
|
图 1 试验场景示意图 |
选择驾龄超过20 a的6位男性驾驶人作为试验对象,调节室内照度,首先要求驾驶人分别在370 lx和490 lx的平均照度下静止注视试验场景,然后要求驾驶人在370 lx和490 lx的平均照度下驾驶捷达轿车在100 m直线道路内从起始位置由静止分别加速到20、30、40 km/h,越过制动位置后自由制动,重复试验10次.使用Smart Eye Pro 5.7眼动仪以60 Hz的采样频率采集驾驶人瞳孔直径数据,使用TES-1339R照度计及其电脑端软件同步记录驾驶人位置处的照度数据.按照度将试验数据分为370 lx照度下的L组和490 lx照度下的H组,记370 lx照度下的静止注视、20 km/h、30 km/h、40 km/h试验数据分别为L0、L1、L2、L3,记490 lx照度下的试验数据分别为H0、H1、H2、H3.
1.2 试验数据处理首先剔除眨眼时的瞳孔直径数据.根据眼动仪提供的同步眨眼数据blink,剔除blink不为0帧号(framenumber)所对应的瞳孔直径数据.未剔除眨眼噪声的瞳孔直径曲线如图 2所示,眨眼噪声剔除后的瞳孔直径曲线如图 3所示.
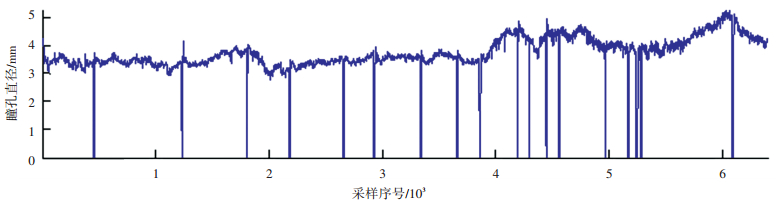
|
图 2 未剔除眨眼噪声的瞳孔直径曲线 |
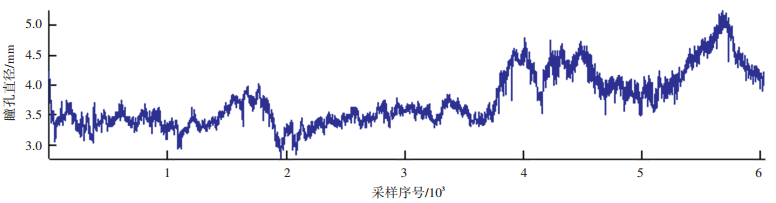
|
图 3 眨眼噪声剔除后的瞳孔直径曲线 |
为在后续研究中可更有效地分析瞳孔直径的变化特征,并降低交通冲突识别的计算成本,有必要对瞳孔直径数据进行基于离散小波变换的降噪处理[12].使用Haar小波基进行5级小波变换并重构后的部分瞳孔直径曲线如图 4所示.
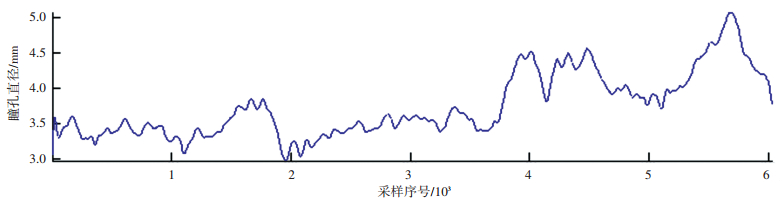
|
图 4 5级小波(Haar)分解的瞳孔直径曲线 |
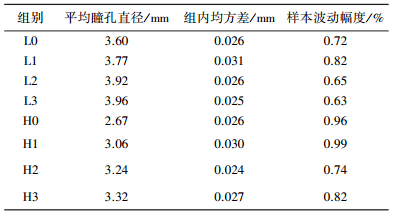
根据照度和冲突程度的不同,可将试验数据分为L0、L1、L2、L3、H0、H1、H2、H3共8组,每组试验包含60个样本数据,以每个样本的均值作为组内单元值求得的组内方差见表 1.
| 表 1 试验数据组内方差表 |
由表 1可见,每组中各样本均值相对每组样本总数的平均值,其波动幅度均未超过1.00%,说明组内样本差异不大,驾驶人个体区别未显著影响试验数据的稳定性.
2 瞳孔直径与撞固定物冲突的相关性分析 2.1 瞳孔直径与照度的相关性分析为确定照度对瞳孔直径的影响程度,需进行照度与瞳孔直径的相关性分析.首先分析L组和H组的平均照度与平均瞳孔直径的相关性.
设每组第i个样本的平均瞳孔直径值为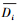
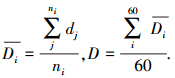
|
(1) |
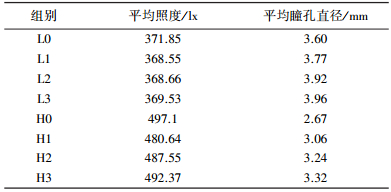
| 表 2 照度与瞳孔直径均值表 |
经计算,平均照度与平均瞳孔直径的相关系数为-0.89,属于高度负相关.
为明确照度波动对瞳孔直径的影响,需分析每组照度数据与对应瞳孔直径的相关性.部分照度与对应瞳孔直径的曲线如图 5.
|
图 5 照度曲线与瞳孔直径曲线 |
经计算,L0、L1、L2、L3各组照度与瞳孔直径的相关系数分别为-0.247、-0.033、-0.091、-0.188,最大照度差分别为3.62、4.02、4.45、5.49 lx;H0、H1、H2、H3各组照度与瞳孔直径的相关系数分别为-0.050、-0.067、-0.297、-0.075,最大照度差分别为4.00、5.47、5.64、5.89 lx.
各组中照度与瞳孔直径的相关系数绝对值均未超过0.30,属于微相关.平均照度与平均瞳孔直径的相关性明显,而未取均值的照度与瞳孔直径仅为微相关.
2.2 瞳孔直径与交通冲突的相关性分析设起始位置到制动位置时间内驾驶人接受的刺激为0,制动位置后至车辆停止时间内冲突对驾驶人的刺激为1,构造冲突刺激曲线,计算冲突刺激与瞳孔直径的相关系数. L1、L2、L3各组冲突刺激与瞳孔直径相关系数分别为0.64、0.64、0.77,H1、H2、H3各组冲突刺激与瞳孔直径相关系数分别为0.94、0.81、0.77.
由各组相关系数可见,相关系数均在0.64以上,属于显著相关范围,说明冲突刺激对驾驶人瞳孔直径产生了明显的影响,通过瞳孔直径识别交通冲突具有可行性.
3 基于瞳孔直径的交通冲突快速识别方法 3.1 GSA原理与优势万有引力搜索算法(GSA)[15]假设搜索粒子在空间中具有一定质量且遵循万有引力定律和动力学定律,在引力作用下均朝质量较大粒子的方向移动.空间中的粒子以引力的形式相互影响,使粒子群向最优解的区域展开搜索.算法中,每个粒子包括4个特征:位置、惯性质量、主动引力质量和被动引力质量,粒子的位置即为问题的解.
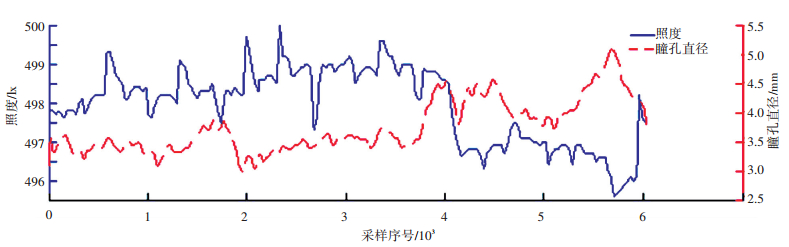
设在一个D维搜索空间中包含n个粒子,定义粒子i的位置为
|
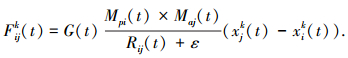
|
(2) |
式中:Mpi(t)粒子的被动吸引质量;Mat(t)为j粒子的主动吸引质量;ε为较小的常量;Raj(t)为i粒子与j粒子之间的欧氏距离;G(t)为t时刻的引力常数.
粒子i在时刻t受到的作用力Fik(t)为其他粒子对其引力之和,即
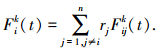
|
(3) |
式中:rj为粒子j对粒子i引力的权重,取[0, 1]的随机数;Fijk(t)为k维空间上粒子j对粒子i的引力.
粒子i在下一时刻的速度和位置的方程组为
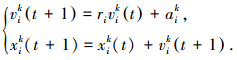
|
(4) |
t时刻粒子i在k维空间上的加速度为
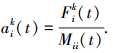
|
(5) |
式中Mii(t)为粒子i的惯性质量.
设引力质量与惯性质量相等,使用适应度函数表示粒子的质量.引力质量与惯性质量按如下方程组更新为
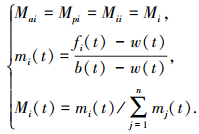
|
(6) |
式中:i=1, 2, …, n;fi(t)为t时刻粒子i的适应度值;解决最大值问题时,b(t)和w(t)按如下方程组定义为
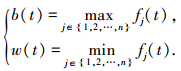
|
(7) |
GSA算法中粒子位置的更新规则是将当前每一个粒子按照万有引力定律向最优解方向移动,避免了实际应用中因更新规则和移动规律选择不当导致的收敛速度和搜索精度的降低,且粒子受到的引力Fik(t)由全局粒子的质量Maj(t)和位置Xi决定,可充分利用搜索空间全局解状态信息和适应度信息,提高搜索效果.
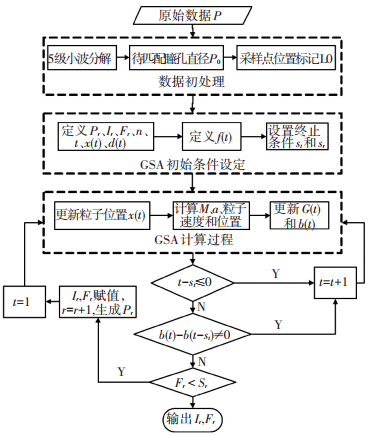
3.2 基于瞳孔直径的冲突快速识别方法本文尝试使用GSA搜索瞳孔直径超过阈值的时刻,进而识别交通冲突.本文拟在原始GSA搜索策略的基础上调整其迭代过程,提出一种可实现准确、快速识别交通冲突位置及数量的GSA-T方法.该方法的具体识别步骤如下.
1) 数据初处理.将含有交通冲突的瞳孔直径数据进行眨眼数据剔除和5级小波分解,生成待匹配瞳孔直径数据P0, 计L0为P0中每个采样点的初始序号并将其作为采样点的位置标记.
2) GSA初始条件设定.设待匹配瞳孔直径数据为Pr(r为识别结果数量,初始值为0),识别出的交通冲突时段瞳孔直径第一采样点初始序号的集合为Ir,相应适应度值为Fr,设搜索粒子数量为n,迭代次数为t(初始迭代次数为t=1),粒子位置x(t)(x(t)={x1,x2, …, xn})对应的瞳孔直径数据为d(t),以粒子位置为第中位采样点且采样点个数为Lm的瞳孔直径数据为Pxi,适应度值f(t)=d(t),GSA终止条件为适应度值连续st(st∈N*)次相同,交通冲突识别过程终止条件为适应度值小于已知冲突中最小的瞳孔直径峰值sr(sr∈R+).
3) 适应度值计算.更新粒子位置为x(t)(xi为Pr采样点初始序号范围内的随机数,i=1, 2, …, n),按照式(1)~(5)计算M、α及搜索粒子的速度和位置(维数k=1),按照式(6)更新G(t)和b(t).
4) 过程迭代. (a)若t-st≤0,则t=t+1,运行步骤4;(b)若t-st>0, b(t)-b(t-st)≠0,则t=t+1,运行步骤3;(c)若t-st>0,b(t)-b(t-st)=0且b(t)≥sr,将最优粒子位置赋值为Ir,相应适应度值b(t)赋值为Fr,r=r+1,去除Pr-1中初始序号为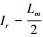
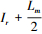
5) 结果输出.输出瞳孔直径位置Ir和对应的适应度值Fr,方法流程如图 6.
|
图 6 GSA-T识别方法流程 |
本方法在每次瞳孔直径识别中均使用GSA搜索方式寻找瞳孔直径最大值及其对应位置,从而减少了搜索次数;此外,本方法第4步(b)过程重新生成Pr的作用在搜索到目标数据段后剔除该段数据以生成新的待匹配数据并继续进行识别,从而克服了GSA仅可搜索最优值的弊端,在保证识别出所有交通冲突的前提下减少了运算量.
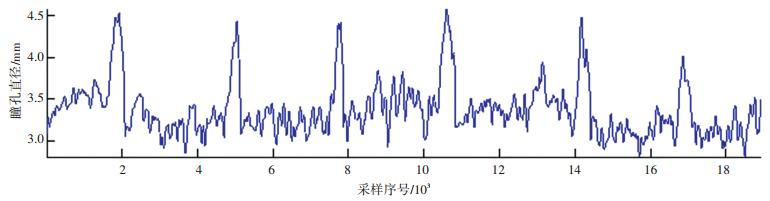
4 识别方法验证与结果分析 4.1 识别方法验证1) 数据初处理.将490 lx照度下的H1、H2、H3组试验数据作为验证数据.由于试验场景为直线路段,所以每一车速的重复试验需单独进行,因此将每一车速下多个重复试验数据合并于一组数据作为瞳孔直径识别的基础数据.
将含有撞固定物冲突的瞳孔直径数据进行眨眼数据剔除和5级小波分解,生成P0和L0.待匹配瞳孔直径曲线如图 7.
|
图 7 待匹配瞳孔直径曲线 |
2) GSA初始条件设定.设搜索粒子数量n=20,初始迭代次数为t=1,st=50,sr=4.
3) GSA计算过程.按照式(1)~(5)计算M、a及搜索粒子的速度和位置,按照式(6)更新G(t)和best(t).
4) 过程迭代. (a)若t-50≤0,则t=t+1,运行步骤4;(b)若t-50>0, b(t)-b(t-st)≠0,则t=t+1,运行步骤3;(c)若t-50>0,b(t)-b(t-st)=0且b(t)≥4,将最优粒子位置赋值为Ir,相应适应度值b(t)赋值为Fr,r=r+1,生成新的待匹配瞳孔直径数据Pr,t=1,运行步骤3;(d)若t-50>0,b(t)-b(t-st)=0且b(t) < 4,停止迭代.
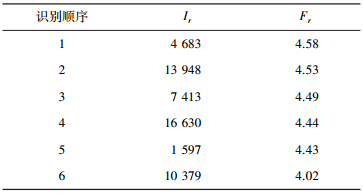
5) 结果输出.输出的瞳孔直径位置和对应的适应度值见表 3.
| 表 3 Ir与Fr的识别结果 |
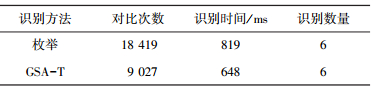
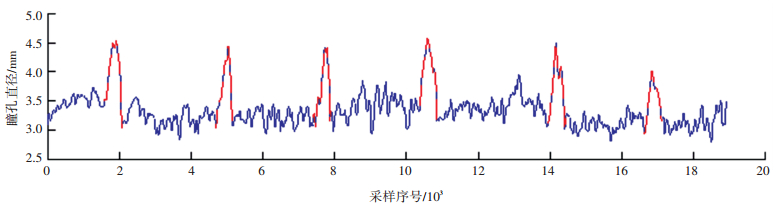
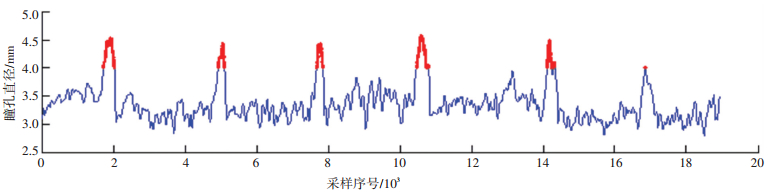
枚举法以逐点扫描的方式对待匹配数据进行计算比较,而GSA-T方法借鉴GSA搜索策略计算全局最优值,因而可避免对大量非目标数据的计算比较.此外,GSA-T方法通过剔除已识别数据并生成新的待匹配数据解决了原始GSA仅搜索全局最优解的问题,同时避免了数据的重复搜索,进而提高了算法的识别速度. GSA-T方法的识别结果曲线如图 8,其中红色虚线表示识别出的撞固定物冲突区域.枚举法对撞固定物冲突识别结果如图 9,其中红色圆圈表示识别出的撞固定物冲突点.枚举法与GSA-T方法的识别效果对照见表 4,表中GSA-T数据为30次识别所得均值,对比次数进行了四舍五入取整处理.
|
图 8 GSA-FFT方法识别结果 |
|
图 9 枚举法识别结果 |
| 表 4 识别效果对比表 |
由表 4和图 8、9可见,本实例中共有18 919个采样点,使用枚举法逐点扫描需进行18 419次瞳孔直径值的对比,相比GSA-T方法在非目标采样点处多进行了9 392次傅里叶变换,是GSA-T方法中对比计算量的2倍,由于GSA-T方法需要进行相对复杂的初始化过程和迭代循环过程,其识别时间虽不是枚举法识别时间的0.5倍,但仍比枚举法节省了170 ms.此外,枚举法与GSA-T识别方法均完成了全部撞固定物冲突下瞳孔直径的识别,两种方法在识别精度上无显著差别.但是,枚举法未能明确标记冲突过程所对应的位置,若要达到GSA-T方法的识别效果必将延长识别时间.
因此可判断,本文所述GSA-T方法可在较短时间内有效识别交通冲突下的瞳孔直径数据位置,具有较低的时间复杂度和空间复杂度,可用于交通冲突的快速辨识和道路交通安全评价.
5 结论1) 证明了冲突刺激与瞳孔直径的相关关系,明确了基于瞳孔直径数据的交通冲突识别的可行性,为交通冲突技术领域和交通安全评价领域提供了较为新颖而有效的评价指标.
2) 克服了原始GSA搜索算法仅可搜索最优解的缺陷,提出了基于瞳孔直径的GSA-T交通冲突快速识别方法,为完善不同交通冲突类型下的瞳孔直径模型,研究基于驾驶人眼动特征的交通冲突量化方法,逐步构建交通安全评价体系提供了技术支持.
3) 由于试验条件有限,仅进行了将训练场内高墙作为固定障碍物的冲突试验,造成对瞳孔直径与冲突间关系分析的局限性.在后续研究中,将进行其他交通冲突形式的试验研究,并对驾驶人瞳孔直径和试验环境进行更为准确的量化和更为深入的分析.
| [1] |
张苏. 中国交通冲突技术[M]. 成都: 西南交通出版社, 1998.
|
| [2] |
MINDERHOUD M M, BOVY P H L. Extended time-to-collision measures for road traffic safety assessment[J]. Accident Analysis & Prevention, 2001, 33(1): 89-97. |
| [3] |
ALIAKSEI L, ASE S, CHRISTER H. Evaluation of traffic safety, based on micro-level behavioural data:theoretical framework and first implementation[J]. Accident Analysis and Prevention, 2010, 42(6): 1637-1646. DOI:10.1016/j.aap.2010.03.021 |
| [4] |
孟祥海, 徐汉清, 王浩, 等. 基于TTC及DRAC的高速公路施工区追尾冲突研究[J]. 交通信息与安全, 2013, 30(6): 6-10. |
| [5] |
徐汉清. 基于碰撞时间的侧向冲突指标计算模型研究[J]. 城市道桥与防洪, 2014(6): 268-271. |
| [6] |
(苏)巴布可夫. 道路条件与交通组织[M]. 祁振庆, 译. 北京: 中国建筑工业出版社, 1983.
|
| [7] |
FU C Y, PEI Y L. Analysis on driver's physiological and eye movement characteristics under alcohol effect[J]. Advances in Intelligent Transportation System & Technology, 2012, 5(5): 138-143. |
| [8] |
NEUMANN D L, LIPP O V. Spontaneous and reflexive eye activity measures of mental workload[J]. Australian Journal of Psychology, 2002, 54(3): 174-179. DOI:10.1080/00049530412331312764 |
| [9] |
EINHÄUSER W, STOUT J, KOCH C, et al. Pupil dilation reflects perceptual selection and predicts subsequent stability in perceptual rivalry[J]. Proceedings of the National Academy of Sciences, 2008, 105(5): 1704-1709. DOI:10.1073/pnas.0707727105 |
| [10] |
STEINHAUER S R, SIEGLE G J, CONDRAY R, et al. Sympathetic and parasympathetic innervation of pupillary dilation during sustained processing[J]. International Journal of Psychophysiology, 2004, 52(1): 77-86. DOI:10.1016/j.ijpsycho.2003.12.005 |
| [11] |
WINN B, WHITAKER D, ELLIOTT D B, et al. Factors affecting light-adapted pupil size in normal human subjects[J]. Investigative Ophthalmology & Visual Science, 1994, 35(3): 1132-1137. |
| [12] |
PEDROTTI M, MIRZAEI M A, TEDESCO A, et al. Automatic stress classification with pupil diameter analysis[J]. International Journal of Human-Computer Interaction, 2014, 30(3): 220-236. DOI:10.1080/10447318.2013.848320 |
| [13] |
罗石贵, 周伟. 路段交通冲突技术研究[J]. 公路交通科技, 2001, 18(1): 65-68. |
| [14] |
罗石贵, 周伟. 路段交通冲突的调查技术[J]. 长安大学学报(自然科学版), 2003, 23(1): 71-75. |
| [15] |
RASHEDI E, NEZAMABADI-POUR H, SARYAZDI S. GSA:a gravitational search algorithm[J]. Information Sciences, 2009, 179(13): 2232-2248. DOI:10.1016/j.ins.2009.03.004 |
 2016, Vol. 48
2016, Vol. 48