2. 鲁东大学 土木工程学院, 264025 山东 烟台
2. School of Civil Engineering, Ludong Univesity, 264025 Yantai, Shandong, China
既有钢筋混凝土桥梁结构在服役过程中普遍发生钢筋锈蚀,这将引致桥梁结构承载能力下降及技术状况劣化.特别是沿海地区高氯离子含量的腐蚀环境以及冬季除冰氯盐的大量使用,使得桥梁结构中的钢筋在氯离子的侵蚀下加速锈蚀.在役的公路与铁路桥梁结构,除承受自重恒载的作用外,更主要的是承受车辆活载的反复作用,反复荷载作用损伤累积到一定程度将引发无预兆的脆性疲劳破坏.尤其是经济发展带来交通量的飞速增长及货运超载的普遍存在,使得车辆荷载对桥梁结构的疲劳作用越来越显著.毋庸置疑,钢筋混凝土桥梁结构处于氯离子腐蚀环境与车辆荷载反复作用的双重不利影响下,即混凝土中钢筋处于锈蚀与疲劳的耦合作用下,钢筋的力学性能将发生显著变化.钢筋混凝土梁内主筋的力学性能是评价混凝土桥梁结构安全性及耐久性的重要指标之一.由此可见,开展锈蚀钢筋混凝土梁疲劳后主筋力学性能变化规律的研究具有重要的理论价值与现实意义.
目前,对于混凝土中锈蚀钢筋的静力与疲劳性能的研究,在理论、试验方面积累了丰富的成果[1-4].吴庆等[5]对模拟气候环境和恒电流两种加速锈蚀方法获得的锈蚀钢筋混凝土梁中主筋进行了静力拉伸试验,建立了与锈蚀率相关的钢筋本构关系模型.曹建安等[6]与张伟平等[7-8]对替换下来旧梁内的自然锈蚀钢筋进行了轴向拉伸疲劳试验,回归拟合出了自然锈蚀钢筋的疲劳曲线方程.李士彬等[9]对通电加速锈蚀方法获取的锈蚀钢筋进行了轴向拉伸疲劳试验,研究了锈蚀钢筋的疲劳寿命退化规律. Nakamura等[10]对锈蚀钢丝的疲劳性能进行了研究.此外,国内外学者们通过锈蚀钢筋混凝土梁的疲劳加载试验,研究了锈蚀钢筋混凝土梁的弯曲疲劳性能[11-14]、疲劳作用下锈蚀钢筋与混凝土间的粘结退化机理[15],分析了主筋锈蚀率、疲劳强度与疲劳寿命之间的定量关系[16].既有的相关研究大多侧重锈蚀钢筋在未疲劳情况下的力学性能及锈蚀对钢筋的轴向拉伸疲劳寿命、钢筋混凝土梁的弯曲疲劳寿命的影响.然而,对于锈蚀疲劳后混凝土中钢筋力学性能的研究,目前开展的研究较少,尚无统一的认识.易伟建等[17]通过对疲劳加载后的锈蚀钢筋混凝土梁中钢筋进行静力拉伸试验,定性分析了钢筋力学性能随锈蚀率以及应力幅的变化规律.
本文在已有研究工作的基础上,结合既有钢筋混凝土桥梁结构的实际受力情况,进一步通过锈蚀钢筋混凝土梁的疲劳加载试验及锈蚀疲劳钢筋的静力拉伸试验,分析得出了锈蚀疲劳后混凝土中钢筋力学性能的退化规律,定量化地提出了锈蚀疲劳后混凝土中钢筋的本构关系模型,以此为在役混凝土桥梁结构中钢筋锈蚀疲劳性能的研究提供可靠的理论支撑和试验支持.
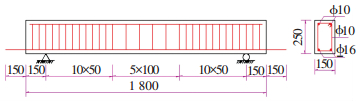
1 试验过程概述 1.1 试验梁设计与制作本次试验共设计13根钢筋混凝土梁,其中,对11根梁的主筋加速锈蚀后进行疲劳加载,1根梁进行疲劳加载但主筋未锈蚀,1根梁主筋未锈蚀且不进行疲劳加载,试验梁的截面尺寸及配筋如图 1所示.混凝土设计强度等级为C25,实测抗压强度为31.3 MPa.主筋采用同批次出厂的直径为16 mm的HRB335,实测屈服强度为478 MPa、抗拉强度为608 MPa.主筋伸出梁端15 cm,用于连接导线.绑扎钢筋前,用高精度电子天平对主筋的初始质量逐根称重.
|
图 1 试验梁截面尺寸及配筋(mm) |
试验梁成型并养护28 d后,按照文献[18]的试验方法,对主筋通直流电进行电化学加速锈蚀,如图 2所示.根据法拉第定律,通过控制施加电流的大小及通电时间,使试验梁主筋达到不同的锈蚀率.电化学加速锈蚀试验达到预期的锈蚀率之后即进行疲劳加载试验.

|
图 2 主筋通直流电加速锈蚀试验照片 |
试验梁用三分点弯曲疲劳加载,在双通道微机控制电液伺服动静态加载试验系统(JAW-500K/4)上进行,如图 3所示.加载频率采用4 Hz,控制模式为试验力控制,按正弦波形疲劳加载.经分析计算,疲劳荷载上限值取70 kN,为未疲劳加载的未锈蚀梁静力破坏荷载的47.3%,以模拟桥梁荷载在正常使用状态短期效应组合下的作用效应.疲劳荷载下限值取30 kN,相当于桥梁的恒载作用效应.与之相应的主筋疲劳应力下限值为95.1 MPa,上限值为221.9 MPa,应力幅为126.8 MPa.当试验梁内某一根主筋发生疲劳断裂,即试验力限值的变化幅度超过8%时,作动器立即卸载保护,防止破坏后的试验梁继续受力,试验终止.

|
图 3 试验梁疲劳加载试验系统 |
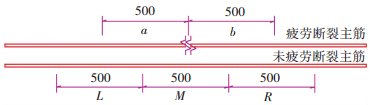
试验梁疲劳破坏后,凿碎混凝土取出锈蚀疲劳后的主筋,根据图 4截取钢筋段试样,如图 5所示.按照文献[18]中规定的锈蚀率测定方法,除锈、打磨、烘干后称重,以质量损失作为实测的钢筋段锈蚀率.之后,按照文献[19]的试验方法,在微机屏显式液压万能试验机(WEW-1000D)上进行截取钢筋段的静力拉伸试验,如图 6所示.
|
图 4 钢筋段截取位置示意图(mm) |

|
图 5 截取的部分钢筋段试样照片 |

|
图 6 钢筋静力拉伸试验装置 |
试验梁内主筋通电加速锈蚀一段时间后,可在主筋位置周围的试验梁侧面或底面的外表面观察到出现顺筋方向的锈胀裂缝(见图 7),并随着锈蚀程度的增加锈胀裂缝继续延伸发展,但锈胀裂缝不会在同一主筋位置处的梁侧面和底面的外表面同时出现.锈胀裂缝的出现使得钢筋与混凝土之间的粘结作用迅速削弱,并随着裂缝的发展粘结损伤逐渐积累.

|
图 7 试验梁局部锈胀裂缝照片 |
在疲劳循环加载到一定次数后,所有锈蚀后的试验梁内的某一根主筋突然疲劳断裂,发生脆性的疲劳破坏(见图 8),其具体表现为在疲劳破坏时可清晰听到钢筋断裂的声音,试验力的变化幅度突然超限,试验梁跨中挠度突然增大,在主筋疲劳断裂处形成突然增宽的主裂缝,无任何预兆,具有突然破坏的危险性.未锈蚀的试验梁在循环加载200万次之后不发生疲劳破坏.

|
图 8 试验梁疲劳破坏照片 |
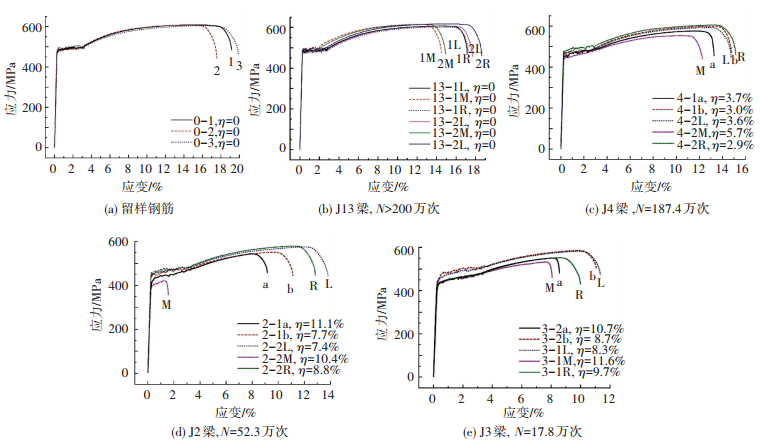
在三分点弯曲疲劳加载的情形下,主筋各区段的应力幅不等,加载点间1/3纯弯区段应力幅最高且保持不变,加载点至支点间1/3弯剪区段应力幅由最大值线性递减至零.对各钢筋段进行静力拉伸试验得到的应力-应变曲线如图 9所示.其中,曲线编号采用“A-BC”的形式,其中A代表试验梁编号,B代表钢筋编号,C代表钢筋试样的截取位置,例如4-1a表示试验梁编号为4、钢筋编号为1、钢筋截取位置为a.
|
图 9 试验梁内钢筋应力-应变曲线 |
图 9(b)为未锈蚀梁内主筋在疲劳循环加载200万次后的应力-应变关系曲线,可以看出,有明显的屈服台阶,表现出较好的延性特征,仅仅是随着疲劳应力幅的增加屈服台阶的长度稍有变短,极限拉应变有所变小.对比图 9(a)、9(b)可以发现,在钢筋不发生锈蚀的情况下,疲劳作用对未锈蚀钢筋的力学性能(强度、延性)没有明显影响.
由图 9(c)~9(e)可以看出,梁内主筋锈蚀疲劳之后的应力-应变曲线表现出以下明显的特征:1)屈服强度降低;2)极限拉应变减小;3)屈服台阶的特征发生转变, 即屈服段与强化段渐渐融合,屈服时的应力值由未锈蚀钢筋的在某一值附近往复波动变为波动增加.钢筋锈蚀疲劳以后,其材料特性已经逐步发生了转变,即由最初的软钢转化为出现了一定程度的硬化,变化程度的大小与锈蚀疲劳的程度有关,即与锈蚀率的大小、疲劳循环次数的多少、疲劳应力幅的大小有关.
由图 9(b)~9(e)可以看出,对于不同试验梁中的钢筋,随着锈蚀率的增大,梁中钢筋极限拉应变与屈服强度都相应减小,锈蚀率越大减少的幅度越明显.对于同一片试验梁中的钢筋,在疲劳次数相同的情况下,梁中钢筋极限拉应变随疲劳应力幅的增大而有所减小.在较高锈蚀率及疲劳应力幅的影响下,钢筋的屈服台阶渐不明显,软钢的特性发生了较大程度的硬化.
图 9(d)中M段钢筋在屈服阶段就发生了突然的拉断破坏,这是因为在锈蚀疲劳作用下钢筋中产生了疲劳裂纹,如图 10所示.疲劳裂纹的出现是疲劳破坏的前兆,是锈蚀疲劳损伤最直接的表现形式.从试验得到的应力-应变曲线图中可以发现,疲劳裂纹的出现导致钢筋的屈服强度大幅降低,延性几乎完全丧失,破坏时表现出无预兆的脆断,疲劳损伤的累积已进入末期,突然破坏的可能性增加.未发生疲劳破坏之前,疲劳裂纹的出现不但使得随着疲劳作用次数的继续增多,将产生无预兆的疲劳破坏,而且承载能力极限状态的破坏形态也随之发生改变,在极低的延伸率下即突然拉断破坏,不再出现延性破坏特征,具有突然性和危险性.

|
图 10 锈蚀疲劳钢筋中产生的疲劳裂纹 |
锈蚀疲劳后钢筋的力学性能发生改变,其本构关系也相应随之改变.本文在文献[20]提出的未锈蚀未疲劳加载的原状钢筋本构模型的基础上,结合锈蚀疲劳钢筋的应力-应变曲线特征,提出如下的锈蚀疲劳后混凝土中钢筋的本构关系模型,如图 11所示.

|
图 11 锈蚀疲劳钢筋本构关系模型 |
当0≤ε≤εy时,
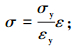
|
(1) |
当εy<ε≤εh时,
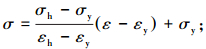
|
(2) |
当εh < ε≤εu时,
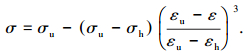
|
(3) |
式中:σy、εy分别为锈蚀疲劳钢筋弹性变形阶段与屈服阶段转折点的应力、应变值;σh、εh分别为锈蚀疲劳钢筋屈服阶段与塑性硬化阶段转折点的应力、应变值;σu、εu分别为锈蚀疲劳钢筋塑性硬化阶段与缩颈变形阶段转折点的应力、应变值.
根据本试验60根锈蚀疲劳后试验梁内钢筋的应力-应变曲线中360个特征点的实测数据值,回归拟合得到σy、εy、σh、εh、σu、εu与原状钢筋应力-应变曲线特征点、锈蚀率、疲劳循环次数之间的定量关系模型为
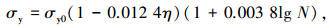
|
(4) |
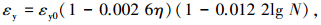
|
(5) |
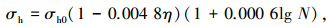
|
(6) |
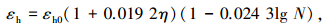
|
(7) |
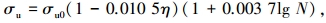
|
(8) |
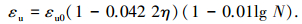
|
(9) |
式中:σy0、εy0分别为原状钢筋弹性变形阶段与屈服阶段转折点的应力、应变值;σh0、εh0分别为原状钢筋屈服阶段与塑性硬化阶段转折点的应力、应变值;σu0、εu0分别为原状钢筋塑性硬化阶段与缩颈变形阶段转折点的应力、应变值;η为锈蚀率,本次试验中钢筋试样锈蚀率的范围为0%~14.6%;N为疲劳循环次数,本次试验中最大循环次数为200×104.
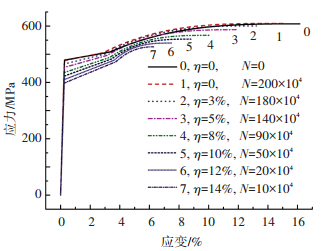
针对上述得到的锈蚀疲劳钢筋的本构关系定量模型,代入不同的锈蚀率及循环次数,便可绘制出不同锈蚀疲劳程度下钢筋的本构关系曲线族,如图 12所示.从图 12可以发现,在既有钢筋混凝土梁桥实际荷载水平下,钢筋的弹性模量不因锈蚀疲劳的影响而发生变化.锈蚀率为5%、循环次数为140万次的钢筋,其屈服强度、极限拉应变分别比原状钢筋减少了5.4%、25.9%.当钢筋的锈蚀率达到14%、循环次数仅为10万次时,其屈服强度、极限拉应变分别比原状钢筋减少了17.0%、61.1%.同时屈服台阶的特征也发生了明显的变化,由平直线变为斜直线,屈服段与强化段逐渐融合.在锈蚀与疲劳的耦合作用下,钢筋的本构关系发生了显著变化.
|
图 12 不同锈蚀疲劳程度下钢筋本构关系曲线族 |
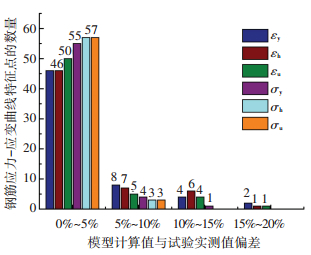
对于本次试验中锈蚀疲劳后的钢筋,本文提出的本构关系定量模型中特征点的计算值与实测值的偏差分析的统计结果如图 13所示.从图中可以看出,模型计算值与试验实测值的偏差,εy、εh、εu绝大多数为0%~10%,σy、σh、σu绝大多数为0%~5%,对于工程应用而言,其准确程度是令人满意的.上述分析计算结果检验了所拟合出的模型特征点计算公式的可靠性,证明了本文提出的本构关系定量模型具有一定的适用性,可为长期活载作用下锈蚀钢筋混凝土桥梁结构的计算与评估提供借鉴.
|
图 13 本构关系模型偏差分布 |
1) 疲劳循环加载200万次后,未锈蚀钢筋与原状钢筋一样,表现出较好的延性破坏特征,表明疲劳作用对未锈蚀钢筋的力学性能(强度、延性)没有实质影响.
2) 钢筋锈蚀疲劳后应力-应变曲线的特征发生了明显的改变, 即屈服强度降低、极限拉应变减小、屈服台阶特征转变,材料特性由软钢转化为表现出一定程度的硬化特征,变化程度的大小与锈蚀疲劳的程度有关.
3) 疲劳裂纹的出现使得钢筋在极低的延伸率下即突然拉断破坏,屈服强度显著降低,延性几乎完全丧失,具有脆性破坏的危险性.
4) 锈蚀疲劳后钢筋的本构关系随之发生改变,定量化地提出了锈蚀疲劳后混凝土中钢筋的本构关系模型,可用于锈蚀钢筋混凝土桥梁结构在长期车辆活载作用下的计算与评估.
| [1] |
赵羽习. 钢筋锈蚀引起混凝土结构锈裂综述[J]. 东南大学学报(自然科学版), 2013, 43(5): 1122-1134. DOI:10.3969/j.issn.1001-0505.2013.05.035 |
| [2] |
MALUMBELA G, ALEXANDER M, MOYO P. Steel corrosion on RC structures under sustained service loads:a critical review[J]. Engineering Structures, 2009, 31(11): 2518-2525. DOI:10.1016/j.engstruct.2009.07.016 |
| [3] |
ALIAKSEI L, ASE S, CHRISTER H. Evaluation of traffic safety, based on micro-level behavioural data:theoretical framework and first implementation[J]. Accident Analysis and Prevention, 2010, 42(6): 1637-46. DOI:10.1016/j.aap.2010.03.021 |
| [4] |
郭冬梅, 项贻强, 程坤, 等. 沿海在役钢筋混凝土桥梁的钢筋锈蚀模型[J]. 哈尔滨工业大学学报, 2012, 44(12): 100-104. DOI:10.11918/j.issn.0367-6234.2012.12.018 |
| [5] |
吴庆, 袁迎曙. 锈蚀钢筋力学性能退化规律试验研究[J]. 土木工程学报, 2008, 41(12): 42-47. DOI:10.3321/j.issn:1000-131X.2008.12.007 |
| [6] |
曹建安, 文雨松. 锈蚀钢筋的疲劳试验研究[J]. 长沙铁道学院学报, 1998, 16(4): 15-18. |
| [7] |
FU C Y, PEI Y L. Analysis on driver's physiological and eye movement characteristics under alcohol effect[J]. Advances in Intelligent Transportation System & Technology, 2012, 5(5): 138-143. |
| [8] |
ZHANG W P, SONG X B, GU X L, et al. Tensile and fatigue behavior of corroded rebars[J]. Construction and Building Materials, 2012, 34(1): 409-417. |
| [9] |
李士彬, 张伟平, 顾祥林, 等. 加速锈蚀钢筋的疲劳试验研究[J]. 铁道学报, 2010, 32(5): 93-97. |
| [10] |
NAKAMURA S, SUZUMURA K. Experimental study on fatigue strength of corroded bridge wires[J]. Journal of Bridge Engineering, 2012, 18(3): 200-209. |
| [11] |
王海超. 钢筋混凝土构件腐蚀疲劳试验研究与理论分析[D]. 大连: 大连理工大学, 2004.
|
| [12] |
YI W J, KUNNATH S K, SUN X D, et al. Fatigue behavior of reinforced concrete beams with corroded steel reinforcement[J]. ACI Structural Journal, 2010, 107(5): 526-533. |
| [13] |
FANGC Q, YANG S, ZHANG Z. Bending characteristics of corroded reinforced concrete beam under repeated loading[J]. Structural Engineering and Mechanics, 2013, 47(6): 773-790. DOI:10.12989/sem.2013.47.6.773 |
| [14] |
OYADO M, HASEGAWA M, SATO T. Characteristics of fatigue and evaluation of RC beam damaged by accelerated corrosion[J]. Quarterly Report of RTRI, 2003, 44(2): 72-77. DOI:10.2219/rtriqr.44.72 |
| [15] |
AL-HAMMOUD R, SOUDKI K, TOPPER T H. Bond analysis of corroded reinforced concrete beams under monotonic and fatigue loads[J]. Cement and Concrete Composites, 2010, 32(3): 194-203. DOI:10.1016/j.cemconcomp.2009.12.001 |
| [16] |
吴瑾, 王晨霞, 徐贾, 等. 疲劳荷载下锈蚀钢筋混凝土梁弯曲性能试验研究[J]. 土木工程学报, 2012, 45(10): 118-124. |
| [17] |
易伟建, 孙晓东. 锈蚀钢筋混凝土梁疲劳性能试验研究[J]. 土木工程学报, 2007, 40(3): 6-10. |
| [18] |
普通混凝土长期性能和耐久性能试验方法标准: GB/T 50082-2009[S]. 北京: 中国建筑工业出版社, 2009.
|
| [19] |
金属材料拉伸试验第1部分: 室温试验方法: GB/T 228. 1-2010[S]. 北京: 中国标准出版社, 2011.
|
| [20] |
PARK R, PAULAY T. Reinforced concrete structures[M]. New York: John Wiley & Sons, 1975.
|
 2016, Vol. 48
2016, Vol. 48


