2. 常州市建设工程结构与材料性能研究重点实验室(常州工学院), 213002 江苏 常州
2. Changzhou Key Lab of Structure Engineering and Material Properties(Changzhou Institute of Technology), 213002 Changzhou, Jiangsu, China
GFRP(glass fiber reinforced plastics, GFRP)沥青混合料是一种新型桥面结构形式,与传统混凝土桥面系相比,具有自重轻,抗疲劳性能好、耐化学腐蚀性好、施工方便等优点. GFRP沥青混合料是GFRP板与沥青混合料粘结而成的结合材料,在结合界面附近往往存在缺陷,会导致结合强度下降,而且由于界面的存在而引发应力集中并产生残余应力等,使界面附近的材料处于较高的应力水平,所以由结合材料结构的强度往往都取决于界面的强度[1-2].结合材料具有界面端应力奇异性和界面裂纹裂尖的非r-0.5振荡应力奇异性[3-5],界面本身与母材的强度也不同,传统的强度评价方法,如以应力为基本评价参数的材料力学的方法,和以均质材料裂纹应力强度因子为基本评价参数的断裂力学的方法,都不能用来评价结合材料的强度或断裂行为,需要建立一套针对界面性能的评价方法,为结合材料的强度提供必要的理论基础.本文利用双材料巴西盘试件进行GFRP沥青混合料试验研究,它可以通过改变加载角度模拟试件的各种破坏模态,便于实现结合材料试件强度的全面研究.
1 界面裂纹描述Williams[1]最早采用特征函数法研究了各项同性弹性材料界面裂纹尖端附近的应力场和位移场的振荡奇异性,指出界面裂尖前沿应力场特征值为一对共轭复根
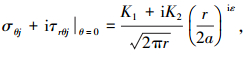
|
(1) |
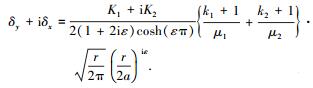
|
(2) |
式中:ε为振荡因子,β为Dundurs参数[5],Ei为弹性模量,νi为泊松比,μi为剪切模量,ki为材料参数, K1/K2为应力强度因子SIF(stress intensity factor).
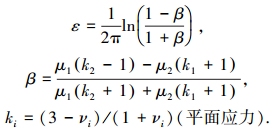
|
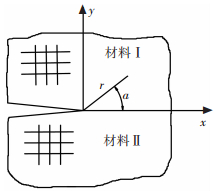
Suo[6]进一步分析了各向异性材料结合材料的界面问题.对于图 1所示正交各向异性材料界面裂纹,当材料主轴方向与界面一致时,裂尖前沿应力场和开口位移场的形式为
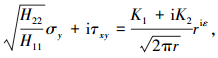
|
(3) |
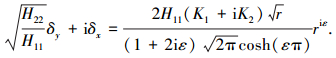
|
(4) |
|
图 1 裂尖界面裂纹 |
式中Hij为汉密尔顿矩阵的分量为
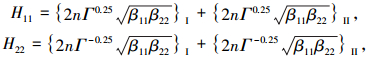
|

|
将式(3)、(4)复变函数形式展开,整理得到K1、K2,应力法:
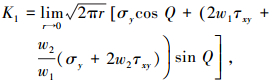
|
(5) |

|
(6) |
式中
位移法:
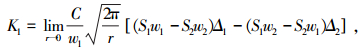
|
(7) |
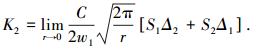
|
(8) |
式中:
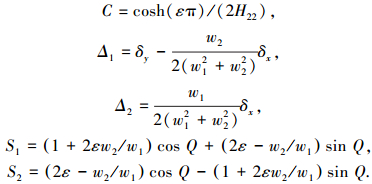
|
当材料由正交各向异性材料退化为各项同性的结合材料时,2W1=1,W2=0,即可得到各项同性均质材料K1/K2.
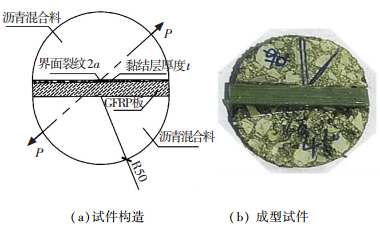
2 GFRP沥青混合料巴西盘试验 2.1 试验描述试件由两个沥青混合料半圆、GFRP板条粘结而成,如图 2(a).试件制作时,首先将沥青混合料半圆、GFRP板条固定在专用夹具上,然后注入环氧树脂胶,放入标准养护室养护不少于48 h方可试验.界面裂纹在试件制作过程中预制,在一侧沥青混合料半圆粘帖薄膜,确保注胶时胶水不能进入薄膜和沥青混合料空腔,待试件养护硬化后割掉沥青混合料侧面薄膜,形成界面预制裂纹.试件制作时,为了防止在界面端及无预制裂纹界面破坏,对这些部位进行了加强,如图 2(b).
|
图 2 巴西盘试件 |
沥青混合料为AC-16F环氧树脂改性沥青混凝土,通过沥青混合料弯曲试验测得AC-16F环氧树脂改性沥青混凝土在室温下弹性模量为173 MPa,抗拉极限强度为1.32 MPa,泊松比为0.297. GFRP板条采用E玻璃纤维和乙烯基树脂制成,其中纤维增强材料采用了无碱纱(1200Tex)、0/90和-45/45双轴布(双向比例为1:1),基体为乙烯基树脂.板厚度为10 mm,共有4层纱层,5层纤维布层,均沿纵向铺设,对称铺层,各铺层厚度分别为:纱层2.0 mm,双轴纤维布层0.4 mm,GFRP材料弹性常数见表 1.
| 表 1 GFRP材料弹性常数(x/y) |
试件参数:沥青混合料半圆半径r=50 mm,厚度b=10 mm;粘结层厚度t=2 mm;GFRP板条长度、宽度、厚度分别为100、10、10 mm;预制界面裂纹长度2a=10 mm.
巴西盘试件利用SDS10KN试验机加载,试件夹持采用混凝土专用夹具,如图 3所示.位移模式加载,加载速度为1 mm/min.加载角β分别在25°、30°、40°、45°、50°、60°、70°、80°、90°时,加载角β为加载力P与界面层夹角.

|
图 3 试件加载 |
当试件出现下列情况之一时即认为破坏,停止试验并记录破坏荷载:1)试件界面可见裂纹;2)试件界面剥离;3)界面端出现裂纹或破坏;4)其他部位开裂.
2.2 试验结果描述进行了3组巴西盘试验,每组9个试件,共27个试件. 21个试件界面裂纹破坏,两个在夹持端附近沥青混合料开裂,3个界面端开裂,1个因粗骨料附近缺陷开裂.
发生界面裂纹破坏的21个试件破坏形式分为两类:1)沿界面剪开破坏.裂纹首先自界面裂尖(左裂尖或右裂尖)开始扩展,随着荷载的施加,裂纹扩展迅速,很快发生界面剪开破坏,这类破坏发生在加载角度β为25°~45°的试件,如图 4(a)所示;2)裂纹向沥青混合料曲折破坏和界面拉开破坏.裂纹扩展始于界面裂尖(左裂尖或右裂尖),随着荷载的施加,裂纹以斜线的形式向沥青混合料(母材弱侧)扩展,裂纹扩展较第一种类型破坏缓慢,直至裂纹贯通沥青混合料半圆,导致巴西盘破坏,这类破坏发生在加载角度β为50°~90°的试件,如图 4(b)、4(c)所示,其中图 4(b)中斜线为裂纹扩展路径,图 4(c)中界面上微小突起为界面拉开破坏时,遗留着界面上的沥青混合料小块.裂纹在沥青混合料中扩展时,由于粗骨料的存在,可能会影响裂纹扩展路径.

|
图 4 试件典型破坏形式 |
剔除6个无效试件数据,21个有效试件数据取相同试件的破坏荷载平均值作为最终试件破坏荷载值,试件在加载角度β为25°、30°、40°、45°、50°、60°、70°、80°、90°时,对应的破坏荷载P分别为1 972、1 793、2 256.7、1 501、1 270.2、1 502.1、1 648.9、1 910.7、1 802 N.
3 有限元分析 3.1 有限元模型有限元分析的目的是将GFRP沥青混合料巴西盘试验荷破坏荷载P施加到巴西盘有限元模型,通过有限元计算的界面裂尖附近的奇异位移场数据,利用数值计算反推出界面裂尖奇异场的断裂力学参数[7-9]界面应力强度因子SIF K1/K2,进行GFRP沥青混合料巴西盘强度评价.
GFRP沥青混合料巴西盘有限元模型如图 5所示,两个沥青混合料半圆和环氧树脂粘结层采用shell63单元;GFRP条为正交异性材料,采用层单元shell199单元模拟,有限元模型中GFRP板材料与铺层参数见表 1. GFRP板条与沥青混合料非预制裂纹界面区域采用接触单元targe169和conta171模拟;沥青混合料半圆与GFRP之间预制界面裂纹区域网格加密,沥青混合料半圆与粘结层预制裂纹之间的界面自由,单元划分3级控制,中央界面区域网格加密,预制界面裂纹裂尖附近进一步细化,裂尖附近单元最小网格尺寸0.25 mm,有限元模型共6 005个节点,5 918个单元.

|
图 5 巴西盘试件有限元模型 |
绝大多数结合材料的界面裂纹的应力强度因子没有解析解,也没有类似于断裂力学的1/4奇异单元可用,只能通过数值计算求取[10].本文参考断裂力学常用的数值外插法[11],利用界面裂纹尖端后缘的有限元张开位移计算界面SIF[12-13].应力强度因子K为裂纹尖端出对应于r=0时的值,然而直接的数值计算无法达到r=0,因此采用外插法来计算K.在有限元计算中,界面裂纹尖端后缘的裂纹张开位移值δxi、δyi和那个对应的坐标值r可以直接获得.对应于每一个ri>0,都有一组非奇异的位移值δxi、δyi及Ki.
构造函数(ri,KⅠi),利用最小二乘法原则,以函数数据点和设定曲线之间的方差小为目标进行拟合.假定ri、KⅠi满足线性关系,则有

|
(9) |
当r=0时,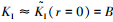
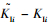
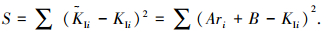
|
(10) |
根据最小二乘法原则,须满足

|
(11) |
得

|
(12) |
因此B值即为所求界面SIF K1/K2.
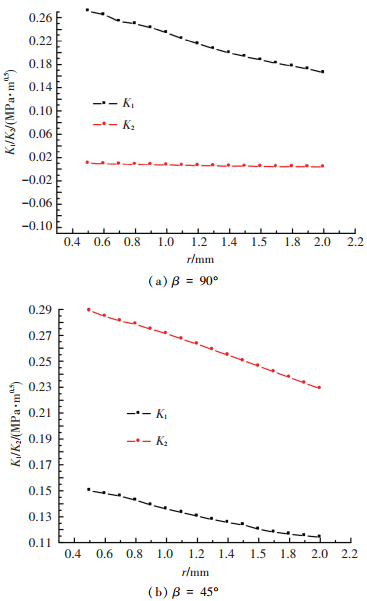
3.3 试验结果分析图 6表示加载角度β=90°巴西盘试件界面SIF K1/K2与到界面裂尖距离r关系,外加荷载P90为加载角度β=90°时巴西盘试件对应的试验破坏值.
|
图 6 界面SIF K1/K2 |
图 6可以看出,界面SIF K1/K2与到界面裂尖距离r表现出良好的线形,这说明式(9)假定是合理的,由式(12)可以计算得到两个加载工况下的界面SIF K1/K2:加载角β=90 °时界面SIF数值K1=0.303 MPa·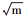
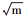
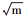
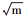
从图 6可以看出,当加载角度β=90°,即Ⅰ型模态下,界面SIF K2也不等于0,这是由于模态Ⅰ、Ⅱ型界面SIF K1/K2不仅仅与单独的δxi或δyi有关,而是同时与δxi、δyi均有关,所以界面SIF K1/K2与均质材料裂纹KⅠ/KⅡ有本质区别(为了区别于均质材料,界面应力强度因子记为K1/K2). SIF K2=0.012 MPa·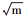
加载角度β分别为25°、30°、40°、45°、50°、60°、70°、80°、90°加载工况下, 巴西盘试件界面SIF K1/K2数值计算结果汇总如表 2所示.
| 表 2 不同加载工况下界面SIF K1/K2数值计算结果 |
表 2表明,当加载角由25°到90°变化时,界面SIF K1逐渐增大,K2逐渐减小.当加载角β=90°时,K1=0.303,K2=0.012,K2/K1=4.0%,即界面裂尖奇异位移场支配区以δy为主,但δx也起作用;当加载角β=25°时,K1=0.056,K2=0.388,K1/K2=14.4%,即界面裂尖奇异位移场支配区以δx为主,δy也起作用.
当加载角在25°~45°之间时,巴西盘试件界面SIF K2远大于K1,即位于这个加载角度范围的巴西盘试件,试件破坏模态由K2控制,断裂首先自界面裂尖处起裂,沿着界面扩展,直至界面完全剪开,这与试件试验现象完全一致,如图 4(a)所示.试件所用的粘结胶脆性很大,所以整个裂纹扩展和破坏过程试件很短.
随着加载角由50°~80°增大,巴西盘试件界面SIF K1逐渐增大、K2逐渐减小,两者数值相当,此时加载的巴西盘试件断裂模态由复合应力强度因子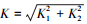

当加载角度达到80°~90°时,巴西盘试件界面SIF K1在试件破坏模态中起主导作用,此时巴西盘试件裂纹依然自界面裂尖处起裂,向母材弱侧沥青混合料作微小曲折,然后随着荷载的增大沥青混合料被拉断,沥青混合料的断口近似平行于界面.在加载角度80°~90°有效试件为5个,加载角度80°试件3个,加载角度90°试件2个. 2个90°试件是沥青混合料沿着界面被拉断,断裂近似为一条直线,而且断口上能分辨出界面裂纹起裂向沥青混合料扩展的痕迹,如图 4(c)所示. 3个80°试件中,2个试件断口为斜线,1个试件断口为直线,可能的原因是80°时SIF K1大于K2,但两者的差值还没达到K1起主导作用的程度,加上试验误差,使得加载角度为80°的3个试件破坏断口出现了分化.
将表 2的数值计算结果以模态角γ=arctan(K2/K1)和断裂破坏时的复合应力强度因子K之间的关系图来表示,如图 7所示.可以看出,在不同模态角下试件断裂破坏时的临界复合应力强度因子Kic是不同的,所以在进行GFRP沥青混合料界面强度评价时不能单单以Ki≥Kic作为破坏准则,还需要考虑Kic对应的模态角.

|
图 7 各种模态下界面裂纹复合应力强度因子 |
界面复合应力强度因子Ki达到临界复合应力强度因子Kic时,界面裂纹将开始扩展,可能的扩展路径有沿界面、向沥青混合料一侧曲折和向GFRP板一侧曲折3个方向,决定界面裂纹实际起裂的参数是模态角γ.当界面裂纹有向较强材料GFRP一侧曲折趋势时,先达到界面破坏条件,此时GFRP还未达到破坏条件,发生界面破坏.当界面有向较弱材料沥青混合料一侧曲折趋势时,如果模态角较小,则会先达到沥青混合料曲折破坏条件,发生曲折破坏;如果模态角较大,则会先达到界面破坏条件,发生界面破坏.以加载角25°试件为例,界面复合应力强度因子Ki达到临界复合应力强度因子Kic时,对应的模态角γ=81.8°,发生界面破坏.
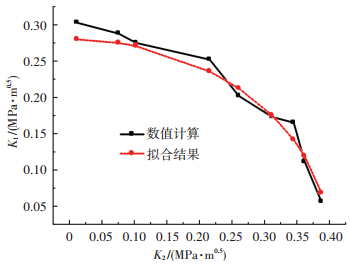
根据表 2所列K1/K2数值计算结果,整理成图 8的形式,并对数据进行拟合.可以看出GFRP沥青混合料巴西盘试件断裂破坏时应力强度因子表现为椭圆分布形式.拟合椭圆强度曲线的长轴、短轴分别记为K2c*、K1c*,即界面的断裂韧性.
|
图 8 界面破坏的椭圆强度准则 |
K1c*表示GFRP沥青混合料抵抗界面拉开的能力,K2c*表示GFRP沥青混合料抵抗界面剪切的能力.在图 8的椭圆强度拟合曲线中K2c*=0.398,K1c*=0.263,K2c*>K1c*,表明GFRP沥青混合料抵抗界面剪切的能力强于抵抗界面拉开的能力,即GFRP沥青混合料发生界面拉开破坏的可能大于界面剪切破坏.
4 结论1) 采用含预制界面裂纹的双材料巴西盘进行了GFRP沥青混合料的断裂力学性能分析,讨论了不同加载角度下界面预制裂纹试件的破坏规律.含预制界面裂纹的双材料巴西盘试验能很好地反映GFRP沥青混合料在拉伸、拉剪等不同荷载作用下的断裂过程和破坏形式.
2) 加载角度在25°~45°的巴西盘试件,试件破坏模态由K2控制,发生界面剪开断裂;加载角度在50°~80°时,巴西盘试件断裂模态由复合应力强度因子K控制,发生界面曲折破坏,断裂裂纹扩展路径表现为斜线,沥青混合料被拉断;加载角度在80°~90°时,试件破坏模态由K1控制,发生界面拉开破坏,沥青混合料的断口近似平行于界面. GFRP沥青混合料应力强度因子K1/K2表现为椭圆分布,符合椭圆强度准则.
3) 利用界面裂尖后缘裂纹张开位移外插计算的界面SIF K1/K2,计算方法简单实用,可以作为GFRP沥青混合料界面强度的评价参数.
| [1] |
WILLIAMS M L. The stresses around a fault or a crack in dissimilar media[J]. Bull Seismol Soc Am, 1959, 49(2): 199-204. |
| [2] |
RICE J R, SIH G C. Plane problems of cracks in dissimilar media[J]. App Mech, 1965, 32: 418-423. DOI:10.1115/1.3625816 |
| [3] |
ERDOGAN F. Fracture problems in composite materials[J]. Eng Fract Mech, 1972, 4: 811-840. DOI:10.1016/0013-7944(72)90018-5 |
| [4] |
COMNINOU M. Interface crack with friction in the contact zone[J]. J Appl Mech Trans ASME, 1977, 44: 780-786. DOI:10.1115/1.3424179 |
| [5] |
DUNDERS J. Effect of elastic constants on stress in a composite under plane deformation[J]. Composite Materials, 1967, 1: 310-322. DOI:10.1177/002199836700100306 |
| [6] |
SUO Z G. Singularities, interface and cracks in dissimilar anisotropic media[J]. Proc Roy Soc, 1990, A427: 331-358. |
| [7] |
XU J Q, YUUKI R. Stress intensity factors for interface cracks between dissimilar orthotropic materials[J]. Trans of JSME, 1994, 60(577): 1943-1950. DOI:10.1299/kikaia.60.1943 |
| [8] |
LEE G H, CUI C B, BEOM H G. Edge delamination in an orthotropic bimaterial consisting of a thin film and a substrate[J]. Acta Mech, 2014, 225: 2583-2594. DOI:10.1007/s00707-013-1084-y |
| [9] |
MANKOUR A, BACHIR B B, BELHOUARI M. Brazilian disk test simulation intended for the study of interfacial cracks in bi-materials[J]. Computational Materials Science, 2012, 43: 696-699. |
| [10] |
LEVESQUE G, ARAKERE N K, MECHOLSKY J, et al. Numerical and experimental investigation of mixed-mode fracture parameters on silicon nitride using the Brazilian disc test[J]. Fatigue & Fracture of Engineering, 2013, 33(8): 490-503. |
| [11] |
解德, 钱勤, 李长安. 断裂力学中的数值计算方法及工程应用[M]. 北京: 中国科学出版社, 2009: 7-15.
|
| [12] |
ZHONG Zhipeng, REN Dalong, WAN Shui. A new numerical method for determining collapse load-carrying capacity of structure made of elasto-plastic material[J]. Journal of Central South University of Technology, 2014, 21(1): 398-404. DOI:10.1007/s11771-014-1953-0 |
| [13] |
钟志鹏, 万水, 任大龙. 巴西圆盘中心裂纹摩擦接触问题的逐点Lagrange乘子法[J]. 东南大学报(自然科学版), 2012, 42(5): 994-999. |
 2016, Vol. 48
2016, Vol. 48