2. 扬州大学 建筑科学与工程学院, 225009 江苏 扬州;
3. 宁波大学 海运学院, 315211 浙江 宁波
2. College of Civil Science and Engineering, Yangzhou University, 225009 Yangzhou, Jiangsu, China;
3. Maritime College, Ningbo University, 315211 Ningbo, Zhejiang, China
对于我国城市道路常见的四幅路断面类型,路外停车右转驶入对主路车流的影响主要表现为停放车辆在到达出入口前的变道、减速、等待等行为使主路各车道车流速度发生变化,从而产生一定长度的影响区,形成瓶颈路段导致上游道路的拥堵.因此,如何基于停放车辆的驶入特征,定量化分析其对主路车流的影响特性,对于进一步分析主路车流的速度变化、影响区长度的演变规律及如何在出入口处实施科学的交通组织具有一定的现实意义.
目前国内外主要针对公交停靠站点与路内停车带等对路段交通流的影响[1-3]进行了研究,且主要是以道路的全幅或半幅断面为分析对象,模型反映的是所研究断面的平均车流状态.如张卫华[4]、王涛[5]分别研究了公交车与社会车辆在路段混合行驶及分道行驶条件下的速度-流量关系模型,葛宏伟[6]研究了不同类型公交站点车辆停靠对道路交通流影响的理论模型,梅振宇[7]和贺晓琴[8]分别研究了路内停车带对路段车流速度和延误的影响,而停车驶入的阻滞干扰效应在国内交通流研究中,尚未有专门的深入研究.
停放车辆在驶入停车场的过程中,不同的变道距离、驶入时间等对主路各车道车辆的干扰程度各不相同,如果仅仅将道路的全幅或半幅作为研究对象,并不能完全准确反映出所有车道车流的微观变化,对于停车驶入过程的影响分析也将不尽全面.对于四幅路单向各车道而言,无论停放车辆以何种方式驶入,都将会经过最右侧车道,因此要想全面分析停车驶入对主路各车道车流的影响,就必须首先以最右车道为对象开展研究,这是进一步分析其他车道车流影响特性的基础与关键,具有重要的现实意义.
1 数据采集 1.1 调查地点的选取在选取观测地点时,遵循以下几个原则:1)出入口的位置应能保证车辆在到达其影响区域前已到达正常的行驶速度;2)出入口的位置与上下游公交站点和相邻出入口应确保足够长距离;3)主路的线形应尽量顺直,纵坡无大的起伏,且路面平整;4)停车场出入口的周边范围应便于仪器架设与观测;5)停车场接入主路的机动车流量在高峰与平峰时段变化明显.
1.2 出入口影响区间的确定选取南京市中山南路的路外停车场出入口进行了预调查,研究表明停放车辆驶入时,从减速、停靠到驶出机动车道,一般要5~8 s,机非隔离带开口中心线上游0~20 m处车流的平均车速为35 km/h,上游20~40 m处车流的平均车速为50 km/h;绝大数停放车辆在距离开口中心线20 m范围内开始减速,且在减速前已完成变道.停放车辆驶入过程中,在距离出入口上游40~70 m的区间内,车流的平均车速数值波动较大.因此,为了各种驶入形式调查数据标准的统一,便于利用建立的影响模型来评价不同驶入方式对交通流的影响程度,对出入口上游80 m内开展调查,即调查A点与机非隔离带开口中心线B点距离取值为80 m.如图 1所示.

|
图 1 调查区域示意图 |
根据出入口选址的原则,本文选取南京市中山南路商贸大厦停车场为观测地点,其接入道路为四幅路双向六车道.选择在天气良好、交通和道路状况均正常的时间进行调查,选取高峰时段兼顾平峰时段,具体为上午8:00—11:00时,下午16:00—19:00时.
2 停车驶入前的主路车流基本模型 2.1 建模思路停车场接入路段主路上游的机动车辆在行驶到出入口附近区域时将会受到心理因素、道路条件、交通条件各种影响因素的干扰,其车流特性将会与无出入口路段存在一定的差异性,很难用独立变量加以简单描述.因此,本文基于实测数据来建立路阻函数模型.主要步骤:1)分析主路最右侧车道的速度分布特性及相互之间的关联性;2)选取各种交通阻抗因素,并将其抽象为相应的模型变量,通过对交通流特性的分析,剔除影响较弱的变量;3)对其他变量采用相关分析的方法,选取显著性大与相关性强的因素作为模型变量;4)对于车道宽度、车道位置等非交通性的影响因素,选取相应的畅行车速与各车道实际通行能力作为基本参数.
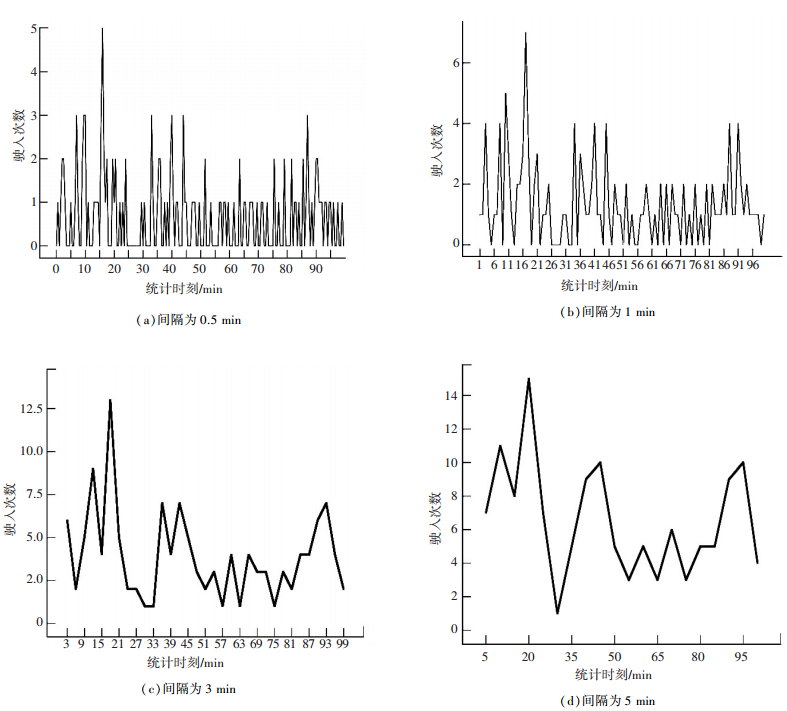
2.2 统计时间间隔国内许多学者在研究交通流模型时,大多数选择了5 min为统计时间间隔,但是本文研究的是停放车辆驶入前后路段最右侧车道交通流的变化,如果以3 min或5 min作为统计时间间隔,则车流在短时间内的变化容易被均一化,不能反应出实际的变化特征.本文通过实测数分别绘制了以0.5、1、3、5 min为统计间隔下驶入次数曲线,如图 2所示.通过比较发现,0.5 min和1 min最能体现停放车辆的短时内驶入频率,3 min和5 min统计的次数波动较大;相关研究成果[9]表明绝大部分车辆可以在30 s内完成驶入过程,而路段交通流消散时间一般在45 s左右,若采用3 min和5 min时,主路机动车的速度等指标易被平均化,由于停放车辆的驶入过程所造成的影响难易被准确捕捉.相比之下,选择0.5 min和1 min的时间间隔,更易描述短时内机动车与非机动车交通流的阻滞和冲突的变化.因此,本文选取1 min作为统计路外停车影响指标和机动车与非机动车流指标的时间间隔.
|
图 2 不同统计间隔下驶入次数随时间变化曲线 |
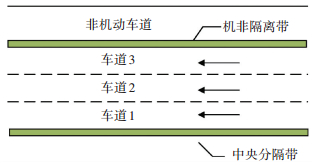
为了便于统一研究,本文确定了车道编号规则,即最靠近主路中心线的车道为车道1,依次向非机动车道方向编号分别为车道2、3,因此最右侧车道即为车道3,图 3为四幅路的车道编号示意.
|
图 3 四幅路各车道编号示意 |
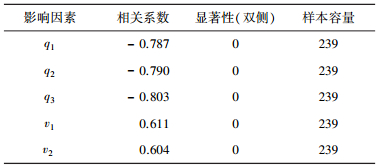
简单分析可知,车道3速度的影响因素可能有车道1流量q1、车道2流量q2、车道3流量q3、车道1速度v1和车道2速度v2.因此基于实测数据,进行相关性分析,结果见表 1.可以看出v3与其他变量的相关统计双尾检验相伴概率小于0.01,能够通过临界值为0.05的相关检验,说明所有的变量都与v3显著相关.但是,对于多元回归而言,每个自变量与因变量简单相关性包含着其他自变量对因变量的作用,在一些情况下无法较为真实准确的反映事物之间的相关关系[10].
| 表 1 车道3的速度与各影响因素的相关性 |
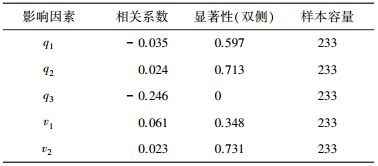
运用SPSS分析软件来计算各变量与各车道交通流速度之间的偏相关系数,结果见表 2.
| 表 2 车道3的交通流速度与各影响因素的偏相关性 |
从表 2中可以看出,v3与q3的偏相关系数为-0.246,统计双尾检验相伴概率为0, 小于0.01,能通过临界值为0.05的相关检验,其余影响因素也均不能通过检验,主要原因是控制变量之间存在相关性,如分析v3与q2的偏相关时,控制变量q3与v1之间相关性大,而在分析v3与q2的Pearson相关时,则包括了q2、q3、v2、v1的正效应,因此进行偏相关分析剔除它们的影响后,两者之间的显著性变小.
因此,分析可知车道3车辆的平均车速v3的影响因素仅有q3可以通过检验,其他均不能通过检验,其显著性影响因素仅为q3.所以,对于四幅路而言各车道的平均车速只与本车道的流量密切相关,而与其他车道的流量与速度相关性很小.
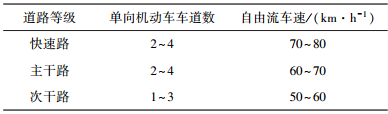
2.4 各车道实际通行能力和畅行车速的确定黄艳君[11]通过研究给出了城市道路不同等级的自由流速度推荐值,见表 3.本文所研究的对象均为城市主干路且单向车道数为3车道,且各车道实际观测车速最大值均小于60 km/h,与研究结论比较吻合.因此综合考虑畅行速度取值均为60 km/h.
| 表 3 不同道路等级的自由流车速推荐值 |
文献[12]规定,城市道路在设计车速为60 km/h时一条车道的基本通行能力(小客车单位)为1 800 pcu/h,则对于路段的单个车道,其实际通行能力为
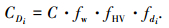
|
(1) |
式中:CDi为车道i的实际通行能力,pcu/h;C为车道的基本通行能力,pcu/h;fw为车道宽度影响修正系数,当车道宽度为3.5 m时取值为1.0;fHV为交通流中有非小客车时,交通组成对通行能力的修正系数,取值建议为0.85~0.95;fdi为车道i利用系数.
本文以双向6车道的四幅路为研究对象,通过实测分析出入口影响区各车道的流量分布比例可知,对于单向3车道的四幅路,车道1、2、3的流量分布比例为36.9:45.6:17.5.假设车道2的利用系数为1,则可计算出其余各车道的利用系数,即车道1、2、3的各车道利用系数为0.809:1:0.384.根据式(1),计算出四幅路道路断面类型下车道3的实际通行能力CDi,其中fw取值为1.0,fHV取值为0.9,fdi取值为0.384,则实际通行能力CDi为622 pcu/h,畅行车速v0标定值为60 km/h.
2.5 基本模型的建立以(BPR)路阻函数模型为基础,建立停车驶入前车道3的路阻函数模型,其模型为
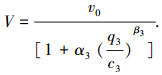
|
(2) |
利用实测的数据标定式(2),结果为α3=1.909,β3=0.418.将参数代入(2),则模型为

|
(3) |
经回归方程的F检验:相关系数为0.773,F统计值为74.58,均可以通过显著性水平5%下的检验.
3 停车驶入后对路段交通流的影响模型 3.1 影响因素分析1) 停放车辆的驶入频率λ.停放车辆驶入频率指在统计时间间隔内停放车辆到达的次数,由停放车辆的特性分析[13]可知,车辆的到达服从泊松分布,其到达具有一定的随机性,且在单位时间内平均发生的事件数通常用λ表示.
2) 停放车辆驶入影响时间t.驶入影响时间t指停放车辆在机动车道减速、等待及完全驶离机动车道的过程中,当驶入时间过长时对主路上游社会车辆的干扰时间,取值[14]为
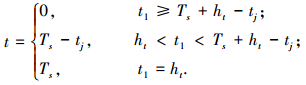
|
(4) |
式中:Ts为停放车辆经历从机动车道减速至机非隔离带开口处、停车等待、非机动车出现可接受的群间隙、车头开始进入非机动车道、车尾驶离机动车道的过程中所耗费的总时间,s;ht为车流的平均车头时距,s;tj为停放车辆以初始速度v1在减速距离内行驶的时间,s.
由调查数据分析可知,在统计时间间隔内停放车辆会有多次的驶入,而且每次驶入的时间也各不相同,对上游车流的影响时间也会不一样,其计算公式为

|
(5) |
式中:ti为第i次停车驶入影响时间,s;λ为停放车辆的驶入频率,辆/min.
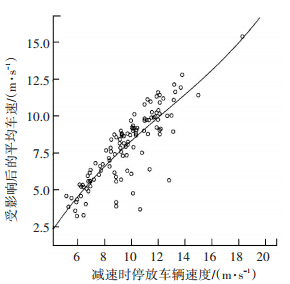
3) 停放车辆开始减速时的初始速度vJ.当停放车辆驶入后,上游社会车辆受到其干扰导致速度减小,呈现出一定的变化规律,图 4为二者的散点关系图.当拟合曲线采用三次方时,R2=0.724拟合度较好,说明二者相关性较强.
|
图 4 停放车辆减速时的速度与上游车流平均速度关系 |
4) 停放车辆开始减速时地点与停车场出入口中心线的距离s.由调查分析可知,当减速距离过短时,减速度就比较大,此时就会造成上游车辆车速的显著变化,不利于行车的安全.在统计时间间隔内,若有λ次车辆驶入,则有λ个减速距离,计算平均减速距离为
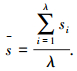
|
(6) |
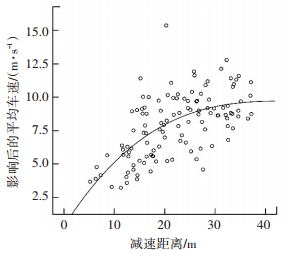
图 5为平均减速距离与速度的散点图,拟合曲线为三次方时,R2=0.391拟合度较好,说明二者具有一定的相关性.
|
图 5 停放车辆的平均减速距离与车流平均速度的散点图 |
拟通过回归分析的方法建立受停车影响后的速度模型,因变量为影响后的社会车辆平均速度,自变量为各个影响因素,建立多元回归方程为
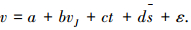
|
(7) |
式中:v为停车驶入影响后的社会车辆平均速度,m/s;vJ为停放车辆开始减速时的初始速度,m/s;t为停车驶入影响时间,s;s为停放车辆开始减速时与停车场出入口的平均距离,m.
将实测数据代入模型,利用SPSS分析软件进行处理后,相关分析,得出多元回归模型的复相关系数R=0.983,判断系数R2=0.967,调整判定系数为0.966,估计的标准差为0.441 819 3.
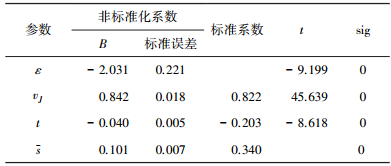
表 4为模型回归系数列表,常数项a=-2.031,b=0.842,c=-0.040,d=0.101,经T检验,b、c、d的概率ρ值均为0.000,按给定的显著性水平0.05的情形下,均有显著性意义.因此,影响模型为

|
(8) |
| 表 4 模型回归系数分析 |
又由式(3)可知,车道3的车辆在无影响时的平均车速为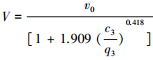
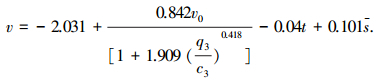
|
(9) |
利用所建立的影响模型进一步分析各影响变量对社会车辆速度影响的敏感性.
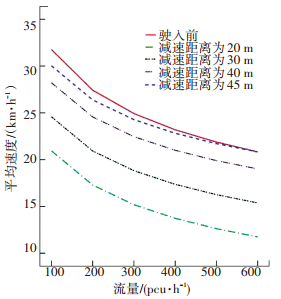
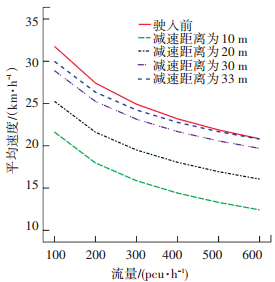
4.1 减速距离对速度的影响分析图 6、7分别为停车驶入影响时间为40、10 s,无停放车辆驶入与停车车辆在不同减速距离下驶入时,主路最右侧车道社会车辆的平均车速的对比分析.
|
图 6 驶入影响时间在40 s时的速度 |
|
图 7 驶入影响时间在10 s时的速度 |
从图中可以看出:1)在相同的减速距离下,车辆平均速度均随流量的增大呈现下降的趋势,同时速度与流量的变化趋势总体上可以分为3个阶段.第1阶段, 100 pcu/h < q < 200 pcu/h, 即饱和度0.16 < v/c < 0.32,此时流量与速度之间变化的幅度最大;第2阶段, 200 pcu/h < q < 400 pcu/h, 即饱和度0.32 < v/c < 0.64,此时流量与速度之间变化的幅度相对第1阶段有所减小;第3阶段, q>400 pcu/h, 即饱和度v/c>0.64, 此时流量与速度之间变化的幅度最小.这说明当0.16 < v/c < 0.32时,社会车辆受到停放车辆减速距离影响的敏感度较高. 2)在相同的流量下,停放车辆的减速距离越短,则对社会车辆的平均车速影响越大.如图 6中,当流量为400 pcu/h时,减速距离为20 m时,影响后的速度为13.72 km/h,而当减速距离为40 m时,影响后的速度为21.00 km/h. 3)随着停放车辆驶入影响时间的减小,其对社会车辆无影响的减速距离阈值也在减小.如图 6、7中所示,当驶入影响时间为40 s,减速距离阈值在45 m左右对社会车辆的影响最小;而当驶入影响时间为10 s时,此时对社会车辆影响最小的减速距离阈值则减小为33 m左右.
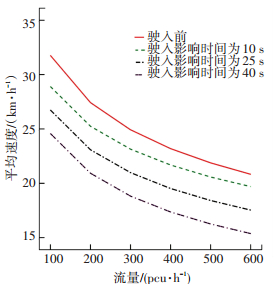
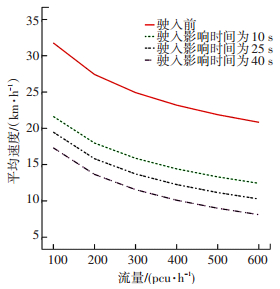
4.2 停车驶入影响时间对速度的影响分析图 8、9分别为停车驶入假设减速距离分别为30、10 m,无停放车辆驶入与停车车辆在不同驶入影响时间下,主路最右侧车道社会车辆平均车速的对比分析.从图中可以看出:1)相同的驶入影响时间下,车辆平均速度均随流量的增大呈现下降的趋势. 图 8、9可以发现当流量在100~550 pcu/h时,速度的变化幅度均较大,说明在此流量区间范围内,社会车辆对于停放车辆的影响时间敏感度较高.当流量大于600 pcu/h后,速度的变化幅度则相对变小,主要是因为此时车流的饱和度较大,社会车辆整体平均速度都比较低. 2)在相同的流量下,停放车辆的驶入影响时间越短,则对社会车辆的平均车速影响越小.如图 9中,当流量为400 pcu/h时,减速影响时间为10 s时,影响后的速度为14.40 km/h,而当减速影响时间为40 s时,影响后的速度为10.10 km/h. 3)随着停放车辆驶入减速距离的减小,在相同的减速影响时间下其对社会车辆影响程度在增大.如图 8、9中所示,当车辆的减速影响时间为10 s时,当驶入减速距离为30 m时,停放车辆驶入造成度变化幅度为1.53%,而当驶入减速距离为10 m时,速度变化幅度则增大为31.65%.
|
图 8 减速距离为30 m时的速度 |
|
图 9 减速距离为10 m时的速度 |
1) 当无停车驶入时,最右侧车道的车流速度仅与本车道流量密切相关,且该车道的利用系数仅为0.384.
2) 当有停车驶入时,最右侧车道的车流速度与停放车辆的驶入频率、驶入影响时间、减速距离及本车道的流量等参数密切相关.
3) 当有停车驶入影响时,停放车辆的减速距离与受其影响后社会车辆的平均车速呈现反比关系.当减速距离20 m≤s≤30 m时,影响后的速度变化幅度为23.91%,当减速距离40 m≤s≤30 m时,影响后的速度变化幅度为23.53%,当减速距离40 m≤s≤45 m时,影响后的速度变化幅度为9.52%.
4) 当有停车驶入影响时,停放车辆的驶入影响时间与受其影响后社会车辆的平均车速呈现正比关系.当影响时间10 s≤t≤25 s时,影响后的速度变化幅度为12.5%, 当影响时间25 s≤t≤40 s时,影响后的速度变化幅度为13.9%,当影响时间t>40 s时,影响后的速度变化幅度为20.2%.
5) 当减速距离小于10 m时,社会车辆的车速受停车驶入影响幅度较大.如当车辆的减速影响时间为10 s时,当驶入减速距离为30 m时,停放车辆驶入造成速度变化幅度为1.53%,而当驶入减速距离为10 m时,速度变化幅度则增大为31.65%.
| [1] |
JASON C. Roadway capacity related to curb parking maneuver[J]. Journal of the transportation Engineering Division, 1973, 99(3): 467-481. |
| [2] |
JILLAR. Effects of bicycle lanes on traffic flow joint highway research project JHRP-74-10[R]. Indiana: Purdue University School of Civil Engineering West Lafayettc, 1974.
|
| [3] |
WEBSTER L. Traffic delay on urban arterial streets as a result of curb parking maneuvers[R]. Washington DC: National Research Council, 1969.
|
| [4] |
张卫华. 城市公共交通优先通行技术及评价方法研究[D]. 南京: 东南大学, 2004.
|
| [5] |
王涛. 城市道路公交车与社会车辆速度运行特性研究[D]. 南京: 东南大学, 2010.
|
| [6] |
葛宏伟. 城市公交站点停靠影响分析及优化技术研究[D]. 南京: 东南大学, 2006.
|
| [7] |
梅振宇. 城市路内停车设施设置优化方法研究[D]. 南京: 东南大学, 2006.
|
| [8] |
贺晓琴. 信号交叉口附近路边停车带的优化设置研究[D]. 南京: 东南大学, 2007.
|
| [9] |
闫星辰. 路外停车场车辆出入对城市三幅路交通影响研究[D]. 南京: 东南大学, 2012.
|
| [10] |
AKCELIK R, CHUNG E. Calibration of the bunched exponential distribution of arrival headways[J]. Road and Transport Research, 1994, 3(1): 42-59. |
| [11] |
黄艳君. 城市公共交通路段优先通行技术及评价方法研究[D]. 南京: 东南大学, 2003.
|
| [12] |
城市道路工程设计规范: CJJ37-2012[S]. 北京: 中国建筑工业出版社, 2012.
|
| [13] |
叶晓飞. 路内停车对非机动车动态交通影响机理及设置优化方法[D]. 南京: 东南大学, 2013.
|
| [14] |
邓社军, 叶晓飞, 陈峻. 路外停车场入口处车辆右转驶入过程对于主路车流影响的动态长度模型[J]. 公路交通科技, 2014, 31(3): 125-132. |
 2016, Vol. 48
2016, Vol. 48