2. 东南大学 交通学院, 210096 南京;
3. 哈尔滨工业大学 交通科学与工程学院, 150090 哈尔滨
2. School of Transportation, Southeast University, 210096 Nanjing, China;
3. School of Transportation Science and Engineering, Harbin Institute of Technology, 150090 Harbin, China
路内停车通过合理利用道路的闲散资源,一定程度上缓解了停车难的问题[1],但由于其利用道路空间资源作为停车载体,必然会对道路上机动车、非机动车、行人等交通流产生干扰[2-4],首要的干扰对象是非机动车交通系统,主要表现在:1)路内停车占用道路资源,降低了通行能力,迫使非机动车流速度变缓形成紊乱的行驶状态,甚至会诱发交通拥堵. 2)停放车辆的驶入和驶出会阻断非机动车交通流,迫使非机动车流速度迅速降低;同时与非机动车流之间发生合流、交织、分流等交通冲突,增加了安全隐患.可见,路内停车使作为交通系统中弱势群体的非机动车交通运行状态紊乱不堪,降低了非机动车交通的通行效率和安全性.因此,如何解析路内停车对非机动车流的影响规律,进而寻求合理的停车带设置方法,具有重要的意义.
关于路内停车对动态交通的影响研究,指出不间断的单向路内停车可使机动车流速度降低20%或更多[5];文献[6]研究了设置路内停车对机动车流以及机非混合交通流的影响;从速度、延误、通行能力、服务水平等角度解析了路内停车与机动车流之间作用关系[6-8].然而,在路内停车对非机动车道上纯非机动车流运行状态影响定量化研究基本处于空白,也正是本文研究重点内容.
1 基于风险持续期模型的行程时间模型将非机动车流行程时间比拟为生存分析中持续期.区间行程时间即为非机动车在路段区间行驶状态的持续,存在明显的持续期过程:起始时刻-持续时间-结束时刻[9].当路内停车对非机动车产生影响时,其行程时间的分布规律受到影响,表明行程时间持续期受到路内停车的影响.
令T为非负连续随机变量,表示非机动车通过观测路段的行程时间,S(t)为T的生存函数,f(t)为T的概率密度函数,F(t)为T的分布函数,h(t)为T的风险函数.非机动车行驶t时间后无法结束行程的概率,即样本个体的行程时间或“生存时间”大于时间t的概率,称之为T的生存函数,计算公式为
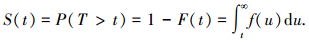
|
(1) |
式中F(t)为非机动车通过观测区间的行程时间T的分布函数,即
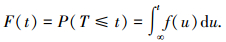
|
(2) |
非机动车通过观测区间的行程时间T的概率密度函数为
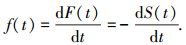
|
(3) |
风险函数h(t),用于描述被观测对象个体在某一时间点存活的条件下,在未来的单位时间里的死亡概率,即
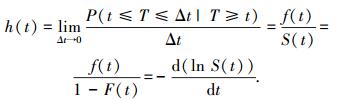
|
(4) |
因此h(t)Δt表示非机动车行程时间持续过程在时间段[t, t+Δt]结束的条件概率. h(t)在非机动车的整个行程至少持续了t时间的条件下,在下一个较短时间间隔Δt内结束的行程的瞬时概率.将影响行程时间的重要因素定义为协变量,用X表示协变量组成的向量.持续期模型引入协变量,则T的分布特征描述函数变为h(t|X)、S(t|X)、F(t|X)、f(t|X),计算方法不变,关系式为
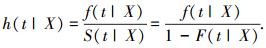
|
(5) |
Cox模型是当协变量以乘积形式exp(βX)作用于风险函数g(t|X),是一种半参数比例风险持续期模型,具有不指定基准风险函数h0(t)的分布形式、数学形式以及计算值等优点[10].为精确分析各因素对行程时间的影响,采用Cox模型,即当生存时间是连续分布且不同变量对应的风险函数之比不随着t的变化而变化时,Cox模型的比例风险函数为
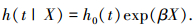
|
(6) |
式中:h0(t)为基准风险函数,表示无任何外部影响时的风险率;β为对应协变量的参数向量;X为协变量组成的向量.
对应的生存函数S(t|X)为
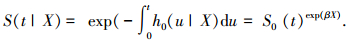
|
(7) |
式中S0(t)为t时刻的基准生存函数,表示无间接影响因素时行程时间大于t的概率.
由于Cox模型假定协变量X与时间t相互作用为0,路内停车影响都体现在g(t|X)或g(v|X)对风险函数作用上,作用效果取决于协变量的参数β不取决于变量本身,那么对时间t进行等价变量代换并不影响分析和判断协变量的作用效果.因此,用等价的速度变量代替行程时间变量,则得出区间平均车速的Cox模型,比例风险函数和对应的生存函数分别表示为
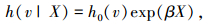
|
(8) |
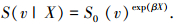
|
(9) |
采用偏最大似然参数估计方法来估计协变量X的系数β[11-12],则偏似然函数为
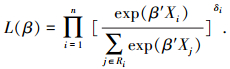
|
(10) |
式中Ri为行程时间ti的风险集,即行程时间至少为t(i)的样本集合,写成{j:tj≥ti}.然后对似然函数L(β)最大化即可得到变量X的系数β的估计值.
基准生存函数估计值表达式为
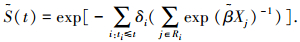
|
(11) |
模型拟合优度采用似然比法进行检验.以LL(0)表示初始的即所有回归参数为0时模型的最大似然函数值,LL(βc)表示K个回归参数在收敛时的最大似然函数值,则LR定义为
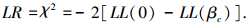
|
(12) |
LR服从K个自由度的卡方分布,由此检验估计模型对观测数据拟合的显著水平.
3 基于Cox模型的区间平均车速模型估计结果与分析 3.1 协变量选取在选择路内停车相关变量作为构建模型的潜在要素时,通过分析非机动车流速度变缓的摩擦效应和阻滞效应,主要考虑以下几个方面:1)非机动车车道有效宽度We(m),是车道实际宽度减去停车带宽度再减去两侧横向净空(共0.5 m).车道宽度对道路交通流参数的影响是最明显和最直接的因素.降低非机动车车道有效宽度是路内停车在道路条件方面最直接的影响. 2)驶入事件数Cen(次).停放车辆驶入泊位时逐渐减速直至停驶,迫使非机动车跟驰行驶,阻断交通流,显著影响了非机动车运行状态,是路内停车影响的直接表现.将驶入事件数作为协变量引入模型. 3)驶出事件数Cex(次).停放车辆驶离泊位时中速度逐渐增加,但受道路和交通条件限制,跟驰于非机动车流,无法加速至最佳行驶状态,对非机动车流产生阻滞影响,将驶出事件数作为协变量引入模型. 4)持续效应Cswe(次).由于驶入和驶出事件发生随机性和不确定性,事件的持续时间易超出统计时间间隔,事件持续影响到下一统计间隔,将其定义为持续效应变量,表征驶入和驶出事件的持续影响效应. 5)时间障碍率RT.将车辆驶入或驶离泊位的阻滞时间作为因素,定义时间障碍率加以衡量阻滞时间.时间障碍率是指统计时间间隔内总影响时间占统计间隔时间的百分比,计算公式为RT=T/TI,其中TI为统计时间间隔,T为驶入和驶出事件的总影响时间,T=n1t1+n2t2,其中n1、n2分别为单位统计间隔内停放车辆驶入和驶出次数,t1、t2为车辆驶入和驶出泊位对相邻车道车流的阻滞影响时间. 6)非机动车流量q(辆/min).流量是影响非机动车速度的重要因素,引入到模型中.非机动车流由自行车和电动自行车组成,二者的速度特性存在显著差异,导致二者受路内停车的影响存在差异.因此,建模时分别考虑二者的流量,并引入自行车和电动自行车占总流量的比例记为qcb/q和qeb/q,表征不同交通方式在模型中效用.此外,路内停车对非机动车流影响中,还存在上下客/货和并排停放事件数两个因素.但是,实际调查两类事件数极少,不满足建模样本量要求,予以剔出.
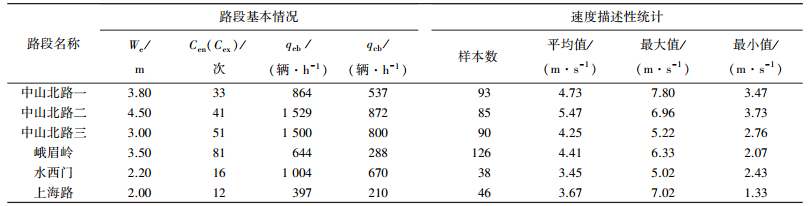
3.2 数据调查与采集选取南京市中山北路两侧、峨眉岭、水西门、上海路等三幅路路段为调查对象,选择了16:00—19:00时间段进行调查,覆盖交通流和路内车辆停放的平峰和高峰时段,基本情况如表 1所示,获取有效样本478个,每个路段代表了典型道路条件下路内停车对非机动车交通特性影响,有助于研究不同道路宽度缩减程度对非机动车流的影响.同时,由于每个路段周边土地利用的差异,各个路段的停车需求以及停车周转情况亦不相同,有益于全面采集参数与参数之间每个水平的配对数据.
| 表 1 调查路段基本参数 |
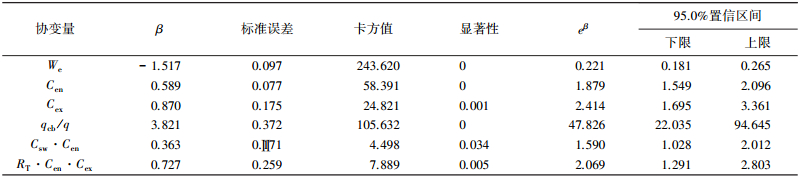
利用偏最大似然参数估计方法标定系数β,采用Wald向前选择法对十个协变量进行选择,得出模型Ⅰ标定结果如表 2所示,纳入模型的变量为有效宽度We、驶入事件数Cen、驶出事件数Cex、持续效应Cswe、自行车所占比例qcb/q,模型估计的最大似然值3 986.980,5个协变量的回归系数及模型统计显著性(Sig.)均小于0.05,表明模型具有统计学意义.但是,模型Ⅰ并未考虑协变量之间交互作用,即一个协变量与风险函数的联系依赖于另一个协变量的取值.如速度与非机动车流量之间的联系依赖于各交通方式所占比例;速度与流量/有效宽度的散点图表明速度与流量之间的联系依赖于有效宽度.
| 表 2 模型Ⅰ参数估计结果 |
因此,在模型Ⅱ引入交互作用项:持续效应与驶入、驶出事件数;时间障碍率与驶入、驶出事件数;非机动车流量与自行车、电动自行车所占比例.模型Ⅱ标定结果如表 3,与模型Ⅰ相比增加了交互项:Csw·Cen和RT·Cen·Cex,剔除了持续效应独立协变量,表明协变量之间的交互作用项是存在的.
| 表 3 模型Ⅱ参数估计结果 |
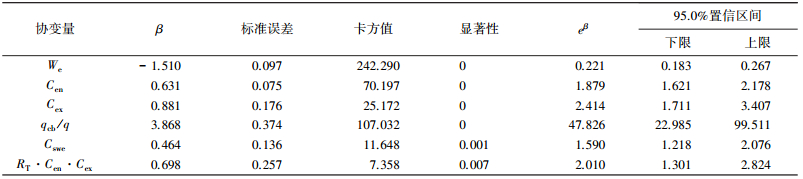
然而,Csw·Cenn仅代表了持续效应与因变量的联系依赖于驶入事件,而Cswe·Cex交互作用项并未进入模型当中,这与持续效应协变量Cswe的定义不相符合,因此,综合模型Ⅰ和Ⅱ分析结果,模型应引入独立的协变量Cswe和交互项RT·Cen·Cex,由此得出模型Ⅲ,其参数标定结果如表 4所示.
| 表 4 模型Ⅲ参数估计结果 |
模型Ⅲ的最大似然值3 978.565,LR检验值为347.823,该检验值在各种合理的显著水平上均大于6个自由度的卡方分布值,由此可知模型Ⅲ具有良好的全局拟合优度,能够较好地描述路内停车影响下非机动车速度分布.模型的回归系数的标准误差都很小,6个协变量的回归系数及模型统计显著性均小于0.01,表明模型的协变量估计结果具有较理想的显著水平,模型具有统计学意义,表明纳入模型中的协变量对区间平均速度分布具有显著影响.
模型结果表明,有效宽度We对速度降低的风险率有负效应影响,表明该变量取值增大会对区间平均速度分布有积极影响,会减少区间平均速度降低的概率.相反,其余协变量驶入事件数Cen、驶出事件数Cex、持续效应Cswe、自行车所占比例qcb/q、时间障碍率交互项RT·Cen·Cex对速度降低的风险率有正效应影响,表明该变量取值增大会对增大速度降低的风险意味着区间平均速度的降低.比较各β绝对值的大小可知,自行车所占比例qcb/q和有效宽度We对持续期长短的作用较大.
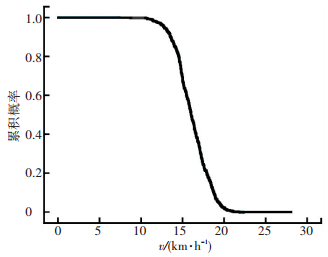
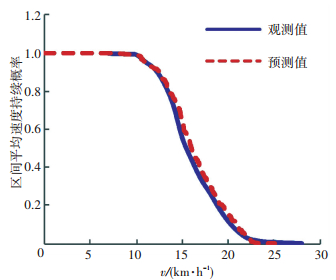
如图 1所示,持续概率估计结果成单点递减分布,随着速度的增大,持续概率逐渐减小.区间平均速度中位数为15.98 km/h,表明有一半样本通过观测路段区间的速度小于15.98 km/h;25%分位数为14.31 km/h,表明有25%的样本在观测区间中行驶过程速度小于14.31 km/h.如图 2所示,区间平均速度持续概率模型估计值与实测值的两条曲线具有类似的分布趋势,说明模型预测较为准确.
|
图 1 基于各协变量均值时生存函数曲线 |
|
图 2 区间平均速度概率模型估计值与实测值 |
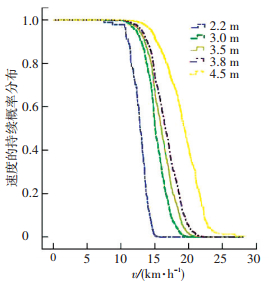
如图 3所示,4.5 m宽度条件下的速度持续期分布情况最好,3、3.5、3.8 m明显要差一些,2.2 m最差.随着车道有效宽度的增加,相同速度的持续比例越大,速度降低的风险减小. RR值结果表明,以2.2 m为基准,3、3.5、3.8 m和4.5 m的速度下降风险都要比2.2 m的低得多,指数每上升一分,速度降低风险下降分别为以前的0.138、0.085、0.063倍和0.019倍.其原因是有效宽度越小,非机动车流受停放车辆的影响更显著,发生侧向偏移的可能性更高;同时压缩了车流横向间距,降低了骑行速度.当有效宽度由4.5 m减小至3.8、3.5、3.0、2.2 m时,速度的25%分位数值分别为18.24、14.68、14.23、14.14、11.38 km/h,意味着通过观测路段的大部分样本(占总样本的75%)的平均速度分别降低了19.5%、22.0%、22.5%、37.5%.有效宽度从4.5 m减小到3.0 m的过程,速度降低幅度较小;但减小到2.2 m时,速度降低幅度非常大,其变化趋势与模型估计结果基本一致.可见,路内停车的设置要为非机动车运行保留足够车道宽度.
|
图 3 非机动车车道不同有效宽度下速度持续概率分布 |
1) 停车带设置和车辆停放过程的相关因素包括非机动车车道有效宽度、驶入和驶出事件及时间障碍率,显著影响了非机动车流的运行状态.
2) 驶入和驶出事件数、自行车所占比例和时间障碍率对非机动车流速度具有负效应影响.
3) 非机动车道有效宽度对非机动车流速度具有正效应影响,随着有效宽度的增加,速度降低的风险减小;为非机动车运行保留足够宽度,是设置路内停车要考虑的重要因素.
| [1] |
陈峻, 周志勇, 梅振宇, 等. 城市停车设施规划方法与信息诱导技术[M]. 南京: 东南大学出版社, 2007: 54-57.
|
| [2] |
BOX P C. Curb parking problems:overview[J]. Journal of Transportation Engineering, 2004, 130(1): 1-5. DOI:10.1061/(ASCE)0733-947X(2004)130:1(1) |
| [3] |
FABIEN P. Curb parking:theory and model[M]. Berkeley: Institute of Transportation Studies University of California, 1978.
|
| [4] |
YOUSIF S, PURNAWAN S. On-street parking:effects on traffic congestion[J]. Traffic Engineering Control, 1999, 40(9): 424-427. |
| [5] |
陈峻. 城市停车设施规划方法研究[D]. 南京: 东南大学, 2000.
|
| [6] |
梅振宇. 城市路边停车设施设置优化方法研究[D]. 南京: 东南大学, 2006.
|
| [7] |
张露. 路边停车对交通流影响的研究[D]. 北京: 中国农业大学, 2005.
|
| [8] |
陈峻, 贺晓琴. 信号交又口影响区路边停车的交通流延误模型[J]. 哈尔滨工业大学学报, 2009, 41(5): 130-135. |
| [9] |
PEREZ R I, TARKO A P. Calibration of capacity parameters for signalized intersections in Indiana[C]//The 84th Annual Meeting of the Transportation Research Board. Washington DC: National Research Council, 2005: 1102-1109.
|
| [10] |
COX D R. Regression models and life tables[J]. Journal of the Royal Statistical Society:Series B, 1972, 34(2): 187-220. |
| [11] |
CHANGH L, YEH T H. Exploratory analysis of motorcycle holding time heterogeneity using a split-population duration model[J]. Transportation Research Part A, 2007, 41(6): 587-596. |
| [12] |
BHAT C R. A hazard-based duration model of shopping activity with nonparametric baseline specification and nonparametric control for unobserved heterogeneity[J]. Transportation Research Part B, 1996, 30(3): 189-207. DOI:10.1016/0191-2615(95)00029-1 |
 2016, Vol. 48
2016, Vol. 48