利用X-ray CT技术,获取沥青混合料内部结构组成,分析体积参数,进而完成沥青混合料的计算机辅助设计的研究已成为沥青路面技术领域的关注热点.张肖宁[1]针对目前应用数字图像处理技术研究沥青混合料现状以及以后的发展趋势,提出了完整的技术路线.该技术路线指出,最终的目标是实现设计沥青混合料的计算机辅助设计技术.其中,沥青混合料虚拟力学是实现这一目标的关键.
利用X-ray CT技术进行沥青混合料虚拟力学试验在二维建模方面取得了相应的研究成果.虞将苗等[2]应用数字图像处理技术,建立了包含集料、空隙和胶浆在内的沥青混合料有限元模型,并模拟研究了沥青混合料劈裂试验. Chen等[3]利用数字图像处理技术将计算机断层扫描图像转换为数字格式,并与有限元建模相结合,建立了二维沥青混合料数字模型,并进行了沥青混合料粘弹特性的研究.王端宜等[4]应用工业CT扫描获得沥青混合料的试件图像,结合有限元建模方法,建立了包含集料、空隙和胶浆三相体系的沥青混合料二维有限元模型,并进行了劈裂试验模拟.
一些学者采用基于体素的沥青混合料三维重构方法进行有限元虚拟力学研究,并取得一定的研究成果.万成等[5-6]根据沥青混合料三维重构原理,建立了三维数值试样,并对FAC-13混合料的3种不同级配数值试样进行单轴静载蠕变数值模拟,模拟结果与实际试验结果一致. Dai[7-8]基于图像像素的位置关系建立了二维与三维的数值试样,并对数值试样进行动态模量和相位角的有限元预估,结果显示所建立的有限元模型能够准确地预估了颗粒材料的粘弹性质.孙红红[9]通过MATLAB程序开发,基于体数据,建立了沥青混合料三维微观结构有限元模型,并进行有限元模拟计算,将模拟计算的结果与劈裂试验结果进行对比,证明了数值模型的合理性.汪海年等[10]利用X-ray CT技术,结合MATLAB程序完成沥青混合料的三维重构,用该模型进行数值模拟后的试验结果与室内试验结果有很好的吻合,验证了此重构方法的正确性.
然而,在沥青混合料数值建模过程中,在颗粒接触紧密的部位,由于颗粒与颗粒之间的间隔物质的密度对比度差异不是十分明显,对CT图像分割后,不可避免地出现相互接触的集料粘结现象.这种集料结构形式使得后面的虚拟力学过程中,粘连的集料被计算机识别成单个颗粒,导致计算结果与实际不符.因此,在数值建模前,必须对图像进行粘连分割处理.
目前,混合料粗集料粘连分割主要是采用人工手动处理[11-12].这种方法对单张图片处理较为方便,但是如果图片数量过多则费时费力,不利于图像快速高效地进行处理.因而一种粘连图像自动分割算法十分必要.粘连图像自动分割算法在医学细胞图像处理、农业谷物检测图像识别、字符识别等领域应用较广.分割算法主要包括利用轮廓信息的分割算法、利用椭圆拟合信息进行分割的算法、形态学方法等[13].这些算法都要求图像具有某些特定的性质.沥青混合料粗集料与具有相似形状和尺寸的细胞、谷物和字符等不同,一个沥青混合料级配中,集料的尺度差别较大.为了克服多尺度对象的粘连分割,文献[14]提出了一种基于形态学多尺度分割算法对细胞粘连颗粒进行分割,该算法首先将原图像分解成多尺度的标记图像,然后从最小尺度的标记图像开始重构目标物的形状和大小,同时使用形态学中的骨架产生分割线并保留它们,最终通过上述迭代重构的方法,产生正确的分割线.然而,在实际运用该算法对沥青混合料粗集料进行粘连图像分割时存在不足.由于细胞的尺度相似,可以通过不断尝试,确定了最佳结构元素大小后对重叠细胞进行腐蚀.但是,通过采用不同大小的结构元素作极限腐蚀叠加可以得到不同的距离图像,特别是对于沥青混合料粗集料这些大小和形状都存在很大的差异物质来说,单一的结构元素不能很好地减少集料的欠分割和过分割.
基于上述原因,本文提出一种基于改进形态学多尺度算法的集料粘连分割算法,此算法可以有效地抑制集料的欠分割和过分割.
1 数学形态学基本理论 1.1 膨胀与腐蚀数学形态学是以形态结构元素为基础对图像进行分析的数学工具,基本思想是用具有一定形态的结构元素去度量和提取图像中的对应形状以达到对图像分析和识别的目的.数学形态学的语言是集合论,膨胀与腐蚀是数学形态学中两个基本的运算.数学形态学上膨胀的定义为集合的运算, 作为Z2中的集合A和B,A被B膨胀表示为[15]
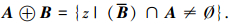
|
(1) |
作为Z2中的集合A和B,A被B腐蚀表示为[15]

|
(2) |
结构元素是膨胀和腐蚀操作的最基本组成部分.二位平面结构元素由像素为0或1的矩阵组成,结构元素的原点指定了图像中需要处理的像素范围,结构元素中数值为1的点决定结构元素的领域像素在进行膨胀或腐蚀操作时是否需要参与计算.数字图像中膨胀的具体操作是指采用一个半径为r的结构元素,扫描图像中的每一个像素,用结构元素中的每一个像素与其覆盖的像素作“与”操作,如果都为0,则该像素为0,否则为1.膨胀处理的结果是使原来的二值图像增加一圈.数字图像中腐蚀的具体操作是指采用一个半径为r的结构元素,扫描图像中的每一个像素,用结构元素中的每一个像素与其覆盖的像素作“与”操作,如果都为1,则该像素为1,否则为0.腐蚀处理的结果是使原来的二值图像减小一圈.
1.2 欧氏距离变换距离变换是对二值图像的一种操作运算,是将一幅二值图转化为一幅灰度图像,在这幅灰度图像中,每个像素的灰度级是该像素与距其最近的背景间的距离.根据距离类型的划分,距离变换可分为欧氏距离变换和非欧氏距离变换.其中欧氏距离变换的精度高,与实际距离相符,在数字图像处理中应用更广泛.一幅M×N的二值图像可以用一个二维数组AM×N=[aij]表示,其中aij=1的像素表示目标点,aij=0的像素表示背景点.图像上两点的坐标为(x, y)与(s, t),相对应的像素为p和q,则它们之间的欧氏距离变换定义为[10]
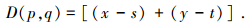
|
(3) |
数学形态学算法是将数学形态和算法相结合的一种新的分割思想.近年来,数学形态学算法逐渐发展成为一门新兴的图像分析科学,它着重研究图像的几何结构及相互关系.
文献[14]采用形态学多尺度算法对粘连细胞进行有效的分割,选用单一的结构元素进行极限腐蚀.然而,当选用的结构元素尺寸较小时,极限腐蚀对集料边界细微的变化较为敏感,容易造成过分割;当选用的结构元素尺寸较大时,极限腐蚀对集料边界的变化不敏感,容易造成欠分割.因此结构元素的选择尤其重要.
考虑到目前沥青混合料CT切片的分别率一般为1024像素×1024像素.结构元素半径太大时,导致膨胀后的粘连集料二值图像比原图像大很多,或者腐蚀粘连集料二值图像过程中原图像突然消失,这些现象会使得后面的计算结果与实际不符.因此,在大量的实践基础上,本研究选用4种半径尺寸逐渐递增的结构元素对图像进行极限腐蚀.在腐蚀前先对二值图在MATLAB环境下进行标记分类,这样可以防止较小集料被在后面的分割过程中过滤掉;然后选用最小尺寸结构元素对所有标记好的二值图分别进行极限腐蚀,在极限腐蚀过程中,二值图如果出现两个或以上的分割对象,则将其归类为可能粘连颗粒,以待下一步分析,如果不出现两个或者以上的分割对象,则可以认为此对象为独立颗粒.之后分别选用不同尺寸的结构元素作为极限腐蚀结构元素对可能是粘连颗粒二值图分别进行形态学算法的粘连分割.根据不同结构元素下的形态学算法得到的粘连分割图,以分割线数目出现频率最大的分割数作为此二值图的实际分割,并以最小的结构元素所对应的分割图像作为实际的分割图像.最后把所有经过分割的标记图像进行叠加,形成完整的粘连分割图像.
形态学多尺度算法流程见图 1,算法的步骤包括以下6步:1)将原始沥青混合料CT图像转为灰度图并滤除图像中文字和坐标轴信息,采用中值滤波滤除图像中的噪声,填充图片中的细小空洞,采用最大类间方差法(OTSU)对图像进行分割,最终形成集料的二值图. 2)在MATLAB环境下对集料二值图进行标记分类. 3)选择半径为1的圆形结构元素对二值图进行极限腐蚀,对在极限腐蚀过程中是否出现两个或以上的分割对象标记图像进行归类,出现两次或以上分割对象的标记为可能粘连颗粒,只有一个图像则标记为独立颗粒. 4)选择4种结构元素(半径r分别为1、2、3、4的圆形结构元素)分别进行形态学算法的粘连分割. 5)根据粘连分割后的图像,分别判断各个图像分割线的数目,以分割线数目出现频率最大的分割数作为此二值图的实际分割,并以最小的结构元素所对应的分割图像作为实际的分割图像. 6)叠加独立颗粒图像和经粘连分割后的图像,最终生成目标分割图像.
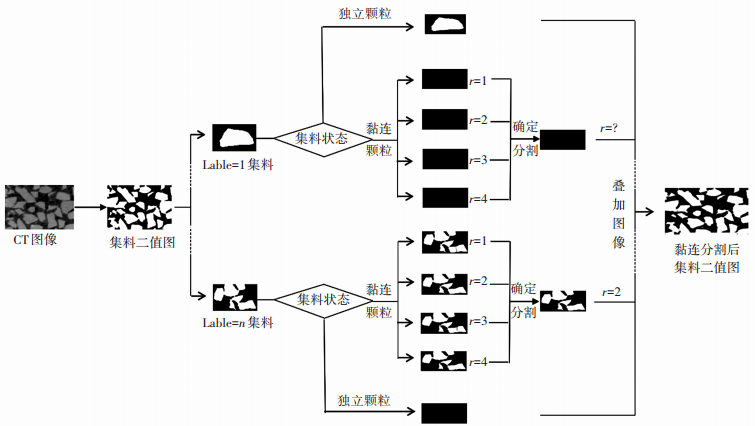
|
图 1 算法流程 |
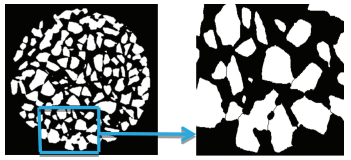
为了验证算法的有效性,分别采用文献[14]形态学多尺度算法与本研究提出的算法对沥青混合料CT扫面切片进行集料的粘连分割处理.应用德国YXLON公司生产的Compact-255型高精度工业CT扫描获得尺寸大小为1024像素×1024像素的AC-16沥青混合料切片,如图 2所示.分别采用两种算法对AC-16沥青混合料切片图像进行粘连分割处理[15],其对应的二值图见图 3、分割后图像见图 4,本文算法见图 5.

|
图 2 AC-16沥青混合料CT切片图像 |
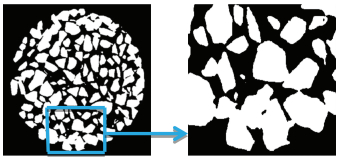
|
图 3 二值图 |

|
图 4 原算法分割图像 |
|
图 5 本文算法分割图像 |
运用人眼识别的方法,对粘连分割前的二值图中的颗粒个数进行统计.人眼识别的颗粒总数153个.两种算法分割后的粘连情况结果如表 1所示.
| 表 1 颗粒分割数据结果比较 |
颗粒过分割与欠分割的变化趋势见图 6.由图可知,原算法采用单一的结构元素进行极限腐蚀时,过分割的颗粒数量随着结构元素半径的增大而减少,这是因为选用尺寸较大的结构元素进行极限腐蚀时,极限腐蚀对集料边界的变化不够敏感,过分割现象较轻.欠分割现象恰好相反,由于采用半径较大的结构元素进行极限腐蚀时,集料边界变化较小的地方不能很好地识别,因此容易造成颗粒的欠分割.

|
图 6 颗粒过分割与欠分割变化趋势 |
对比本文算法的数据结果,采用本文提出的算法进行集料粘连分割产生的过分割准确率达到98%,与此同时,欠分割的准确率非常接近原算法采用最小结构元素所产生的欠分割准确率.所以,当同时考虑过分割与欠分割两种情况时,本文算法能比原算法获得更好的分割效果.
4 分割精度评价采用形态学原理对粘连颗粒分割时,由于对原图像进行一系列的腐蚀与膨胀的操作,使得分割后的颗粒大小与粘连分割前的颗粒大小存在一定的差异,如图 4所示.结构元素半径较大时,对原图像的粘连分割比较粗糙,分割后的颗粒面积变化大.
为了能够客观地对分割精度进行评价,以手动分割结果作为标准,将所用算法粘连分割后的颗粒面积与手动粘连分割后的颗粒面积的比值作为分割精度评价指标[16-17],定量地评价本文算法分割后的图像精度.根据大量的沥青混合料粗集料粘连分割经验可知,手动分割线上的像素总数相对粗集料的像素总数较少.因此,可以假设未进行分割前的集料像素总数与手动分割后集料的像素总数相同.本文将随机选用4张尺寸大小为1024像素×1024像素的AC-16沥青混合料切片进行粘连分割精度评价.不同算法得到的分割前后颗粒像素总数如表 2所示.
| 表 2 不同算法得到的分割前后颗粒像素总数 |
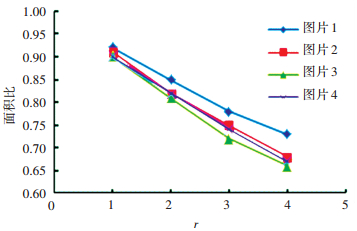
图 7表示选用不同半径的结构元素对4幅图片进行粘连分割后的面积比的发展趋势.由图可知,不论结构元素半径的大小是多少,面积比都小于1.这说明了采用形态学的方法对沥青混合料粗集料粘连图像进行分割,分割后的图像有一定程度的收缩.采用结构元素半径为1分割图像得到的面积比可以认为是最佳的面积比.面积比随着结构元素的半径的增大而减小.面积比越大,说明分割后的图像与原图像差别就越小.采用本文算法得到的面积比接近原算法元素半径为1的面积比.因此,运用本文算法分割粘连图像的精度较高.
|
图 7 颗粒面积比 |
1) 采用4种尺寸不同的结构元素对图像进行极限腐蚀,根据不同结构元素下的形态学算法得到的粘连分割图,以分割线数目出现频率最大的分割数作为此二值图的实际分割,并以最小的结构元素所对应的分割图像作为实际的分割图像,最后形成完整的粘连分割图像.
2) 运用所提出的算法对AC-16沥青混合料X-ray CT切片进行粘连分割,与原算法对比,能够获得较好的分割效果.并选用粘连分割后的颗粒面积与手动粘连分割后的颗粒面积的比值作为分割精度评价指标,对随机选用同一试件的4张CT切片分割精度评价,分割精度结果分析显示,改进的形态学多尺度算法分割粘连图像的精度较高.
3) 该算法弥补了传统分割算法不能有效分割粘连颗粒的不足,为三维数值试样建模奠定了基础.
| [1] |
张肖宁. 基于X-ray CT的沥青混合料计算机辅助设计技术的研究进展[J]. 交通科学与工程, 2010, 26(2): 1-8. |
| [2] |
虞将苗, 李晓军, 王端宜, 等. 基于计算机层析识别的沥青混合料有限元模型[J]. 长安大学学报, 2006, 26(1): 16-19. |
| [3] |
CHEN Peilin, YU Jiangmiao, LI Xiaojin, et al. Microstructural finite element analysis of asphalt mixture using digital image processing[J]. Journal of Anhui University of Technology, 2006, 23(3): 327-330. |
| [4] |
王端宜, 吴文亮, 张肖宁, 等. 基于数字图像处理和有限元建模方法的沥青混合料劈裂试验数值模拟[J]. 吉林大学学报, 2011, 41(4): 965-973. |
| [5] |
万成. 基于X-ray CT和有限元方法的沥青混合料三维重构与数值试验研究[D]. 广州: 华南理工大学, 2010.
|
| [6] |
万成, 张肖宁, 王邵怀, 等. 基于X-CT技术的沥青混合料三维数值化试样重建[J]. 公路交通科技, 2010, 27(11): 33-37. DOI:10.3969/j.issn.1002-0268.2010.11.006 |
| [7] |
DAI Q. Prediction of dynamic modulus and phase angle of stone-based composite using micromechanical finite element approach[J]. Journal of Materials in Civil Engineering, 2010, 22(6): 618-627. DOI:10.1061/(ASCE)MT.1943-5533.0000062 |
| [8] |
DAI Q. Two-and three-dimensional micromechanical viscoelastic finite element modeling of stone-based materials with X-ray computed tomography images[J]. Construction and Building Materials, 2011, 25(2): 1102-1114. DOI:10.1016/j.conbuildmat.2010.06.066 |
| [9] |
孙红红. 基于CT图像沥青混合料三维有限元数值模拟研究[D]. 西安: 西安建筑科技大学, 2012.
|
| [10] |
汪海年, 黄志涵, 李磊, 等. 基于X-ray CT的沥青混合料三维重构方法[J]. 中国科技论文, 2013, 8(11): 1115-1118. DOI:10.3969/j.issn.2095-2783.2013.11.009 |
| [11] |
徐文杰, 岳中琦, 胡瑞林. 基于数字图像的土、岩和混凝土内部结构定量分析和力学数值计算的研究进展[J]. 工程地质学报, 2007, 15(3): 289-313. |
| [12] |
COLERI E, HARVEY J T, YANG K, et al. Investigation of asphalt concrete rutting mechanisms by X-ray computed tomography imaging and micromechanical finite element modeling[J]. Materials and Structures, 2013, 46(6): 1027-1043. DOI:10.1617/s11527-012-9951-x |
| [13] |
牛杰, 卜雄洙, 钱堃. 利用骨架特征信息的粘连谷粒图像分割方法[J]. 农业机械学报, 2014, 45(9): 280-284. DOI:10.6041/j.issn.1000-1298.2014.09.045 |
| [14] |
SCHMITT O, HASSE M. Morphological multiscale decomposition of connected regions with emphasis on cell clusters[J]. Computer Vision and Image Understanding, 2009, 113(2): 188-201. DOI:10.1016/j.cviu.2008.08.011 |
| [15] |
冈萨雷斯. 数字图像处理[M]. 3版. 北京: 电子工业出版社, 2001.
|
| [16] |
徐科. 用于沥青混合料的数字图像处理技术及其应用研究[D]. 广州: 华南理工大学, 2006.
|
| [17] |
刘佳辉, 李智. 沥青混合料CT图像分割技术及其效果分析[J]. 重庆交通大学学报(自然科学版), 2011, 30(6): 1335-1338. |
 2016, Vol. 48
2016, Vol. 48




