为缓解日益严重的城市交通问题,许多城市兴建了地铁设施,同时城市发展需要建造深基础高层建筑,由于桩基础的施工和承受荷载过程会造成周围土体的位移和应力变化,进而也会影响邻近的隧道.为确保已建地铁的正常运营,地铁管理部门制定了严格限制条例来控制地铁隧道两侧的工程活动.一般说来,对于隧道附近的桩基,为避免打入桩的挤土、振动效应,都是采用钻孔灌注桩形式,在桩基施工完毕,桩基础逐步承担上部荷载,在垂直载荷下,桩基础会产生竖向沉降,并且会带动周围土体的竖向及水平向变形,对于距离桩基础较近的运营隧道,会产生附加的变形及应力.文献[1]就近距离桩和群桩施工过程和加载过程对隧道性状的影响进行了研究.文献[2-4]运用有限元程序对钻孔灌注桩的施工及受荷过程对已存隧道的受力和变形进行了分析.文献[5]借助有限元程序分析计算了上海太平洋期广场工程对邻近地铁1号线隧道的影响.文献[6]应用所研发软件计算分析了桩筏基础蠕变对邻近隧道的影响规律并总结了隧道影响因子的作用.文献[7]采用群桩基础共同作用的分析方法,考虑了孔底沉渣的影响,对钻孔灌注桩基础跨越地铁隧道线可能带来的影响进行了计算分析.文献[8]考虑到了桩间加筋和遮拦效应的影响,以剪切位移法为基础,分析超深群桩在工作荷载下对邻近土体应力状态和已有隧道沉降的影响.近年来,文献[9-11]针对不同的工程实例,运用三维有限元数值模型,模拟了桩基础的成孔施工、运营期桩基承担荷载在土中产生的应力扩散对既有隧道结构和轨道变形产生的影响.对已有相关文献分析可以看出,由于受制于数值分析研究手段,且桩基施工及承载过程对己有隧道影响的相关实测数据很少,使得针对邻近隧道桩基建设活动的限制条例的客观性得不到相应的验证.基于桩基承载对地铁隧道影响机制的空间与时间分布特征可以在土工离心模型试验中有效实现,本文借助长安大学土工离心机,结合实际工程案例,阐明承载过程桩基-土-隧道之间相互影响机制,可为类似工程的设计与施工提供借鉴.
1 离心模型试验分析 1.1 试验工程背景拟建西安东环广场建设项目, 地上由塔楼和裙房组成,其中塔楼41层,主屋面高度179.8 m,裙房7层,主屋面高度为38.20 m.拟建项目裙房位于西安地铁隧道1#线上方,为减小建筑对隧道结构的附加荷载,裙房采用跨越式布置,即在地下一层采用大跨度转换结构,将上部结构荷载通过桩基础传递到隧道下部的土层,桩端持力层选在第7层卵石持力层上,该土层顶面距离隧道结构底面约16 m,桩长32~36 m,该工程裙房部分地基基础设计方案及地铁隧道的位置关系如图 1所示,裙房基础桩直径为1 m,桩位距隧道较近,一般位于隧道外围2 m范围之外,3 m范围之内,柱荷载按照上部结构计算提供的值,其最大桩顶部荷载为3.6×104 kN.

|
图 1 地铁隧道模型 |
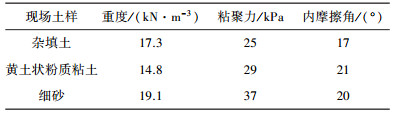
本次试验使用的模型箱长宽高分别为700、360、500 mm.试验用土取自西安东环广场建设项目工地,土体基本物理力学参数如表 1所示.试验模型中地层共分为3层:第1层土厚度5 cm,用密实砂土用来模拟桩基持力层;第2层土厚35 cm,为地铁隧道所在土层,为粉质粘土,中间粒径 D50= 122 μm,土粒密度 Gs= 2.27 kg/m3,从现场取回土样后晒干筛分并重新制备成饱和状态,其含水量 w= 29.9%;第3层土厚5 cm,主要为杂填土,控制含水量为 w= 17.5%.试验所用隧道基本材质为有机玻璃,其弹性模量为6 GPa,泊松比为0.3,模型管直径拟为100 mm,壁厚10 mm,如图 1所示.模型试验相似比例 N= 60,根据模型试验相似理论[12],制定相似法则见表 2,有机玻璃材质隧道模型相当于原型中厚度为350 mm的混凝土管片盾构隧道(弹性模量为30 GPa).
| 表 1 土体物理力学参数 |
| 表 2 离心试验相似法则 |
模型桩材质为圆柱形铝质金属管,直径 Dpi 为10 mm.本次模型试验重点考虑桩周摩阻力在桩周土中传递过程对近距离隧道结构的影响,为使模型桩端承于隧道下方细砂持力层中,故设计模型桩长42 cm;试验分别考虑桩隧距径比 xpil /Dt 为0.89和1.06两种情况,模拟实际桩隧间距2 m和3 m时,桩周摩阻力所引发的隧道附加影响,每种桩隧间距分别考虑单侧和双侧两种布桩方式.
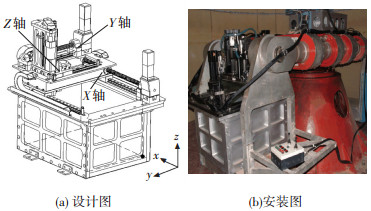
1.3 离心场桩基加载过程为了模拟桩基加荷过程,试验中运用长安大学土工离心机加荷载系统,该系统由机械手主机和电气系统构成,以机械手模型箱内部右下角为坐标原点,如图 2所示,X 向运行距离为207~587 mm,Y 向运行距离为217~467 mm,Z 向运距离为495~895 mm.其中 Z 向轴能提供最大18 kN的垂直荷载,利用 Z 轴的拉压功能可有效模拟压桩及施加荷载过程.本次模型试验过程中,机械手 Z 轴先向桩基轴向施加轴向荷载将模型桩预压至预定桩位,然后将桩顶荷载保持在3种荷载 p 分别为5 kN(相当于原型1.8×104 kN)、10 kN和15 kN,每级加荷后分别保持离心机运转2.4 h(相当于原型固结360 d).
|
图 2 土工离心机机械手系统 |
地铁隧道模型分别进行横向布置和纵向布置,如图 3所示.

|
图 3 试验测试装置布置 |
由于本次试验主要考虑地铁隧道横向变形,考虑到隧道结构纵向长度方向上隧道刚度效应所对模型试验结果的影响,试验中横向布置隧道模型长度为660 mm,如图 3(a)所示.横向布置隧道布设两个监测断面,分别为断面 A和断面B,截面A 共设8个弯矩测点(编号为S1~S8),沿截面周长平均分布;截面 B 周围均匀设置8个土压力测点(编号为E1~E8),测量隧道周边土压力的变化.弯矩的量测通过贴在管片上下表面的4个应变片组成的全桥电路来实现,土压力采用通用的微型土压力计进行量测.同时为分析桩基础承载过程对地铁隧道沉降的影响,在断面 A 隧道模型的顶部、拱腰和底部分别布设4个激光位移传感器测点.为有效获取桩基承受荷载时桩周和隧道界面间土体位移场分布,隧道模型纵向布置(模型长度为350 mm)如图 3(b)所示,在桩基础荷载影响区范围内纵横方向画设纵横经纬线,并以纵横线交汇处为基准点,纵横间距为20 mm×20 mm,利用土工离心机高速摄像设备获取不同时段各基准点变形后纵横坐标值,通过坐标变化来绘制各测点横向和纵向位移变化值.
2 试验结果分析 2.1 隧道变形分析根据激光位移传感器测试数据结合图像位移处理结果绘制了桩顶施荷后10个月后隧道轮廓变形图,见图 4.
|
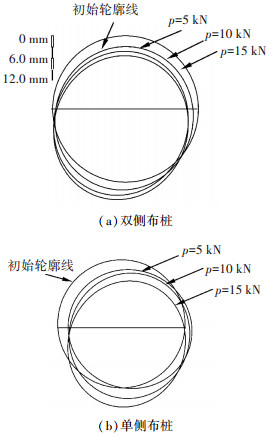
图 4 隧道轮廓变形图 |
从图 4可以看出,伴随着桩基承载,隧道结构发生了整体的下沉和变形,变形以沉降为主,水平位移较小,换算为实际模型,隧道最大沉降量为7.695 mm,最大水平位移为2.42 mm.拱顶下沉量随着桩顶部荷载的增加而增加,当桩顶部荷载达到10 kN时(相当于原型3.6×104 kN),拱顶最大下沉将量达到3.8 mm,当桩顶部荷载达到15 kN时(相当于原型5.4×104 kN),拱顶最大下沉将量达到6 mm. 图 4(b)为左单侧加宽轮廓图,隧道轮廓变化图明显不对称,总体显示隧道圆周沿隧顶顺时针145°处变形值最大达到最大值,侧向变形最大值达到了4.1 mm.说明由于桩隧间的土体传递了桩周摩擦力,相对于隧道双侧布置桩基础,单侧布桩隧身发生扭曲变形的可能性更大.因此,对于实际运营的地铁隧道,如果隧道结构单侧桩基施工扰动,更需要对隧道结构的变形进行实时有效监测.
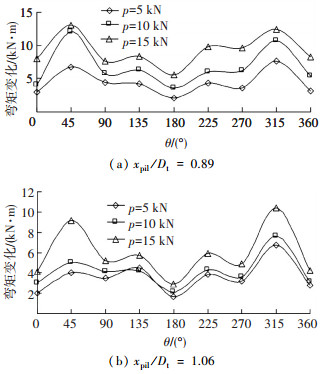
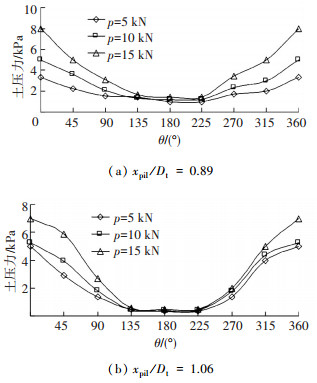
2.2 隧道受力变化分析以地铁隧道拱顶为零角度,θ 角顺时针转动,绘制桩基础加载前后隧道圆周的弯矩变化分布如图 5所示.由图 5可以看出,当隧道两侧均有桩基存在时,弯矩较大值位于拱顶区域 (0° < θ < 90° 和 270° < θ < 360°),弯矩值最大附加增加量为12.78 kN·m,比较图 5(a)和图 5(b),当桩隧距径比 xpil /Dt 由0.89变化为1.06时,弯矩值最大附加增加量减小到9 kN·m左右.土压力变化值如图 6所示,土压力变化最大值出现在拱顶及两侧拱腰部区域,最大变化值达到8.14 kPa,隧道结构圆周水平面以下 (90 < θ < 270°) 土压力的变化值都比较小,比较图 6(a)和图 6(b),测试结果显示类似变化趋势,具体表现为有桩基荷载作用条件下,所获得最大弯矩均比无桩情况相同位置的测试值要高,相应附加土压力则与无桩情况的也有一定增加,但数值很小,对于隧道结构本身影响不大.
|
图 5 模型隧道截面A弯矩改变值 |
|
图 6 模型隧道截面B在土压力改变值 |
以往关于桩基隧道相互作用研究中,闫雅静[13]假定隧道为弹性地基无限长梁,并认为隧道的位移曲线形式与隧道所在位置土体的位移曲线形式一致,都呈近似的高斯曲线分布.廖少明等[14]通过假定隧道的位移曲线与土体的位移曲线相似,将两者方程代入一维弹性地基梁的平衡方程中求解得到了隧道位移曲线.为了进一步研究桩-土-隧道结构之间相互作用机理,基于试验过程所获得的图像位移数据计算并绘制了土体各点的剪应变值,最大剪应变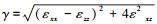
|
图 7 桩周土体最大剪应变 |
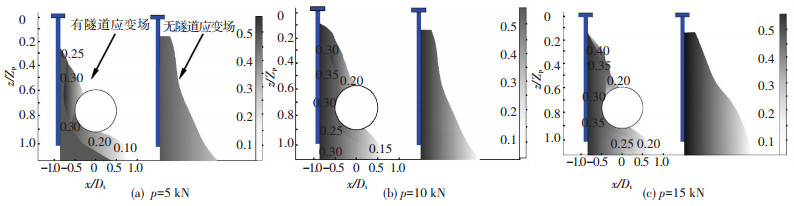
图 8给出了不同桩顶荷载下,隧道与桩基础之间土体剪切应变等值线图,可以看出,桩周土体在摩阻力的作用下发生剪切应变,但由于隧道结构在土体中的加筋遮拦效应,使得剪切应变发生了规律性的改变,这在隧道拱腰位置表现的更为明显;另外,比较不同桩顶荷载情况还可以看出,且随桩顶荷载的增加,加筋遮拦效应也越发明,隧道周边剪应变增幅明显.

|
图 8 隧道周边土体剪应变等值线 |
1) 隧道结构会在承载桩周所产生的附加应力场中产生加筋阻拦效应,明显缓释桩周摩阻力在相同位置处的传递,桩顶荷载越大,缓释的程度越明显;桩基承载过程会引发临近地铁隧道结构的下沉和水平变位,随着桩与隧道净距比 xpil /Dt 的增加,隧道拱顶下沉量以及弯矩变化最大值相应减小.
2) 桩基础承载所引发附加应力会在隧道结构体产生应力集中效应,隧道拱腰部位是桩基受荷所引发土体附加荷载主要承受区;相对于隧道双侧存在承载桩基础,单侧桩基础造成隧道所受弯矩分布向桩基础方向发生明显偏转,同时隧道整体结构向桩基础方向产生扭曲.
| [1] |
BENTON L J, PHILLIPS A. The behavior of two tunnels beneath a building on build foundation[C]//Deformation of Soils and Displacements of Structures. Florence: XECSMFE, 1991: 665-668.
|
| [2] |
SCHROEDER F C, POTTS D M, ADDENBROOKE T I. The influence of pile group loading on existing tunnels[J]. Geotechnique, 2004, 54(6): 351-362. DOI:10.1680/geot.2004.54.6.351 |
| [3] |
SCHROEDER F C. The influence of bored piles on existing tunnels[D]. London: Imperial College, University of London, 2003.
|
| [4] |
SCHROEDER F C. The influence of bored piles on existing tunnels:a case study[J]. Ground Engineering, 2002, 55(7): 32-34. |
| [5] |
闫静雅, 张子新, 黄宏伟, 等. 桩基础荷载对邻近已有隧道影响的有限元分析[J]. 岩土力学, 2008, 29(9): 2508-2514. |
| [6] |
关安峰. 桩基础对邻近隧道变形长期影响研究[D]. 上海: 同济大学, 2000.
|
| [7] |
楼晓明, 金志靖. 钻孔灌注桩基础对紧邻地铁隧道产生竖向附加应力和变形的计算分析[J]. 岩土力学, 1996, 17(3): 48-53. |
| [8] |
李镜培, 王昆. 超深群桩对邻近已有隧道的影响研究[J]. 岩土工程学报, 2011, 29(增刊2): 128-134. |
| [9] |
路平, 郑刚. 立交桥桩基础施工及运营期对既有隧道影响的研究[J]. 岩土工程学报, 2013, 35(增刊2): 923-927. |
| [10] |
黄晓阳. 桩基础荷载对既有地铁隧道的受力和变形影响分析[D]. 长沙: 中南大学, 2010. http://cdmd.cnki.com.cn/Article/CDMD-10533-1011180265.htm
|
| [11] |
沈志刚. 超高层建筑结构构筑及使用阶段对紧邻地铁运营隧道的影响分析[D]. 北京: 北京交通大学, 2014. http://cdmd.cnki.com.cn/Article/CDMD-10004-1014401071.htm
|
| [12] |
TAYLOR R N. Geotechnical centrifuge technology[M]. London: An Imprint of Chapman & Hall, 1995: 38-43.
|
| [13] |
闫静雅. 桩基础全寿命期对邻近已有隧道的影响研究[D]. 上海: 同济大学, 2007. http://cdmd.cnki.com.cn/Article/CDMD-10247-2007223037.htm
|
| [14] |
廖少明, 侯学渊, 彭芳乐. 隧道纵向剪切传递效应及其一维解析[J]. 岩石力学与工程学报, 2005, 24(7): 1110-1116. |
 2016, Vol. 48
2016, Vol. 48