矩形中厚板是一种常见的结构形式,广泛应用于公路、建筑、航天等领域,实际工程中有很多问题都可以简化为中厚板的弯曲问题,而随着现代工业的发展,对板结构的分析也提出了更高的要求,因此,更为准确的研究中厚板的弯曲具有十分重要的理论和实际意义.
目前,处理复杂板问题的流行办法是,采用数值方法来求解问题的数值解,其中具有代表性的方法包括有限差分法[1]、有限元法[2]等,但数值解的本质是近似解而非精确解,所以在数值解法不断发展的同时,学者们也针对板问题的解析解进行了进一步研究,并提出了一些新的求解办法,例如黄义等[3]采用变分解法,对于弹性地基上四边自由矩形板的弯曲问题进行了求解.钟阳等[4]建立了矩形中厚板Hamilton体系的构造方法,发展了矩形薄板和中厚板弯曲问题的辛几何解法.另外,钟阳等[5]还采用有限积分变换法求解了部分边界条件下的矩形薄板和中厚板问题.
本文采用的是改进的重三角级数法,来求解Mindlin板弯曲问题控制方程,求解过程中采用了解耦法,先通过引入新变量,将原来的二阶偏微分方程组,解耦为4个独立的偏微分方程,再以改进的重三角级数法,来分别求解完全独立的方程,进而简化了求解过程.
1 Mindlin板控制方程以及方程的解耦Mindlin板弯曲问题控制方程为
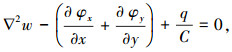
|
(1) |
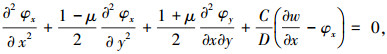
|
(2) |
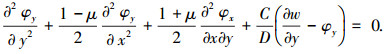
|
(3) |
该方程组以弹性理论为基础建立.其中▽2= 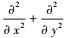
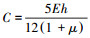

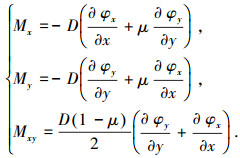
|
(4) |
其中Mx、My分别为垂直于x、y轴截面上的弯矩;Mxy为扭矩.控制方程1~3为耦合的二阶偏微分方程组,求其解非常困难.为了简化求解过程,首先对耦合偏微分方程(1)~(3)进行解耦,根据式(1)的基本形式,令
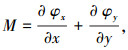
|
(5) |
进而,分别对式(1)进行改写,将式(2)对x求导,将式(3)对y求导相加,经过整理得到

|
(6) |
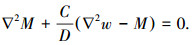
|
(7) |
又由式(6)、(7)括号内变量,得到

|
(8) |
进一步,对式(6)中作用算子▽2,并与式(8)相加,便得到关于已知荷载函数的独立方程为
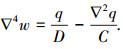
|
(9) |
再对式(1)分别进行x和y的求导,得到

|
(10) |
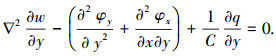
|
(11) |
将式(10)乘以系数(1+μ)/2,再与式(2)作相减,消去方程中的φy项,得到w与φx的独立关系表达式为

|
(12) |
其中常系数Q=2C/[D(1-μ)].同理,由式(11)乘以系数(1-μ)/2,和式(3)作相减,消去方程中的φx项,得到w与φy的独立关系表达式为

|
(13) |
再由式(6),对式(12)、(13)中的括号内变量进一步简写,得

|
(14) |

|
(15) |
至此,求解Mindlin板弯曲问题控制方程组,可以归结为分别求解独立方程(8)、(9)、(14)、(15).其中式(8)、(9)分别为关于w和M的独立偏微分方程,求其解的过程会大大简化于式(1)~(3)所表示的耦合二阶偏微分方程组.
2 问题的求解为了求得四边固支Mindlin板弯曲问题的解析解.本文利用改进的重三角级数法,对解耦的方程组展开求解,四边固支边界条件表达式为
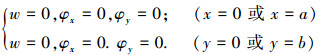
|
(16) |
根据边界条件表达式,设3个广义位移变量w、φx和φy的重三角级数解的基本形式为
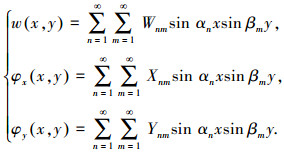
|
(17) |
其中αn=nπ/a,βm=mπ/b.另外根据M的定义表达式(5),故不妨也设M的重三角级数解形式为

|
(18) |
将外荷载q也进行双重正弦级数展开,可以得到

|
(19) |
其中Qnm为傅里叶积分常数.
将式(18)、(19)代入到关于M的独立偏微分方程(8)中,得到
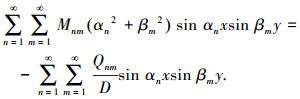
|
(20) |
由级数展开的唯一性定理,等式成立则等式两端级数项前系数相等,故解得
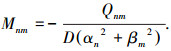
|
(21) |
将式(21)代回式(18)中, 得到M的级数解表达式为
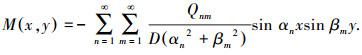
|
(22) |
同理将式(17)和式(22)代入式(9)中,得到w的级数解表达式为

|
(23) |
至此,就求得了M和w的级数解(22)、(23),然后将它们分别代入式(14)、(15)中,得到
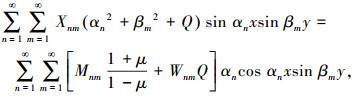
|
(24) |
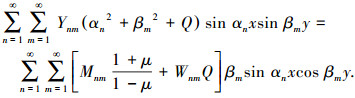
|
(25) |
其中Mnm和Wnm已求得.
显然,等式(24)、(25)两侧的级数核不同,不可以直接使用级数展开的唯一性定理,来求得项前系数Xnm和Ynm,故使用改进的重三角级数法,利用级数核的变换关系为
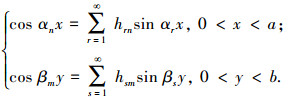
|
(26) |
其中

|
将上述级数变换关系代入式(24)、(25),经整理得到

|
(27) |

|
(28) |
从而经过级数核的变换,等式两端级数形式统一,再由级数展开的唯一性定理,直接解得项前系数Xnm和Ynm分别为
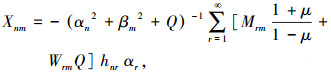
|
(29) |
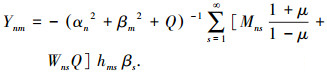
|
(30) |
将式(29)、(30)代入式(17),即求得所有广义位移变量φx和φy的级数解表达式为
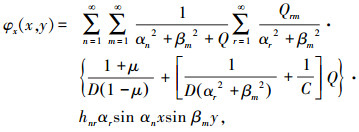
|
(31) |

|
(32) |
再由广义位移与内力的关系式,便可以求得弯矩Mx和My表达式分别为
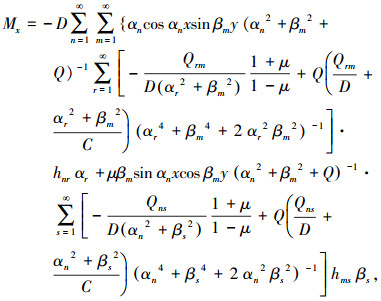
|
(33) |
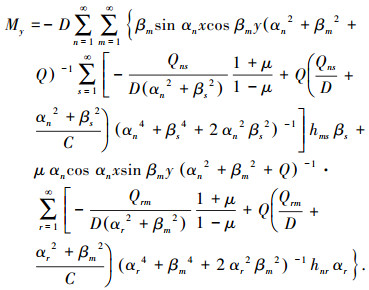
|
(34) |
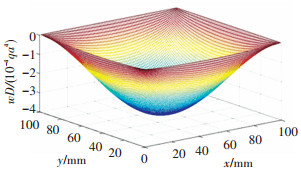
为验证本方法的正确性,以四边固支均布荷载作用下的矩形中厚板为例,取板的尺寸a=b,泊松比μ=0.3,设δ=a/h为板的边长厚度比. 图 1为δ= 3时矩形中厚板弯曲问题挠度无量纲化变化情况示意图.
|
图 1 矩形中厚板弯曲问题挠度变化情况 |
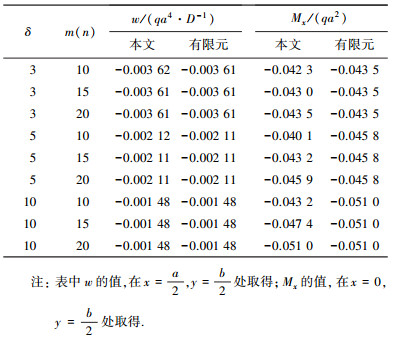
表 1中列出了算例条件下,中厚板中点挠度以及固支边中点弯矩的数值求解结果.结果表明,除δ= 5时的弯矩解析解与有限元解存在0.2%的相对误差外,在级数项m, n取至30时,本文所得的其他解析结果与有限元结果基本一致,从而可以证明本方法及推导的正确性.另外,通过解析解还可以研究剪切变形占总变形比例随板厚度的变化情况,从而探讨板种类的划分问题,相关内容会在之后的工作中具体讨论.
| 表 1 中厚板的挠度与弯矩解析解 |
1) 采用解耦法和改进的重三角级数法,求解了四边固支条件下矩形中厚板弯曲问题的解析解,在本文最后的算例中,将所得结果与有限元软件计算结果进行了对比,通过比对结果,证明了本文方法及推导的正确性.
2) 在求解的过程中,由于解耦法的使用避免了复杂的推导运算,大大简化了推导及计算过程;此外,该解耦方法还可以推广到其他板问题,用于简化相关解析解的求解过程.
| [1] |
NASH W. Several approximate analysis of the bending of a rectangular cantilever plate by uniform normal pressure[J]. Journal of Applied Mechanics-Transactions of the ASME, 1952, 19(1): 33-36. |
| [2] |
监凯维奇. 有限元方法基础理论[M]. 2版.北京: 世界图书出版社, 2008.
|
| [3] |
WANG M G, HUANG Y. Rectangular plates on elastic half a space[J]. Journal of Applied Mechanics, 1994, 11(4): 120-127. |
| [4] |
ZHONG Yang, LI Rui. Exact bending analysis of fully clamped rectangular thin plates subjected to arbitrary loads[J]. Mechanics Research Communications, 2009, 36(6): 707-714. DOI:10.1016/j.mechrescom.2009.04.001 |
| [5] |
ZHONG Yang, TIAN Bin. The analysis of free rectangular thick plates with finite integral transform method on elastic foundation[J]. Journal of Geotechnical Engineering, 2006, 28(11): 2019-2021. |
 2016, Vol. 48
2016, Vol. 48