2. 成都市事故预防处, 610031 成都
2. Accident Prevention Office, Bureau of Public Security of Chengdu Municipality, 610031 Chengdu, China
车载信息系统(如GPS导航,实时通讯,车载音视频)的普遍使用,以及交通控制信息的复杂性增加,使得驾驶员脑力负荷量增长[1].高脑力负荷状况,将造成驾驶员对突发交通事件反应时延长,周边交通事件识别率降低,从而引起反应操作失误,影响驾驶安全[2-3].因此对于驾驶员脑力负荷水平予以有效识别是驾驶行为类研究的一个关键性问题.目前国内外对驾驶员脑力负荷进行了广泛研究,研究表明车流量、交通标志、道路设计等交通环境因素会造成驾驶员脑力负荷量的增加,而脑力负荷的增加将会引起驾驶员对突发事件反应时间的延长,对外周随机信号、事件准确识别率的下降,以及车辆驾驶控制绩效的降低,从而引发事故发生概率的增加[4-7].为此,众多学者就驾驶脑力负荷测评方法开展了研究[8-10],目前主要采用的脑力负荷测评方法是基于NASA任务负荷指数和主观负荷评估技术的主观测评法,以及基于主任务和次任务行为绩效的工作绩效测量法.上述研究为驾驶员脑力负荷识别研究提供了重要依据.但主观测评及行为绩效测评具有与行为状态的时间滞后性,很难用于实时驾驶脑力负荷测评.脑电信号作为直接反应大脑活动的神经生理信号,与驾驶员的当前精神状态具有高度相关性[11-12],因此本研究拟以脑电神经信号为测评参量,基于SVM模型构建驾驶脑力负荷识别模型,以期实现驾驶员脑力负荷水平的动态实时识别,为自动辅助驾驶的设计以及交通信息的整合优化设计提供依据.
1 驾驶脑力负荷等级测定驾驶脑力负荷是指驾驶员在驾驶过程中大脑所承担的信息处理负荷量[13].目前脑力负荷测量与评价方法主要分为两种:1)主观量表法,该类方法让作业者依据脑力负荷量表,根据作业任务的脑力负荷量给出主观测评,主要采用的脑力负荷量表为NASA-TLX、SWAT、CH、MCH、OW等,其中前两种为多维度量表,后3种为单维度量表. 2)客观行为指标测评法,该类方法通常采用双任务实验范式,即要求驾驶员在完成主驾驶任务的同时,完成次要任务(如对周边随机探测信号反应,问题回答或加减运算).
基于上述脑力负荷测定分级方法,结合驾驶任务的特点,本研究拟采用主观测评、与驾驶主次任务行为绩效测定相结合的方式来确定脑力负荷等级.即在驾驶任务测试中记录驾驶员对主任务、次任务的行为绩效,通过不同脑力负荷下绩效水平对比来确定驾驶脑力负荷水平.此外,实验结束后,让驾驶员凭主观负荷感受,填写NASA量表给出主观脑力负荷分数.
2 基于脑电信号的脑力负荷识别模型构建 2.1 脑电信号参数计算脑电信号反映了大脑活动状态,人脑由低负荷状态进入高负荷状态时,脑电活动频段幅值也相应发生变化,即高频波段幅度增加而低频波段幅度降低.脑电活动的各频段幅值变化能反映驾驶员的脑力负荷状态[11-13].因此,可以将脑电4种信号频段 δ (0.5~4 Hz), θ (4~8 Hz), α (8~13 Hz), β (13~30 Hz)幅值作为脑力负荷识别参数[14].对于一个电极的脑电信号参数计算过程如下.
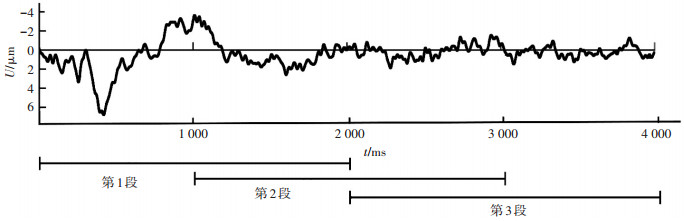
1) 以1 min脑电信号作为基本分析单元,对1 min脑电信号以 0~ 80 Hz为带宽整体进行滤波处理.对于脑电信号设定重叠率为50%、步长为2 000 ms的时间窗,从左至右逐段分割,共得到59个时间窗,如图 1所示.
|
图 1 脑电信号分段示意 |
2) 对于一个时间窗口内的脑电信号 f[n] 进行快速傅里叶变换,得到该脑电信号 f[n] 在频域上的幅值分布 f[k],即
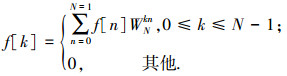
|
(1) |
式中: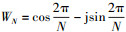
3) 按照 δ (0.5~4 Hz), θ (4~8 Hz), α (8~13 Hz), β (13~30 Hz)从 f[k] 中提取出4种波幅度序列,去除该序列中均值正负3倍标准差外的异常数据后求均值,得到4个波段在一个时间窗内的幅值,再对59个时间窗幅值求均值,以该平均值作为此1 min脑电信号该频段幅度代表值.
同理对于 q 个电极的脑电信号,均采用上述方法进行处理,则相应得到 4×q 项脑电参数,记为 xj(1≤j≤4×q).
2.2 驾驶脑力负荷特征指标选取为提高识别精度,同时减少特征向量维度,降低数据运算负荷量,需从上述 4×q 项脑电参数中,选取若干参数作为驾驶脑力负荷特征指标.具体做法为,对于任意的一项参数 xj,将其在高脑力负荷驾驶状态与低脑力负荷驾驶状态下得到的参数序列进行混合,进行Kruskal-Wallis检验,即
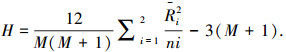
|
(2) |
式中:H 为检验统计量;i 为脑力负荷等级标量 ,i=1 为低负荷,i=2 为高负荷;Ri 为第 i 类负荷等级下参数样本的平均秩;M 为两类参数样本的总量.
由于 H 服从自由度为1的卡方分布,查表可得临界区域的概率 p. p值代表了两种脑力负荷条件下样本分布相同的概率,故p值越小代表该项参数在两类负荷状态下的数据分布差异越大,p < 0.05即为差异显著. 基于上述方法,对 4×q 项脑电参数逐一进行检验,从 4×q 项脑电参数中选出差异最为显著的 m(1≤m≤4×q) 项构成驾驶脑力负荷特征指标.
3 基于SVM的辨识器构造设驾驶员的第 t 个脑力负荷识别特征指标样本为 xt=(xt1, xt2…, xtm),其中 t=1,2,…,D,D为样本容量.若设定1为高脑力负荷,-1为低脑力负荷,则xt 可能是1或-1两种类型中的其中一种.通过非线性变换 Φ,将xt 映射到高维线性空间,若存在最优线性分界面满足
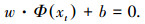
|
(3) |
其中 w·Φ(xt) 为向量 w 和 Φ(xt) 的内积.则得到判别函数
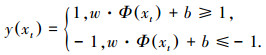
|
(4) |
该问题可转化为二次规划问题
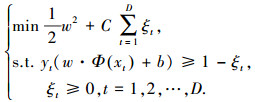
|
(5) |
其中:w∈RD 和 b∈R 为权重因子;ξt 为松弛函数;C 为惩罚函数. Φ(xt) 可以用核函数 K(xt, xl)=exp(-(xt-xl)/σ2)(σ为核函数的宽度, t、l=1,2,…,D) 来代替,故决策函数写为
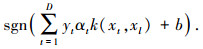
|
(6) |
对于一个未知类型的驾驶员脑力负荷识别特征向量样本 x=(x1, x2, …, xm),计算
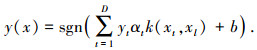
|
(7) |
若 y(x)=1,判断 x 属于第1类;若 y(x)=-1,判断 x 属于第2类.
4 识别效果测评SVM识别模型对某个未知类型的驾驶员脑力负荷识别特征向量样本 X={x1, x2, …, xq} 的识别可产生4种结果:1)输入样本为高脑力负荷,识别判断为高脑力负荷,记为真高负荷;2)输入样本为低脑力负荷,识别判断为高负荷,记为伪高负荷;3)输入样本为低脑力负荷,识别判断为低脑力负荷,记为真低负荷;4)输入样本为高负荷,识别判断为低负荷,记为伪低负荷.基于上述假设,可构建以下3项指标对识别效果予以测评,即
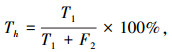
|
(8) |
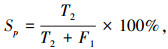
|
(9) |
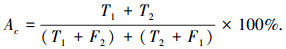
|
(10) |
式中:T1 为真高负荷样本量;T2 为真低负荷样本量;F1 为伪高负荷样本量;F2 为伪低负荷样本量;Th 为SVM模型对高脑力负荷状态的识别正确率;Sp 为SVM模型对低脑力负荷的识别正确率;Ac 为SVM模型对所有样本的整体识别正确率.
5 实例步骤1 实验设计.选取16名被试在模拟器(合纵连横VDS-S-Ⅲ)上分别进行高低负荷驾驶测试实验.被试年龄为24±2岁,持有效驾照,驾驶里程累计10 000 km以上, 测试场景如图 2所示.

|
图 2 模拟实验 |
采用双任务实验范式构造高、低两种条件的驾驶脑力负荷等级,其中主任务为驾驶追踪任务,实验前告知被试两车间距的合理值,通过练习使被试感知合理距离.任务要求驾驶员控制A车,与B车保持合理间距.次任务为随机信号探测任务,当B车突然制动,刹车灯亮起,要求被试尽可能快地做出制动反应,此时仍需保持合理间距.任务负荷由主任务的追踪速度来控制,高负荷平均车速为80 km/h,低负荷平均车速为40 km/h[15].
在实验过程种,记录两种脑力负荷条件下A、B两车实际间距与合理间距的差值和对随机探测信号任务的反应时及正确率,数据记录频率为10 Hz.同时,采用德国Brain Products公司EEG记录与分析系统,按国际10~20系统扩展的32导电极帽记录驾驶员脑电数据,头皮与电极之间的阻抗小于5 kΩ,记录带宽为0.5~100 Hz,采样率为1 000 Hz.
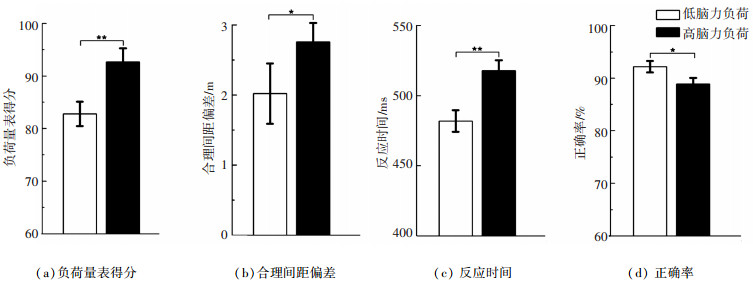
步骤2 脑力负荷分级验证.对实验中3项行为数据及主观负荷测评数据进行均值与标准差计算其结果如图 3所示.
|
图 3 行为数据结果 |
对上述数据进行配对样本t检验,结果表明,NASA主观量表得分在低负荷下显著低于高负荷(82.20/92.70,t(15)=-8.197,p < 0.01)低负荷条件下两车合理距离偏差值与反应时显著低于高负荷条件(2.02/2.76,t(15)=-2.40,p < 0.05; 482.5/518.6,t(15)= -11.791,p < 0.01),正确率在低负荷条件下显著大于高负荷条件(92.26/87.37,t(15)=3.05,p < 0.05). 故知上述两种驾驶任务设置,实现了驾驶员脑力负荷的差异.
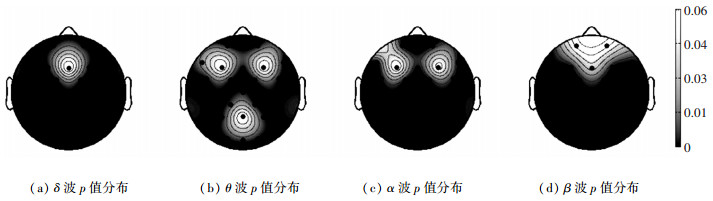
步骤3 特征指标构建和选取.基于2.1节的处理方法对脑电信号进行分段处理并做快速傅里叶变换,按2.2所述方法得出 δ、θ、α和β 4个指标在32个电极上个高低负荷数据间的p值,其脑地形图如图 4所示.
|
图 4 p值脑地形 |
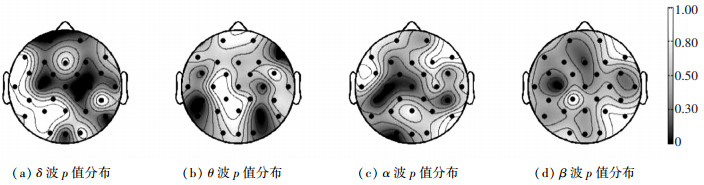
为能直观看出 p值大小顺序,将所有p值进行由小到大排序,将0~1均匀分为128个值,按p 值顺序置入电极位置,作出直观脑地形图如图 5所示.
|
图 5 p值排序脑地形 |
由此选出效果最好的10个指标,构成驾驶脑力负荷的识别特征向量.
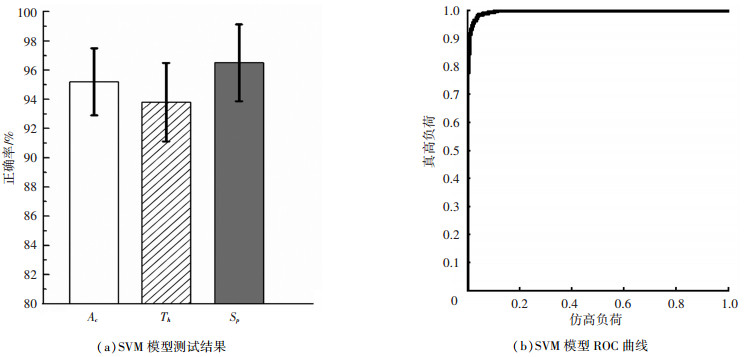
步骤4 脑力负荷识别.随机抽取12名被试的脑电数据作为训练样本,余下4名被试的脑电数据作为测试样本.对SVM模型予以训练和测试,其结果如图 6所示.
|
图 6 SVM测试效果 |
由图 6(a)可知识别模型的判断正确率较好,模型识别正确率可达93.8%~96.5%,平均正确率为95.2%. 图 6(b)ROC曲线图反应出识别模型对于数据的分类具有较好的稳定性.
6 结论1) 针对驾驶员脑力负荷识别问题,基于脑电信号指标构建了一种驾驶员脑力负荷识别方法,通过研究,进一步验证了频域指标不仅可以对认知实验类的脑力负荷进行识别,也可对模拟环境下驾驶员的脑力负荷进行有效识别.
2) 基于非参数的Kruskal-Wallis检验,提出了一种通过对比不同等级下脑电指标分布的差异性,选取脑力负荷识别特征指标的方法.
3) 采用脑电信号的频谱特征指标,结合SVM模型,构建了一种驾驶员脑力负荷识别模型,实验结果表明该模型具有较高的识别率.
| [1] |
白玉, 何熊, 龙力. 手机使用对驾驶员行为影响研究综述[J]. 交通信息与安全, 2013(3): 136-142. |
| [2] |
李丽, 袁玫. 使用车载导航系统下驾驶员脑力负荷影响因素分析[J]. 安全与环境学报, 2011(6): 202-204. |
| [3] |
程杰, 唐智慧, 李小玲, 等. 驾驶中听音乐对驾驶安全的影响[J]. 中国安全科学学报, 2014(5): 21-25. |
| [4] |
王培, 饶培伦. 驾驶员对北京市道路交通标志的感知和理解[J]. 工业工程, 2011, 14(1): 114-117. |
| [5] |
张诗卉. 城市典型路口驾驶员脑力负荷分析与实验验证[D]. 北京: 清华大学, 2010. http://cdmd.cnki.com.cn/Article/CDMD-10003-1011280887.htm
|
| [6] |
杨家忠, 张侃. 交通复杂度因素对空中交通管制员脑力负荷与情境意识的影响[J]. 心理科学, 2010(2): 368-371. |
| [7] |
陈阳. 城市道路环境中驾驶员工作负荷试验研究[D]. 西安: 长安大学, 2009. http://cdmd.cnki.com.cn/Article/CDMD-11941-2009219888.htm
|
| [8] |
HAGA S, SHINODA H, KOKUBUN M. Effects of task difficulty and time-on-task on mental workload[J]. Japanese Psychological Research, 2002, 44(3): 134-143. DOI:10.1111/jpr.2002.44.issue-3 |
| [9] |
SZALMA J L, WARM J S, MATTHEWS G, et al. Effects of sensory modality and task duration on performance, workload, and stress in sustained attention[J]. Human Factors:The Journal of the Human Factors and Ergonomics Society, 2004, 46(2): 219-233. DOI:10.1518/hfes.46.2.219.37334 |
| [10] |
肖元梅, 王治明, 王绵珍, 等. 主观负荷评估技术和NASA任务负荷指数量表的信度与效度评价[J]. 中华劳动卫生职业病杂志, 2005(3): 178-181. |
| [11] |
VENABLES L, FAIRCLOUGH S H. The influence of performance feedback on goal-setting and mental effort regulation[J]. Motivation and Emotion, 2009, 33(1): 63-74. DOI:10.1007/s11031-008-9116-y |
| [12] |
PFURTSCHELLER G, BRUNNER C, SCHLOGL A, et al. Mu rhythm (de) synchronization and EEG single-trial classification of different motor imagery tasks[J]. Neuroimage, 2006, 31(1): 153-159. DOI:10.1016/j.neuroimage.2005.12.003 |
| [13] |
GRIER R A, WARM J S, DEMBER W N, et al. The vigilance decrement reflects limitations in effortful attention, not mindlessness[J]. Human Factors:The Journal of the Human Factors and Ergonomics Society, 2003, 45(3): 349-359. DOI:10.1518/hfes.45.3.349.27253 |
| [14] |
张晓龙, 江川, 骆名剑. ROC分析技术在机器学习中的应用[J]. 计算机工程与应用, 2007, 43(4): 243-248. |
| [15] |
CHRYSLER S, PARK E S, NELSON A, et al. Driver workload at higher speeds[R]. College Station: Texas Transportation Institute, Texas A&M University System, 2010.
|
 2016, Vol. 48
2016, Vol. 48


