近年来,随着中国西部交通路网迅速发展,西部地区涌现出大量的公路交通线.为了跨越这些地形复杂、山高谷深,沟壑纵横的地区,高墩大跨度非规则桥梁结构被广泛运用(其中以公路三跨连续刚构桥较为常见),其跨度与桥墩高度往往较大,各桥墩之间的高差也相差很大,有时可达三、四十米.而西部地区地震带分布广泛,地震活动频繁,很多桥梁正处于地震频发区和高烈度区域,近场地震常造成桥梁结构极其普遍和严重的破坏[1],这使得桥梁结构的运营安全受到巨大的挑战.而目前在中国公路桥梁抗震规范中,对于墩高大于40 m的桥梁,并没有较为合理有效的抗震评估方法[2].
随着各国抗震理论的不断发展,地震易损性分析方法已成为评估桥梁结构抗震性能的重要手段,它反映了特定强度地震作用下结构反应超过规定破坏极限状态的概率,一般采用经验统计和数值模拟这两种途径获得[3].由于缺乏具体震害资料,近些年来,国内外学者对数值模拟分析法的易损性模型进行了更加广泛和系统的研究. Mackie等[4]针对美国典型公路三跨连续梁桥进行了远场地震易损性研究;吴文朋等[5]基于IDA(incremental dynamic analysis)分析法对规则连续刚构桥进行了远场地震易损性分析;Danusa等[6]对加拿大5种常见类型桥梁进行了远场地震易损性分析;Billah等[7]对美国加州典型π型桥墩开展了近、远场地震易损性分析.但以上大部分易损性研究工作仅针对常见规则桥梁(如简支梁、中小跨度连续梁等)及单个桥梁构件(如桥墩、支座等)进行的,且大部分学者主要研究远场地震易损性,而对于像西部地区高墩大跨连续刚构这类非规则桥梁结构在近场地震作用下的易损性研究较少,因此急需开展高墩、大跨非规则桥梁结构近、远场地震易损性分析工作,深入研究近、远场地震作用下非规则桥梁的抗震性能(下文中所研究的“非规则桥梁”仅代表高墩、大跨非规则连续刚构这类桥型).
基于此,本文以一座西部地区典型高墩大跨非规则连续刚构桥作为研究对象,考虑地震动和结构参数的不确定性,采用概率性地震需求分析方法,建立这类桥梁在近、远场地震作用下的易损性曲线,对比分析近、远场桥梁的地震易损性特点,评估这类桥梁结构的抗震性能,为该类桥梁在近场高震区的设计及震后损伤识别等提供依据.
1 地震易损性分析方法 1.1 概率地震需求模型概率地震需求模型描述的是结构地震需求参数与地震动强度指标之间的关系,基于结构动力时程分析结果,利用该模型便可获得桥梁结构易损性曲线. C. Allin等[8]在假设结构地震需求参数E服从对数正态分布的前提下,利用回归分析研究了地震需求中位数E与地震动强度参数M之间的关系,结果表明两者满足指数关系,即
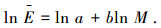
|
(1) |
式中a和b为未知系数,通过回归分析求解得到.由于结构在每种地震动强度下对应唯一的结构需求,则结构地震需求的离散度βE|M为
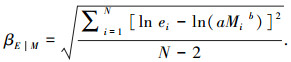
|
(2) |
式中:ei为桥梁结构在第i个地震作用下的地震需求峰值;Mi为第i个地震动强度峰值;N为地震动的总数.
基于回归分析确定对数正态分布参数后,概率性地震需求模型即可表示为

|
(3) |
式中:μ=(ln e-ln a)·b-1为在给定地震需求条件下,其对应地震动强度中位数的自然对数值;ξ=βE|M·b-1为对数标准差.
1.2 构件地震易损性分析基于上述概率地震需求模型,便可建立地震易损性曲线,对桥梁结构进行地震易损性分析.桥梁构件地震易损性可定义为在特定地震动强度作用下,桥梁构件的抗震需求达到或超越其自身实际抗震能力的概率,当假设构件的抗震能力和需求服从对数正态分布时,其计算公式为
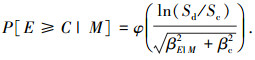
|
(4) |
式中:βc为桥梁构件抗震能力对数标准差;φ(·)为标准正态累计分布函数;Sc为某种极限状态结构抗震能力的中位数;Sd为结构地震需求中位数.
2 工程实例 2.1 工程概况及有限元模型以西部地区某非规则连续刚构桥为例,研究了这类非规则桥梁的地震易损性.该桥位于Ⅱ类场地,其上部结构为三跨变截面连续箱梁,桥跨布置为(125+220+125)m,采用C60混凝土;2#、3#主墩采用相同截面形式的矩形空心墩,两侧交接墩采用双柱薄壁空心墩,桥墩为C40混凝土,1#~4#墩墩高分别为67.45、102.0、99.5、85.42 m,如图 1所示;桥墩纵向配筋率为1.2%,配箍率为0.75%,纵筋和箍筋均采用HRB335级;在1#、4#墩安装了GPZ10SX±200双向活动盆式支座,抗震设防类别为A类.

|
图 1 桥梁结构概况示意图(cm) |
采用OpenSees软件建立了全桥有限元模型.主梁采用弹性梁单元模拟,考虑自重和二期恒载.盆式支座按照《公路桥梁抗震设计细则》[9]6.3.7节建议的方法采用双线性理想弹塑性弹簧单元模拟.桥墩采用弹塑性纤维单元模拟,单元中钢筋和混凝土材料被赋予了相应的本构关系,其中混凝土的本构关系由Kent-Scott-Park模型确定;钢筋本构关系由Giuffre-Menegotto-Pinto模型确定,两种材料的本构参数计算方法详见文献[10].
2.2 不确定性 2.2.1 地震动的不确定性目前工程界常按断层距大小来划分近、远场地震,即断层距不超过某一限值的地震动为近场地震动,反之为远场地震动.但断层距限值仍未统一,不同学者有不同观点,总的来说限值都定义在20~60 km这个范围[11],具体的取值要结合震级和地震影响.
根据桥梁所处场地类型,以公路桥梁抗震设计细则[9]中的设计反应谱为目标谱,参考Luco[12]的分析方法,从太平洋地震工程研究中心的“强地面运动数据库”选出了土层平均剪切波速在250 m/s<v<500 m/s,并以断层距R= 30 km为分界点的近场和远场地震动各100条,其峰值加速度PGA(peak ground acceleration)覆盖范围为0.1g~1.0g.按照这个筛选原则,本文选取的地面运动记录可分为两组:1)近场地震动,断层距R≤ 30 km;2)远场地震动,断层距R> 30 km.
本文主要研究结构纵桥向的地震易损性.其中选取的近场地震动类型较为丰富,包含有走滑断层地震动(1999年土耳其Kocaeli地震),倾滑断层地震动(1999年台湾集集地震、1994年美国Northridge地震)等类型.选出的地震能够充分体现近场地震动高能量脉冲运动的特征,并包含有方向性效应、长周期速度脉冲效应、上盘效应及滑冲效应等. 图 2给出了从Kocaeli地震中选取的某条近场地震动记录[13](震中距2.6 km,台站名称KOCAELI/YPT330),该地震动记录包含了明显的双向速度脉冲现象,这种速度脉冲是断层上大多数地震辐射的累计效果.

|
图 2 Kocaeli地震KOCAELI/YPT台站地震动记录结果 |
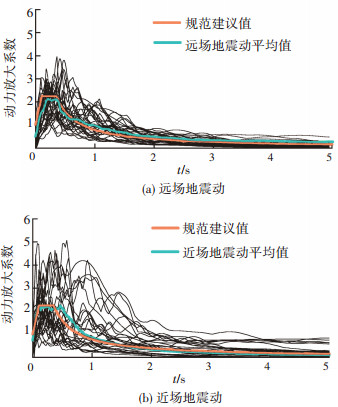
近、远场地震动的动力放大系数β谱如图 3所示,图中还给出了近、远场动力放大系数均值和规范建议取值.由图可知一些地震动的动力放大系数峰值远高于规范反应谱中建议的β= 2.25的数值[9],并且两组地震动的动力放大系数的离散性也比较大,但两组地震动的动力放大系数均值总体来说与规范建议值还是比较接近.
|
图 3 地震波动力放大系数β谱(ξ=0.05) |
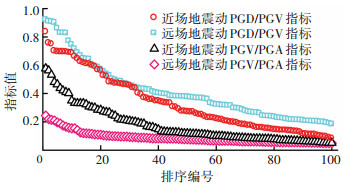
对比近、远场β谱均值曲线可知,远场地震动的β谱峰值敏感区[14]比较集中,而近场地震动的β谱峰值敏感区较宽,且下降较缓慢,为进一步了解所选地震动的特征,图 4给出了两组地震动PGV/PGA和PGD/PGV指标比值分布图(图中将指标比值由大到小进行排序,PGV(peak ground velocity)为地震动峰值速度,PGD(peak ground displacement)为地震动峰值位移),由图可知近场地震动PGV/PGA比值比远场地震动比值偏高,这说明近场地震动低频分量丰富、特征周期较长.而近场地震动PGD/PGV比值比远场地震动略低,这表明近场地震动位移敏感区会较早出现.
|
图 4 近、远场地震动指标值分布 |
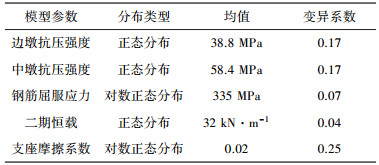
对于非规则桥梁而言,其材料特性及荷载效应的不确定性将直接影响桥梁自身的抗震性能,因此在易损性分析时需考虑上述因素的影响.针对非规则连续刚构桥的结构特点,并结合汶川地震桥梁震害调查资料及以往研究成果[10],本文确定了易损性分析中的不确定性参数及其分布特征参数,见表 1.
| 表 1 不确定性参数及其分布特征参数表 |
利用随机抽样方法建立地震动-桥梁分析样本库,运用OpenSees软件对各地震-桥梁样本进行动力时程分析,基于分析结果进行结构概率地震需求分析,具体流程如下:1)根据2.2节所确定的不确定性参数,采用拉丁超立方体方法[10]进行抽样填充得到这些参数样本,并建立桥梁样本库.鉴于计算规模和所选用的抽样方法,本文建立100个桥梁分析样本. 2)根据国内外学者已有的研究成果[3, 5, 10, 15],本文将结构破坏等级分为轻微损伤、中等损伤、严重损伤和完全破坏4种状态,并确定了非规则桥梁的地震危险构件及构件损伤指标,具体包含:近、远场1#桥墩墩底曲率φ1-B和φ1-B′;近、远场2#墩墩顶曲率φ2-T和φ2-T′;近、远场2#墩墩底曲率φ2-B和φ2-B′;近、远场3#桥墩墩顶曲率φ3-T和φ3-T′;近、远场3#桥墩墩底曲率φ3-B和φ3-B′;近、远场4#墩墩底曲率φ4-B和φ4-B′;近、远场1#墩支座相位移Δ1-Z和Δ1-Z′、近、远场4#墩支座相对位移Δ4-Z和Δ4-Z′. 3)将近、远场各100组地震动样本和100个桥梁样本一一配对,建立近、远场地震动-桥梁分析样本库,然后进行动力时程分析,并获得各构件的最大动力响应. 4)确定构件最大动力响应和对应地震动强度峰值,在对数空间中绘制其散点图并进行回归分析,计算得到式(1)中的a、b和式(2)中的βE|M值.
根据上述分析流程对桥梁各构件进行概率地震需求分析,便可确定各构件地震需求与地震动强度之间的关系式.
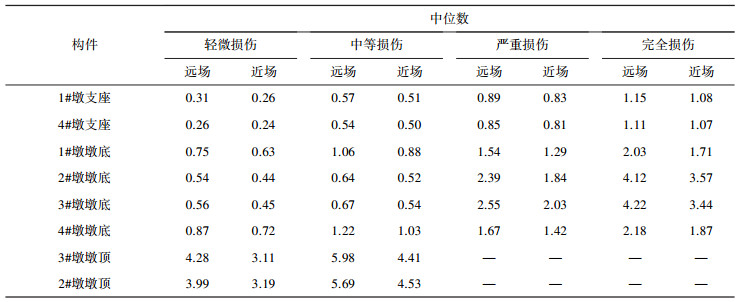
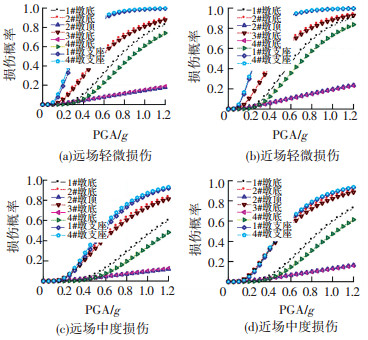
2.4 桥梁结构地震易损性分析 2.4.1 桥梁构件易损性分析基于2.3节的分析结果,利用式(4)便可得到近、远场地震作用下各构件在4种损伤状态下的地震易损性曲线,见图 5.由图 5可知在近、远场地震作用下不同构件的易损性曲线有类似的形状,但不同的损伤状态具有不同的损伤概率.由各构件的易损性曲线可知,1#、4#边墩支座最容易发生损伤,而2#、3#中墩墩顶截面最不容易发生损伤.为比较各构件易损性具体情况,采用超越概率地震动强度指标中位数来描述构件的易损性,即某一损伤状态下中位数越小构件越容易发生损伤破坏,各构件在近、远场地震作用下4种损伤状态所对应地震动强度指标中位数见表 2.
|
图 5 桥梁构件近、远场地震易损性曲线 |
| 表 2 桥梁构件近、远场地震易损性参数 |
由表 2可知,在近、远场地震作用下,对于轻微和中等损伤状态,4#边墩支座最容易发生损伤,其次是1#边墩支座、2#墩底截面、3#墩底截面、1#墩底截面、4#墩底截面、2和3#墩顶截面.
对于严重和完全损伤状态,2#、3#桥墩墩顶截面几乎不会发生这两种损伤.而两边墩支座依然最容易发生损伤,其次是两边墩墩底截面、两中墩墩底截面,此时各墩底截面易损情况与轻微和中等损伤结果略有不同.
综上所述,因非规则连续刚构桥各墩高差较大,使得在地震作用下桥梁各构件的易损性存在差异.这种差异一方面表现在各桥墩或支座在相同损伤状态下损伤破坏概率各不相同,另一方面不同损伤状态对应的桥梁构件易损分布规律也不尽相同.因此开展非规则桥梁地震易损性分析,深入研究其抗震性能是非常必要的.
此外,近、远场地震易损性曲线有类似的形状,但同一构件在两种地震动作用下的损伤概率却存在一定的差异,因此需要对近、远场地震作用下桥梁结构易损性的特点及差异进行深入研究.
2.4.2 近、远场地震易损性对比分析为研究非规则桥梁各构件近、远场地震易损性的差异,将相同构件的易损性曲线绘于同一图形中,并对比分析两种地震易损性的不同,图 6给出了4种构件在轻微损伤状态下对应的近、远场易损性曲线.

|
图 6 各构件近、远场地震易损性曲线对比 |
由图 6可知,4种构件在轻微损伤状态下,其近、远场易损性曲线存在一定的偏差,且近场易损性大于远场.不同构件的损伤概率偏差程度和出现偏差范围均不相同,如:1#墩墩底损伤概率偏差范围为0.2g~1.2g;4#边墩支座偏差范围为0.1g~0.8g.
由上述分析可知,对于非规则连续刚构桥各危险截面和支座,在相同PGA条件下,近场地震损伤概率比远场地震损伤概率大,且两者的偏差情况与结构部位、损伤状态密切相关.
为进一步分析桥梁结构近、远场地震易损性差异的具体特征,图 7给出了部分构件近、远场损伤概率偏差与PGA的关系曲线.
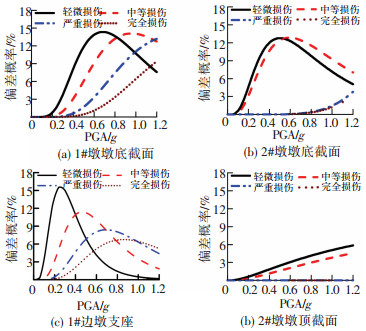
|
图 7 各构件近、远场地震损伤概率偏差趋势 |
由图 7可知,对于1#、2#墩墩底截面,在轻微和中等损伤状态下,其近、远场损伤概率偏差变化趋势相近,均为先增加后减小,最大偏差值在13%~14%之间.而对于严重和完全破坏状态,两种截面近、远场损伤概率偏差均随着PGA的增加而增加.
对于边墩支座,4种损伤状态下,近、远场损伤概率偏差值的变化趋势均为先增加后减小,但各损伤状态最大偏差所对应的PGA值各不相同,最大偏差概率达到15.6%.
对于中墩墩顶截面,在轻微和中等损伤状态下,概率偏差随着PGA的增大而缓慢增大.严重和完全破坏对应的偏差几乎为零.
综上可知,对于非规则连续刚构桥,其结构构件在近、远场地震作用下发生损伤破坏的概率存在明显的差异,最大损伤概率偏差可达15.6%,其损伤概率偏差大小和偏差变化趋势与结构部位、损伤状态密切相关.
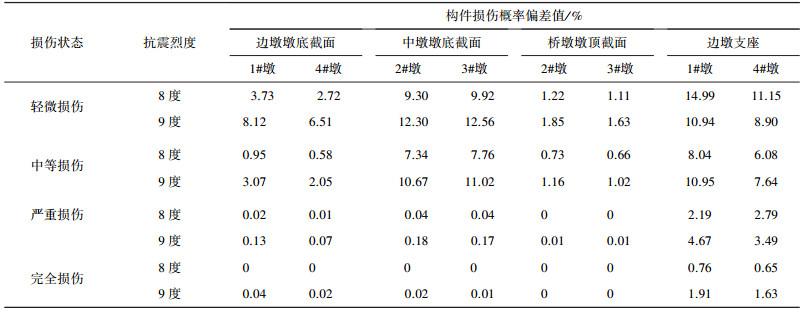
在实际工程中,人们往往关注桥梁结构的抗震设防等级,根据《公路桥梁抗震设计细则》[9]第3.1.4节可知,各类公路桥梁采用抗震烈度作为桥梁的抗震设防标准,以此确定桥梁结构的抗震设防等级,而抗震设防烈度与地震动峰值加速度存在对应关系.因此,本文重点关注桥梁结构抗震等级,即桥梁在特定PGA下的抗震性能,也就是重点关注地震损伤概率.基于此,本文结合规范[9]与上述近、远场地震易损性研究成果,对比研究近、远场地震作用下桥梁结构在抗震设防烈度8度(0.3g)和9度(0.4g)时的损伤概率差异性. 表 3给出了两种抗震设防烈度下各构件近、远场损伤概率偏差数据.
| 表 3 桥梁构件近、远场地震损伤概率偏差数据表 |
为了研究桥梁各构件偏差的相互关系,利用表 4中数据对各构件偏差值进行了相关性分析(图 8),分析结果表明,两边墩墩底截面的相关系数达到0.93以上,两中墩墩底截面相关系数均大于0.97,两墩顶截面的相关系数均为1,两支座的相关系数达到0.94以上,因此可以分别研究墩顶截面、边墩墩底截面、中墩墩底截面、支座4种类型构件的损伤概率偏差值特征.

|
图 8 各构件损伤概率偏差值相关系分析云图 |
由表 3可知,对于2#、3#中墩底截面,综合考虑轻微损伤和中等损伤情况,在0.3g时近、远场损伤概率偏差在7%~10%,0.4g损伤偏差在10%~13%,此时两种损伤状态对应的偏差均值分别为12.43%和10.58%,这表明0.2g~0.3g近场地震作用下,中墩墩底截面的损伤概率要比远场地震作用的损伤概率高出10%~13%.
对于边墩墩底截面,综合考虑轻微损伤和中等损伤,各边墩损伤概率偏差在2%~8%之间.而对于支座,轻微损伤状态下损伤概率偏差在10%~13%之间,中等损伤偏差在8%左右,严重损伤概率偏差在3%左右.
由上述分析可知在抗震设防烈度8度(0.3g)和9度(0.4g)条件下,近场地震作用对非规则桥梁各构件的破坏概率比远场地震要高,不同构件其损伤概率偏差大小不同,整体看来偏差最大发生在边墩支座,其次是中墩墩底截面.偏差较大的损伤状态为轻微和中等损伤状态.
综上所述,对于高墩大跨非规则连续刚构桥,在近场地震作用下其地震损伤概率比远场地震损伤概率更大,且不同构件具有不同的易损性特征.结合图 3、4、7可知,导致上述结果的主要原因是近、远场地震动频谱特性存在明显的差异以及桥梁自身的非规则性.对于近场地震动,其PGV/PGA比值相比于远场地震动更大,这促使近场地震动反应谱产生较宽的加速度敏感区,而对于大跨高墩桥梁结构,其结构周期较长,由于近场地震动加速度敏感区较宽,导致大跨高墩桥梁结构越来越多的振型处于该区域内,使得近场地震动激励下的结构响应会显著增大.此外由于所选取的近场地震动PGD/PGV比值较小,其位移敏感区会较早出现,且选取近场地震动包含有明显的速度脉冲等现象,这使得长周期的大跨高墩非规则桥梁结构进入位移敏感区后将造成更大的位移冲击,即非规则桥梁在近场地震动作用下需要更大的强度来保持结构的安全,另一方面,由于桥梁各墩高差较大,使得各构件的地震响应更为复杂,结构的抗震需求与常规桥梁相比更加难以确定.因此进一步深入研究不同结构参数(墩高、跨度等参数)的桥梁地震易损性分布规律是今后解决高墩大跨非规则桥梁结构抗震问题的重要途径.
3 结论1) 对于非规则连续刚构桥,在近、远场地震作用下各构件地震易损性较大,轻微损伤对应的各构件PGA中位数变化范围在0.26g~3.99g之间,中等损伤对应的PGA中位数变化在0.51g~5.69g之间,严重损伤和完全破坏对应的PGA中位数变化范围更大.
2) 依据非规则连续刚构桥各构件近、远场易损性分析结果可知,边墩支座最容易发生损伤破坏.而对于各墩底截面,2#墩墩底截面最容易发生轻微和中等破坏,1#墩墩底截面最容易发生严重和完全破坏.
3) 非规则连续刚构桥各构件近、远场易损性对比分析表明:桥梁结构近场地震损伤概率比远场要大,且构件近、远场地震损伤概率存在一定偏差,支座最大损伤概率偏差可达15.6%,边墩墩底截面最大偏差可达14.2%.各构件损伤概率偏差大小和偏差变化趋势与结构部位、损伤状态密切相关.
4) 在抗震设防烈度8度或9度条件下,对各构件近、远场地震易损性偏差分析表明:在轻微和中等损伤状态下,边墩支座近、远场损伤概率偏差在7.0%~13.0%之间;各中墩墩底截面近、远场损伤偏差在7.5%~11.0%之间,因此研究非规则桥梁近场地震易损性及其抗震性能至关重要.
5) 近、远场地震动频谱特性的差异及桥梁结构自身的非规则性导致了高墩大跨连续刚构桥近、远场地震易损性的不同,桥梁结构地震易损性的大小与地震动的PGV/PGA比值、PGD/PGV比值、加速度敏感区宽度及断层距等因素密切相关.
| [1] |
胡聿贤. 地震工程学[M]. 2版. 北京: 地震出版社, 2006.
|
| [2] |
李建中, 宋晓东, 范立础. 桥梁高墩位移延性能力的探讨[J]. 地震工程与工程振动, 2005, 25(1): 43-48. |
| [3] |
NIELSON B G. Analytical fragility curves for highway bridges in moderate seismic zones[D]. Atlanta: GA Georgia Institute of Technology, 2005. https://smartech.gatech.edu/bitstream/handle/1853/7542/nielson_bryant_g_200512_phd.pdf
|
| [4] |
MACKIE K R, STOJADINOVIC B. Post-earthquake functionality of highway overpass bridges[J]. Earthquake Engineering & Structural Dynamics, 2006, 35(1): 77-93. |
| [5] |
吴文朋, 李立峰. 基于IDA的高墩大跨桥梁地震易损性分析[J]. 地震工程与工程振动, 2012(3): 117-123. |
| [6] |
DANUSAH T, JAMIE E P, PATRICK P. Fragility curves of typical as-built highway bridges in eastern Canada[J]. Engineering Structures, 2012, 40: 107-118. DOI:10.1016/j.engstruct.2012.02.019 |
| [7] |
BILLAHA M, ALAM S, BHUIYAN M A R. Fragility analysis of retrofitted multicolumn bridge bent subjected to near-fault and far-field ground motion[J]. Journal of Bridge Engineering, 2013, 18(10): 992-1004. DOI:10.1061/(ASCE)BE.1943-5592.0000452 |
| [8] |
CORNELLC A, JALAYER F, HAMBURGER R O, et al. Probabilistic basis for 2000 SAC federal emergency management agency steel moment frame guidelines[J]. Journal of Structural Engineering, 2002, 128(4): 526-533. DOI:10.1061/(ASCE)0733-9445(2002)128:4(526) |
| [9] |
重庆交通科研设计院. 公路桥梁抗震设计细则: JTG/T B02-01-2008[S]. 北京: 人民交通出版社, 2008.
|
| [10] |
陈力波. 汶川地区公路桥梁地震易损性分析研究[D]. 成都: 西南交通大学, 2012. http://cdmd.cnki.com.cn/Article/CDMD-10613-1014251544.htm
|
| [11] |
STEWART J P, CHIOU S J, BRAY J D, et al. Ground motion evaluation procedures for performance-based design: report No. 01-09: 63-67[R]. Berkeley, California: Pacific Earthquake Research Centre, 2002. https://www.sciencedirect.com/science/article/pii/S0267726102000970
|
| [12] |
LUCO N. Probabilistic seismic demand analysis, SMRF connection fractures, and near source effects[D]. Palo Alto, California: Stanford University, 2002.
|
| [13] |
美国太平洋地震工程研究中心. 关于土耳其Kocaeli地震动实测加速度数据[DB/OL]. (2005-09-20)[2014-10-4]. http://peer.berkeley.edu/svbin/Detail?id=P1114.
|
| [14] |
张林春. 大跨度刚构桥近场脉冲型地震动反应分析[D]. 哈尔滨: 哈尔滨工业大学, 2007. http://cdmd.cnki.com.cn/Article/CDMD-10213-2008193543.htm
|
| [15] |
董俊, 单德山, 张二华, 等. 非规则连续刚构桥地震易损性分析[J]. 西南交通大学学报, 2015, 50(5): 635-642. |
 2016, Vol. 48
2016, Vol. 48