哈尔滨工业大学学报  2016, Vol. 48 Issue (3): 171-177  DOI: 10.11918/j.issn.0367-6234.2016.03.029
0

引用本文 

于天剑, 陈特放, 邓江明, 陈雅婷, 成庶. 磁浮直线电机的等效控制模型改进[J]. 哈尔滨工业大学学报, 2016, 48(3): 171-177. DOI: 10.11918/j.issn.0367-6234.2016.03.029.
YU Tianjian, CHEN Tefang, DENG Jiangming, CHEN Yating, CHENG Shu. The improvement of equivalent control model research on the maglev linear motor[J]. Journal of Harbin Institute of Technology, 2016, 48(3): 171-177. DOI: 10.11918/j.issn.0367-6234.2016.03.029.

基金项目

国家自然科学基金（61273158）

作者简介

于天剑(1988-), 男, 博士研究生;
陈特放(1957-), 男, 教授, 博士生导师

通信作者

成庶, 6409020@qq.com

文章历史

收稿日期: 2014-12-26
Abstract              Full text              Figures/Tables              PDF
磁浮直线电机的等效控制模型改进
于天剑, 陈特放, 邓江明, 陈雅婷, 成庶     
中南大学 交通运输学院, 410075 长沙
收稿日期: 2014-12-26
基金项目: 国家自然科学基金（61273158）
作者简介: 于天剑(1988-), 男, 博士研究生;
陈特放(1957-), 男, 教授, 博士生导师
通信作者: 成庶, 6409020@qq.com
摘要: 为准确测量电机参数，提出一种新的改进的SLIM等效电路参数辨识方法，利用不同频率时的电机推力、变频器输出电压和电流等静态堵转特性，结合算法推算出适合控制用的SLIM等效电路中的初级电阻、漏感、次级等效电阻和漏感参数.通过MATLAB仿真实验，结果表明各动态参数幅值的修正对提高电机速度辨识精度是有利的，并在中低速磁悬浮模拟实验平台上进行实验，验证了在改进后的T-模型下，对结果分析可以得知电机的状态辨识效果和精度得到了提高，并对以后的电机参数设计具有指导意义.
关键词: SLIM     等效电路     参数设计     MATLAB仿真     磁悬浮实验平台    
The improvement of equivalent control model research on the maglev linear motor
YU Tianjian, CHEN Tefang, DENG Jiangming, CHEN Yating, CHENG Shu     
School of Traffic and Transportation Engineering, Central South University, 410075 Changsha, China
Abstract: In order to measure the motor parameters. This paper presents a new and improved SLIM equivalent circuit parameter identification, the motor thrust using different frequencies, the inverter output voltage and current, static stall characteristics, combined with suitable control algorithms calculate the equivalent circuit of SLIM primary resistance, leakage in ductance, secondary equivalent resistance and leakage inductance parameter. By finite element simulation experiments show that the amplitude of the dynamic parameters of each amendment to increase the motor speed identification accuracy is beneficial, conduct experiments on low-speed maglev simulation platform, validated under T-improved model, the motor status identification results show the current state of reconstruction, not only in the dynamic process of change or steady-state accuracy, and has a guiding significance to the future design of motor parameters.
Keywords: SLIM     equivalent circuit     parametric design     MATLAB simulation     levitation experiment platform    

目前中低速磁悬浮的驱动系统普遍采用单边短初级长次级直线感应电机，电机运行时，初、次级保持一定的机械间隙，其速度检测也不同于旋转式电机，现有的速度检测方法有雷达定位[1]、计量轨枕和交叉感应回线[2]等，这些方法都必须铺设专门的检测和支撑设备，测速成本高、维护麻烦，因设备故障或外部干扰导致电机控制失败时有发生[3-4].因此研究单边直线感应电机(SLIM)的无速度传感器控制很有价值，目前针对SLIM的研究主要集中在等效电路参数、边端效应补偿及推力法向力特性等方面[5-6]，文献[4]提出一种采用BP神经网络的SLIM速度估算方法，但网络训练样本获取复杂且无法满足电机的动态控制要求；文献[7]研究了直线感应电机的无速度传感器直接磁场定向控制并未针对SLIM特有的边端效应进行有关参数补偿，当互感参数减小时，估算偏差较大.在本文中讨论了SLIM在实际运行工况下的横、纵向动态端部效应和“集肤”效应对电机气隙磁场的影响，将分析得到的结果统一到对电机T-模型的改进上，并导入与电机几何尺寸、次级导体材料、和滑差率有关的4个改进系数.利用改进的SLIM T-模型，可以修正计算与观测器设计有关的各动态参数.通过在中低速磁悬浮模拟实验平台上进行的两个方面的实验, 验证了采用改进后的T-ECM，电机的辨识速度在动态响应过程和稳态精度方面都能获得满意的性能.

1 电机等效模型改进过程分析

依据麦克斯韦(Maxwell)电磁场方程组[8-9]可得电流层函数为

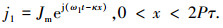
式中：κ=π/τ，ω1为初级电流层的频率，P为极对数，τ为极距.可得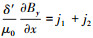

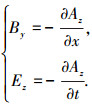
式中 δ′ 为电磁气隙，即 δ′=kδkμδ，δ为初次级铁芯表面之间的距离，j1、j2分别为初级和次级的线电流密度矢量.因为电流被假设成无限薄，只有z分量，故矢量磁位A也只有z分量，Az为磁位的z分量，Ez为电场强度的z分量，By为气隙中磁通密度的y分量. 可得

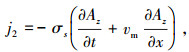
其中：σs次级电导率，σs =σd，σ次级导体体积电导率，d导体厚度；次级导体沿着坐标x的移动速度为vm.可进一步得到

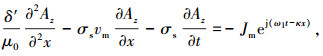
(1)

因为初级电流按照周期 ejωt 随着时间 t 变化，可进一步设矢量磁位

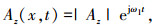
(2)

将式(2)代入式(1)，求得全解为

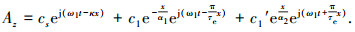
(3)

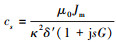
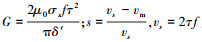
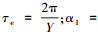
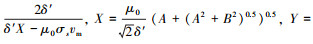
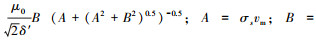
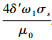
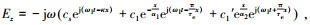
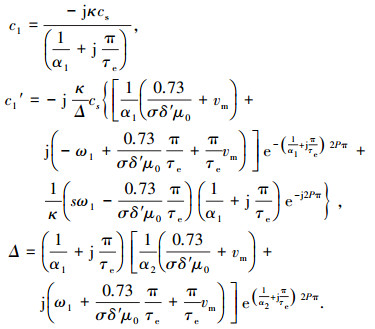
式中：c1 、c1′ 为待确定系数常量；而式(3)中各个系数符号为；G为电机的品质因数，为磁场同步速度，f为初级绕组注入的电流频率；. 联立各式可求得 其中待定系数 c1、c1′，可根据边界上电场强度切线分量相等的原则求得.

 1.1 考虑纵向动态端部效应的有关参数改进

气隙感应电场强度 z 分量的计算公式[10]为

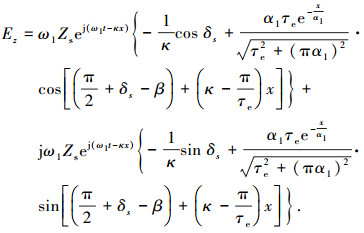
因为传到次级和气隙的视在功率 S2-3为S2－3= 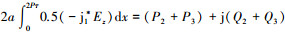，由于P3以及次级的Q2均为0，因此只计传递到次级的有功和气隙无功能量S2－3=P2+jQ3.

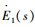
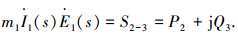
若设初级平衡气隙相电势有效值为，根据复量功率传递相等的原则，有

其中初级电流层的幅值与初级相电流有效值的关系为.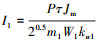

再设 R2(s)和Xm(s)为计及纵向端部效应时的归于初级的次级相电阻和初级每相磁化电抗，于是，结合各式可得

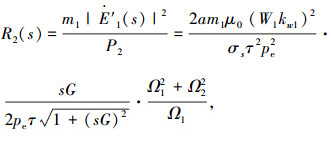
(4)
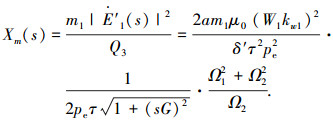
(5)

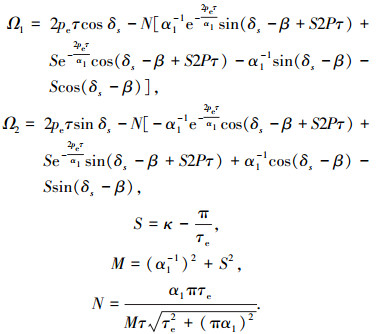
其中 pe 为两端为“半填充槽”的等值极对数，pe= 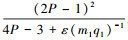，若忽略“半填充槽”的影响，有 pe=P；ε=L/2－Pτ(L为电机铁心总长，ε非绕组覆盖区域)；m1为初级相数，q1 为初级每极每相串联匝数.

令 Kr(s)和Kx(s)分别为次级相电阻和初级每相磁化电抗的纵向端部效应改进系数，由式(4)、(5)可得考虑纵向动态端部效应的直线感应电动机等效电路动态参数改进如下.

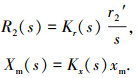
式中相关系数 Kr(s)和Kx(s)的详细表达为

1.2 考虑第2种横向端部效应的有关参数改进

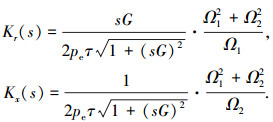
设每极磁通为 φ(t)，则根据直线电机的边界结构，有

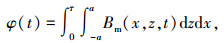
(6)

其中

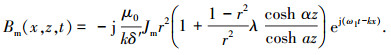
求解式(6)可得

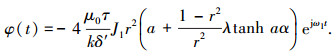
(7)

由于初级每相磁势的瞬时值为

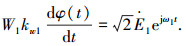
(8)

由式(7)、(8)可得

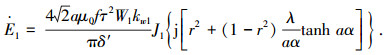
类似的，考虑到式中的场复量功率相等的原则, 有

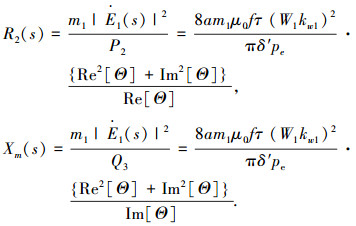
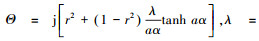
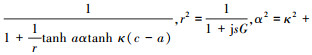
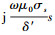
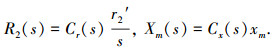
式中：，而a、c分别为初级铁芯和次级导体宽度的二分之一再设Cr(s)和Cx(s)为次级相电阻和初级每相磁化电抗的第2种横向端部效应改进系数，故可得

式中各相关系数：

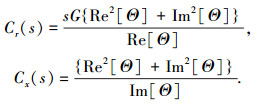
各参数是由场路复量功率相等的关系直接计算出来的，故所有计算结果延续了电磁场分析的严谨性.

1.3 考虑集肤效应的影响

设 kf为“集肤”效应系数[11]，由文献[11]直接给出其计算公式：

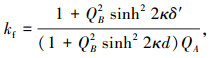
式中：

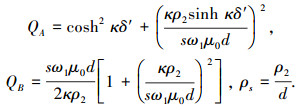
可知

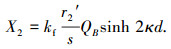
系数kf反映了“集肤”效应对次级电阻的影响，考虑初级电阻R1和初级漏抗X1，初级每相电阻为

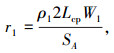
式中：Lcp 为绕组半匝平均长，Lcp=2a+Le，Le 为初级绕组端部长 Le=1.4τ，SA 为导向截面积.

初级每相总漏抗为

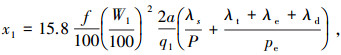
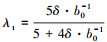
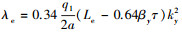
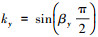
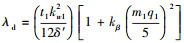
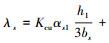
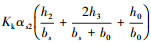
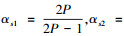
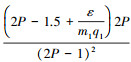
式中：λt 为齿端漏磁导，；λe 为初级绕组端部漏磁导，，ky 为初级绕组短距系数，，βy=y(m1q1)-1，y为初级绕组短节距；λd 为谐波漏磁导，，kβ 由旋转感应电机设计书[10]得出，λs 为槽漏磁导，；αs1、αs2为初级“半填充槽”原因而引起的调整系数(若忽略“半填充槽”的影响，则αs1→1、αs2→1)，有；Kcu, Kk为绕组短距引起的调整系数，由λs可知，直线感应电机的槽漏磁导计算公式与普通旋转电动机的改进之处在于多了两个改进系数αs1和αs2，当2p为无限大时，取值都等于1.

2 改进的SLIM T-型等值电路模型特性

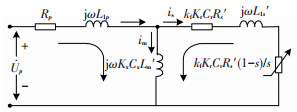
通过上述分析可以得到端部效应影响的SLIM改进等值电路T-模型[12]，如图 1所示.

图 1 考虑各类端部效应影响后的SLIM等效电路改进T-模型

改进后的T型等值电路与普通旋转感应电动机的等值电路依然相似，所不同的是前者多了由端部效应引起的4个改进系数 Kr、Kx、Cr、Cx.这4个系数都是电机几何尺寸、次级导体材料和滑差率的函数.利用这4个改进系数，就可以像计算普通RIM的特性一样计算SLIM的各种特性(在恒流源或恒压源调节模式下)[13].

2.1 T-模型改进后各参数的相应调整

根据图 1的电压电流回路方程，应用基尔霍夫电压定理，可得

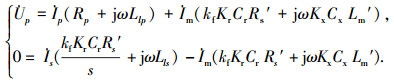
次级的电磁有功功率输出

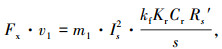
可得

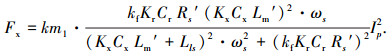
(9)

定义3个自由系数 Ax，Cx和Dx，式(9)简化为

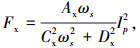
(10)

式中，各系数调整为

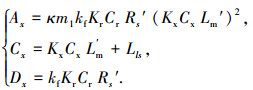
对应式(10)的最大推力输出点的最优滑差频率以 fs, optimum (Hz)标记，也需要作相应的计算调整为

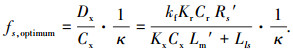
次级等效感应电阻 Rs′互感参量Lm′作相应的计算调整如下:

2.2 观测偏差对输出性能影响的仿真分析

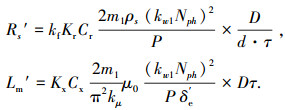
SLIM最终的电磁推力输出精度将直观反映为初级电流的重构精度上，又可将实际电流与重构电流的差别分为幅值不匹配和相位不匹配两方面[7, 14]，并从这两个点及其组合上分别讨论观测偏差对输出推力的最终影响.为便于观察并考虑实际运行工况，仿真实验取电流参数：幅值偏差0.05 A/0.1 A，相位偏差(π/20)/(π/10)，相关实验结果如下.

1) 当 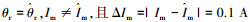或0.05 A时，实测推力与观测器重构推力输出特性如图 2所示.

图 2 重构电流与实际电流幅值不匹配

2) 当 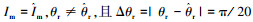或π/10时，实测推力与观测器重构推力输出特性如图 3所示.

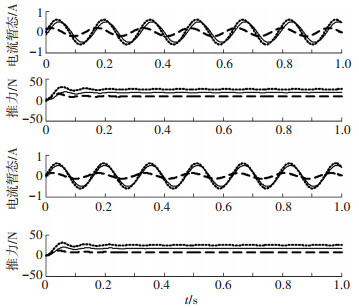
图 3 重构电流状态与实际电流相位不匹配(Δθr=π/20或π/10)

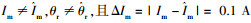
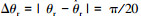
3) 当或0.05 A时，或π/10时，实测推力与观测器重构推力输出特性如图 4(a)、4(b).

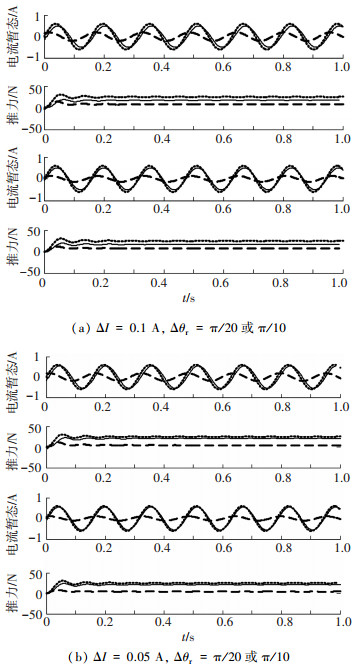
图 4 重构电流状态与实际电流幅值、相位均不匹配

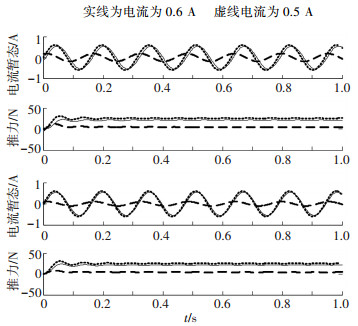
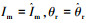
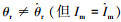
4) 假定在 t < 0.5 s之前，；而在t≥ 0.5 s以后，有，如图 5(a)所示；或，如图 5(c)所示；实测推力与观测器重构推力在瞬时不匹配的累计积分偏差下输出特性如图 5(b)、5(d)所示.

图 5 重构电流状态瞬时不匹配偏差特性

图 5 (a)中实线电流为0.55 A，相位为0；虚线电流为0.6 A, 相位为0. 图 5(b)中推力实线电流为0.55 A，相位为 π/10；虚线电流为0.6 A, 相位为0. 图 5(c)中实线电流为0.6 A，相位为π/10;虚线为0.6 A，相位为0. 图 5(d)中实线电流为0.6 A，相位为π/20;虚线电流为0.6 A，相位为0.

由图 2~5仿真实验结果可知，SLIM电流辨识状态对输出电磁推力的辨识精度主要的影响在于电流幅值的辨识差别，电流相位偏差都可以在累计积分计算中逐步消除.本文采用纵、横向端部效应的影响来改进电机的等值计算模型，目的是为了改进相应的幅值计算参量，这样即能实现辨识电流与实际控制电流的较小偏差，也实现了对精度的提高.

3 磁浮模拟平台实验

模拟磁悬浮驱动的直线电机牵引系统实验平台如图 6所示.

图 6 磁悬浮直线电机牵引系统实验平台

通过采用改进T-模型后电机的算法进行实用性验证.该实验平台的驱动悬浮控制原理与中低速磁悬浮系统基本原理是一样的，但结构尺寸不同，所研究的控制算法具有通用可移植特性.对于边端极磁场畸变及不规则发散状态，等价为电流状态值在实数变化区域映射到双曲正切函数上[15].因此，本文需要对前文献[14]中公式稍加修正为

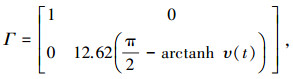
其中，对任意实数区域的输入状态 υ(t)，均满足：|arctanh(υ(t))| < π/2.

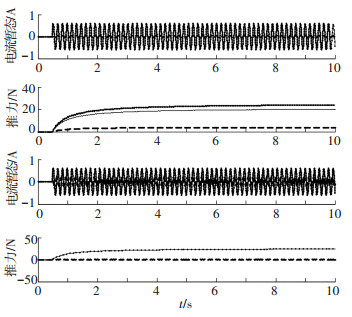
图 7~9为模拟实验台的应用实验结果，其中各示波器所得动态波形中：通道1(CH1)为实测电流状态(表征实际速度)，通道2(CH2)为辨识重构电流状态(表征辨识速度)，通道M(M)为状态偏差信号(表征估算偏差).

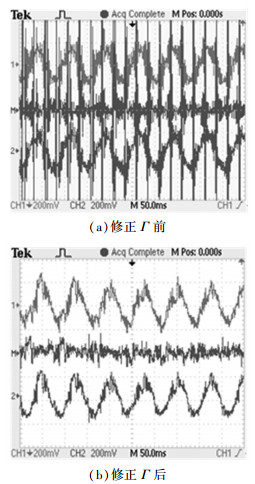
图 7 畸变磁场区域实测电流与重构输出动态波形
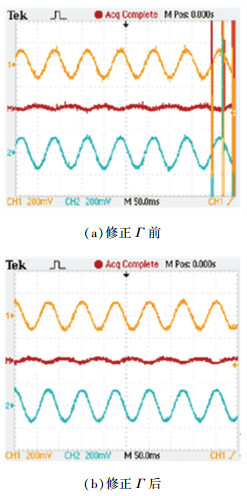
图 8 实测电流与重构输出动态波形

状态偏差越小在实际的惯性牵引中，电机的速度辨识精度越高，从而表明了改进电路拓扑以后各控制算法的性能都有了一定程度的提升.

实验结果分析：1)采用修正的正定滤波矩阵 Γ 以后，见图 7，电机穿越边端极磁场区域电流的发散状态被有效抑制，电流重构状态不论是幅值还是相位上与实际状态也基本吻合；2)考虑SLIM的端部效应及“集肤效应”并对电机的等效控制电路进行改进以后，并引入了修正以后的各类动态参数计算，电机重构的输出状态与实际输出状态，不论是低速还是高速恒定运行工况下，还是加减速的动态变化区域，相互偏差都很小如图 8、9所示.

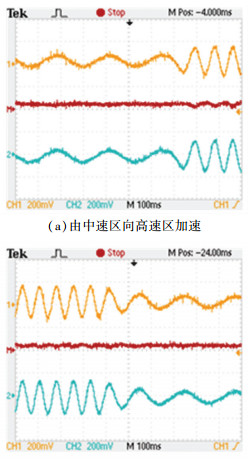
图 9 采用改进T-模型以后电机突变速度运行工况下，重构状态与实际输出状态动态波形
4 结论

1) 在对电机的T-型等效电路的改进的基础上，并引入与电机几何尺寸、次级导体材料、和滑差率有关的4个改进系数 Kr、Kx、Cr、Cx，利用改进的电机T-模型，并提高了其品质因数，且不影响SLIM在无速度传感器策略下的可观性.

2) 通过仿真实验，表明各动态参数幅值的修正对提高电机速度辨识精度是有利的.在中低速磁悬浮模拟实验平台上进行两个方面的实验验证：结合互联观测器设计原理，重新修正了正定等效滤波矩阵 Γ，使得SLIM即使在穿越磁场畸变区域，也能够获得良好的电流状态观测；验证了在改进后的T-模型下，电机的状态辨识效果，表明重构电流状态，不论在动态变化过程还是稳态精度，基本能够复现实际电流状态，也即电机的辨识速度精度已经达到了较高程度.

参考文献
[1]
CHEN W H, BALANCE D J, GAWTHROP P J, et al. A nonlinear disturbance observer for robotic manipulators[J]. IEEE Transactions on Industrial Electronics, 2000, 47(4): 932-938. DOI:10.1109/41.857974
[2]
ALFREDO M G, THOMAS A L, DONALD W N. A new induction motor V/f control method capable of high-performance regulation at low speeds[J]. IEEE Transactions on Industry Applications, 1998, 34(3): 813-821.
[3]
LIU H X, LI S H. Speed control for PMSM servo system using adaptive functional control and extended state observer[J]. IEEE Transactions on Industrial Electronics, 2012, 59(2): 1171-1183. DOI:10.1109/TIE.2011.2162217
[4]
SHIN H B, PARK J G. Anti-windup PID controller with integral state predictor for variable-speed motor drives[J]. IEEE Transactions on Industrial Electronics, 2012, 59(3): 1509-1516. DOI:10.1109/TIE.2011.2163911
[5]
黄坚, 郭中醒. 实用电机设计计算手册[M]. 上海: 上海科学技术出版社, 2010: 233-238.
[6]
AMIR Z B, MOHAMMAD R N, MOHAMMAD R M. Optimum design of single-sided linear induction motors for improved motor performance[J]. IEEE Transactions on Magnetics, 2010, 46(11): 3939-3947. DOI:10.1109/TMAG.2010.2062528
[7]
YU Xinghuo, WANG Bin, LI Xiangjun. Computer-controlled variable structure systems:the state-of-the-art[J]. IEEE Transactions on Industry Information, 2012, 8(2): 197-205. DOI:10.1109/TII.2011.2178249
[8]
斯蒂芬·查普曼. 电机学[M]. 5版. 刘新正, 译. 北京: 电子工业出版社, 2012: 56-63.
[9]
SHIRI A, SHOULAIE A. Design optimization and analysis of single-sided linear induction motor, considering all phenomena[J]. IEEE Transactions on Energy Conversion, 2012, 27(2): 516-525. DOI:10.1109/TEC.2012.2190416
[10]
BOLOGNANI S, PRETTI L, ZIGLIOTTO M. Design and implementation of model adaptive control for electrical motor drives[J]. IEEE Transactions on Industrial Electronics, 2009, 56(6): 1925-1936. DOI:10.1109/TIE.2008.2007547
[11]
KIM D K, KWON B I. A novel equivalent circuit model of linear induction motor based on finite element analysis and its coupling with external circuits[J]. IEEE Transactions on Magnetics, 2006, 42(10): 3407-3409.
[12]
VACLAVEK P, BLAHA P. AC induction machine speed observer with rotor resistance adaptation[C]//Proc 16th IFAC World Congress. Praha, Czech Republic: International Federation of Automatic Control Press, 2005: 1728-1734.
[13]
邓江明, 陈特放, 唐建湘. 单边直线感应电机动态最大推力输出的滑差频率优化控制[J]. 中国电机工程学报, 2013, 33(12): 123-130.
[14]
GINOYA D, SHENDGE P B, PHADKE S B. Sliding mode control for mismatched uncertain system using an extended disturbance observer[J]. IEEE Transactions on Industrial Electronics, 2014, 61(4): 1983-1992. DOI:10.1109/TIE.2013.2271597
[15]
THOMAS J, HANSSON A. Speed tracing of a linear induction motor-enumerative nonlinear model predictive control[J]. IEEE Transactions on Control Systems Technology, 2013, 21(5): 1956-1962. DOI:10.1109/TCST.2012.2217745