注浆是一种在当前实际工程实践中应用非常广泛的岩土施工技术,已遍及建筑、公路、铁路、地铁、矿山、隧道、水电、军事、边坡、冶金等较多工程领域[1].依据不同的流变本构方程将注浆流体主要分为牛顿流体、宾汉姆流体及幂律型流体3类[1-2];而这些流体在被注介质或材料中的渗透注浆可表现球面、柱面及柱-半球面3种扩散形式[2].
目前,牛顿流体及宾汉姆流体的渗透注浆扩散理论取得的成果较多,而在幂律型流体渗透注浆扩散机理方面开展的研究工作则非常少.在牛顿流体方面,以Maag公式及柱面渗透注浆扩散理论等为典型代表[1-2];此外,Baker探讨了牛顿流体在岩体裂隙内的最大扩散半径计算公式[3],邹金锋研究了在平面径向圆形裂缝中牛顿流体的扩散规律[4],文献[5-6]分析了考虑粘度时变性牛顿流体在均匀砂层中的渗透注浆计算方法及一维层流运动时的压力变化规律等.对于宾汉姆流体,文献[7-10]都对宾汉姆流体在岩体裂隙中的注浆扩散理论开展过研究;文献[11-12]推导了宾汉体浆液的砂土渗透与海底隧道劈裂注浆机理;文献[13-14]研究了考虑宾汉体浆液粘度时变性特性的岩体裂隙及隧道劈裂注浆理论;文献[15-16]对黏度时变性宾汉流体的球形、柱形与呈柱-半球形渗透注浆机理进行了探讨.然而,在幂律型流体渗透注浆机理方面,分析当前的国内外文献发现,仅有文献[17-19]对其以球形及柱形方式的渗透注浆扩散机理开展过一定的研究,但在推导其柱形渗透注浆扩散公式过程中,将注浆量表达式写为 Q=2πl1hφ[18-19],而一般注浆量表达应为Q=π(l1)2hφ,即在柱形渗透注浆扩散过程中,注入的注浆量应为被注入的被注介质的空间体积与孔隙率的乘积,而非空间表面积与孔隙率的乘积(其中Q为注浆量,l1为流体的最终扩散半径;h为柱形扩散高度,φ为被注介质的孔隙率),因此其模型不能准确反映幂律型流体在被注介质或材料中的柱形注浆渗透扩散规律.
当前,幂律型流体广泛地运用于实际注浆工程,如在工程中常用的水灰(质量)比 W/C 在0.5~0.7之间的水泥液浆属于典型的幂律型流体[20-21].然而,目前较贫乏的幂律型流体注浆理论难以满足工程实践的需要及保证实际的注浆效果.因此,本文对幂律型流体的柱形渗透注浆机制开展一些研究与探讨,以期为实际注浆施工提供一定的理论支撑.
1 幂律型流体柱形渗透注浆机制 1.1 幂律型流体基本流变方程及渗流运动方程
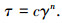
|
(1) |
参考文献[5, 8]可得到幂律型流体在被注介质或材料中的渗流运动方程为
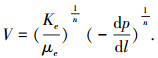
|
(2) |
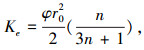
|
(3) |
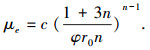
|
(4) |
式中: V 为幂律型流体的渗流速度;τ 为剪切应力;n 为流变指数;γ 为剪切速率,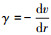
根据文献[22-24],本文在探讨幂律型流体柱形渗透注浆机制时采用如下假设:1)被注介质或材料满足各向同性与均质;2)流体为不可压缩且在注浆过程中流型保持不变;3)流速较小,浆液除了在注浆孔周围局部区域的流态呈紊流状态外其余皆为层流;4)采用填压法注浆,流体从注浆管侧面孔注入被注介质且呈柱面扩散;5)幂律型流体的重力影响作用在注浆过程中忽略不计.
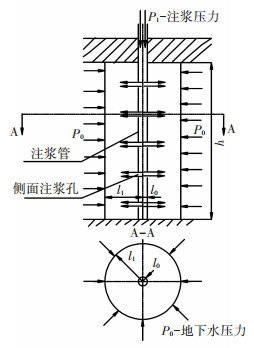
本文在研究幂律型流体柱形渗透注浆机制时采用的扩散理论模型见图 1.
|
图 1 幂律型流体柱形扩散理论模型 |
在图 1中,p1 为注浆压力;p0 为注浆点处的地下水压力;l1 为第 t 时刻幂律型流体扩散半径;l0 为注浆孔半径;h 为幂律型流体柱形扩散高度.
因流体在注浆过程中的注浆量 Q 满足
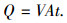
|
(5) |
式中 A 为幂律型流体在注浆区域扩散的总表面积.
图 1所示的幂律型流体在柱形扩散理论模型下的扩散总表面积 A 可表示为
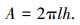
|
(6) |
将式(5)、(6)代入式(2),得
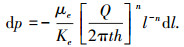
|
(7) |
对式(7)采用分离变量法积分且考虑注浆边界条件,即 p=p1时,l=l1;p=p0时,l=l0,得
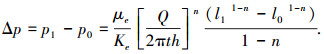
|
(8) |
又由注浆量 Q=πl12hφ,可得幂律型流体柱形渗透注浆扩散机理公式为
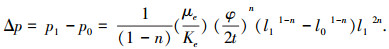
|
(9) |
幂律型流体柱形渗透注浆扩散机理公式是假设流体为层流运动状态为基础开展推导的,因此对于紊流不适用.根据文献[25],幂律型流体的层流或紊流状态一般常采用其稳定性系数 Z来确定.当Z < 808时,幂律型流体为层流态;而Z>808时,其则为紊流流态.其稳定性系数Z值可通过下式计算得到,即
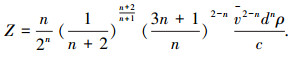
|
(10) |
式中:ρ 为幂律型流体的密度;d 为流体运动的范围尺寸(如管径,文中指流体在被注介质中通过的孔隙尺寸);v 为其在被注介质与材料中流动的平均速度.
2.2 参数确定方法对于式(9)孔隙度 φ 为被注介质或材料中孔隙体积与总体积二者的比例,即
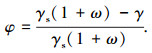
|
(11) |
式中:ω 为被注介质或材料的含水率;γ 为天然重度;γs 为其土粒容重.这些参数可以依据文献[26]测定.
被注介质或材料的渗透系数 K 反映了其渗透特性,可采用室内或野外现场测定方法确定,但为真实地反映被注介质或材料的渗透性,常采用现场注水试验的方法获得.
注浆时间 t 可根据实际工程情况或现场经验设计选取,而注浆管半径 l0 可采用直接测定多次并取平均值确定.
幂律型流体的稠度系数 c 与流变指数 n 可采用以下两种方法中的一种获得:1)依据目前已取得的幂律型流体的流变特征的研究成果获取,如文献[20, 22-23]等;2)采用毛细管黏度计或旋转黏度计等流体粘度计进行测量、分析与计算获取.
在获得被注介质或材料的孔隙度 φ 与渗透系数 K 的基础上,通过查询不同温度下水的粘度 μ 值,依据式 K=φr02/8μ 计算得到 r0;再由式(3)、(4)分别计算得到对应的幂律型流体的有效渗透率 Ke 与有效粘度 μe 参数.
至此,式(9)需要获取的各个参数均完全确定,在已知注浆压力与注浆点地下水压力差 Δp 条件下能求解得到幂律型流体在被注介质或材料中的柱形渗透注浆的理论扩散半径 l1;反之,已知 l1,能求出其理论上的注浆压力差 Δp.
3 验证试验为验证本文推导的幂律型流体柱形渗透注浆扩散机理公式的正确性,本文将设计室内注浆实验对其开展验证.
3.1 注浆实验装置本文采用如图 2所示的注浆实验装置. 图 2所示的注浆试验装置由供压装置、储浆容器和试验箱3部分组成,实物图见图 3.供压装置采用有压氮气为注浆提供注浆压力,且通过调节氮气减压器与注浆控制开关可实现对注浆试验过程中注浆压力与注浆时间的精确定量控制.试验箱是用来放置被注介质的设备,是完成注浆整个实验过程的装置.储浆容器用来盛装幂律型流体,在注浆过程中,通过电子称可较精确测量在整个注浆试验过程中注入被注介质的幂律型流体量.
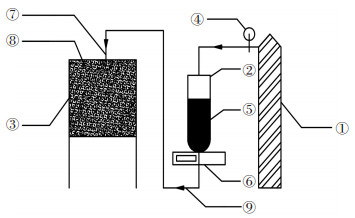
|
1—供压设备;2—储浆容器;3—试验箱;4—氮气减压器与注浆控制开关;5—幂律型流体;6—电子称;7—注浆管;8—粒径较均匀的砾(砂)石体;9—注浆导管 图 2 注浆验证试验装置示意 |

|
图 3 注浆试验装置实物 |
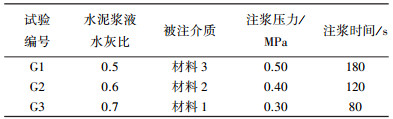
注浆材料选用昆明水泥厂生产标号为#32.5的普通硅酸盐水泥.该标号水泥在目前工程上广泛运用作为注浆材料.在本文的注浆验证实验中,分别配置水灰比为0.5、0.6、0.7的水泥浆液,据文献[20-21, 27]可知,这3种水泥浆液为典型的幂律型流体.它们各自的流变方程可见文献[20]的研究成果.
本文选取颗粒粒径分别分布在5~10 mm、3~5 mm及1~3 mm之间的砾(砂)石体作为验证实验的被注介质.为使这3种被注的砾(砂)石体最大限度满足各向同性与均质假设,在注浆试验开展前在清水中洗淘3次. 3种被注砾(砂)石体材料的性质见表 1.
| 表 1 3种被注砾(砂)石体材料性质 |
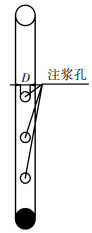
本文的注浆验证实验的设计参数见表 2.设计的注浆试验采用的注浆管均为直径为15 mm的PVC管,开展试验的室内环境温度及实验用水的水温均为10 ℃(10 ℃时水的黏度 μ=1.31× 10-3 Pa·s). 注浆管上设计的注浆孔个数为3个,其分布情况见图 4.注浆验证实验过程的实物照片见图 5.
| 表 2 幂律型注浆实验设计参数 |
|
图 4 注浆管上注浆孔分布 |

|
图 5 注浆试验过程实物 |
在开展表 2设计的验证注浆实验前,首先必须采用式(10)来判定幂律型水泥浆液在被注砾(砂)石体中的流动状态.对于表 2中的注浆实验,先计算在配置好幂律型水泥浆液瞬间其在注浆管中流动的稳定性系数.
水灰比为0.5的水泥浆液的 Z0.5b= 324.74;水灰比为0.6的水泥浆液的 Z0.6b= 34.27;而水灰比为0.7的幂律型水泥浆液的 Z0.7b= 11.51.随着这3种幂律型水泥浆液被注入砾(砂)石体,其稠度逐渐增大,引起浆液在被注的砾(砂)石体中可流动的孔隙尺寸及平均运动速度均逐步减小,因此导致在注浆过程中水泥浆液的瞬时稳定性系数 Zs 也相应逐步降低,即在注浆过程中,水灰比分别为0.5、0.6及0.7的幂律型水泥浆液的瞬时稳定性系数 Zs 均满足关系 Zs < Zb < 808. 表明本文设计与开展的注浆验证试验采用的水灰比0.5、0.6、0.7的水泥浆液在被注砾(砂)石体的注浆过程中都符合层流状态理论基础.
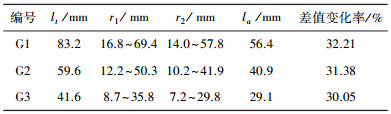
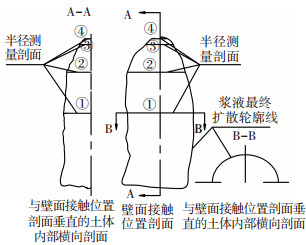
3.3.3 结果分析分析实验结果可知,幂律型水泥浆液在被注砾(砂)石体中表现为下半部分圆柱型而上半部分半椭球体的扩散形态,与理论上应完全呈圆柱型的扩散形状具有一定的差异;同时,在壁面接触面上的扩散半径大于与其垂直的土体内部纵向剖面上对应的扩散半径.幂律水泥浆液在被注砾(砂)石体中的扩散规律与特征见图 6.
|
图 6 幂律型水泥浆液在被注砾(砂)石体的扩散规律 |
根据图 6所示的幂律型水泥浆液在被注砾(砂)石体中的扩散规律与特征,为更好地分析验证式(9)幂律型流体柱形渗透注浆扩散机理公式的适用性,本文在壁面接触平面与与其垂直的土体内部纵向平面上选取不同的注浆剖面进行浆液扩散半径测量,选取的测量剖面具体位置见图 6所示的①、②、③、④.其中①测量面约在结石体实际扩散高度一半处,该位置到注浆结石体底部间的部分浆液较完全的呈圆柱型扩散;②测量面与①测量面间的距离约为结石体实际扩散高度的30%,③测量面在设计的柱形扩散高度位置处,④测量面在实际的柱形扩散高度位置处,在这3个测量面间的被注砾(砂)石体中浆液呈半椭球体态扩散,且随着向上其浆液扩散半径逐渐减小.
为综合比较幂律型水泥浆液在被注砾(砂)石体中的柱形扩散整体效果与式(9)计算的理论扩散半径的差异,本文采用等体积法来计算幂律型流体在被注砾(砂)石体中的等效扩散半径,即
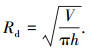
|
(12) |
式中:Rd 为幂律型流体在被注砾(砂)石体中的等效扩散半径;V 为注浆结石体的扩散体积,可由实际测量及计算得到;h 为注浆结石体的扩散高度,可实测得到.
注浆结石体在4个测量面上的壁面接触面的扩散半径与与壁面接触平面垂直的土体内部纵向平面的扩散半径及扩散高度可用卷册或直尺均分别至少测量3次后,取其平均值确定.注浆试验完成且待水泥浆液与被注砾(砂)石体一起完全固结与变干后,拆卸试验箱,用卷册测量注浆结石体扩散半径及扩散高度,且至少测量3次,取其平均值,保证它们的标准差不超过5%,测量结果见表 3.
| 表 3 注浆试验的整体综合效果结果分析 |
依据式(12)可计算得到幂律型水泥浆液在被注砾(砂)石体中的等效扩散半径.根据幂律型流体柱形渗透注浆扩散机理公式得到的扩散半径理论计算值与实际测量计算的等效扩散半径及二者间的差值分析见表 3. lt 为计算的注浆扩散半径理论值半径理论值,r1 为壁面接触面的扩散半径,r2 为与壁面接触平面垂直的土体内部纵向平面的扩散半径,la 实际测量计算的等效扩散半径.
分析表 3,由推导的幂律型流体柱形渗透注浆扩散机理公式计算出的注浆扩散半径理论值大于在注浆试验中的实际测量计算的等效扩散半径,二者具有30%~35%的差异.国外一些研究表明,试验实际测量值与理论计算值二者间的差异在-50%~100%内都是可接受的误差范围,并在国内的试验研究中得到较广泛的运用[21, 27].因此,本文建立的幂律型流体柱形渗透注浆扩散机理在总体上能较好地反映幂律型流体在被注介质中的柱形注浆渗透扩散规律,可为实际注浆施工提供理论支撑与指导作用.
采用本文推导的幂律型流体柱形渗透注浆扩散机理公式计算出的扩散半径理论值大于注浆试验的实际测量值的原因主要有以下3个方面:1)较多因素影响幂律型水泥浆液在被注介质中渗透扩散效果,如水泥浆液可能会出现沉淀、堵塞与滤水等实际扩散问题;又如在注浆试验中,配置的幂律型水泥浆液一般因析水率等性能的超标常为不稳定浆液,而在采用幂律型流体柱形渗透注浆扩散机理公式计算理论值时假设水泥浆液为稳定性浆液. 2)选择颗粒粒径分布较均匀的砾(砂)石体作为被注介质,且在试验前淘洗3次,虽然能最大限度地满足各向同性与均质假设,但还是不能达到推导理论公式的完全均质和各向同性的假设要求. 3)未考虑幂律型水泥浆液的时变性,这点本文认为是最主要的原因.
4 结论1) 以幂律型流体流变方程及渗流运动方程为基础,推导了幂律型流体柱形渗透注浆扩散机理.
2) 设计室内注浆实验验证了推导的幂律型流体柱形渗透注浆扩散机理.实验结果表明:注浆实验的实际测量计算的等效扩散半径值与由幂律型流体柱形渗透注浆扩散机理公式计算出的扩散半径理论值间具有30%~35%的差异,但是这些差异都处于可接受误差范围内,因而能较好地反映幂律型流体在被注介质中的柱形注浆渗透扩散规律,可为实际注浆施工提供理论支撑与指导作用.
| [1] |
《岩土注浆理论与工程实例》编写组. 岩土注浆理论与工程实例[M]. 北京: 科学出版社, 2001: 51-106.
|
| [2] |
王国际. 注浆技术理论与实践[M]. 北京: 中国矿业大学出版社, 2000: 98-116.
|
| [3] |
BAKER C. Comments on paper rock stabilization in rock mechanics[A]. NY: Springer-Verlag NY, 1974: 45-78.
|
| [4] |
邹金锋, 李亮, 杨小礼. 劈裂注浆扩散半径及压力衰减分析[J]. 水利学报, 2006, 37(3): 314-319. |
| [5] |
郑大为, 张彬, 王笑冰. 粘度渐变型浆液渗透注浆灌注均匀砂层计算方法的研究[J]. 岩石力学与工程学报, 2005, 24(增刊1): 5086-5089. |
| [6] |
石达民, 吴理云. 关于注浆参数研究的一点探索[J]. 矿山技术, 1986, 2: 14-16. |
| [7] |
LOMBARDI G. 水泥灌浆浆液是稠好还是稀好[C]//现代灌浆技术译文集. 北京: 水利电力出版社, 1991: 76-81. http://cpfd.cnki.com.cn/Article/CPFDTOTAL-ZGYJ199108002012.htm
|
| [8] |
刘嘉材. 裂隙灌浆扩散半径研究[C]//中国水利电力科学研究院科学研究论文集: 第8集. 北京: 水利出版社, 1982: 232-233.
|
| [9] |
郑长成. 裂隙岩体灌浆的模拟研究[D]. 长沙: 中南工业大学, 1999.
|
| [10] |
杨晓东, 刘嘉材. 水泥浆材灌入能力研究[C]//中国水利电力科学研究院科学研究论文集: 第27集. 北京: 水利电力出版社, 1987: 184-191.
|
| [11] |
杨秀竹, 王星华, 雷金山. 宾汉体浆液扩散半径的研究及应用[J]. 水利学报, 2004, 35(6): 75-79. |
| [12] |
孙锋, 张顶立, 陈铁林, 等. 基于宾汉体浆液的海底隧道劈裂注浆机理研究[J]. 北京交通大学学报, 2009, 33(4): 01-06. |
| [13] |
阮文军. 基于浆液黏度时变性的岩体裂隙注浆扩散模型[J]. 岩石力学与工程学报, 2005, 24(15): 2709-2714. DOI:10.3321/j.issn:1000-6915.2005.15.018 |
| [14] |
孙锋, 张顶立, 陈铁林. 基于流体时变性的隧道劈裂注浆机理研究[J]. 岩土工程学报, 2011, 33(1): 88-93. |
| [15] |
杨志全, 侯克鹏, 郭婷婷, 等. 基于考虑时变性的宾汉姆流体的渗透注浆机理研究[J]. 四川大学学报(工程科学版), 2011, 43(增刊1): 67-72. |
| [16] |
杨志全, 侯克鹏, 郭婷婷, 等. 粘度时变性宾汉体浆液的柱-半球形渗透注浆机理研究[J]. 岩土力学, 2011, 32(9): 2698-2703. |
| [17] |
杨秀竹, 雷金山, 夏力农, 等. 幂律型浆液扩散半径研究[J]. 岩土力学, 2005, 26(11): 1803-1806. DOI:10.3969/j.issn.1000-7598.2005.11.019 |
| [18] |
杨秀竹. 静动力作用下浆液扩散理论与实验研究[D]. 长沙: 中南大学, 2005. http://cdmd.cnki.com.cn/Article/CDMD-10533-2006043279.htm
|
| [19] |
李慎刚. 砂性地层渗透注浆试验及工程应用研究[D]. 沈阳: 东北大学, 2010. http://cdmd.cnki.com.cn/Article/CDMD-10145-1013117060.htm
|
| [20] |
阮文军. 注浆扩散与浆液若干基本性能研究[J]. 岩土工程学报, 2005, 27(1): 69-73. |
| [21] |
阮文军. 浆液基本性质与岩体裂隙注浆扩散研究[D]. 吉林: 吉林大学, 2003.
|
| [22] |
沈崇棠, 刘鹤年. 非牛顿流体力学及其应用[M]. 北京: 高等教育出版社, 1989: 147-177.
|
| [23] |
孔祥言. 高等渗流力学[M]. 北京: 中国科学技术大学出版社, 1999: 315-332.
|
| [24] |
ZENIT R, KOCH D L, SANGANI A S. Measurement of the average properties of a suspension of bubbles rising in a vertical channel[J]. J Fluid Mech, 2001, 429: 2-3. |
| [25] |
曾祥熹. 泥浆流变学与粘度测量[M]. 湖南: 湖南地质学会, 1981: 34-53.
|
| [26] |
中华人民共和国水利部. 土工试验方法标准: GB/T 50123-1999[S]. 北京: 中国计划出版社, 1999.
|
| [27] |
阮文军. 基于浆液黏度时变性的岩体裂隙注浆扩散模型[J]. 岩石力学与工程学报, 2005, 24(15): 2709-2714. DOI:10.3321/j.issn:1000-6915.2005.15.018 |
 2016, Vol. 48
2016, Vol. 48