2. 哈尔滨工业大学 卫星技术研究所 150001 哈尔滨;
3. 空间物理重点实验室(北京临近空间飞行器系统工程研究所) 100076 北京
2. Research Center of Satellite Technology, Harbin Institute of Technology, 150080 Harbin, China;
3. Science and Technology on Space Physics Laboratory(Beijing Institute of Nearspace Vehide's Systems Engineering), 100076 Beijing, China
利用多个小型飞行器组网编队替代传统单个大型飞行器执行空间飞行任务,具有成本低、可靠性高、执行任务灵活及功能性强等诸多优点.因此多空间飞行器编队飞行问题在近年来受到国内外学者的广泛关注与深入研究.飞行器编队中一个关键的问题是多飞行器间的姿态协同问题,由于其在空间干涉测量及三维立体成像中的重要应用,国内外学者[1-3]开展了相关研究.文献[4-5]中针对航天器编队姿态协同控制问题提出了一种基于行为方式的控制方法,其本质思想是通过对不同行为的加权叠加来计算控制指令;文献[6]中基于滑模控制理论,提出一种基于行为方式的鲁棒姿态协同控制方法,能够在干扰力矩、模型参数不确定性及通信延迟存在的情况下实现编队姿态协同;文献[7]中考虑模型参数不确定性及干扰力矩有界的情况,提出有限时间控制方法能够在有限时间内实现编队系统的姿态协同;文献[8]研究了领航-跟随模式下无角速度测量信息的姿态协同控制方法,在这种控制方法作用下,编队系统仅依靠姿态信息就能够实现姿态协同;当编队中有多个领航者时,文献[9-10]研究编队系统的姿态抑制控制问题,所有跟随者的姿态都能够被控制在一个由领航者姿态所构成的凸集内.
在上述研究中,控制方法的提出均依赖于编队系统的期望姿态信息或领航者的姿态信息.但在编队的故障安全模式、初始姿态捕获阶段、对地观测任务间的姿态保持任务以及强干扰后的姿态恢复任务中,编队无法获取参考信息,此时需要进行自主编队姿态协同,即设计一种不依赖于外界参考信息或领航者姿态信息的姿态协同控制方法,使得飞行器编队能够进行自主协同控制.文献[11]利用能量成形方法解决了自主编队航天器在有限通信条件下的协同问题.需要指出的是,上述文献中均没有考虑干扰力矩的影响.而在实际情况中,如重力梯度力矩、太阳光压力矩、地磁力矩及气动力矩等空间干扰力矩会对飞行器编队产生很大影响.针对上述问题,本文研究了无外界参考信息的自主编队小型飞行器姿态协同控制问题,提出一种分布式姿态协同控制器,使小型飞行器编队能够在干扰力矩作用下实现姿态协同.首先,采用四元数表达方式描述了编队飞行器的姿态运动学模型.然后提出了分布式姿态协同控制方法,使编队系统能够在干扰力矩作用下实现姿态协同.该控制方法利用小型飞行器绝对姿态信息进行设计,且能够适应多种编队通信拓扑结构.最后,根据Lyapunov定理,从理论上证明了闭环系统的稳定性和收敛性.
1 数学模型及相关引理 1.1 姿态运动学和动力学模型本文中用四元数描述飞行器姿态,四元数的定义为
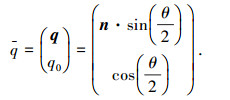
|
式中:q为四元数q的矢量部分;q0∈[0, 1]为四元数的标量部分;n为欧拉转轴方向;θ为欧拉主角,且四元数满足约束qTq+q02=1.
用四元数描述的飞行器姿态运动学方程为:
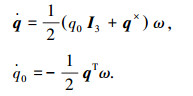
|
(1) |
式中:ω∈R3为本体系相对于惯性系的角速度在本体系下的分量;I3为一个3×3的单位阵;q×为一个反对称矩阵,表示如下
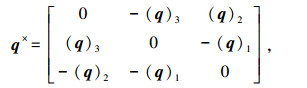
|
式中符号(v)k为向量v的第k个分量.
相对姿态qij表示的是两个飞行器i和j本体坐标系的相对旋转关系,其计算方法如下

|
式中:

|
编队中小型飞行器的动力学模型可用欧拉方程描述,如下
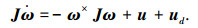
|
(2) |
式中:J=JT∈R3×3为飞行器的转动惯量矩阵;u∈R3为本体系下表示的控制矢量;ud∈R3为干扰力矩矢量,本文研究中假设干扰力矩是有界的,即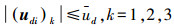
为方便后续分析,结合运动学方程式(1)和动力学方程式(2),推导出小型飞行器的拉格朗日模型,表达式为

|
(3) |
式中:A=QTJQ是一个半正定矩阵;B=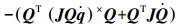

引理1[13] 若非线性系统
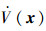

引理2[14] 设f(t)在[0, ∞)上是一致连续的,且存在p∈[1, ∞),使得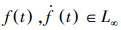

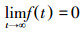
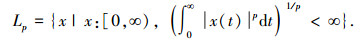
|
考虑由n个小型飞行器构成的自主编队系统.飞行器间的通信方式为双向且非全连接的,也即每个飞行器仅能和编队中部分飞行器进行信息交互.当干扰力矩存在且有界的情况下,自主编队小型飞行器的姿态协同控制问题可以表述为:编队中的每个飞行器设计合适的姿态协同控制律ui,使得编队中各飞行器的姿态协同,即当t→∞时,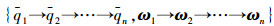
由于编队中成员仅能和其他部分成员进行通信,因此这里用Gi表示能与i飞行器进行通信的飞行器群体,mi表示Gi中元素的个数.协同控制方法设计如下
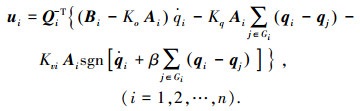
|
(4) |
式中:Ko、Kq分别为控制增益;
定理1 对于由式(3)描述的飞行器编队系统,所提出的控制器式(4)能够在干扰力矩存在且有界的条件下,实现自主小型飞行器编队系统的姿态协同,即当t→∞时,有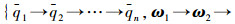

证明 考虑如下Lyapunov函数
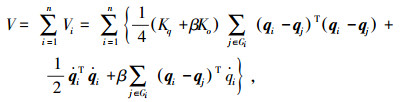
|
其中
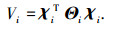
|
式中:
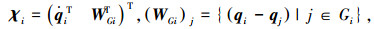
|
并且:
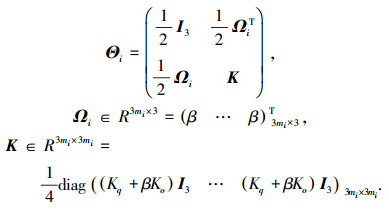
|
根据Schur补定理[15]可知,当参数β足够小时,矩阵Θi是正定的,于是V也是正定的.计算Vi的一阶导数,有
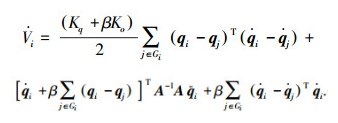
|
(5) |
将动力学方程式(3)代入到式(5),有
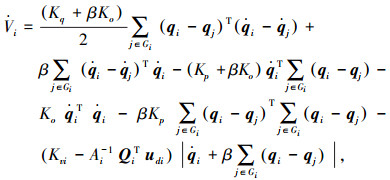
|
式中对于向量v有定义
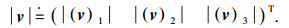
|
对于双向通信拓扑结构来说,有下式成立

|
于是,根据式(3)中矩阵A和Q的定义,可知Kvi-Ai-1QiTudi≥0,因此有
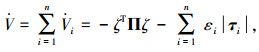
|
(6) |
其中
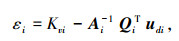
|
(7) |
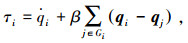
|
(8) |
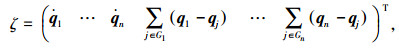
|
(9) |
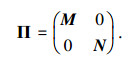
|
(10) |
其中
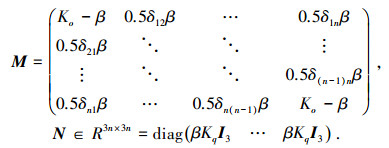
|
式中, δij=δji={0, 1}表示一个二进制数用以描述两个飞行器之间的通信连接情况.因此可知,如果εi≥0并且参数Ko、Kq和β选择合适(例如参数Ko和Kq远大于β),那么矩阵Π是正定的,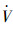
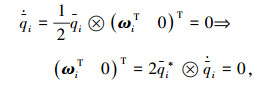
|
并且
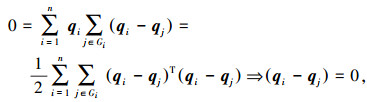
|
于是,控制目标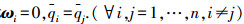
从另一方面,如果参数Ko、Kq和β的选择使得矩阵Π为半正定的,那么
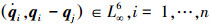


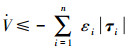
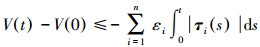
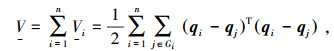
|
对其求一阶导数有

|
利用条件τi=0,有
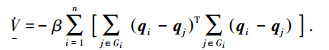
|
于是根据引理1可知qi=qj,且根据τi=0可知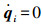
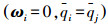
1) 控制器中的符号函数项能够保证编队系统在干扰力矩存在的情况下实现姿态协同控制,但也会在系统状态到达平衡点附近时导致控制信号出现抖颤现象.控制信号的抖颤需要极高的控制功率来实现,并且有可能激发在系统建模过程中被忽略的高频动态.因此,符号函数项在实际应用中可用饱和函数或双曲正切函数替代以消除抖颤现象.
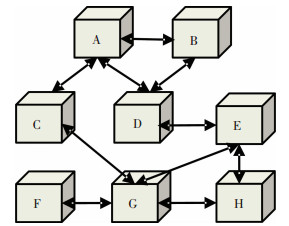
2) 在本文中所提出的通信拓扑结构中,每个成员仅需要和编队中部分其他成员进行通信,就能够保证编队的姿态协同.这种双向且部分连接的通信拓扑结构具有一定的普遍性,其涵盖了大部分编队构型,以4个小型飞行器编队为例,满足本文中通信拓扑结构的编队构型如图 1所示.

|
图 1 4种编队构型 |
考虑一个由8颗小型飞行器构成的编队,运行在轨道高度为400 km的近地圆轨道上,假设编队执行的空间任务为两次对地观测之间的姿态保持任务,考虑多种干扰因素的影响,通过数值仿真验证本文中提出的姿态协同控制算法的有效性.
各小型飞行器的转动惯量设定如下[16]:

|
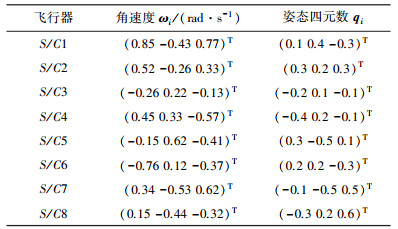
编队中各飞行器在对地观测任务后的空间姿态见表 1,该姿态也为姿态协同任务的初始姿态.
| 表 1 编队中各飞行器的初始姿态 |
在低轨道上,重力梯度力矩为主要干扰力矩,重力梯度力矩的计算方法如下[17]
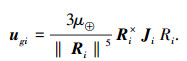
|
式中:ugi为重力梯度力矩; μ⊕为地球引力常数; Ri为第i个飞行器的轨道半径; Ji为飞行器转动惯量.为检验所提出控制器的抗干扰能力,仿真中干扰力矩选择如下
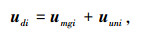
|
其中
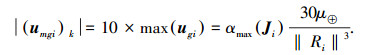
|
远大于飞行器所受到的重力梯度力矩为
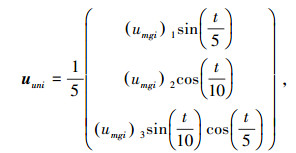
|
表示其他干扰力矩的影响,包括气动干扰力矩、太阳光压力矩、地磁力矩等.
由于编队中飞行器数量较多,为方便分析且使仿真结果更加直观,采用相对角速度误差度量和相对姿态误差度量两种度量标准来表示姿态协同的控制性能,度量标准的计算方法如下:
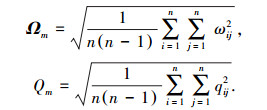
|
其中:Ωm为相对角速度度量标准,Qm为相对姿态度量标准.
编队小型飞行器的构型如图 2所示,每个飞行器均采用本文中提出的分布式姿态协同控制方法,控制参数选取为Kq=0.4,Ko=1.6,Kvi=0.01,β=0.3.
|
图 2 编队飞行器构型 |
仿真结果如图 3~6所示,图 3展示了编队系统相对角速度的度量标准曲线.图 4展示了编队系统相对姿态的度量标准曲线.作用于编队中各飞行器上的控制力矩曲线如图 5, 6所示.

|
图 3 姿态角速度度量标准 |
|
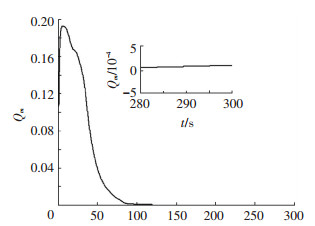
图 4 相对姿态度量标准 |
|
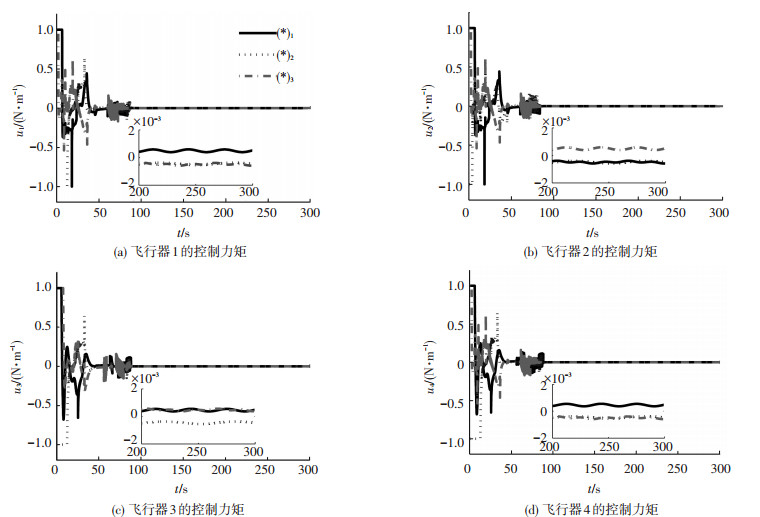
图 5 飞行器1-4的控制力矩曲线 |
|
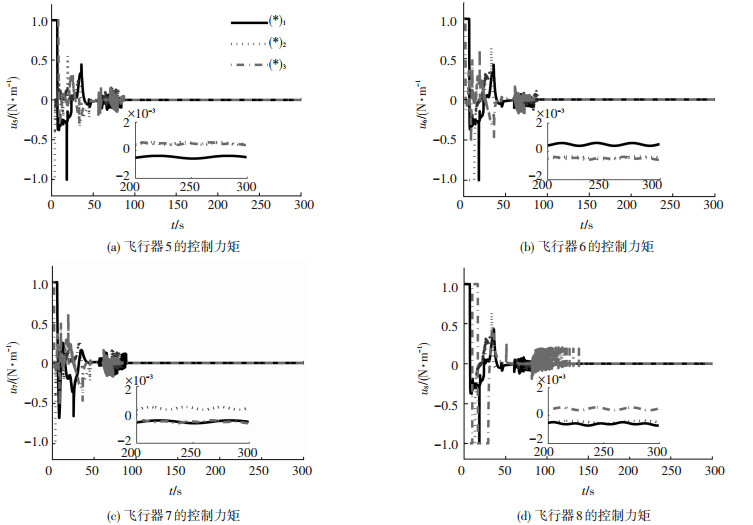
图 6 飞行器5-8的控制力矩曲线 |
从图 3, 4中可以看出,编队的姿态在约100 s后收敛,完成了编队姿态协同任务,且相对角速度控制精度优于1×10-5rad/s,相对姿态控制精度优于1×10-4.仿真结果表明,在较大的初始姿态偏差、空间干扰力矩及一般的编队构型下,所设计的控制方法能够实现自主编队飞行器的姿态协同.从图 5, 6中可以看出,由于使用饱和函数代替了符号函数项,控制信号仅在控制初期出现了短暂的抖颤现象,这可以通过增大饱和函数阈值的方式进一步消除,但需要说明的是,增大饱和函数阈值同时也会降低系统的控制精度,因此在实际应用中需根据控制要求和使用条件选取合适的阈值进行控制系统的设计.从图 5, 6中同时可以看出,在控制开始的时候,控制信号出现饱和的现象,这是因为仿真条件相对严酷,各飞行器间的相对姿态误差较大,从而导致前期控制信号过大,因此出现了饱和现象.需要说明的是,控制信号仅在开始一个极短的时间内发生饱和,而后随着控制误差的逐渐收敛,控制信号一直维持在一个很小的区间内,因此不会消耗过多能量.
4 结语本文针对多小型飞行器空间自主编队姿态协同飞行任务,研究了在干扰力矩作用下的姿态协同控制问题.当编队飞行器没有外界参考信息及领航者姿态信息时,进入自主编队模式.首先考虑了空间干扰力矩的影响,利用非线性控制方法及Lyapunov理论,提出了一种自主编队姿态协同控制方法.然后通过理论分析得出,所提出的控制方法能够利用小型飞行器绝对姿态信息实现编队姿态协同,且能够适应多种编队构型.最后采用数值仿真对所提出的控制方法进行了验证,考虑由8颗飞行器构成的自主编队姿态协同任务,仿真结果表明,所提出的控制方法能够实现在干扰力矩影响下的自主编队飞行器姿态协同.
| [1] |
WANG P K C, HADAEGH F Y. Coordination and control of multiple microspacecraft moving in formation[J]. Journal of the Astronautical Sciences, 1996, 44(3): 315-355. |
| [2] |
WANG P K C, HADAEGH F Y, LAU K. Synchronized formation rotation and attitude control of multiple free-flying spacecraft[J]. Journal of Guidance, Control and Dynamics, 1999, 22(1): 28-35. DOI:10.2514/2.4367 |
| [3] |
KANG W, YEH H H. Coordinated attitude control of multi-satellite systems[J]. International Journal of Robust and Nonlinear Control, 2002, 12(2/3): 185-205. |
| [4] |
VANDYKE M C, HALL C D. Decentralized coordinated attitude control within a formation of spacecraft[J]. Journal of Guidance, Control and Dynamics, 2006, 29(5): 1101-1109. DOI:10.2514/1.17857 |
| [5] |
LAWTON J, BEARD R W. Synchronized multiple spacecraft rotations[J]. Automatica, 2002, 38(8): 1359-1364. DOI:10.1016/S0005-1098(02)00025-0 |
| [6] |
JIN E, JIANG X, SUN Z. Robust decentralized attitude coordination control of spacecraft rmation[J]. Systems & Control Letters, 2008, 57(7): 567-577. |
| [7] |
LIANG H, WANG J, SUN Z. Robust decentralized coordinated attitude control of spacecraft formation[J]. Acta Astronautica, 2011, 69(5/6): 280-288. |
| [8] |
KRISTIANSEN R, LORIA A, CHAILLET A, et al. Spacecraft relative rotation tracking without angular velocity measurements[J]. Automatica, 2009, 45(3): 750-756. DOI:10.1016/j.automatica.2008.10.012 |
| [9] |
DIMAROGONAS D V, TSIOTRAS P, KYRIAKOPOULOS K J. Leader-follower cooperative attitude control of multiple rigid bodies[J]. American Control Conference, 2008, 58(6): 801-806. |
| [10] |
MENG Z, REN W, You Z. Distributed finite-time attitude containment control for multiple rigid bodies[J]. Automatica, 2010, 46(12): 2092-2099. DOI:10.1016/j.automatica.2010.09.005 |
| [11] |
SARLETTE A, SEPULCHRE R, AND LEONARD N E, Autonomous rigid body attitude synchronization. Automatica, 2009, 45:572-577[J]. Automatica, 2009, 45: 572-577. DOI:10.1016/j.automatica.2008.09.020 |
| [12] |
WU S, RADICE G, GAO Y, et al. Quaternion-based finite time control for spacecraft attitude tracking[J]. ACTA Astronautica, 2011, 69(s1/s2): 48-58. |
| [13] |
SLOTINE J E, LI W P. Applied nonlinear control[M]. New Jersey: Prentice Hall, 1991: 68-75.
|
| [14] |
SASTRY S, BODSON M. Adaptive control:stability, convergence, and robustness[M]. New Jersey: Prentice Hall, 1989: 18-19.
|
| [15] |
HORN R A, JOHNSON C R. Matrix analysis[M]. New York: Cambridge University Press, 1985: 472-473.
|
| [16] |
ALI I, RADICE G, KIM J. Backstepping control design with actuator torque bound for spacecraft attitude maneuver[J]. Journal of Guidance, Control, and Dynamics, 2010, 33(1): 254-259. DOI:10.2514/1.45541 |
| [17] |
PAN Haizhou, KAPILA V. Adaptive nonlinear control for spacecraft formation flying with coupled translational and attitude dynamics[C]//Proceedings of the 40th IEEE Conference on Decision and Control. Orlando, FL: IEEE, 2011.
|
 2016, Vol. 48
2016, Vol. 48