近年来一些先进控制理论与方法,如反馈控制[1]、自适应控制[2]、滑模控制[3-4]等及其相结合的复合控制方法在航天器实际系统控制中得到了一些应用,而滑模控制以其对不确定性的“不变性”受到学术界的广泛关注,并在航天器姿态控制中得到了广泛的应用[5-6].但是,对于传统的滑模控制,当系统到达滑模面时,存在滑模的到达过程,难以保证系统的动态性能.而积分滑模由于在系统中引入了状态的积分环节,一方面可以消除滑模面的到达过程,从而保证滑动模态下的系统与原始标称系统的一致性;另一方面,由于积分项的存在,将对常值干扰等具有很好的抑制作用;然而积分滑模控制及其在航天控制应用相关研究鲜见报道[7-8].
容错控制策略作为一种有效的手段来解决航天器的执行器故障问题而得到广泛的关注,其通过设计一类特定的控制算法来保证控制系统在故障模式下的稳定性与可靠性,并在航天航空领域得到了广泛的应用.文献[9]为解决卫星姿态跟踪控制问题中可能出现的执行器部分与完全失效故障,提出了一种自适应姿态容错控制器的设计方法;文献[10]在考虑模型不确定性、外干扰、执行器故障以及推力器力矩饱和受限的多种约束下,提出了一类鲁棒自适应容错控制器的设计方法.针对飞轮作为执行机构的故障情况下,基于动态逆和时延控制相结合的复合控制方法;文献[11]提出了一种类似迭代学习的卫星姿态容错控制方法.此外,考虑到对干扰以及不确定性项的抑制能力;文献[12]基于L-2增益方法,提出了一类航天器鲁棒姿态容错控制器的设计方法,该控制器再保证了系统的最终一致有界稳定的同时满足L-2性能指标要求.
然而,在这些容错控制方法的研究中,并没有考虑执行机构实际的物理约束,即没有显式地考虑控制力矩饱和受限的约束问题,而这种饱和受限的强非线性约束将会严重的影响系统的稳定性以及可靠性[13-14].此外,尽管上述文献所提出的控制方法能够解决航天器的外部干扰、饱和受限甚至执行器的故障容错问题,但它们并没有考虑实际系统存在执行机构安装偏差的问题.在实际的航天工程中,受限于安装工艺以及发射过程中运载器振动的影响,航天器执行机构的安装偏差不可避免.而这种安装偏差的存在将对姿态跟踪性能产生影响,严重时将使整个姿态控制任务失败.目前对执行器安装偏差问题的相关研究成果相对较少[15-16],然而在这些文献中,研究者们并没有考虑常值干扰对系统的影响.
为此,本文在上述研究成果的基础之上,综合考虑外部干扰、执行机构故障、安装偏差以及控制受限的多约束问题,提出一种新型自适应积分滑模姿态容错控制方法;该方法在显式地引入饱和函数以保证控制输出受限的同时,并不依赖于执行器的在线故障诊断信息;理论上证明了所设计控制系统对执行机构故障和安装偏差等的容错能力与鲁棒性以及系统的稳定性,并且数值仿真研究结果也验证了所提出方法的有效性与理论的正确性.
1 航天器动力学模型与控制问题描述为了避免奇异问题,考虑采用修正的罗德里格参数描述航天器姿态运动学与动力学方程[17]:
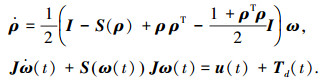
|
(1) |
式中:ρ∈R3为星体坐标系相对于惯性空间坐标系的修正的罗德里格参数;ω(t)∈R3为航天器本体坐标系相对地心惯性坐标系的旋转角速度在本体坐标系上的分量;J∈R3×3为航天器转动惯量;Td(t)∈R3为外部干扰;u(t)∈R3为作用在星体上的合控制力矩;此外, S(·)为反对称矩阵.
在实际的航天工程中,为保证航天器姿态控制系统的高可靠性,航天器执行机构的设计往往采用冗余配置情况,考虑图 1所示的正安装于航天器本体坐标系的理想安装结构.然而,在航天工程中,由于受安装技术的限制,航天器执行机构在不同程度上存在安装偏差.所谓安装偏差即是反作用飞轮在实际坐标系中安装的位置与本体坐标系中理想位置的偏差,如图 1所示.这里Δαi与Δβi(i=1, 2, 3, 4)定义为飞轮的安装偏差角.
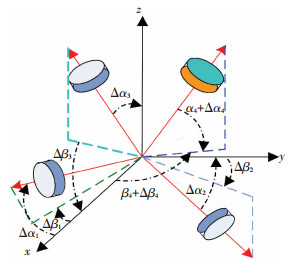
|
图 1 存在安装偏差反作用飞轮配置结构 |
根据图 1给出的反作用飞轮安装框图,可计算出反作用飞轮实际输出总力矩为u=(D+ΔD)τ.式中:
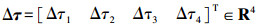
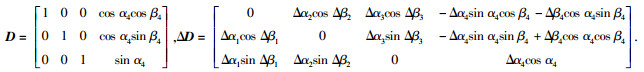
|
在航天器在轨运行过程中,由于执行机构要经常性地完成各种操作在轨,使得反作用飞轮时常发生故障;由此,同时考虑执行器存在故障与安装偏差意义下的航天器的动力学方程可修改为
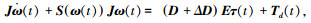
|
(2) |
这里E定义为E=diag(e1, e2, e3, e4), 式中ei为第i个反作用飞轮的有效因子,且满足0≤ei≤1(i=1, 2, 3, 4);当ei=1时,表明第i个反作用飞轮工作完好;当ei=0时,表明第i个反作用飞轮完全失效;当0<ei<1时,表明第i个反作用飞轮存在部分失效.
为了便于控制器设计,给出如下合理假设:
假设1 对于反作用飞轮的安装偏差角为小角度,也即安装偏差矩阵范数有界,由此存在一个较小的常数γ使得‖ΔD‖≤γ, 其中γ>0为未知常数.
假设2 对于E=diag(e1, e2, e3, e4)所描述的具有冗余反作用飞轮的故障形式,这里假设某个或某些反作用飞轮存在故障,但是失效后要求满足约束rank(DE)=3.
假设3 假设各个飞轮的特性相同,并且其最大输出力矩为τm,且满足幅值受限的要求‖τ(t)‖≤τm.
假设4 外部干扰Td(t)未知但满足有界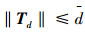
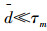
由此,本文的控制目标可以描述为:对于航天器系统(2),存在反作用飞轮故障、安装偏差、控制受限以及外部干扰的约束,满足上述假设1~4,且对于满足任意的物理意义的初始状态,设计控制律τ(t),使得闭环系统的状态稳定, 也即
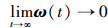
基于滑模控制方法设计的控制器主要分为:1)滑模面的选取;2)控制律的设计,并证明系统状态在任意初始位置有限时间到达滑模面和收敛到平衡点,从而保证了航天器状态最终稳定的特性.
2.1 积分滑模面设计基于航天器动力学模型式(1)的特性,选取如下积分滑模面
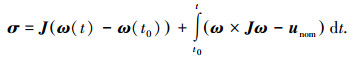
|
(3) |
式中:t0为系统的初始时刻;unom为航天器动力学标称系统的控制律;这里定义航天器动力学标称系统为忽略外部干扰等因素的一类航天器动力学系统,即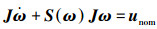
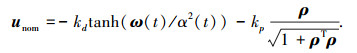
|
(4) |
式中:kp、kd分别为控制增益;α2(t)为非零的成型函数[16],且满足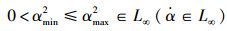
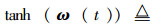
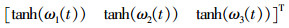
注1 由式(4)可知,通过调整控制参数kp与kd使得控制输出满足幅值受限,即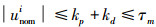
由滑模面式(3)可知,对其两端求时间导数可得
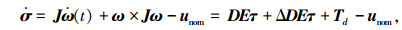
|
(5) |
由此,可得出如下定理.
定理1 针对存在外界干扰、安装偏差、飞轮故障以及控制受限的航天器姿态控制系统(2),满足假设1~4,采用式(3)的积分滑模面设计如下控制律:

|
(6) |
其中
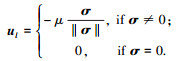
|
这里参数μ的选取满足如下约束:
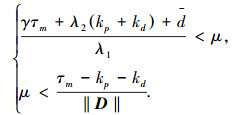
|
(7) |
这里定义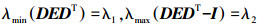
证明 设计Lyapunov函数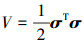
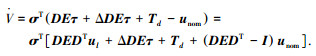
|
当σ≠0时,则有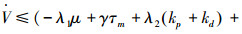

在积分滑模容错控制器设计过程中,由式(7)可知,其要求系统安装偏差矩阵、扰动以及故障的局部信息的上界应该是已知的.然而,在实际应用中,预先了解这些不确定项因素是很困难的,更不用说给出不确定性的明确范围.为解决该问题,本文提出一种自适应积分滑模控制器的设计方法.
设计如下控制律
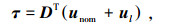
|
(8) |
其中
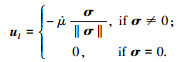
|
这里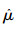
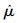
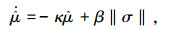
|
(9) |
其中κ, β>0为带设计的自适应因子.由此给出本文的第2个主要结论.
定理2 针对存在外界干扰、安装偏差、飞轮故障以及控制受限的航天器姿态控制系统(2),满足假设1~4,如果采用式(3)的积分滑模面,并设计式(8)的控制律与式(9)的自适应律,那么系统的滑动模态σ(t)=0是有界稳定的,且实现上述控制目标.
证明 选取Lyapunov函数
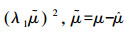
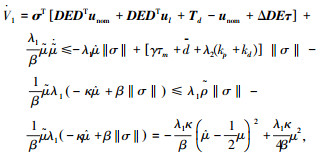
|
由此系统是有界稳定的.另外,对于自适应律式(9),为了确保自适应参数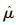
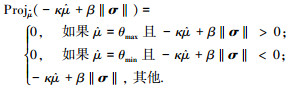
|
由此改进的自适应律为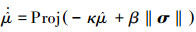
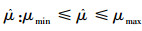
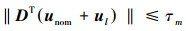
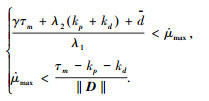
|
为了验证本文所设计控制器的有效性,利用MATLAB/SIMULINK软件,对航天器姿态机动过程进行数值仿真分析与研究, 如图 2~4所示.这里所采用的卫星参数为: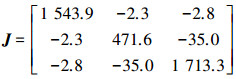
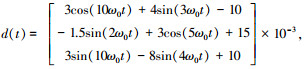
|
|
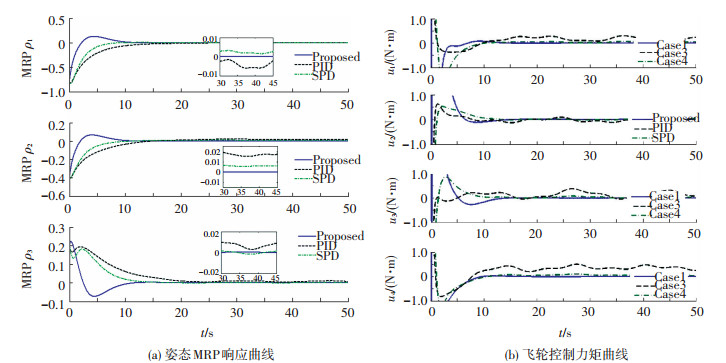
图 2 第1种情况的仿真结果 |
|
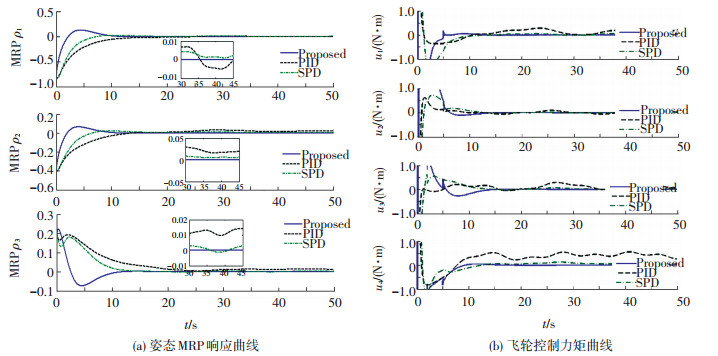
图 3 第2种情况的仿真结果 |
|
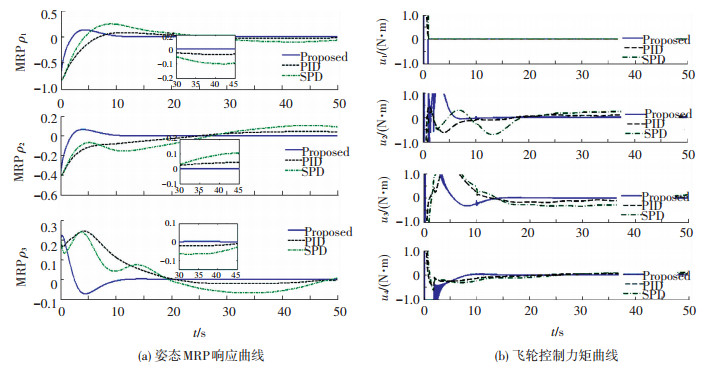
图 4 第3种情况的仿真结果 |
式中ω0=0.1/(rad·s-1),这里假设执行机构的输出力矩最大幅值为1 N·m.此外,反作用飞轮安装偏差角度为Δαi=[0.2 0.1 0.2 0.3],Δβi=[0.2 0.2 0.3 0.2].
为了验证方法的有效性,用如下3种工况情形进行仿真验证与比较.
1) 4个反作用飞轮工作正常(无故障发生).
2) 部分反作用飞轮存在故障(故障Ⅰ)为e1=1;e2=0.2, t>5;e3=0.4, t>2;e4=1.即:第1个飞轮工作正常;第2个飞轮在正常工作5 s后,存在部分失效,即其控制能力将损失80%;第3个飞轮在工作正常2 s后,同时也存在部分失效,即其控制能力将损失60%;第4个飞轮工作正常.
3) 部分飞轮存在故障,且某个飞轮彻底失效(故障Ⅱ)为e1=0, t>1;e2=0.8, t>3;e3=0.4, t>10;e4=0.2, t>2.即:第1个飞轮在工作1 s后,其彻底失效工作,其输出为0;第2个飞轮在工作3 s后,存在部分失效,其控制能力损失20%;第3个飞轮在工作10 s后,同时存在部分失效,其控制能力损失60%;第4个飞轮在工作2 s后,同时也存在部分失效,其控制能力损失80%.
另外,为了便于比较与分析,数值仿真过程中采用3种不同的控制方法:1)本文提出的自适应积分滑模容错控制(proposed);2)文献[13]提出的饱和比例-微分控制(SPD)方法;3)传统PID控制方案.
由上述仿真分析与比较,可知:
1) 由图 2仿真曲线可知,所采用的3种控制器均使得该系统是稳定的,但是文献[13]给出控制方法,使得系统存在稳态误差,也即对带有常值的干扰抑制能力比较差;而对于PID控制器,尽管引入积分项的作用,但是其控制器的设计并没有显式考虑控制受限的约束,而在仿真中采用硬饱和的方法,使得其也存在稳态误差.
2) 由图 3仿真曲线可知,所采用的3种控制器均可保证闭环系统是稳定的,但是对于PID控制,由于故障的影响,其呈现较大的震动;相当于文献[13]给出控制方法,尽管其对反作用飞轮构故障具有一定的容错能力,但是由于常值干扰的存在,其呈现稳态误差;对于本文说提出的控制方法,由于其对执行机构故障具很好容错能力,并且由于积分项与干扰抑制项的引入,其闭环控制系统的精度仍然满足系统要求.
3) 由图 4仿真曲线可知,PID控制下的系统已经失稳;对于文献[13]提出的控制算法能够保证系统是稳定的,但是存在震荡,且控制精度差;而对于提出的自适应积分滑模容错控制策略,其仍能保证系统稳定度的要求.
综上所述,针对存在执行机构故障、控制受限、外部干扰以及执行器安装偏差所约束下,所提出的自适应积分滑模容错控制器在能保证航天器控制系统稳定的要求,仿真研究验证了理论的有效性;然而,由上述的仿真结果,对于所设计的控制器,由于在控制开始阶段采用较大的控制幅值去实现系统稳定,使得系统在开始阶段存在姿态相应的幅值相当于其他两种方法较大一些,在后续研究中将进一步考虑系统的暂态相应的约束,进而实现高精度的姿态控制任务.
4 结论1) 该控制器显式的引入了饱和函数保证了执行器输出力矩的饱和约束,有效地避免了由于执行机构饱和对系统产生的不利影响.
2) 该控制方案在不需要执行器故障信息情况下能保证容错控制系统的渐近稳定性能,结构简单,便于工程实现.
3) 参数自适应技术的引入有效地减小了控制系统对一些不确定性上确界的依赖,增强了系统的鲁棒性能.此外,通过数值仿真对比,表明了本文鲁棒容错控制方案优越性,保证了闭环故障系统的高精度稳定.
| [1] |
XING G Q, PARVEZ S. Nonlinear attitude state tracking control for spacecraft[J]. Journal of Guidance, Control, and Dynamics, 2001, 24(3): 624-626. DOI:10.2514/2.4754 |
| [2] |
胡庆雷, 姜博严, 石忠. 基于新型终端滑模的航天器执行器故障容错控制[J]. 航空学报, 2014, 35(1): 249-258. |
| [3] |
KRISTIANSEN R, NICKLASSON P. Satellite attitude control by quaternion-based backstepping[J]. IEEE Transactions on Control Systems Technology, 2009, 17(1): 227-232. DOI:10.1109/TCST.2008.924576 |
| [4] |
张爱华, 胡庆雷, 霍星. 过驱动航天器自适应姿态补偿控制及控制分配[J]. 哈尔滨工业大学学报, 2014, 46(1): 18-22. |
| [5] |
HU Qinglei. Sliding mode maneuvering control and active vibration damping of three-axis stabilized flexible spacecraft with actuator dynamics[J]. Nonlinear Dynamics, 2008, 52(3): 227-248. DOI:10.1007/s11071-007-9274-6 |
| [6] |
BOSKOVIC J D, LI Saiming, MEHRA R K. Robust adaptive variable structure control of spacecraft under control input saturation[J]. Journal of Guidance, Control, and Dynamics, 2001, 24(1): 14-22. DOI:10.2514/2.4704 |
| [7] |
CAI Wenjun, XU Jianxin. Nonlinear, integral-type sliding surface for both matched and unmatched uncertain systems[J]. IEEE Transactions on Automatic Control, 2004, 49(8): 1355-1360. DOI:10.1109/TAC.2004.832658 |
| [8] |
HU Qinglei, ZHANG Youmin, HUO Xing, et al. Adaptive integral-type sliding mode control for spacecraft attitude maneuvering under actuator stuck failures[J]. Chinese Journal of Aeronautics, 2011, 24(1): 32-45. DOI:10.1016/S1000-9361(11)60005-8 |
| [9] |
JIANG Ye, HU Qinglei, MA Guangfu. Adaptive backstepping fault-tolerant control for flexible spacecraft with unknown bounded disturbances and actuator failures[J]. ISA Transactions, 2010, 49(1): 57-69. DOI:10.1016/j.isatra.2009.08.003 |
| [10] |
CAI Wenchuan, LIAO Xiaohong, SONG D Y. Indirect robust adaptive fault-tolerant control for attitude tracking of spacecraft[J]. Journal of Guidance, Control, and Dynamics, 2008, 31(5): 1456-1463. DOI:10.2514/1.31158 |
| [11] |
JIN J, KO S, RYOO C K. Fault tolerant control for satellites with four reaction wheels[J]. Control Engineering Practice, 2008, 16(10): 1250-1258. DOI:10.1016/j.conengprac.2008.02.001 |
| [12] |
HU Qinglei. Robust adaptive sliding-mode fault-tolerant control with L2 -gain performance for flexible spacecraft using redundant reaction wheels[J]. IET Control Theory & Applications, 2010, 4(6): 1055-1070. |
| [13] |
WALLSGROVE R J, AKELLA M R. Globally stabilizing saturated attitude control in the presence of bounded unknown disturbances[J]. Journal of Guidance, Control, and Dynamics, 2005, 28(5): 957-963. DOI:10.2514/1.9980 |
| [14] |
LIM H C, BANG H. Adaptive control for satellite formation flying under thrust misalignment[J]. Acta Astronautica, 2009, 65(1/2): 112-122. |
| [15] |
HU Qinglei, LI Bo, ZHANG Aihua. Robust finite-time control allocation in spacecraft attitude stabilization under actuator misalignment[J]. Nonlinear Dynamics, 2013, 73(1): 53-71. |
| [16] |
姜野, 胡庆雷, 马广富. 航天器时延自适应变结构容错控制[J]. 控制与决策, 2010, 25(5): 651-656. |
| [17] |
SIDI M J. Spacecraft dynamics and control[M]. Londom: Cambridge Univorsity Press, 1997.
|
| [18] |
HU Qinglei, LI Bo, ZHANG Youmin. Nonlinear proportional-derivative control incorporating closed-loop control allocation for spacecraft[J]. Journal of Guidance, Control, and Dynamics, 2014, 37(3): 799-812. DOI:10.2514/1.61815 |
| [19] |
IOANNOU P, SUN Jing. Robust adaptive control[M]. Englewood Cliffs, NJ: Prentice-Hall, 1996.
|
 2016, Vol. 48
2016, Vol. 48


