随着新世纪航天技术的发展,世界各国对空间资源的利用和支配已经成为未来太空竞争的发展趋势[1].航天器悬停控制是航天技术的重要发展方向之一.“悬停”是指伴随航天器与参考航天器在长时间内保持相对位置不变的状态.悬停技术在深空探测、非合作目标在轨服务、跟踪监视等领域具有广泛的应用[2-3].
最初关于悬停的研究大多是相对小天体的悬停技术[4].文献[5]设计了对小行星Castalia进行悬停控制的方法.文献[6]基于“无死区”的控制思路,对小行星悬停控制时的边界问题进行了研究.文献[7]提出利用电推进实现重力牵引航天器相对小行星的悬停.文献[8-9]对文献[7]的动力学方程和推进方法等进行了改进.近年来,追踪航天器相对于目标航天器的悬停技术具有了一定的研究结果.文献[2-3]分别设计了圆轨道下航天器相对于目标的正下方以及任意位置的开环悬停控制方法.文献[10-12]针对椭圆轨道任意位置悬停和共面悬停的开环控制算法进行了深入的研究.文献[13]采用LQR最优控制方法设计了航天器闭环悬停控制律.文献[14]基于误差递推模型设计考虑偏心率差异的控制律,实现了共面轨道内的编队悬停控制.文献[15]提出了基于θ-D非线性寻优算法的悬停控制律.但是上述文献普遍存在的问题是:1)开环定点悬停控制方法对初始状态误差比较敏感,对摄动力等干扰的鲁棒性较差,而且控制误差会随时间积累,甚至无法维持悬停;2)目前已有的悬停闭环控制方法通常实现的是使悬停误差渐近收敛的过程,并且在存在干扰时,悬停的精度无法得到保证.近年来,有限时间控制问题引起了广泛的关注.相比于渐近稳定控制,有限时间控制能在有限时间内使系统达到稳定,并且通常具有更好的鲁棒性和抗扰动性(关于有限时间控制的详细介绍,可以详见文献[16]).其中文献[17]基于固定时间稳定的概念,给出了一种新型的有限时间控制算法,可以不依赖于系统初始状态,预先确定收敛时间.
针对上述问题,受文献[17]的启发,本文基于固定时间稳定理论设计了相对空间目标的闭环悬停控制律.在存在初始悬停误差和干扰的情况下能在有限时间内达到悬停控制的目的.可以通过调节干扰上界γ0,收敛域半径r和到达时间Tmax这3个参数实现长时间、高精度定点悬停.通过充足的仿真算例验证了本文算法的有效性.
1 动力学模型 1.1 轨道坐标系定义轨道坐标系是指:原点位于航天器质心;x轴沿地心指向航天器方向;y轴在轨道平面内与x轴垂直,指向速度方向;z轴垂直于轨道平面,与x、y轴组成右手坐标系.
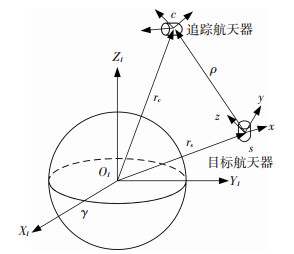
1.2 相对轨道动力学模型记目标航天器为s,追踪航天器为c.取建立在s上的轨道坐标系作为相对运动坐标系,c与s的相对位置关系如图 1所示,其中OI-XIYIZI为地球惯性坐标系.
|
图 1 追踪航天器与目标航天器的相对位置关系 |
当s运行在近圆轨道上,且c与s距离较近时,c在s的轨道坐标系中的相对运动可近似由C-W方程(又称Hill方程)表示:
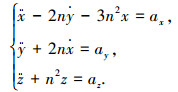
|
(1) |
式中: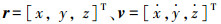
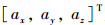
当不考虑摄动力和控制力,即式(1)右边全为0时,式(1)为齐次微分方程组,可求得c相对s的位置r与速度v为

|
其中
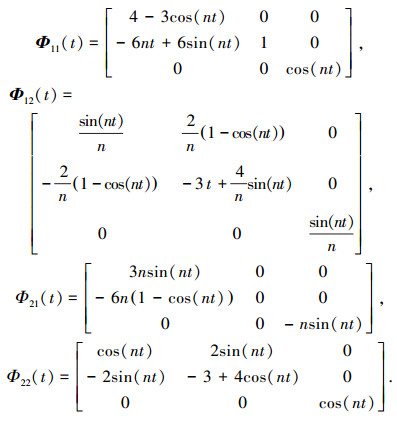
|
文献[17]基于固定时间稳定的概念,给出了一种新型的有限时间控制算法,可以不依赖于系统初始状态,预先确定收敛时间,以下概括给出该算法的关键步骤和结论.
考虑如下存在不确定性的系统:
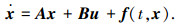
|
(2) |
式中:x∈Rn为状态量;u∈Rm为控制量;函数f:R+×Rn→Rn用来描述系统的不确定性.假设式(2)满足以下条件:1)矩阵对(A, B)能控;2)f(t, x)满足匹配条件f(t, x) = Bγ(t, x),且‖γ(t, x)‖ ≤ γ0(t, x).并定义Br = {x∈Rn:‖x‖∞≤ r}为系统状态的目标收敛域.
根据文献[18],可通过变换y = Gx将原系统化为如下分块形式:
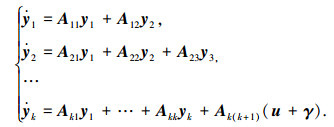
|
(3) |
式中: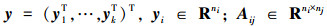
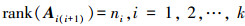
由于rank(Ai(i+1))=ni,从而有广义逆矩阵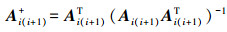
对式(3)进行非线性变换s=Φ(y),其中s=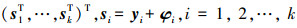
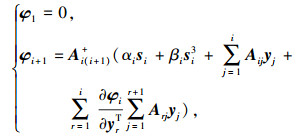
|
(4) |
其中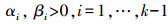
式(3)等价于
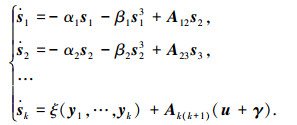
|
其中
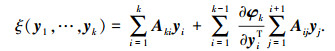
|
对于式(3),将控制律设计成如下形式:
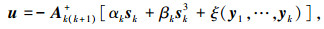
|
(5) |
令ε, Tmax为正实数,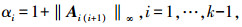
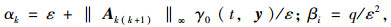
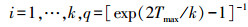
定义n-1次多项式的集合为Pn,可证明在式(5)的所有条件满足时,存在具有非负系数的多项式序列pi∈Pi,使得对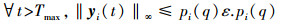

|
(6) |
为了进一步得到原系统(2)的稳定性,令
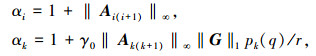
|
(7) |
其中r>0,i=1, …, k-1.
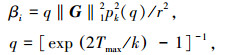
|
(8) |
式中r,Tmax>0,i=1, …, k.进一步可以得到闭环系统状态在时间Tmax内收敛到目标域Br内[17].
2.2 悬停控制律设计首先由C-W方程式(1),令状态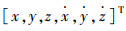
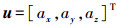
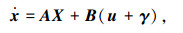
|
(9) |
其中
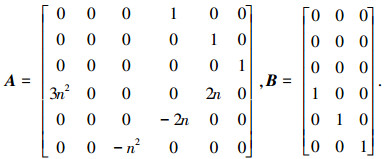
|
根据悬停的要求,令期望状态Xd=
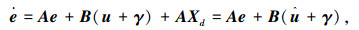
|
(10) |
式中
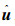
可以发现,式(10)直接满足式(3)的形式,令y1由e中前3个分量组成,y2由e中后3个分量组成,有
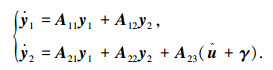
|
(11) |
其中
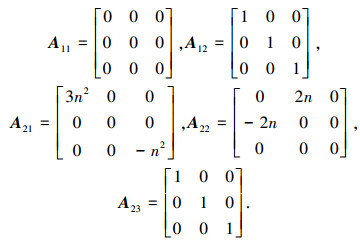
|
基于固定时间稳定控制算法的固定时间稳定基础和悬停控制对象相关模型(9)~(11),本文给出如下形式的固定时间稳定悬停控制律为
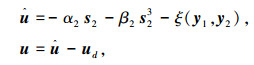
|
(12) |
式中α2, β2, s2以及ξ(y1, y2)的定义如式(13)~(17)所示.
定理1 对式(1)描述的相对轨道模型系统,在式(12)描述的控制律作用下,可以实现相对期望状态Xd的悬停控制,且悬停误差满足固定时间稳定.
证明 将式(11)中的模型参数矩阵A11和A12带入式(6),可得
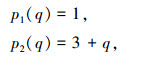
|
(13) |
取控制参数r,Tmax,γ0>0,根据式(7)~ (8)得到相应系数:
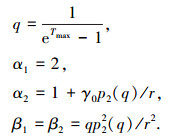
|
(14) |
结合式(14)求得的参数,进行式(4)所示的非线性变换,可以得到
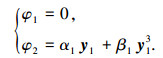
|
(15) |
进一步,可以得到式(11)的等价系统:
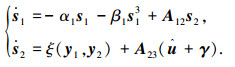
|
(16) |
其中
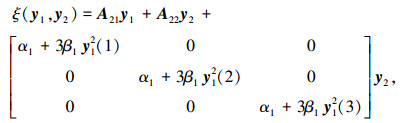
|
(17) |
式中yi(j)为yi中第j个元素.
将式(13)~(17)代入式(5),即可求得固定时间稳定悬停控制律(12),根据固定时间稳定控制算法的固定时间稳定基础,可以得到控制律(12),即可以保证系统(9)的悬停误差e是固定时间稳定的,因此得到系统(1)的固定时间稳定闭环悬停控制律.其中3个控制参数都有明确的物理意义,可根据实际控制需求进行调节:干扰上界γ0与空间摄动加速度大小有关;收敛域半径r与稳定后的悬停精度有关;到达时间Tmax预估达到稳定状态的过渡过程时间.
3 仿真算例 3.1 仿真参数设目标航天器处于600 km的太阳同步轨道,初始轨道根数为:半长轴a= 6 978 140 m,偏心率e= 0,轨道倾角i= 97.759 7°,升交点赤经Ω= 0,近地点幅角ω=0,真近点角f=0;追踪航天器悬停于目标左后下方,期望状态Xd= [-1 000 m, -100 m, 100 m, 0 m/s, 0 m/s, 0 m/s]T.为了便于仿真观察,假设追踪航天器由具有一定轨道倾角差的较低轨道已经自由运动到悬停位置,但具有一定的初始速度误差,选取初始状态为X0= [-1 000 m, -100 m, 100 m, 0 m/s, 0.54 m/s, 0 m/s]T.
控制律(12)的控制参数选取为Tmax=20,r=1,γ0=0.02.假设单轴最大控制加速度分量amax=0.1 m/s2,当某一坐标轴控制加速度分量大于amax时,取u = amax (u*/|u*|),u*为指令加速度.仿真时加入的轨道摄动包括:地球非球形摄动、大气摄动、太阳光压摄动和日月引力摄动等.
3.2 与PID悬停控制律对比仿真分析悬停控制时间为目标航天器一个轨道周期的仿真结果, 如图 2~5所示.
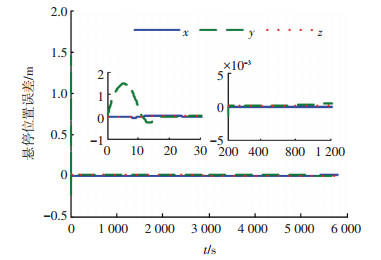
|
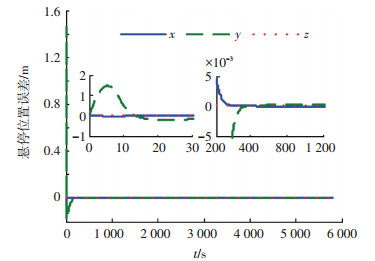
图 2 控制律(12)作用下悬停位置误差变化曲线 |
|
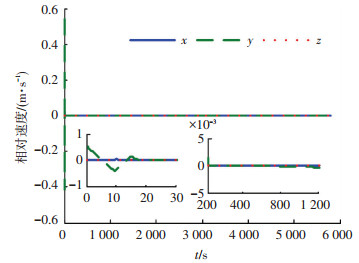
图 3 PID控制律作用下悬停位置误差变化曲线 |
|
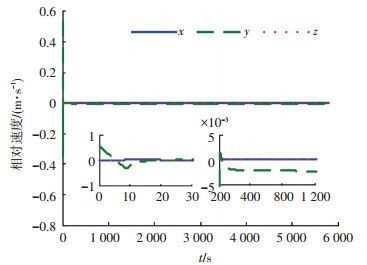
图 4 控制律(12)作用下相对速度变化曲线 |
|
图 5 PID控制律作用下相对速度变化曲线 |
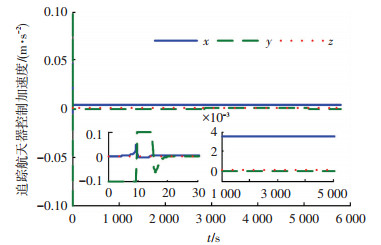
从图 2可以看出,在控制律(12)作用下,经过20 s左右的过渡过程,追踪航天器即可进入并保持在悬停稳定状态,且悬停误差在±5×10-3 m以内,表明控制律(12)具有较好的悬停控制精度.从图 3可以看出,在PID控制律作用下,需要200 s左右的时间才可以达到±5×10-3 m的悬停精度,因此过渡过程所需的时间远大于控制律(12)情况.通过图 4,5的对比,可以看出,在控制律(12)作用下,进入悬停稳定状态时的相对速度远小于PID控制律情况,因此表明控制律(12)具有较好的悬停控制稳定度.图 6,7分别是在控制律(12)作用下追踪航天器的控制加速度曲线和所对应的速度增量曲线,可以看出在整个悬停控制过程中控制加速度可以维持在4×10-3 m/s2以内,速度增量可以维持在20 m/s以内,表明控制律(12)具有较低的燃料消耗.
|
图 6 控制律(12)作用下追踪航天器控制加速度变化曲线 |
|
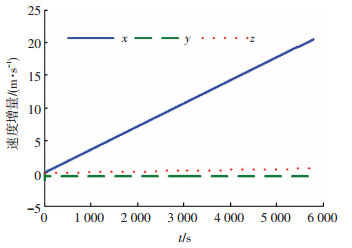
图 7 控制律(12)作用下控制加速度产生的速度增量变化曲线 |
图 6表明,控制律(12)在过渡过程中需要较大的控制加速度,悬停稳定后各轴控制加速度分量为常值,与文献[3]中给出的开环控制期间推力变化情况一致.图 7表明,控制律(12)一个轨道周期的悬停所需速度增量方面:x方向为20.45 m/s;y方向为-0.54 m/s;z方向为0.68 m/s.
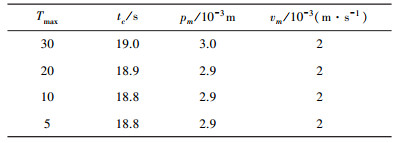
3.3 控制参数选取分析以下给出控制律(12)的控制参数选取的分析.其中控制律(12)的控制参数的标称值为Tmax=20,r=1,γ0= 0.02,表 1~3分别给出当其中一个控制参数变化,另外两个控制参数不变情况下的控制性能.被统计的控制性能包括收敛时间tc、悬停精度(一个轨道周期内的相对位置误差幅值) pm和悬停稳定度(一个轨道周期内的相对速度误差幅值) vm.
| 表 1 Tmax变化时的控制性能情况 |
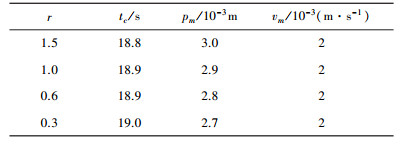
| 表 2 r变化时的控制性能情况 |
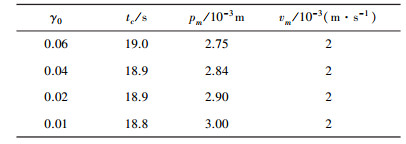
| 表 3 γ0变化时的控制性能情况 |
通过表 1可以看出,当Tmax逐渐减小时,tc和pm有逐渐减小的趋势,vm保持不变.通过表 2可以看出,当r逐渐减小时,tc有逐渐增大的趋势,pm有逐渐减小的趋势,vm保持不变.通过表 3可以看出,当γ0逐渐减小时,tc有逐渐减小的趋势,pm有逐渐增大的趋势,vm保持不变.通过对表 1~3的分析,可以得出:1)为了达到减小收敛时间的目的,可以通过缩小Tmax和γ0,增大r的方式实现; 2)为了达到提高悬停精度的目的,可以通过缩小Tmax和r,增大γ0的方式实现; 3)通过调整Tmax、r和γ0等控制参数,一般对悬停稳定度影响不大.
4 结论1) 本文基于固定时间稳定理论,设计了一种闭环悬停控制律.通过调节干扰上界γ0,收敛域半径r和到达时间Tmax这3个参数来适应不同的控制需求,能够有效地解决开环控制律的误差发散问题和常规闭环控制律的响应速度较慢问题.
2) 对初始状态误差和摄动干扰等具有较好的鲁棒性.能够在有限时间内让闭环系统快速进入悬停误差收敛状态,实现长时间、高精度定点悬停.
| [1] |
袁建平, 朱战霞. 空间操作与非开普勒运动[J]. 宇航学报, 2009, 30(1): 42-46. |
| [2] |
林来兴, 黎康. 卫星对空间目标悬停的轨道动力学与控制方法研究[J]. 中国空间科学技术, 2008, 28(1): 9-12. |
| [3] |
闫野. 卫星相对空间目标任意位置悬停的方法研究[J]. 中国空间科学技术, 2009, 29(1): 1-5. |
| [4] |
BROSCHART S B, SCHEERES D J. Control of hovering spacecraft near small bodies:application to asteroid 25143 itokawa[J]. Journal of Guidance, Control, and Dynamics, 2005, 28(2): 343-354. DOI:10.2514/1.3890 |
| [5] |
SAWAI S, SCHEERES D J, BROSCHART S B. Control of hovering spacecraft using altimetry[J]. Journal of Guidance Control and Dynamics, 2002, 25(4): 786-795. DOI:10.2514/2.4947 |
| [6] |
BROSCHART S B, SCHEERES D J. Boundedness of spacecraft hovering under dead-band control in time-invariant systems[J]. Journal of Guidance Control and Dynamics, 2007, 30(2): 601-610. DOI:10.2514/1.20179 |
| [7] |
LU E T, LOVE S G. A Gravitational tractor for towing asteroids[J]. Nature, 2005, 438(11): 177-178. |
| [8] |
WIE Bong. Dynamics and control of gravity tractor spacecraft for asteroid deflection[J]. Journal of Guidance Control and Dynamics, 2008, 31(5): 1413-1423. DOI:10.2514/1.32735 |
| [9] |
WIE Bong. Hovering control of a solar sail gravity tractor spacecraft for asteroid deflection[C]//Proceedings of the 2007 Planetary Defense Conference. Washington, D. C: IEEE, 2007: 145-150.
|
| [10] |
闫野, 朱亚文. 非圆轨道卫星实现共面悬停的方法[J]. 中国空间科学技术, 2010(2): 42-48. |
| [11] |
朱亚文, 闫野. 椭圆轨道卫星空间任意位置悬停的方法[J]. 中国空间科学技术, 2010(6): 17-23. |
| [12] |
王功波, 孟云鹤, 郑伟, 等. 基于轨道动力学的椭圆轨道悬停方法[J]. 宇航学报, 2010(6): 1527-1532. |
| [13] |
薛白, 佘志坤, 余婧, 等. 基于混杂系统的空间飞行器悬停控制[J]. 中国空间科学技术, 2010(2): 61-67. |
| [14] |
段广仁, 谭峰, 张世杰, 等. 卫星轨迹跟踪控制的参数化方法[J]. 空间控制技术与应用, 2008, 34(5): 3-7. |
| [15] |
付艳明, 李伟, 段广仁. 基于T-H方程的卫星轨迹模型参考输出跟踪控制方法[J]. 宇航学报, 2013, 34(4): 496-502. |
| [16] |
丁世宏, 李世华. 有限时间控制问题综述[J]. 控制与决策, 2011, 26(2): 161-169. |
| [17] |
POLYAKOV A. Nonlinear feedback design for fixed-time stabilization of linear control systems[J]. IEEE Transactions on Automatic Control, 2012, 57(8): 2106-2110. DOI:10.1109/TAC.2011.2179869 |
| [18] |
DRAKUNOV S V, IZOSIMOV D B, LUKYANOV A G. The block control principle[J]. Automation and Remote Control, 1990, 51(5): 601-608. |
 2016, Vol. 48
2016, Vol. 48