桁架是一种高效、灵活的结构形式,桁架杆件主要受轴向力作用,使用碳纤维轴向分布的复合材料杆件可很好地发挥碳纤维力学性能优势,同时改善桁架振动特性,提高结构空间环境适应性[1].目前常采用金属接头连接复合材料杆件,金属接头复合材料桁架研究也比较多.但是金属接头质量大,连接界面热稳定性差,连接处还会产生电偶腐蚀现象[2-3],为提高结构性能,近年来开始逐渐应用复合材料接头连接的全复合材料桁架[4-5].接头是影响复合材料桁架承载性能的关键,复合材料接头材料属性复杂,其力学性能和成型工艺密切相关,针对金属接头连接的复合材料桁架相关研究成果并不能直接应用于全复合材料桁架,目前对全碳纤维复合材料桁架的研究还比较少[6].固有频率及阻尼强弱是结构重要承载性能指标,而常用的狭长梁式桁架固有频率较低,易发生动力破坏[7],因此有必要掌握此类桁架的模态及阻尼特性.
针对复合材料桁架振动特性,陶国权等[8]采用锤击法,施加弹性悬挂约束,对金属接头复合材料桁架进行自然脉动实验.冯鹏等[9]将加速度传感器固定在结构振动反应最大的位置,对复合材料桁架桥进行振动测试.BAI等[10]针对全复合材料人行桥冲击和人致振动两种工况,在结构激励未知的情况下,均采用峰值拾取法和随机子空间识别法提取结构振动参数,结果表明这两种方法对全复合材料人行桥的实际使用状态均适用.针对狭长梁式各向同性材料桁架,Noor等[11]基于能量互等原理将桁架等效为梁,利用等效得到的等效梁刚度及质量参数,快速有效地计算桁架模态.刘福寿等[12]基于该思想,对环形碳纤维复合材料桁架结构进行了动力学建模与分析.Sailhian等[13]基于上述思想,利用哈密顿原理建立等效梁的运动控制方程,进而分析桁架的动力学特性,相关结论得到了实验验证.针对纤维增强复合材料结构的阻尼特性,Adams等[14]从宏观角度出发,提出模态应变能阻尼模型,该模型定义结构阻尼为一个应力循环过程中耗散的能量与储存的最大应变能之比.YANG等[15]基于该模型,计算了碳纤维金字塔桁架夹芯板的阻尼损耗因子,并通过实验验证.目前针对梁式全碳纤维复合材料桁架的研究还很少,尤其缺少实验之外的表征方法研究,本文从实验、仿真及理论分析等出发,分析了梁式全碳纤维复合材料桁架的模态及阻尼特性,得到其有效表征方法.
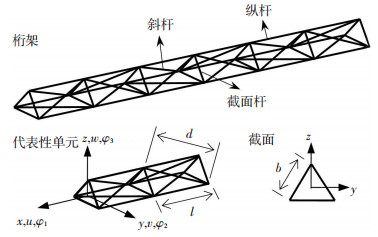
1 振动实验实验桁架如图 1所示,杆件由拉挤工艺制备,先后经过薄壳胶接、纤维束缠绕及模压固化实现杆件连接,具体工艺过程见文献[16].原材料为T700/TDE-85.杆件长度l、b、d分别为500、260、563 mm;纵杆、截面杆及斜杆均为空心圆管,截面外径分别为20.0、16.0、16.0 mm,壁厚分别为2.25、2.00、2.00 mm.接头厚2.0 mm,质量均为60 g.
|
图 1 实验桁架示意 |
采用锤击法测试桁架的模态和阻尼参数,通过力传感器获取激励力谱,通过三轴加速度传感器采集加速度信号,采集并分析实验数据得到频响函数,经计算机处理得到桁架模态函数.本实验采用KISTLE9724A5000冲击锤(力传感器和锤帽)对桁架进行激励,使用PCB356A25三轴加速度传感器采集桁架振动数据,其他实验硬件包括AVANT一体式数据采集与分析仪、MESCOPE模态分析后处理软件.具体实验方案如图 2所示.

|
图 2 实验方案示意 |
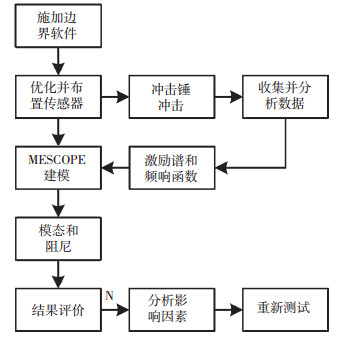
实验基本流程如图 3所示.首先,根据结构特点把桁架离散为若干节点,以代替连续系统,并对节点编号,同时在MESCOPE建模时,保证坐标系及节点编号与实际情况一致;测量时要注意加速度传感器的方向,频响矩阵中必要数据必须存在;此外,为使测试针对桁架整体振动,避免出现单杆振动的情况,采用传感器位置和激励点位置优化理论,确定测点为桁架所有节点,加速度传感器布置位置如图 2所示.实验主要针对桁架竖向弯曲振动,实验对象及装置如图 4所示.桁架由两个等高刚性平台支撑,两端由螺栓及木制模具提供简支约束.实验时,使用冲击锤对所有测点冲击3次,并取平均值,得到激励力谱和频响函数.根据桁架真实构形及尺寸,在MESCOPE软件中建模.然后输入实验获得的激励力谱和频响函数结果文件,处理得到桁架固有频率及对应振型和阻尼.最后采用模态置信准则指标衡量模态之间的相似度,进而评估实验结果好坏.
|
图 3 实验基本流程 |

|
图 4 实验对象及装置 |
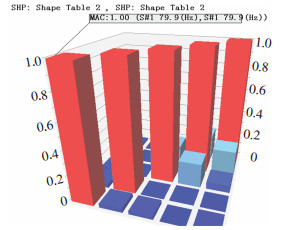
采用模态置信准则指标衡量模态之间的相似度,好的模态实验结果要求对角线位置为1,非对角线位置(模态参数相互之间影响)为0,如图 5所示.由图 5可知,本实验所得前5阶模态参数相互之间影响很小,模态实验结果可信.
|
图 5 实验所得前5阶模态置信准则指标 |
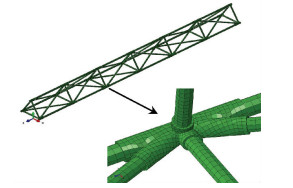
由于实验耗费较大,借助商业有限元软件进行仿真是复合材料结构分析的常用手段,一个兼顾分析精度和效率的仿真模型能够极大地方便结构的分析和设计.本文首先利用ABAQUS12.0中的模态分析模块,针对上述实验桁架进行模态仿真,得到桁架的振型和相应频率.之后为求解梁式全碳纤维复合材料桁架的结构阻尼损耗因子,提出采用模态应变能阻尼模型处理模态仿真结果数据得到结构阻尼损耗因子的方法.所提出的基于桁架模态仿真结果的桁架结构阻尼损耗因子计算方法,所依据的仿真结果数据为有限元模型所有单元的三维应力、应变值,因此仿真需要采用三维实体单元模型.有限元模态仿真所得单元应力、应变结果必须具有较高精度,这样才能保证接下来计算得到的结构阻尼损耗因子满足精度要求,同时桁架模态仿真建模需要控制单元数量,以减少软件求解和后续数据处理成本.为此,选择二次六面体减缩积分单元C3D20R,并配合少量二次完全积分楔形单元C3D8,以适应接头复杂构形的网格划分,这里采用减缩积分形式能够在不降低仿真精度的情况下显著降低计算成本,两类单元划分数量分别为40 658和1 836.实验桁架杆件和接头通过共固化过程实现连接,在仿真建模过程中,将它们之间的连接简化为绑定约束,即连接处从面节点位移值完全依赖主面上相应节点,建模时将连接界面接头一侧设置为主面,杆件一侧设置为从面.实验桁架有限元网格模型如图 6所示,按照表 1赋予该模型材料属性,具体通过ABAQUS软件的复合材料铺层功能实现.固定桁架一端底部节点在3个方向上的位移,以及另一端底部节点在竖向和横向的位移,以模拟简支边界条件.设置线性摄动频率提取分析步,具体采用子空间法求解.
|
图 6 实验桁架实体单元有限元模型网格划分 |
| 表 1 T700/TDE-85单向复合材料力学性能 |
文献[12]从宏观角度定义结构阻尼为一个应力循环过程中耗散的能量与储存的最大应变能之比,即模态应变能阻尼模型,该模型已被广泛应用于结构阻尼分析,这里引入该模型建立梁式全碳纤维复合材料桁架阻尼特性表征方法.上述桁架模态仿真结果包含所有单元的三维应力、应变值,因此容易想到利用模态应变能阻尼模型计算该桁架的结构阻尼损耗因子,即

|
(1) |
式中:1, 2, 3代表材料主方向,其中1为纤维方向;ηij为与材料主方向对应的材料阻尼损耗因子;Uijk为第k个单元对应于σij的应变能,表达式如下(单元内纤维方向相同)

|
(2) |
因此,计算结构阻尼损耗因子时,需要提前确定材料阻尼损耗因子ηij,然后采用实体单元有限元模型进行结构模态仿真,最后在后处理模块提取所有单元的应力、应变分量数据,按照式(1),(2)处理这些数据,得到结构阻尼损耗因子.
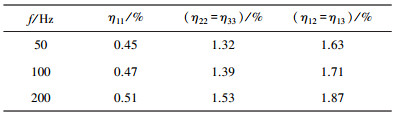
η11、η22可分别通过0°、90°铺层梁的实测结构阻尼损耗因子值,结合该梁的模态有限元分析结果数据,根据式(1)(i, j=1, 2)求解得到,η12则基于任意斜角度铺层梁经同样方法得到.由于单向碳纤维复合材料为横观各向同性,因此η13=η12、η33=η22,对于薄壁结构,可忽略η23的影响[13].针对本文实验桁架材料T700/TDE-85,采用0.1 mm厚T700/TDE-85预浸料(哈尔滨玻璃钢研究院提供)制备层合复合材料梁,采用上述锤击法测试其悬臂梁式边界条件下的结构阻尼损耗因子,同时针对相同工况进行模态有限元分析,按照上述思路,求得材料阻尼损耗因子(表 2).计算结构阻尼损耗因子时,对该数据进行线性拟合,得到与结构固有频率对应的材料阻尼损耗因子取值.
| 表 2 T700/TDE-85阻尼损耗因子 |
本文模态仿真及后续结构阻尼损耗因子计算针对只有3个代表性单元的实验桁架,但分析成本依然较大.实际应用中,梁式全碳纤维复合材料桁架尺度通常较大,并由基本桁架模块组成整体结构(如临近空间飞艇骨架结构),结构规模较大,因此,分析方法需要具有较高效率.针对狭长梁式桁架,文献[9]基于能量互等的等效原则,将离散桁架等效为连续梁,从而简化桁架线性动力学分析过程.该过程从桁架和等效梁能量相等的角度出发,推导等效梁的刚度及质量参数,进而计算等效梁的振动模态,并视其为桁架模态,从而提高桁架模态计算效率.其分析针对各向同性材料桁架,而本文为各向异性材料桁架,并且节点为刚性,并非严格意义上的“桁架”.考虑到刚节点导致的杆端弯矩有限,对杆件轴向受力状态影响不大,同时拉挤杆轴向受力状态使得与轴向垂直的两个材料主方向的材料参数对桁架振动模态影响有限.因此,为提高本文桁架模态分析效率,采用等效梁理论,假设截面位移为线性,并将空间应变分量泰勒展开至出现中心线变形量的二阶导数项,推导得到等效梁刚度和相应的质量密度参数分别如式(3)所示,然后根据该等效参数分析桁架模态.当然,该方法针对梁式全碳纤维复合材料桁架的适用性最终需由其他方法进行验证.
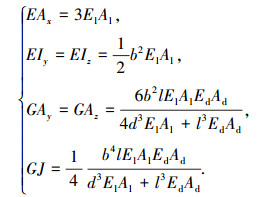
|
(3) |
式中:b、d分别为桁架截面杆、斜杆的长度; El、Al分别为纵杆轴向模量和截面积; Ed、Ad分别为斜杆轴向模量和截面积.

|
(4) |
式中:msum为桁架代表性单元总质量; Ab为截面杆截面积; ρl、ρb、ρd分别为纵杆、截面杆和斜杆的体密度,具体如图 1所示.
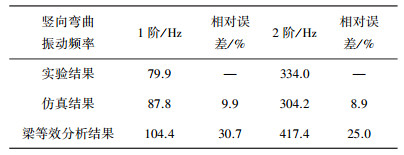
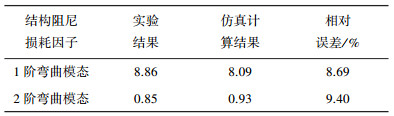
4 讨论梁式全碳纤维复合材料桁架两端简支约束时,竖向弯曲振动固有频率分析结果见表 3,前两阶振型分别如图 7、8所示,前两阶模态对应的结构阻尼损耗因子的实验及仿真计算值见表 4.

|
图 7 桁架1阶弯曲振型 |
|
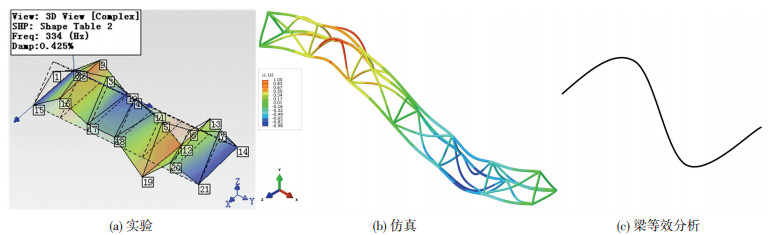
图 8 桁架2阶弯曲振型 |
| 表 3 固有频率分析结果 |
| 表 4 结构阻尼损耗因子的实验及仿真计算值 |
表 3表明,针对只包含3个代表性单元的梁式全碳纤维复合材料桁架,仿真得到的1、2阶弯曲振动频率误差在10%以内,精度较高,而梁等效分析相应误差却在30%左右,误差较大;图 7、8表明3种方法得到的桁架竖向弯曲振型是一致的.由此可知,上述基于实体单元有限元模型的模态仿真结果能够满足工程精度要求,模态仿真与实验结果还存在一定的差异,原因主要包括仿真时边界条件的近似误差、材料及工艺参数的建模误差,以及软件的系统误差.梁等效分析误差明显较大,这主要因为等效对象所含代表性单元数量较少.通过能量互等建立的梁等效分析本质上是一种均匀化方法,代表性单元数量越多,其等效精度越高.具体来看,简支边界约束条件下,桁架底部两端的接头质量和截面杆质量对桁架振动频率并没有影响,而梁等效分析考虑了该质量,当代表性单元只有3个时,这种差异对基频结果影响会比较明显;与等效梁轴向垂直的各方向(即横向)具有相同的抗弯刚度,而桁架各横向(包括竖向)抗弯刚度并不同,等效梁抗弯刚度为桁架各横向抗弯刚度的平均值,当代表性单元较少时,等效梁抗弯刚度与桁架竖向抗弯刚度相对差异明显;此外,梁等效分析误差原因同样包括造成上述仿真误差的工艺离散性,接头复杂性以及边界条件不一致等实验误差因素.
由表 4知,针对梁式全碳纤维复合材料桁架1、2阶竖向弯曲模态对应的结构阻尼损耗因子,仿真计算误差在10%以内.由于桁架结构阻尼计算过程包括原材料阻尼损耗因子的测定、结构模态仿真及数据后处理,并且测定原材料阻尼损耗因子同样需要进行仿真和数据处理,这一繁琐过程的累计误差在10%以内,表明上述结构阻尼仿真计算方法是可靠的.桁架结构阻尼损耗因子计算值和实验值之差,来源于贯穿上述过程的实验对象制备工艺离散性、实验过程操作误差、实验仪器的系统误差以及仿真误差、数据处理误差,此外还包括模态应变能阻尼模型本身的近似性.
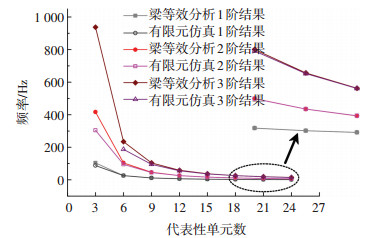
针对实验桁架代表性单元较少,不足以验证等效梁方法适用性这一问题.利用已证明具有较高精度的实体单元模态仿真方法,对包含更多代表性单元的梁式全碳纤维复合材料桁架进行模态仿真,并将梁等效分析结果与仿真结果进行比较,结果如图 9所示.由图 9可知,随着代表性单元数量的增加,两种结果相对差异迅速减小,当代表性单元数量大于18,二者差距小于1%.因此,利用梁等效理论分析大尺度梁式全碳纤维复合材料桁架模态特性,结果具有较高精度.梁等效理论可直接套用公式,这将方便大尺度碳纤维复合材料桁架结构的初步设计.
|
图 9 竖向弯曲频率的梁等效分析及有限元仿真结果 |
1) 针对梁式全碳纤维复合材料桁架模态及阻尼特性,上述基于实体单元有限元模型的模态仿真方法能够满足工程精度要求,根据模态仿真结果并采用模态应变能阻尼模型所建立的结构阻尼损耗因子仿真计算方法,误差在10%以内,该方法有效.
2) 当代表性单元数量大于18,梁等效理论分析所得频率与相应仿真结果差距小于1%,梁等效理论可用于大尺度梁式全碳纤维复合材料桁架模态的快速分析,这对于整体结构系统初步设计具有很重要的实用意义.本文所述锤击法振动实验方案能够较准确地测得梁式全碳纤维复合材料桁架模态及阻尼参数.
| [1] |
JU Su, SHENOI R A, JIANG Dazhi, et al. Multi-parameter optimization of lightweight composite triangular truss structure based on response surface methodology[J]. Composite Structures, 2013, 97: 107-116. DOI:10.1016/j.compstruct.2012.10.025 |
| [2] |
HOLLAWAY L C. Polymers, fibres, composites and the civil engineering environment:a personal experience[J]. International Journal of Advanced Structural Engineering, 2010, 13(5): 927-960. DOI:10.1260/1369-4332.13.5.927 |
| [3] |
BAI Yu, YANG Xiao. Novel joint for assembly of all-composite space truss structures:conceptual design and preliminary study[J]. Journal of Composites for Construction, 2013, 17(1): 130-138. DOI:10.1061/(ASCE)CC.1943-5614.0000304 |
| [4] |
鞠苏. 复合材料桁架弯曲特性与非线性约束优化设计[D]. 长沙: 国防科技大学, 2011.
|
| [5] |
WEAVER T J, TENSEN D W. Mechanical characterization of a graphite/epoxy isotruss[J]. Journal of Aerospace Engineering, 2000, 13(1): 23-35. DOI:10.1061/(ASCE)0893-1321(2000)13:1(23) |
| [6] |
POLYZOIS D J, RAFTOYIANNIS I G, OCHONSKI A. Experimental and analytical study of latticed structures made from FRP composite materials[J]. Composite Structures, 2013, 97(3): 165-175. |
| [7] |
YANG Jinshui, XIONG Jian, MA Li, et al. Vibration and damping characteristics of hybrid Carbon fiber composite pyramidal truss sandwich panels with viscoelastic layers[J]. Composite Structures, 2013, 106: 570-580. DOI:10.1016/j.compstruct.2013.07.015 |
| [8] |
陶国权, 卫宇晨, 吕明云, 等. 大型碳纤维桁架结构模态试验及特性[J]. 北京航空航天大学学报, 2011, 37(3): 316-319. |
| [9] |
冯鹏, 田野, 覃兆平. 纤维增强复合材料拉挤型材桁架桥静动力性能研究[J]. 工业建筑, 2013, 43(6): 36-41. |
| [10] |
BAI Yu, KELLER T. Modal parameter identification for a GFRP pedestrian bridge[J]. Composite Structure, 2008, 82(1): 90-100. DOI:10.1016/j.compstruct.2006.12.008 |
| [11] |
NOOR A K, ANDERSON M S, GREEN W H. Continuum models for beam and platelike lattice structures[J]. AIAA Journal, 1978, 16(12): 1219-1228. DOI:10.2514/3.61036 |
| [12] |
刘福寿, 金栋平, 陈辉. 环形桁架结构动力分析的等效力学模型[J]. 振动工程学报, 2013, 26(4): 516-521. |
| [13] |
SALEHIAN A, INMAN D J. Dynamic analysis of a lattice structure by homogenization:experimental validation[J]. Journal of Sound and Vibration, 2008, 316(1/2/3/4/5): 180-197. |
| [14] |
NI R G, ADAMS R D. The damping and dynamic moduli of symmetric laminated composite beams:theoretical and experimental results[J]. Composite Science and Technology, 1984, 18(2): 104-121. |
| [15] |
YANG Jinshui, XIONG Jian, MA Li, et al. Vibration and damping characteristics of hybrid carbon fiber composite pyramidal truss sandwich panels with viscoelastic layers[J]. Composite Structures, 2013, 106: 570-580. DOI:10.1016/j.compstruct.2013.07.015 |
| [16] |
熊波, 林国昌, 张印桐, 等. 一种复合材料桁架的制备及弯曲承载性能分析[J]. 哈尔滨工业大学学报, 2014, 46(5): 46-50. |
 2016, Vol. 48
2016, Vol. 48