2. 北京工业大学 机械工程与应用电子技术学院, 100022 北京;
3. 哈尔滨工业大学 航天学院, 150001 哈尔滨
2. College of Mechanical Engineering and Applied Electronics Technology, Beijing University of Technology, 100022 Beijing, China;
3. School of Astronautics, Harbin Institute of Technology, 150001 Harbin, China
随着我国探月计划的推进,月球返回技术已由“嫦娥5”实验探测器成功验证,该技术对未来建立月球基地、开发月球资源至关重要[1-2].然而,传统的月球采样返回方式需要将探测器送入月球双曲轨道脱离月球引力场进而返回地球,燃料消耗极大(约810 m/s的速度脉冲)[3],因此如何利用尽量少的燃料将更多的月球资源返回地球,决定了未来开发月球的效益[4].
研究低能量返回轨道,主要关注两方面:1)月球探测器脱离月球影响球的最低能量需求; 2)如何在低能量脱离月球影响球的同时能够返回地球.对于前者,研究表明,100 km环月圆轨道上的探测器能够借助日月引力与地月椭圆运动的作用,以最低603 m/s左右的速度脉冲经地月平动点脱离月球影响球[5].对于后者,文献[6]在其研究中曾以仿真算例的形式证明了探测器能够从地月L2平动点逃逸后,经日地月引力共同作用返回地球.然而,月地低能返回轨道存在较强的引力混沌现象,飞行器微量的飞行状态偏差会导致终端状态明显的改变,甚至无法实现返回,利用传统的梯度法迭代设计轨道,或不能求取迭代所需的梯度数值,或使算法收敛迭代步长很难选取,导致迭代无法进行,因此,需要采用收敛性较强的轨道设计方法,保证轨道设计的成功率和计算效率.
事实上,月地低能返回轨道与Hiten号飞行器所使用的低能奔月轨道具有明显的对称性,其轨道设计方法也可对本文的研究提供参考[7].当前,主要有主矢量法、Halo轨道演化法、流形拼接法、智能搜索算法等寻优算法可代替传统打靶迭代法用于设计低能奔月轨道[8-12].其中,主矢量法利用极大值原理求取从地球出发到月球弹道式捕获所需的最小脉冲能量,但需要猜测本无物理意义的协状态初值,计算效率和自动化水平不高.Halo轨道演化法和流形拼接法利用了低能转移轨道所在的空间不变流形与平动点稳定/非稳定流形接近甚至相切的特性,快速获得低能转移轨道的初值,但是需要先花费大量时间计算空间不变流形管路,且对捕获后的轨道参数并没有加以限制.月地返回轨道要求探测器以严格的再入轨迹进入大气层,加之轨道本身的弱稳定性,上述这些轨道设计算法都很难获得符合工程任务的计算结果[9-12].而遗传算法在求取强非线性、多局部最优点的问题时具有较强的优势,适合本文中对月地低能返回轨道的设计工作[13-15].但其计算量大,求解精度与种群数量相关,因此需要对其进行改进.
本文针对月球非载人探测器返回轨道的设计问题,在椭圆四体问题下研究探测器的动力学特性,并提出了一种改进的混合自适应遗传算法,用于搜索最低返回能量,最终仿真结果表明,月球探测器可以月球椭圆轨道初始速度出发,经过地月L2平动点返回地球.
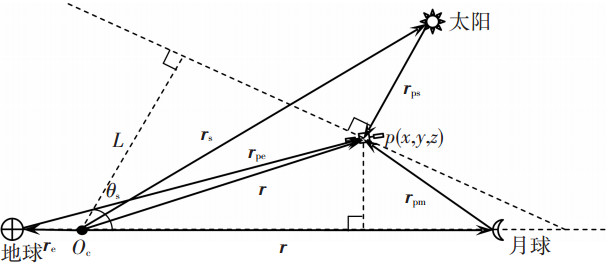
1 日地月多体动力学与低能返回轨道分析 1.1 探测器动力学模型研究月球低能返回轨道的设计问题,至少需要同时考虑日地月引力和月球椭圆运动对探测器的影响,因此,探测器动力学模型使用日地月星椭圆四体问题进行建模.模型建立在地月旋转坐标系中,以地月质心为原点,月心方向为x轴,月球轨道角动量方向为z轴,y轴与另外两轴形成右手系,如图 1所示.
|
图 1 月球低能返回轨道模型 |
探测器在地月旋转坐标系中的动力学方程矢量形式如下
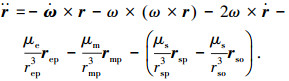
|
式中:μe、μm、μs分别为地球、月球和太阳的引力常数; rep、rmp、rsp分别为探测器相对于地球、月球和太阳的位置矢量; rso为太阳相对地月质心的位置矢量; ω为地月旋转角速度.
1.2 返回轨道特性分析设计月地低能返回轨道,首先需要研究确定返回轨道的存在性以及动力学特征.本文中,主要着眼于弹道式低能量返回轨道的设计问题,所以仅考虑月球探测器以单次脉冲变轨进入返回轨道返回地球.首先,为了验证返回轨道的存在性,利用数值搜索的方法,以月球白道100 km圆轨道为初始轨道,时间区间为2020年1月,以不同的月心经度为初始位置施加切向脉冲,使探测器进入一条半长轴为25 000 km的月球大椭圆轨道,在多体系统的作用下,可得到不同的发射时间和月心经度对应的轨道近地点半径分布图,如图 2所示.

|
图 2 探测器近地点分布情况 |
从分布图中可以看出,在一个月球运动周期内(约为28 d),不同的发射相位对应的轨道近地点高度分布可分为4个区域,而只有处于D区域时,探测器才有可能以单次变轨的形式低能量弹道式返回地球.图 3为地心惯性系下月球探测器低能量返回轨道,值得指出的是,图 2所示的轨道分布规律具有普遍性,几乎每个月均有1个低能量返回轨道发射窗口.

|
图 3 月球低能返回轨道(惯性系) |
通过仿真计算可知,选择合适的探测器发射状态,可实现低能量返回,然而此结论并不具有工程实践性,由于返回地球需要保证较高的再入点精度,因此需要对探测器返回轨道的终端再入点进行约束,并以此约束修正发射点参数,得到满足再入参数需求的低能返回轨道.
2 月球返回约束条件分析月球返回任务中,若不考虑探测器从月面起飞进入环月过渡轨道的发射段,可以假设探测器已经处于一条圆形环月轨道上,其高度为100 km,探测器从该轨道出发,转移至地球大气层边缘,考虑探测器在我国内蒙地区再入着陆,其轨道约束条件见表 1.
| 表 1 混合遗传算法计算结果 |
可见,对于工程可实现的月地低能返回轨道来说,是一个典型的多目标优化问题,通常,遗传算法对于这种强非线性优化问题具有较好的搜索性能,但是这种方法计算量较大,特别是对于月球低能返回轨道设计问题,需要同时优化点火时间、脉冲方向、脉冲大小等,计算量将呈指数增加,并且遗传算法的局部搜索能力不如梯度法,因此,若能设计兼顾全局寻优和局部快速收敛的混合算法,可以显著提高返回轨道设计的效率.
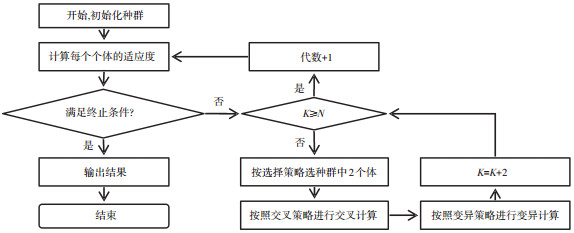
3 基于自适应交叉变异概率与牛顿迭代的混合自适应遗传算法 3.1 遗传算法的计算步骤遗传算法自上世纪70年代发展至今,已按照编码形式、进化法则等不同计算机制发展成多种子算法,广泛应用于信息、计算和应用科学等领域,但是其基本原理与流程仍然是通过模拟自然选择和自然遗传机制进行随机搜索,其计算流程如图 4所示[16-17].
|
图 4 遗传算法计算流程 |
使用遗传算法进行月地低能返回轨道的设计过程中,可以进行优化的控制变量有变轨时间、初始环月轨道倾角、变轨时刻探测器月心经度、变轨脉冲大小,采用混合编码形式为
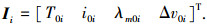
|
适应度函数值可以使用终端参数偏差的加权和,由于不要求控制变量与优化指标同维数,本文可以增加一些优化指标,如初始脉冲大小,以期能够求取既满足终端约束条件又最为节省发射能量的返回策略,因此适应度函数可以写为
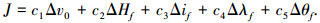
|
式中,加权系数c1~c5的选择影响着优化算法对某一设计指标的搜索敏感程度.本文中,利用加权系数对各个参数进行归一化处理,使得不同优化指标的变化范围趋于统一,有利于搜索的进行.具体的系数定义为:c1=1.73(km/s)-1; c2=6 378(km)-1; c3=c4=c5=180 (°)-1,此处需要指出的是,由于各设计指标均具有不同的量纲,为对其进行加权和计算,加权系数应对其进行量纲一的处理,因此系数的量纲为指标量纲的倒数.
3.3 算法流程针对上述优化问题的特点以及遗传算法与微分修正法的优缺点,提出了混合自适应遗传算法,算法的流程如下:
1) 随机产生初始群体作为父代并计算其适应度;
2) 对其中的个体以概率Pc进行编码-交叉-解码运算,产生子代并加入群体;
3) 对群体中的个体以概率Pm进行编码-变异-解码运算,产生子代并加入群体;
4) 对群体中的个体以概率Ps对指标J进行微分修正,产生的新个体替换原有个体;
5) 按照优胜劣汰的规则,淘汰弱势个体,保持种群规模.
3.4 自适应交叉与变异概率本文中,为了避免遗传算法概率性达到局部最优的情况,采用自适应交叉、变异和搜索概率进行补偿,以期避免陷入局部最优的情况发生,其中心思想是,对于群体较为集中的情况,增大种群的交叉与变异概率,增加逃离局部最优点的机会,同时,对于种群中较为优势的个体,增加搜索概率,使得算法收敛速度加快.实际计算中,以种群的最低适应度Fitmin、最高适应度Fitmax和平均适应度Fitave三者决定交叉、变异和搜索概率的大小,具体算法为:

|
式中:Pcmax、Pmmax、Psmax分别为个体最大交叉、变异与搜索概率.需要指出的是,搜索概率对不同个体是不同的,个体越占有优势,就有更大的几率进行进一步的搜索以快速到达最优点.
4 仿真分析 4.1 算法参数设置利用本文提出的混合自适应遗传算法进行月地低能返回轨道设计,需要对程序算法进行参数设置.本文中,选取探测器初始轨道高度为100 km,入射脉冲沿轨道切线方向施加,入射时刻范围为2020年1月1日至30日,入射时刻探测器月心经度为-180°~0°,变轨脉冲大小为600~650 m/s,环月轨道倾角为0°~90°,优化指标按照遗传算法的计算步骤进行定义,通过多次计算经验得到较好的个体最大交叉、变异与搜索概率为Pcmax=0.80%,Pmmax=0.05%,Psmax=0.05%,种群规模为2 000个,最大代数限制为100代.按照此设置进行搜索计算,可以较为迅速地搜索到所需的最优返回轨道.
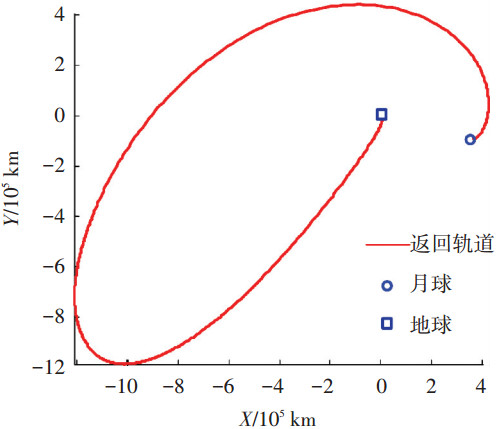
4.2 轨道设计结果利用上述混合自适应遗传算法对月球探测器低能量返回轨道设计问题进行求解,代入仿真程序计算,最终得到了最优的月球探测器低能量返回轨道(见图 5),返回参数见表 2.
|
图 5 低能返回轨道设计结果 |
| 表 2 混合遗传算法计算结果 |
与传统的双曲拼接方式相比,最低能量转移轨道所需的速度脉冲仅为其3/4,对于未来的资源运输任务来说,本阶段的燃料节约意味着可以减少地球向月球运送燃料的总量,而且能够提高资源运输量,对商业开发月球来说无疑显著提高了经济效益.
4.3 算法性能比较分析利用本文提出的混合自适应遗传算法进行月地低能返回轨道寻优计算,所使用的计算机系统性能配置为:计算机采用3.0 GHz单核处理器,4 G内存,计算程序使用Matlab8.0编程,整个仿真计算过程耗时约10 min,经31代计算后得到轨道设计结果.
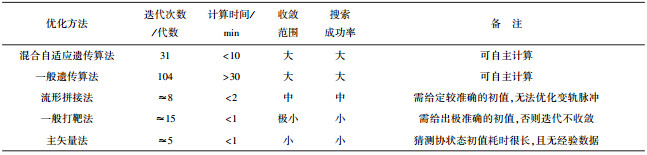
除本算例外,在研究过程中还使用相同算例对一般遗传算法、流形拼接法、一般打靶法等算法一并进行仿真计算以作比较,各算法的计算性能见表 3.
| 表 3 算法性能比较 |
需要指出的是,表 3中,流形拼接法、一般打靶法和主矢量法均可在短时间内迭代得到所需的月地低能转移轨道,且计算时间远优于遗传算法,但这种高效计算的前提是需要通过大量手动试凑得到较为准确的迭代初值,往往耗时远多于遗传算法且不能保证计算成功率.然而,这也表明,若能在初值猜测方面寻找突破口,实现快速、自主地给出迭代初值,将显著提高低能返回轨道的计算效率,得到比混合自适应遗传算法更优的轨道设计方法.
5 结论1) 在椭圆四体问题下建立探测器动力学模型,分析了低能返回轨道的存在性与规律性;设计一种结合迭代法的混合式自适应遗传算法,求解使得探测器以最低发射能量返回地球的发射时机、发射相位以及对应的速度脉冲.
2) 仿真结果表明,采用混合自适应遗传算法设计轨道,可利用相对较少的计算量得到优化的轨道参数,并实现完全自动化计算,无需人工给定迭代初值,具有较好的计算效率.
| [1] |
CARPENTERJ D, FISACKERLY R, De ROSA D, et al. Scientific preparations for lunar exploration with the European Lunar Lander[J]. Planetary and Space Science, 2012, 74(1): 208-223. DOI:10.1016/j.pss.2012.07.024 |
| [2] |
刘晖. 热烈庆祝"嫦娥五号"飞行试验器飞行任务取得圆满成功[J]. 航天返回与遥感, 2014(6): 2. |
| [3] |
COOPERSMITH J. The cost of reaching orbit:ground-based launch systems[J]. Space Policy, 2011, 27(2): 77-80. DOI:10.1016/j.spacepol.2011.03.001 |
| [4] |
CRAWFORD I A, ANAND M, COCKELL C S, et al. Back to the Moon:the scientific rationale for resuming lunar surface exploration[J]. Planetary and Space Science, 2012, 74(1): 3-14. DOI:10.1016/j.pss.2012.06.002 |
| [5] |
荆武兴, 刘玥. 椭圆三体问题下月球L2低能逃逸轨道设计[J]. 航空学报, 2014, 35(6): 1496-1504. |
| [6] |
IVASHKIN V V. Low energy trajectories for the Moon-to-Earth space flight[J]. Journal of Earth System Science, 2005, 114(6): 613-618. DOI:10.1007/BF02715945 |
| [7] |
KOONW S, LO M W, MARSDEN J E, et al. Low energy transfer to the Moon[J]. Celestial Mechanics and Dynamical Astronomy, 2001, 81(1/2): 63-73. DOI:10.1023/A:1013359120468 |
| [8] |
GRIESEMER P R, OCAMPO C, COOLEY D S. Optimal ballistically captured Earth-Moon transfers[J]. Acta Astronautica, 2012, 76: 1-12. DOI:10.1016/j.actaastro.2012.01.001 |
| [9] |
李雪华, 和兴锁, 宋明, 等. 基于不变流形的一种节能轨道设计[J]. 西北工业大学学报, 2011, 29(3): 390-393. |
| [10] |
徐明. 地月低能转移的发生条件及轨迹构造[J]. 力学学报, 2010, 42(2): 275-289. |
| [11] |
GONG Shengping, LI Junfeng, BAOYIN Hexi, et al. Lunar landing trajectory design based on invariant manifold[J]. Applied Mathematics and Mechanics, 2007, 28(2): 201-207. DOI:10.1007/s10483-007-0208-1 |
| [12] |
PONTANI M, TEOFILATTO P. Low-energy Earth-Moon transfers involving manifolds through isomorphic mapping[J]. Acta Astronautica, 2013, 91(10): 96-106. |
| [13] |
曾喻江. 基于遗传算法的卫星星座设计[D]. 武汉: 华中科技大学, 2007: 29-45.
|
| [14] |
BAYLEY D J, HARTFIELD R J, BURKHALTER J E, et al. Design optimization of a space launch vehicle using a genetic algorithm[J]. Journal of Spacecraft and Rockets, 2008, 45(4): 733-740. DOI:10.2514/1.35318 |
| [15] |
ABDELKHALIK O, GAD A. Hidden genes genetic algorithm for multi-gravity-assist trajectories optimization[J]. Journal of Spacecraft and Rockets, 2011, 48(4): 629-641. DOI:10.2514/1.52642 |
| [16] |
乔栋. 深空探测转移轨道设计方法研究及在小天体探测中的应用[D]. 哈尔滨: 哈尔滨工业大学, 2007: 92-93.
|
| [17] |
王亚敏, 乔栋, 崔平远. 从月球逃逸探测小行星的发射机会搜索[J]. 宇航学报, 2012, 33(12): 1845-1851. DOI:10.3873/j.issn.1000-1328.2012.12.020 |
 2016, Vol. 48
2016, Vol. 48