2. 江苏省物联网与控制技术重点实验室(南京航空航天大学), 210016 南京
2. Jiangsu Key Laboratory of Internet of Things and Control Technologies(Nanjing University of Aeronautics and Astronautics), 210016 Nanjing, China
借助于推力矢量技术和先进的气动布局,现代战机普遍具备大迎角下机动的能力.然而,当飞机大迎角机动时,由于气流分离使得气动力呈现高度非线性,尤其会呈现出非定常迟滞特性,飞行运动将产生明显的气动超调量和气动力时间滞后响应[1].如何消除大迎角机动中的非定常气动的影响,具有重要的实际意义.
国内外学者[2-3]针对非定常现象的建模进行了深入的研究,然而对于非定常气动对大迎角机动中飞行动力学的影响以及机动过程中控制器如何抑制和消除此类影响还需进一步考虑.文献[4]针对非定常气动对于飞行动力学的影响进行了分析.文献[5]在飞控系统设计时考虑了非定常气动力的抑制问题.为有效抑制机动飞行条件下的非定常气动影响,本文提出利用干扰观测器的方法来对非定常气动干扰进行观测和补偿,并进行了机动控制器设计.干扰观测器方法具有设计灵活、能充分利用干扰的已知信息等优点,且有较为成熟的理论和应用[6-7].为了结合干扰观测器进行机动控制器的设计,本文将飞机模型和非定常气动模型统一描述成以期望迎角为参数的LPV形式.LPV模型在飞行器控制中有较多应用[8].相比于其他方法,本文中采用此类模型能够有效描述飞机大迎角时的非线性特性,同时又具有线性系统的形式[9],便于控制器设计.
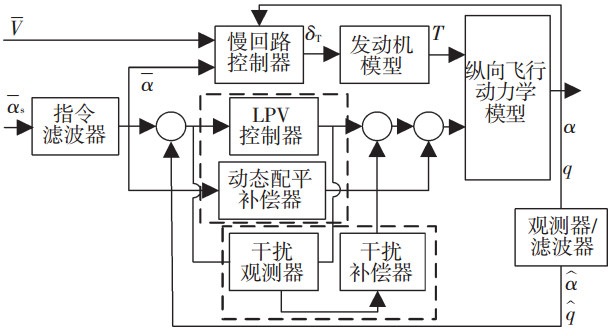
1 机动控制结构飞机的纵向大迎角机动属于短周期运动,控制的目的在于对姿态量进行有效控制,而对于飞行速度只需要保持在一定水平.本文所设计的机动控制器结构如图 1所示,整个控制器分为快回路和慢回路两个部分,在慢回路中依靠推力控制使得飞机机动过程中保持一定速度,而快回路中指令的跟踪控制是设计工作的重点,需要满足以下要求:1)对迎角指令进行有效跟踪;2)对非定常气动干扰进行有效抑制.图 1中V为飞行速度,α为迎角,q为俯仰角速度,δT为发动机油门,T为发动机推力.
|
图 1 控制结构示意 |
飞机机动过程中,控制系统的性能需要满足文献[10]中规定的飞行品质要求.对于纵向短周期机动,驾驶杆输入指令与飞机响应值之间的等效系统模型为

|
(1) |
式中:ylong为纵向机动控制量;δstick为驾驶杆输入;ζsp、ωsp分别为等效阻尼比和自然频率,满足ωsp≈0.03Veq, 0.35≤ζsp≤1.3;Veq为等效空速.
控制系统通过在驾驶杆输入端添加前置指令滤波器,可以生成满足飞行品质要求的参考指令.大迎角机动中纵向通道的驾驶杆输入为期望迎角指令αs,经指令滤波器后,输出参考迎角指令α进入内环控制系统.
1.2 慢回路控制器慢回路控制器的作用是在进行飞机姿态调整时保持恒定飞行速度,同时兼顾航迹控制.大迎角机动过程中舵面偏转信号用来控制飞机姿态,因而飞行速度则主要依靠调节发动机推力调节.这里采用文献[11]中的飞行/推进耦合器方案来进行速度回路的控制,控制律中引入迎角反馈以减小迎角改变引起的速度变化,具体控制律为
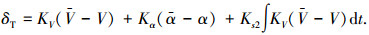
|
式中:δT为发动机油门;V、V分别为期望速度和实际速度;α、α分别为期望迎角和实际迎角;KV、Kα、Ks2分别为速度、迎角以及积分系数.
1.3 快回路控制器快回路控制器由LPV控制器和动态配平补偿器组成.飞机在大迎角机动中通常处于动态配平状态,因此传统的围绕静态平衡点进行线性化获得的单一线性模型不能很好地近似大迎角机动过程中的飞行动力学.由于迎角变化范围较大,此时飞行运动方程的非线性特性必须加以考虑.
动态配平补偿器的作用是根据期望迎角指令求解动态配平点,并将解得的配平输入值引入控制端进行偏置补偿,从而将期望指令的跟踪问题转化为误差系统的镇定问题.通过状态变换方法[12],将纵向快回路非线性动力学方程近似成以下LPV形式:
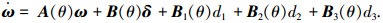
|
(2) |
式中:ω∈R2为快回路误差状态; δ∈R2为误差输入; θ为调度参数; d1、d2分别为非定常升力和俯仰力矩干扰; d3为附加干扰; A(θ)、B(θ)、B1(θ)、B2(θ)分别为随参数θ变化的相应维数的矩阵.
首先对不包含干扰的标称LPV误差系统进行镇定控制器设计,使之具有良好的动态性能和鲁棒特性.同时,在控制器设计时通过施加幅值约束来保证多个控制输入能够较好地进行分配.考虑到迎角等信号在实际测量中存在误差,采用观测器或滤波器对快回路状态量进行估计.
1.4 非定常干扰观测器非定常干扰观测器的作用是对非定常气动干扰进行观测和补偿,包括基于LPV模型的干扰观测器和干扰补偿器.依据动力学建模的思想,可将非定常气动迟滞现象用一阶微分方程的形式来表示.将系统(2)中的非定常气动干扰和附加干扰综合成外部干扰d,其模型可由以下LPV系统表示:

|
(3) |
式中:d=(d1, d2, d3)T; N=I; M(θ)为参数依赖的相应维数的矩阵; θ为与飞机LPV模型相同的调度参数.
基于建立的外部LPV干扰模型,设计干扰观测器对系统(2)中的干扰信号进行观测,并在控制端进行补偿.非定常俯仰力矩干扰对于机动过程有较大影响,由于其处于力矩通道内,可使用控制力矩全部抵消;而非定常升力处于升力通道内,对于采用鸭式布局的推力矢量飞机来说,利用前、后舵面偏转所产生的直接力不能完全提供补偿,然而由于其对于机动过程影响较小,因此这里采用部分补偿的方式来对机动过程进行适当修正.
2 LPV模型的建立飞机在大迎角机动过程中的动态特性随着动态平衡点的迁移而变化.在动态配平中,将速度和推力等慢变量当作已知量,则动态平衡点由迎角信号唯一确定,可将快回路动力学方程转化成以迎角信号为调度参数的LPV系统.同时机动过程中的非定常气动力也可表示成以迎角信号为调度参数的LPV系统,将控制对象统一成同一种形式有利于控制器的设计.
2.1 飞机的LPV模型考虑纵向快回路非线性飞行动力学方程:
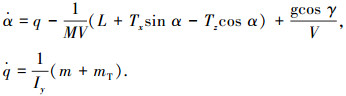
|
(4) |
式中:α为迎角;q为俯仰角速度;V为飞行速度;γ为航迹倾斜角;M为飞机质量;Iy为绕y轴的转动惯量;g为重力加速度;Tx、Tz分别为x轴和z轴方向的推力;L为总升力;m、mT分别为总气动俯仰力矩和由推力矢量产生的俯仰力矩.在考虑非定常的情况下,总气动力和力矩表示为定常项与非定常项之和,即
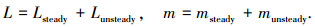
|
这里首先在定常情况下建立标称误差系统的LPV模型.假定速度V和航迹倾斜角γ为已知量,并将飞机的迎角信号α分解为快变部分和慢变部分,即
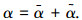
|
(5) |
式中:慢变部分α为飞机的期望迎角,作为系统的调度变量;而快变部分
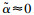
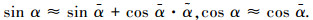
|
(6) |
对于定常升力和俯仰力矩,采用线性叠加气动导数模型,并使用冻结系数法,可得:
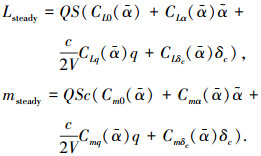
|
(7) |
式中:CL0、CLα、CLq、CLδc分别为零升力系数、迎角升力导数、俯仰角速度升力导数、鸭翼升力导数;Cm0、Cmα、Cmq、Cmδc分别为零升俯仰力矩系数、俯仰静稳定性导数、俯仰阻尼导数、俯仰操纵导数;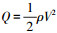
飞机推力矢量产生的力和力矩可表示为:

|
(8) |
式中:T为发动机推力;δz为推力矢量偏转角;xT为推力矢量喷嘴到飞机质心之间的距离.
将式(6)~(8)代入到式(4)中,可以将非线性动力学方程化为以下形式:
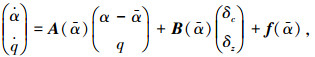
|
(9) |
其中
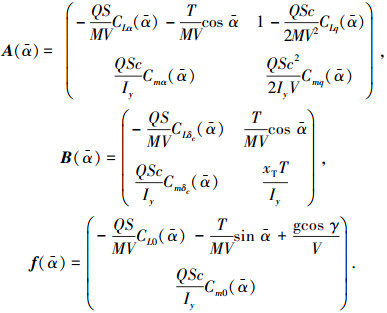
|
现设计动态配平补偿器,根据动态配平以及舵面分配条件,同时令式(9)左边为零,可得:
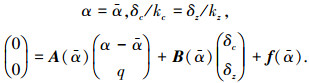
|
(10) |
式中:kc、kz分别为舵面分配系数.式(10)为包含未知量α, q, δc, δz的线性方程组,当α给定后,可通过求解得到动态平衡点的配平输入值和状态值:
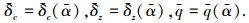
|
(11) |
一方面动态配平补偿器按照式(11)进行设计,另一方面,由于q(α)为α的可导函数,对其求时间t的导数可得
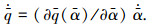
|
(12) |
通过令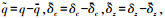

|
(13) |
将式(12)代入系统(13),可得到纵向快回路系统的LPV形式为
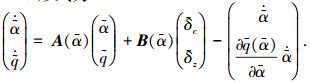
|
(14) |
注 式(14)表示的LPV模型中最后一项为参数动态项,这样处理的目的是为了更精确地描述原方程的非线性特性,使得模型更为可靠.文献[13]中也考虑了这一动态项,并采用状态变换法将其变换为与内部状态有关的准LPV项,而在本文中通过式(5)的处理,可将非线性模型转化为以快变误差信号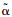
在控制器设计时,将参数动态项当作附加干扰处理,即令
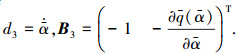
|
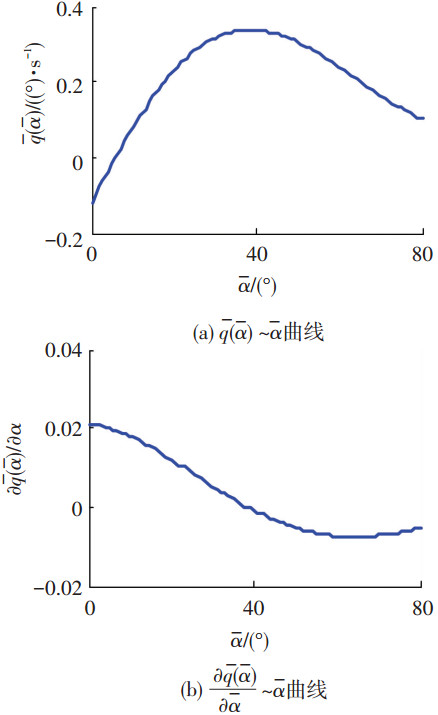
图 2给出了一组典型条件下的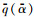
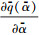
|
图 2
给定条件下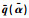  |
系统(2)中的外部干扰包括非定常气动干扰和附加干扰,需要分别进行建模,并统一表示成式(3)所示的复合干扰模型.非定常气迟滞现象是由于流场条件变化而产生的,因而非定常气动力表现为时间的函数.在对其进行建模时,通用的方法是采用一阶线性或非线性微分方程的形式进行表征.文献[14]在进行纵向非定常气动力建模研究时,将其表示为以下形式的参数依赖的一阶微分方程:
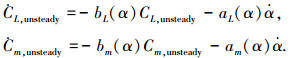
|
(15) |
式中:CL, unsteady、Cm, unsteady分别为非定常气动力和力矩系数;bL(α)、aL(α)、bm(α)、am(α)分别为依赖于迎角的模型参数.文献[15]给出了一组非定常升力和俯仰力矩模型参数,如图 3所示.

|
图 3 非定常俯仰力矩模型参数[15] |
模型(15)具有参数为迎角信号α的LPV系统的形式,为了与建立的飞机模型(14)具有统一的调度参数,将模型中实际迎角信号α用期望迎角α替换,并分别将非定常升力和俯仰力矩系数记为d1和d2,则对式(2)有

|
进一步建立附加干扰d3的模型,根据指令滤波器(1)可以将d3的模型近似为
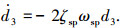
|
将非定常干扰模型和附加干扰模型联立,可表示成式(3)中的LPV模型形式,其中参数为
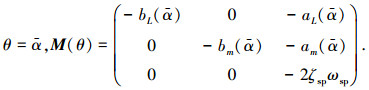
|
经过以上处理,干扰模型和飞机模型具有统一调度参数,便于在统一框架下设计控制器和干扰观测器.由于LPV模型具有微分包含的结构,对模型的精确性依赖较小,因此基于LPV模型设计干扰观测器相比直接基于非线性系统具有较强的鲁棒性.
3 基于LPV系统的设计方法干扰观测器方法具有高增益观测器分离原理的优点,即允许把设计过程分解为两个步骤,首先设计一个状态反馈控制器,以稳定标称系统并满足性能设计要求,再使用干扰观测器对系统中的干扰进行观测,并在控制端加以补偿.由于系统模型和干扰模型都是LPV形式,因此在设计中将相应定理扩展至LPV系统.
首先,针对以下标称LPV系统为

|
(16) |
设计状态反馈控制器δ1=Kω.假设参数θ属于紧集Ω,给定σK>0,如果对于所有θ∈Ω,存在对称正定矩阵Q和矩阵Y,使得

|
(17) |
则控制矩阵可设计为K=YQ-1,使得闭环系统是渐进稳定,设计参数σK的作用是保证系统有较快的收敛特性.另外,为使得控制舵面偏转较小,应用以下输入有界条件:
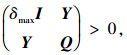
|
式中δmax为最大舵面偏转值.同时考虑到迎角信号在测量中存在误差,在控制器实施时采用其估计值代替测量值,即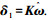
其次,针对由外部系统(3)产生的干扰信号,可设计以下形式的干扰观测器:
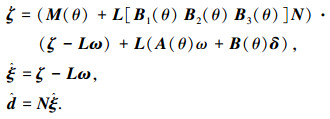
|
(18) |
当给定σL>0,如果对于所有θ∈Ω,存在对称正定矩阵P和矩阵X,使得
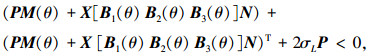
|
(19) |
则观测器增益L可设计为L=P-1X.为了保证观测器尽快收敛,需要设计较大衰减率σL.
注 对式(17)和式(19)的求解可采用网格法[16]或凸包法[17],将无穷个不等式转化为有限个.
若所观测干扰和系统输入满足匹配条件,可直接在输入端进行补偿.在实际工程中,为了保证系统的输入在合理范围内,干扰信号需要乘以适当的系数矩阵F:
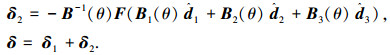
|
(20) |
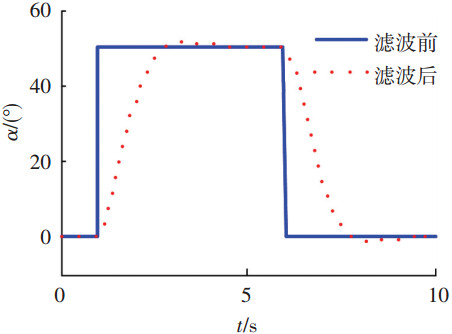
将所设计的控制器方案应用于非定常气动条件下,飞机的大迎角俯仰机动过程,并通过仿真对控制效果进行验证.仿真中飞机的模型选用X-31,具备推力矢量装置和鸭式布局,采用文献[15]中给出的模型来反映非定常迟滞现象.飞机的指令为图 4中实线所示的方波信号,命令飞机作迎角50°快速上仰和下俯机动.指令滤波器设计参数选择为:ωsp=2, ζsp=0.75,图 4中虚线为经滤波后的指令信号.
|
图 4 大迎角机动指令 |
首先进行标称控制器的设计,将飞机模型化简为式(3)中的LPV形式,并采用式(17)进行控制矩阵K的计算.在进行线性矩阵不等式计算时采用网格法,将0°~80°的迎角空间按5°间隔取17个节点进行计算,即同时满足17个线性矩阵不等式.设计参数σK和计算结果如下:

|
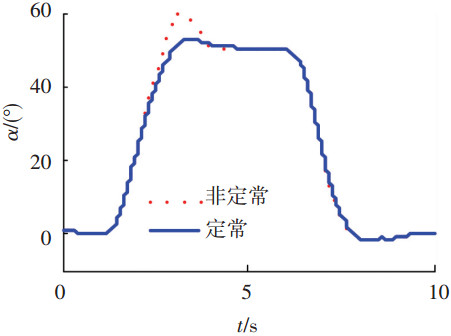
标称控制器作用下的系统响应曲线如图 5所示,从图 5中可以看出,在不存在非定常气动影响的情况下,标称控制器能够较好地控制飞机完成上仰和下俯机动;当存在非定常气动力时,飞机的上仰机动过程出现振荡和超调,但是非定常气动力对飞机下俯过程的影响则不明显.因此,采用干扰观测器对非定常气动干扰进行观测和补偿是十分必要的.
|
图 5 标称控制器迎角响应 |
进一步进行干扰观测器和补偿器设计,针对近似的外部干扰模型(3),设计如式(18)所示的干扰观测器,并采用式(19)获得观测器增益L,在计算过程中选取与上述相同的节点,设计参数σL和计算结果如下:
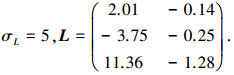
|
当观测出非定常干扰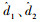
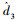
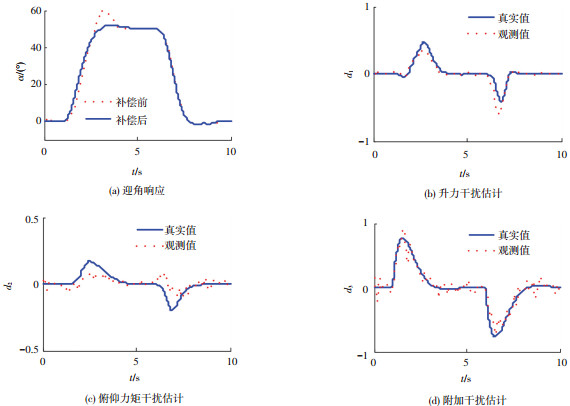
|
图 6 干扰观测器方法迎角响应与干扰估计 |
为了进行对比,针对LPV系统(3)采用H∞方法进行非定常条件下飞行控制器的设计,仿真结果如图 7所示.从图 7中的迎角响应曲线可以看出,H∞控制器能够控制飞机完成机动,并且对非定常干扰进行有效抑制.当相比于干扰观测器方法,H∞控制器对于上仰机动的响应较慢,同时由于采用高增益反馈使得舵面容易产生饱和.
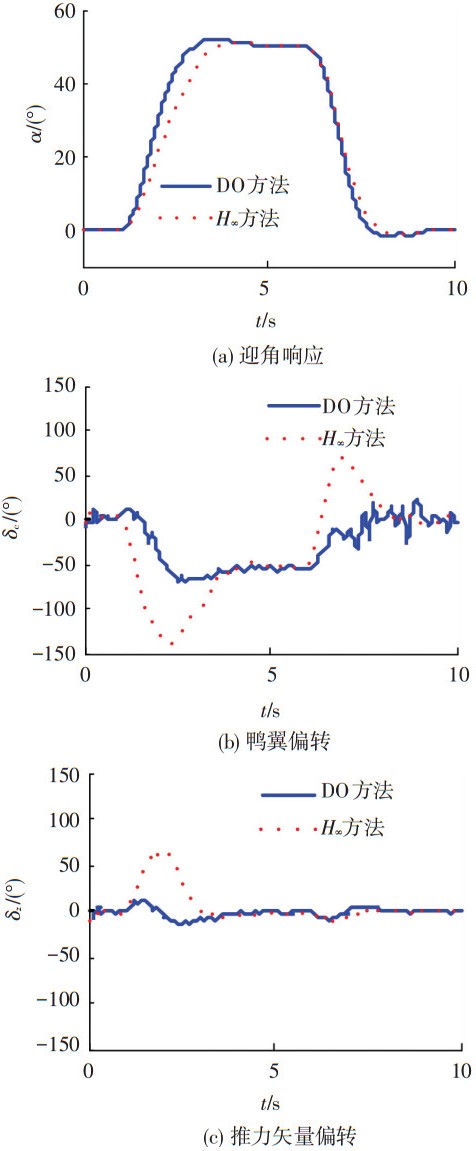
|
图 7 干扰观测器方法与H∞方法仿真结果对比 |
1) 通过设计干扰观测器,能够有效地对大迎角机动中非定常力矩干扰进行观测和补偿.由于干扰观测器具有分离特性,因此可对其独立设计,工程应用较为灵活.
2) 通过将飞机模型和干扰模型转化为LPV形式,便于统一设计标称控制器和干扰观测器.干扰观测器方法能够充分利用干扰的已知的模型信息,因而相比于H∞等干扰抑制方法,其具有控制代价小的优点.
| [1] |
龚正. 先进飞行器非定常气动力建模、控制律设计及验证方法研究[D]. 南京: 南京航空航天大学, 2011.
|
| [2] |
GOMAN M, KHRABROV A. State-space representation of aerodynamic characteristics of an aircraft at high angles of attack[J]. Journal of Aircraft, 1994, 31(5): 1109-1115. |
| [3] |
王峥华, 史志伟. 基于状态空间法的横航向非定常气动力建模[J]. 飞行力学, 2010, 28(6): 16-20. |
| [4] |
史志伟, 尹江辉, 明晓. 非定常自由来流对飞机过失速机动特性的影响[J]. 空气动力学学报, 2008, 26(4): 486-491. |
| [5] |
朱恩, 郭锁凤. 在动态逆飞控系统中处理非定常气动力的方法[J]. 南京航空航天大学学报, 1998, 30(5): 584-587. |
| [6] |
CHEN Mou, CHEN Wenhua. Disturbance-observer-based robust control for time delay uncertain systems[J]. International Journal of Control, Automation and Systems, 2010, 8(2): 445-453. |
| [7] |
孙兆伟, 邬树楠, 李晖. 带有干扰观测器的凝视航天器姿态变结构控制[J]. 哈尔滨工业大学学报, 2010, 42(9): 1374-1378, 1417. DOI:10.11918/j.issn.0367-6234.2010.09.006 |
| [8] |
马清亮, 郑建飞, 蔡宗平, 等. 空间飞行器大角度姿态机动混合H2/H∞控制[J]. 哈尔滨工业大学学报, 2012, 44(11): 105-111. DOI:10.11918/j.issn.0367-6234.2012.11.021 |
| [9] |
SCHERER C. Control of linear parameter varying systems with applications[M]. Berlin: Springer, 2012.
|
| [10] |
Military standard. Flying qualities of piloted vehicles: MIL-STD-1797A[S]. Washington, DC: Department of Defense, 1990.
|
| [11] |
申功璋, 高金源, 张津. 飞机综合控制与飞行管理[M]. 北京: 北京航空航天大学出版社, 2008.
|
| [12] |
TOTH R. Modeling and identification of linear parameter-varying systems[M]. Heidelberg: Springer, 2010.
|
| [13] |
PARAGEORGIOU G, GLOVER K, D'MELLO G, et al. Development of a "reliable" LPV model for the longitudinal dynamics of DERA's VAAC Harrier[C]//AIAA Guidance, Navigation, and Control Conference. Denver: AIAA, 2000: 4459.
|
| [14] |
MURPHY P C, KLEIN V, SZYBA N M. Progressive aerodynamic model identification from dynamic water tunnel test of the F-16XL aircraft[C]//AIAA Atmospheric Flight Mechanics Conference and Exhibit. Rhode Island: AIAA, 2004: 5277.
|
| [15] |
KLEIN V, MURPHY P C. Estimation of aircraft nonlinear unsteady parameters from wind tunnel data: NASA TM-1998-208969[R]. Hampton: NASA Langley Research Center, 1998.
|
| [16] |
RUGH W J, SHAMMA J S. Research on gain scheduling[J]. Automatic, 2000, 36(10): 1401-1425. DOI:10.1016/S0005-1098(00)00058-3 |
| [17] |
ANSTETT F, MILLERIOUX G, BLOCH G. Polytopic observer design for LPV systems based on minimal convex polytope finding[J]. Journal of Algorithms & Computational Technology, 2009, 3(1): 23-43. |
 2016, Vol. 48
2016, Vol. 48


