出于气动效率和隐身特性的考虑，飞翼布局无人机取消了平尾和垂尾等部件.由于平尾的缺失，飞翼布局无人机通常为纵向弱稳定且纵向阻尼非常小^[1].飞翼布局无人机在自动着陆过程中，飞行高度和空速都比较低，而且受到时变干扰影响，常规的PID控制方法难以精确控制无人机的空速、姿态和轨迹，需要采用鲁棒性强的控制方法来实现飞翼布局无人机的纵向着陆控制.

反步控制是一种常用的非线性控制方法^[2-4]，其设计过程是从系统最后一步基于Lyapunov稳定性理论逐步向前递推控制律，在这一过程中，需要对虚拟控制量进行求导，导致“微分爆炸”现象的产生.为此，Swaroop等^[5]提出“动态面控制”方法以解决“微分爆炸”的问题，然而，如果考虑动态面控制里低通滤波器的时间延迟，动态面控制容易导致系统振荡甚至发散^[6].文献[7]研究了吸气式高超声速飞行器纵向运动反步控制，引入了鲁棒微分器估计虚拟控制量的导数，解决了虚拟控制量求导运算复杂的问题.文献[8]针对不确定非仿射纯反馈非线性系统，采用反步自抗扰控制方法，分别利用跟踪微分器和扩展状态观测器估计虚拟控制量的导数和扰动部分，仿真结果验证了该方法的可行性.为保证飞翼布局无人机纵向着陆控制的性能，必须有效抑制干扰的影响.干扰观测器通过构建新的动态系统对干扰进行估计，在控制系统的设计中得到广泛应用^[9-10].文献[11]采用干扰观测器与终端滑模设计了高超声速飞行器的飞行控制系统，通过滑模干扰观测器估计和补偿复合干扰，提高了控制器的鲁棒性.文献[12]采用super twisting滑模干扰观测器结合反步控制成功的应用在飞机上，抑制了复合干扰的影响，取得了良好的效果.

在上述文献基础上，本文研究受扰飞翼布局无人机纵向着陆控制问题.针对反步控制中子系统存在的干扰，设计super twisting滑模干扰观测器对干扰进行估计与补偿，为解决反步控制虚拟控制量求导复杂这一问题，设计了跟踪微分器对虚拟控制量进行求导，为进一步增强控制系统的鲁棒性，增加L₂鲁棒项以抑制观测器干扰估计误差和跟踪微分器微分误差的影响，使得系统满足耗散不等式，仿真结果证明了控制器具有良好的鲁棒跟踪控制性能.

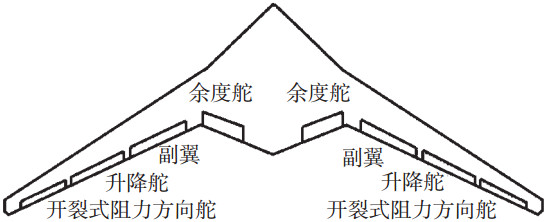
1 飞翼布局无人机纵向动力学模型

本文研究的大展弦比飞翼布局无人机如图 1所示，无人机的舵面配置为4组8个舵面，从内到外分别是余度舵、副翼、升降舵、开裂式阻力方向舵，其中余度舵为冗余舵面以提高无人机的操纵可靠性.开裂式阻力方向舵与常规的侧力方向舵不同，为新型的阻力类偏航舵面，其实现偏航操纵的原理是利用开裂式舵面上、下两片对称偏转所附加的阻力来产生偏航力矩，偏角范围为0°~90°.当左右两侧开裂式阻力方向舵偏转相同角度时，产生的偏航力矩相互抵消，而会产生较大的阻力.由于本文研究的是飞翼布局无人机纵向着陆控制，文中的开裂式阻力方向舵偏角δ_r即开裂式阻力方向舵左右两侧的偏角都为δ_r.

考虑系统参数不确定、未建模动态和外部时变干扰，忽略横侧向的影响，只考虑纵向运动，飞翼布局无人机纵向着陆动力学方程为如下包含不确定项的非线性系统：

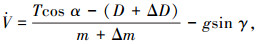
(1)

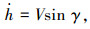
(2)

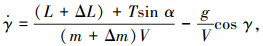
(3)

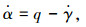
(4)

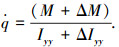
(5)

式中:V、h、γ、α、q分别为飞翼布局无人机的空速、高度、航迹倾斜角、迎角和俯仰角速率; m为无人机质量; Δm为无人机质量参数不确定性; I_yy为转动惯量; ΔI_yy为转动惯量参数不确定性; T为发动机推力; D、L、M分别为精确建模的阻力、升力和俯仰力矩; ΔD、ΔL、ΔM为无人机阻力、升力及俯仰力矩的建模误差及外部干扰.力和力矩具有如下的表达形式:

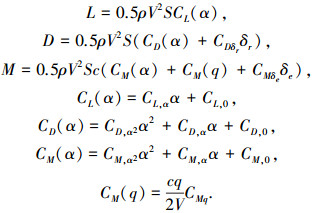
式中：ρ为空气密度; S为参考面积; c为平均气动弦长; C_L(α)、C_D(α)、C_M(α)+C_M(q)分别为无人机除舵面外精确建模的升力系数、阻力系数和俯仰力矩系数; C_Dδr为开裂式阻力方向舵阻力舵效; C_Mδe为升降舵俯仰舵效; C_Mq为纵向阻尼导数; δ_e为升降舵偏角; δ_r为阻力方向舵偏角.

2 空速控制器设计 2.1 阻力方向舵空速控制方案分析

将飞翼布局无人机纵向着陆控制问题分解为空速子系统和高度子系统.对于空速控制子系统，在纵向着陆过程直线下滑段，采用工程估算的方法，飞翼布局无人机的加速度满足

考虑单独采用发动机控制空速的情况, 此时阻力方向舵关闭，偏角为δ_r=0，迎角选取为4°，航迹倾斜角为-2.5°，当发动机推力从慢车状态(推力为最大推力的5%)到最大推力状态时，即发动机推力为0.05T_max~T_max时，无人机的加速度范围为0.167~4.190 m/s².可见，大展弦比飞翼布局无人机的全机升阻比很大，在下滑段，即使发动机工作在最小推力的慢车状态，无人机的空速仍然会增加，单独采用发动机无法实现无人机纵向着陆过程的空速控制.

开裂式阻力方向舵为飞翼布局无人机空速控制的有效补充，考虑采用阻力方向舵控制空速的情况，在直线下滑段，将发动机油门偏度设置为0.2，采用左右两侧开裂式阻力方向舵对称偏转相同角度δ_r增加阻力对空速进行控制，当δ_r的偏转角从0°增加到90°时，无人机加速度范围为0.803~-0.893 m/s²，可见，将发动机油门偏度固定为0.2，采用左右两侧开裂式阻力方向舵偏转相同角度δ_r增加阻力可实现对空速的控制.

2.2 L₂增益空速控制器设计

飞翼布局无人机纵向着陆控制模型空速子系统式(1)可写为

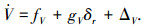
(6)

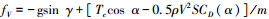
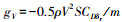
式中：; ; Δ_V为空速子系统的干扰.本文采用基于super twisting算法的滑模干扰观测器对速度子系统的干扰Δ_V进行估计与补偿，有如下定理.

定理1 对于空速控制模型式(6)，如果干扰Δ_V连续可微且一阶导数有界，即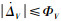，构造如下super twisting滑模干扰观测器：

(7)

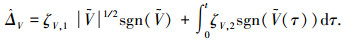
(8)

式中：为辅助滑模变量；为滑模干扰观测器对空速的估计值; 参数ζ_{V, 1}, ζ_{V, 2}满足，则式(8)的将在有限时间内实现对复合干扰Δ_V的估计.

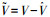
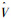
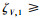
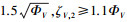
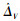
为证明定理1，首先给出如下引理.

引理1 对于受扰super twisting二阶滑模控制算法^[13-14]

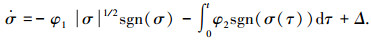
如果干扰Δ连续可微且一阶导数有界，即有，参数φ₁, φ₂满足则系统状态有限时间内收敛到

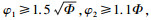
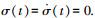
证明 将式(6)与式(7)相减，代入式(8)得

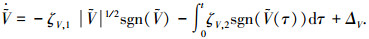
(9)

由引理1可知将会在有限时间收敛到0，由式(9)减去式(8)可得

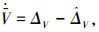
即在有限时间内，速度子系统的干扰Δ_V可由式(8)的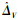估计.

定义空速跟踪误差e_V=V－V_c，对其求导可得

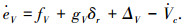
结合super twisting滑模干扰观测器与L₂增益理论，空速子回路控制律设计为

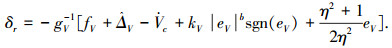
对于空速子系统，干扰信号选为观测器干扰估计误差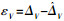，评价信号选取为e_V.

3 高度控制器设计 3.1 高度控制模型

高度子系统的设计以航迹倾斜角指令γ_c代替高度指令h_c作为高度子系统的跟踪信号.定义高度跟踪误差e_h=h－h_c，对其求导可得

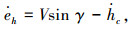
因此γ_c指令可设计为

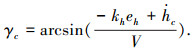
式中，k_h＞0为控制增益.在本文设计中，高度子系统均以如下的航迹倾斜角子系统代替：

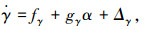
(10)

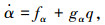
(11)

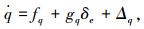
(12)

(13)

式中：Δ_γ、Δ_q分别为高度子系统航迹倾斜角通道与俯仰角速率通道的干扰.飞翼布局无人机纵向动力学模型式(1)~(5)，主要考虑的不确定因素为转动惯量不确定、无人机质量不确定、气动参数不确定、附加的时变干扰力矩等不确定因素，包含不确定因素的动力学模型式(3)、(5)减去控制模型式(10)、(12)中精确建模部分即可以得到干扰Δ_γ, Δ_q的表达式：

3.2 反步L₂增益高度控制器设计

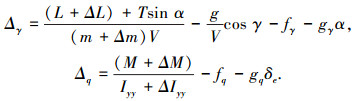
利用反步技术结合L₂增益方法对高度子系统的控制律进行设计.

步骤1 定义虚拟反馈误差如下：

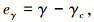
(14)

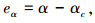
(15)

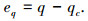
(16)

式中：α_c、q_c分别为待设计的虚拟控制量，对式(14)进行求导得

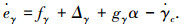
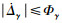
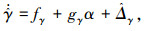
对于高度子系统航迹倾斜角通道式(10)，如果干扰Δ_γ连续可微且一阶导数有界，即，构造如下super twisting滑模干扰观测器:

(17)

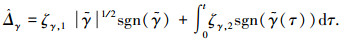
(18)

式中: 为辅助滑模变量; 为滑模干扰观测器对航迹倾斜角的估计值; ζ_{γ, 1}、ζ_{γ, 2}分别为干扰观测器参数且满足，则式(18)的将在有限时间内实现对干扰Δ_γ的估计，观测器的稳定性证明与定理1类似.

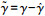
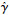
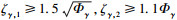
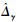
控制律用到指令γ_c的导数信息，由于存在噪声等原因，直接对其求导会产生高频噪声，本文采用跟踪微分器获得所需的导数信息，该微分器具有良好的噪声抑制性能，其形式如下：

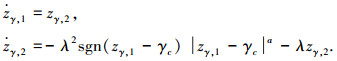
式中:z_{γ, 1}、z_{γ, 2}分别为微分器的状态变量; a、λ分别为设计参数，只要其满足不等式0<a<1, λ>0, 则z_{γ, 2}就能跟踪上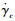，同时z_{γ, 1}跟踪上γ_c.

为进一步增加控制系统的鲁棒性，抑制干扰观测器估计误差和跟踪微分器微分误差的影响，结合L₂增益理论，增加鲁棒项使得系统满足耗散不等式，使干扰信号到性能输出的L₂增益不超过设定的正实数.设计虚拟控制律α_c为

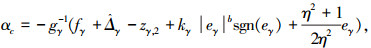
式中，将super twisting滑模干扰观测器的干扰估计误差与跟踪微分器的微分估计误差之和定义为系统干扰信号，即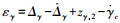，将虚拟反馈误差e_γ选取为系统评价信号.

步骤2 对虚拟误差式(15)进行求导得

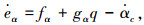
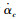
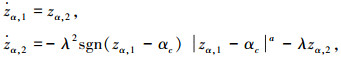
同理，由于对α_c直接求导会引入高频噪声，采用噪声抑制性能良好的跟踪微分器来估计为:

式中z_{α, 2}为α_c的微分估计值.虚拟控制律设计为

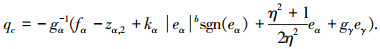
对于高度子系统迎角通道，干扰信号选取为迎角通道跟踪微分器的微分估计误差，即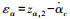，系统评价信号选取为e_α.

步骤3 对虚拟误差式(16)进行求导得

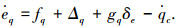
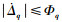
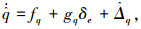
对于高度子系统俯仰角速率通道式(12)，如果干扰Δ_q连续可微且一阶导数有界，构造如下super twisting滑模干扰观测器:

(19)

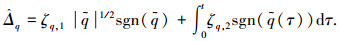
(20)

式中: 为辅助滑模变量; 为滑模干扰观测器对俯仰角速率的估计值; 参数ζ_{q, 1}, ζ_{q, 2}满足，则式(20)的将在有限时间内实现对复合干扰Δ_q的估计，观测器的稳定性证明与定理1类似.

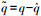
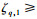
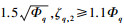
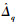
同理，由于对q_c直接求导会引入高频噪声，采用噪声抑制性能良好的跟踪微分器来估计: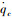

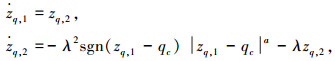
式中z_{q, 2}为q_c的微分估计值.控制律设计为

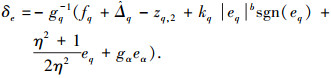
对于无人机高度子系统俯仰角速率通道，干扰信号选取为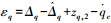，为俯仰角速率通道观测器的干扰估计误差与跟踪微分器的微分估计误差之和，系统评价信号选取为e_q.

4 稳定性分析

对于纵向着陆控制系统，设计Lyapunov函数为

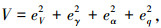
则Hamilton函数设计为

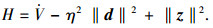
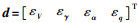
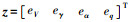
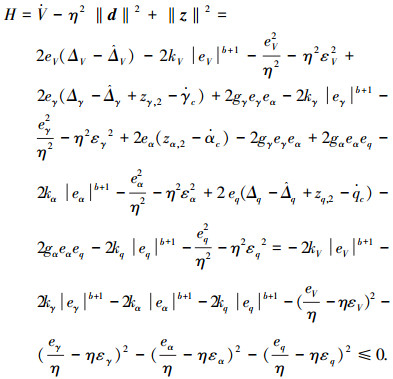
式中:干扰信号，系统评价信号选取为.

(21)

对式(21)两边同时进行积分, 可得

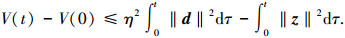
可知着陆控制系统满足耗散不等式，即从干扰d到性能输出z的L₂增益不超过η，由于d有界，纵向着陆控制系统是一致最终有界稳定的.

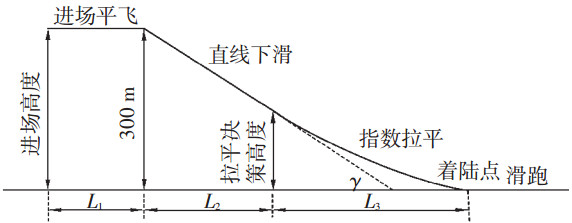
5 仿真与结果分析 5.1 仿真参数设定

无人机的纵向着陆过程分为进场平飞、直线下滑、末端拉平阶段，着陆过程如图 2所示.

本文的飞翼布局无人机着陆的空速指令为V_c=68 m/s，高度指令如下:

设在仿真零时刻开始，转动惯量施加-20%不确定，无人机质量施加+10%不确定，气动参数施加-30%的不确定，并同时加入时变干扰

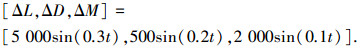
为了验证本文所提纵向着陆控制方案的有效性，现对以下两种控制方案进行仿真对比.

方案1 本文基于super twisting滑模干扰观测器和跟踪微分器的飞翼布局无人机反步L₂增益纵向着陆鲁棒控制方案.其中，super twisting滑模干扰观测器参数选取为：ζ_{γ, 1}=1，ζ_{γ, 2}=1，ζ_{q, 1}=1，ζ_{q, 2}=1，ζ_{V, 1}=1，ζ_{V, 2}=1.跟踪微分器参数选取为：a=0.5，λ=100.反步L₂增益控制器参数选取为：k_h=0.1，k_γ=0.5，k_α=1.5，k_q=4.5，k_V=1，b=0.5，η=2.

方案2 传统的PID纵向着陆控制方案.

1) 高度跟踪控制律为：

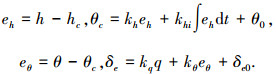
2) 采用开裂式方向舵的速度控制律为：

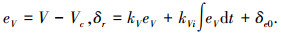
式中:控制器参数为k_h=－0.01，k_hi=－0.0001，k_q=2，k_θ=2，k_V=0.52，k_Vi=0.018.

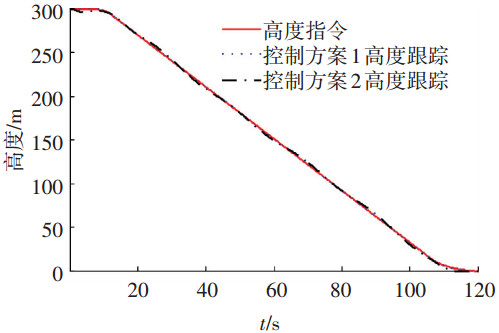
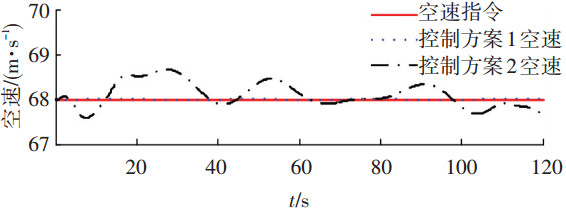
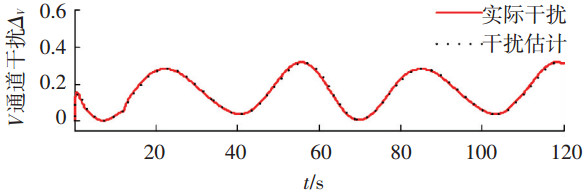
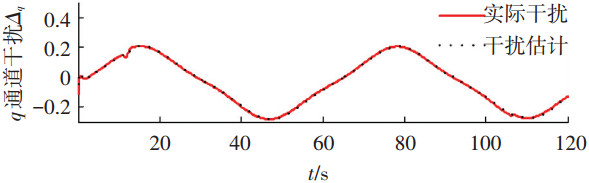
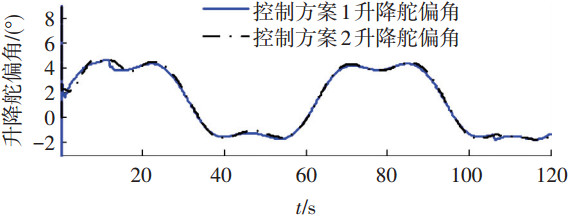
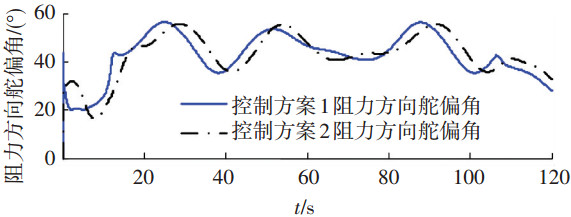
5.2 仿真结果分析

仿真结果如图 3~9所示，图 3，4为两种控制方案下无人机高度、空速跟踪曲线，图 5~7为控制方案1各通道干扰与干扰观测器的干扰估计.图 8, 9为两种控制方案升降舵与阻力方向舵偏角.控制方案1采用了观测器及L₂增益方法抑制干扰对着陆的影响，由图 5~7可知，各通道干扰估计与实际干扰曲线基本重合，滑模干扰观测器实现了对干扰的估计.从图 3，4可以看出，控制方案1无人机的高度和空速都很好地跟踪了指令，高度跟踪误差小于0.62 m，空速跟踪误差小于0.01 m/s，且无人机纵向着陆垂直接地速度为0.46 m/s，在允许的垂直接地速度范围内.从图 3，4可以看出，采用PID控制的控制方案2，无人机高度和空速跟踪误差较大，高度跟踪误差达到4.55 m，空速跟踪误差达到0.72 m/s，无人机垂直接地速度为1.58 m/s，而本文的飞翼布局无人机的允许垂直接地速度仅为0.8 m/s，由此可知，对于存在时变干扰的飞翼布局无人机纵向着陆控制系统，PID控制效果比较差.

综上所述，本文提出的基于干扰观测器和跟踪微分器的反步L₂增益纵向着陆鲁棒控制方案，抑制了干扰对控制系统的影响，无人机高度、空速都跟踪上了控制指令，垂直接地速度在允许的范围内，具有良好的着陆控制性能.

6 结论

1) 对于存在气动参数不确定和时变干扰影响的飞翼布局无人机纵向自动着陆控制问题，本文提出了一种基于观测器的反步L₂增益鲁棒控制方案.综合采用super twisting滑模干扰观测器和L₂增益方法抑制了复合干扰的影响，在反步控制设计中，采用跟踪微分器避免了传统动态面反步设计方法存在的脆弱性问题.

2) 在气动参数施加-30%的不确定并同时加入时变力矩干扰的情况下，飞翼布局无人机纵向自动着陆高度跟踪误差小于0.62 m，空速跟踪误差小于0.01 m/s，垂直接地速度为0.46 m/s，相对于传统的PID控制具有更好的着陆控制性能.