2. 哈尔滨工程大学 航天工程系, 15001 哈尔滨
2. Dept. of Astronautics Engineering, Harbin Engineering University, 150001 Harbin, China
升力式再入飞行器飞行距离远、机动能力强,可在短时间内实现对全球任意目标的精确打击,具有重要的军事意义,正受到世界各军事大国的关注.升力式再入飞行器由助推火箭助推至一定高度后分离,然后在大气层内进行滑翔飞行至目标点附近,最后下压以一定的弹道倾角对目标实行精确打击.在整个飞行全过程中,由于大气的存在,其环境极其复杂,要保证飞行器安全地到达目标上空,并实行对目标的精确打击,具有较大的难度和挑战性.为此,开展升力式再入飞行器全程三维自主制导方法具有重要意义和应用价值,其主要涉及再入段制导、下压段制导以及两段间的平稳过渡等.
目前航天飞机的再入段制导是反复经过工程实践检验,较为成熟的升力式再入制导方法[1],同时阿依华州立大学[2-4]和加利福尼亚大学[5-7]研究的再入制导方法也引起了众多学者的研究兴趣.对于下压段制导,自从1973年Kim等[8]首次在机动弹头的末端制导中引入落角约束以来,国内外的学者针对不同的应用背景,应用最优控制[9]、滑模控制[10]、自适应控制等控制理论提出了多种具有终端角度约束的导引律[11-15],而对于升力式再入飞行器全程制导方法至今没有出现过完整的研究文献.本文研究了一种能够满足再入约束、射程和航向角要求,以一定弹道倾角对目标实施精确打击的升力式再入飞行器全程三维自主制导方法,该方法由再入段制导、下压段制导以及两段间平滑过渡方式组成.
1 以能量为自变量的归一化再入运动数学模型升力式再入飞行器在再入过程中所具有能量不断减少,同时由于再入的起始和末端状态为给定的要求值,其对应的能量就为已知值,相比飞行时间为未知而言,能量是一个很好的自变量,在无需精确获得飞行时间的情况下就可积分再入运动方程.取再入过程中的能量E的表达式如下:

|
式中:V为再入飞行器相对于地球大气的速度;r为飞行器质心到地心的距离;μ为地球引力常数.
为了提高再入制导相关算法迭代计算的收敛性,需对再入飞行器的运动模型进行相应的归一化.
能量归一化的形式E为

|
式中:V为相对地球的归一化速度,r为归一化的地心距离.
在忽略地球自转和扁率的情况下,将E对归一化的时间τ求导可得
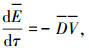
|
(1) |
式中D为归一化的阻力加速度.
根据式(1)再结合归一化的再入动力学模型,将对时间的导数变成对归一化能量的导数,最终得到数学模型为:
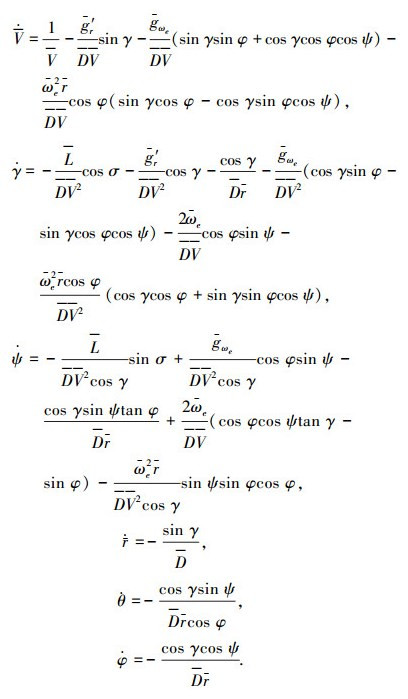
|
(2) |
式中: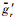
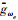
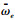
再入飞行器全程飞行过程中需要满足过程约束、控制约束以及相关的末端约束.
2.1 过程约束过程约束主要包括动压、法向过载、驻点热流约束以及拟平衡滑翔条件,对应的归一化模型分别为:

|
式中:q为归一化的动压;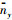
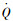
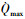
控制约束为:
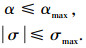
|
式中:α为攻角;αmax、σmax分别为最大攻角、最大倾侧角.
2.3 末端约束末端约束主要有再入段末端约束和下压段末端约束,其中再入段末端约束为:
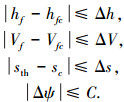
|
式中:hf、Vf、sth分别为再入段末端高度、速度以及距目标点的距离;hfc、Vfc、sc分别为要求的再入末端高度、速度以及距目标点距离的约束值;Δh、ΔV、Δs分别为再入末端高度误差、速度误差以及距目标点距离误差的允许值;Δψ为末端航向角偏差; C为其允许值.
下压段末端约束为:
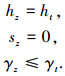
|
式中:hz、sz、γz分别为下压段末端高度、与目标点的距离、飞行路径角;ht为目标点高度;γt为要求的弹道倾角值.
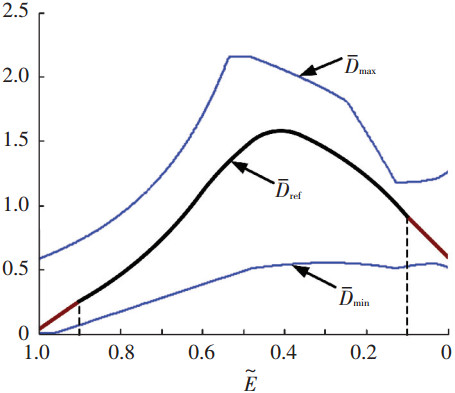
3 再入段制导方法 3.1 轨迹规划方法轨迹规划基于阻力加速度剖面设计,阻力加速度剖面采用再入走廊上下边界内插得到,如图 1所示.
|
图 1 参考阻力加速度剖面示意 |
阻力加速度剖面的具体设计形式为
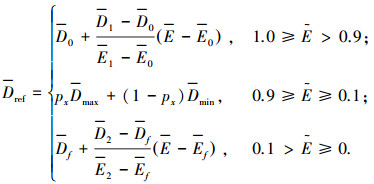
|
(3) |
式中:D0、Df分别为归一化的起始和末端的阻力加速度;E0、Ef分别为归一化的起始和末端的能量;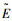
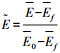
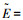
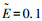
由于轨迹规划采用阻力加速度剖面设计,阻力加速度剖面又由再入走廊上下边界内插得到,所以阻力加速度剖面一定在再入走廊内,可以有效满足再入过程中的过程约束.同时再入段末端的阻力加速度和能量能够有效保证末端的速度和高度,因此再入段末端还需满足到目标点距离以及航向角约束.满足两个约束至少需要两个可以调节的参数,内插值系数px可以作为一个调节参数,为此倾侧角至少需要进行一次反转,将反转点归一化的能量作为一个调节的参数.但如果倾侧角只进行一次反转,当倾侧角反转完成后,能够调节的参数仅剩内插值系数px,无法再同时满足到目标点距离以及末端航向角两约束的要求,参考轨迹不能较好地进行更新.为此倾侧角进行两次反转,将两次反转点归一化的能量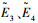
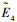

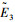
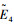
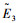
1) 给出
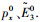
2) px0给定后,由式(3)确定阻力加速度剖面,也即不同的E对应的Dref值唯一确定,而E和Dref又由r和V决定,为此采用迭代法求得r、V,获得不同E对应的r后采用差分法可以求得r对E的导数
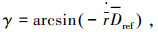
|
(4) |
同理,将不同E对应的γ采用差分法获得γ对E的导数
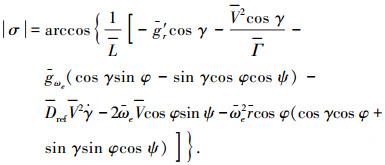
|
(5) |
3) 确定倾侧角符号:
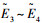
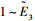
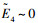
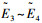
4) 获得不同E下的Dref、r、V、γ以及σ后,积分求得末端点的经纬度和航向角为:
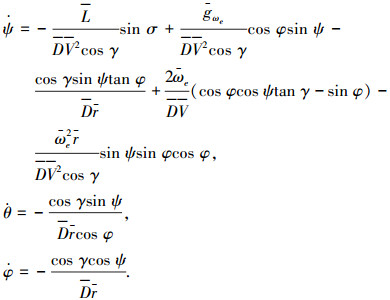
|
(6) |
5) 根据求得的末端点航向角和经纬度,可以得到航向角偏差和与目标点的距离,再结合相应的约束,采用牛顿迭代法可以迭代求解获得满足约束的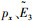
由轨迹规划可以获得攻角和倾侧角指令,但由于在轨迹规划时存在一定的假设和简化,如果飞行器按照轨迹规划中的攻角和倾侧角指令进行飞行,则跟踪不上规划出的轨迹剖面,有可能使飞行器不满足过程约束和终端约束,为此需要对攻角指令和倾侧角指令进行修正.为了使跟踪方法简单容易实现,攻角采用给定的攻角剖面值,只对倾侧角指令进行修正.
攻角指令αcmd为
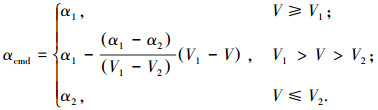
|
式中:α1、α2、V1、V2分别为根据轨迹分析所取得定值.
倾侧角指令σcmd为
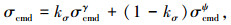
|
且有:

|
式中:sgn(σref)为由轨迹规划获得的倾侧角的符号;kp、kd、ki分别为常数;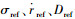
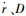
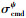
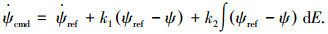
|
(7) |
式中:k1、k2分别为常数;
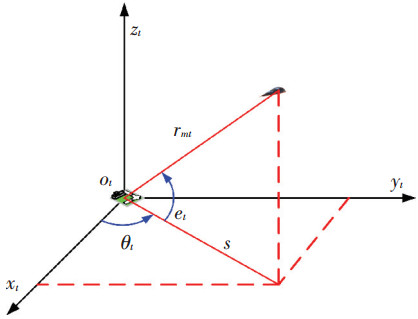
下压段制导的目的主要是导引飞行器以一定的弹道倾角对目标进行精确打击,并且不过多地依赖于目标的信息.为了较好地对问题进行描述,如图 2所示在目标点建立固连坐标系otxtytzt.坐标原点ot为目标点,otxt、otyt轴均在水平面内,分别指向东向和北向,otzt轴与otxt、otyt轴组成右手坐标系.
图 2中rmt为再入飞行器到目标点的距离, s为再入飞行器在otxtyt面上的投影到目标点的距离, θt为再入飞行器与目标点的方位角,与otxt轴逆时针方向的角度为正,取值范围为-π≤θt<π, et为再入飞行器与目标点的高低角,在otxtyt平面上方为正,下方为负,取值范围为-π/2≤et≤π/2.
|
图 2 目标点的固连坐标系示意 |
若飞行器要以一定的弹道倾角精确命中目标,则需满足:

|
式中:xf、yf、zf分别为飞行器在弹道终端相对目标点固连坐标系otxtytzt上3个方向的分量; Γf为给定的弹道倾角约束.
则根据飞行器当前点的经度λ、纬度φ和地心距r可以得到飞行器在目标点固连坐标系的坐标x、y、z为
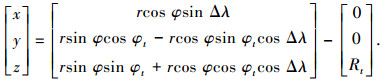
|
式中:φt为目标点纬度;Δλ=λ-λt;Rt为目标点处的地心距.
则飞行器相对目标点固连坐标系的位置变化率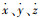
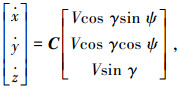
|
式中V为飞行器相对地球的速度,且有

|
则飞行器在目标点固连坐标系上的方位角θt可通过以下方法求得:
1) 当x>0时,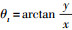
2) 当x<0时,
3) 当x=0时,如果y>0,θt=π/2;如果y<0,θt=-π/2.通过上述步骤后,若θt≥π,则θt=θt-2π.
对于方位角θt的导数,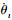
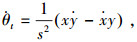
|
式中
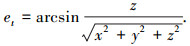
|
(8) |
对于高低角et的导数,
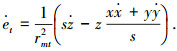
|
取如下制导指令:
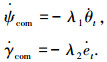
|
式中:λ1、λ2分别为制导参数.通过理论分析得到:
1) 对于任意的V,若λ1>1和λ2>1同时成立,则必有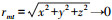
2) 对于任意的V,若λ1>2与λ2>2成立,则飞行器最终将以直线形式不断逼近目标,并且末端满足θt+ψ=-π/2和et+γ=0.
通过上述分析可以得到相应的制导流程如图 3所示.
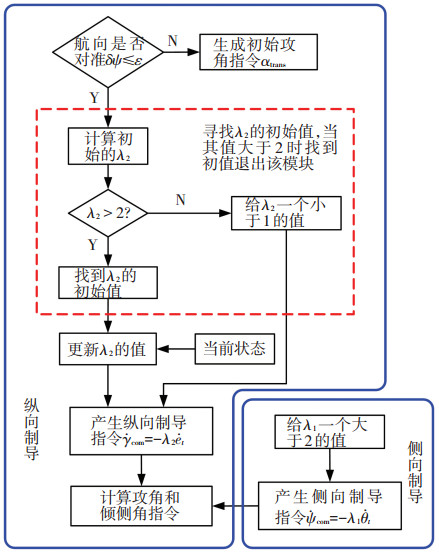
|
图 3 自适应制导流程 |
图 3中δψ可计算为
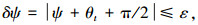
|
ε为给定的小量.
λ2的初值、更新计算公式为:

|
式中κ2为给定参数.
当获得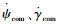
1) 由式(9)计算Lcom为

|
(9) |
式中: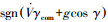
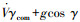
2) 由式(10)计算得到CLcom为
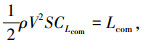
|
(10) |
式中S为飞行器的参考面积.
3) 得到CLcom,根据气动参数,利用牛顿迭代即可得到αcom,当αcom达到极值限制时,就取相应的极值.
4) 通过式(11)获得σcom,当σcom达到极值限制时,就取相应的极值为
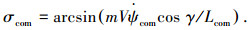
|
(11) |
通过再入段制导方法可以获得再入段的攻角和倾侧角指令,从而导引飞行器在满足动压、过载、气动热、射程等约束的基础上顺利到达目标点上空;通过下压段制导方法可以获得下压段的攻角和倾侧角指令,从而导引飞行器以一定的弹道倾角精确命中目标.但由于再入段和下压段的环境、制导需求以及制导方法不同,必然导致再入段和下压段衔接点处各自生成的攻角和倾侧角指令不一致,为此为保证飞行器再入段和下压段的平稳过渡,需要以再入段和下压段衔接点为起点对下压段的攻角和倾侧角进行平稳过渡.
通过自适应制导算法可以看出:下压段初期需要使δψ≤ε,为此可以采用最大升阻比攻角使飞行器有较大的机动能力,来尽快满足δψ≤ε,但对倾侧角没有特殊要求,其直接由指令式(11)生成.为此,再入段和下压段平稳过渡的主要问题就是,使再入段末端时刻的攻角α0和倾侧角σ0,分别平稳过渡为最大升阻比攻角α*和下压段产生的倾侧角指令σcom·αtrans、σtrans分别采用式(12)、(13)进行平稳过渡:
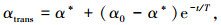
|
(12) |
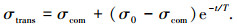
|
(13) |
式中:t为下压段的飞行时间,下压段开始时刻t=0;T为末制导的时间常数,为一给定值.
从式(12)、(13)可以看出:在下压段开始时刻攻角和倾侧角分别为α0和σ0,与再入段末端相同,不会出现跳点;同时随着时间的增加e-t/T接近于零,攻角和倾侧角逐渐过渡为α*和σcom.
6 仿真分析为了验证本文研究的再入飞行器全程三维自主制导方法的适应性和制导精度,取表 1中的初始条件、表 2中的约束条件、表 3中的干扰进行蒙特卡洛打靶仿真,仿真过程中当飞行器未飞过第1个反转点时每100 s重新规划一次轨迹,当飞过第1个反转点后每20 s重新规划一次轨迹.相应的仿真结果如图 4~9所示.
| 表 1 仿真初始条件 |
| 表 2 约束条件 |
| 表 3 仿真偏差量 |

|
图 4 再入段末端高度 |

|
图 5 再入段末端速度 |
|
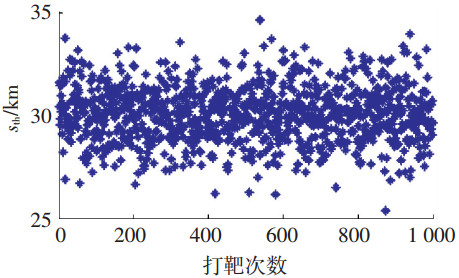
图 6 再入段末端距目标点的距离 |
|
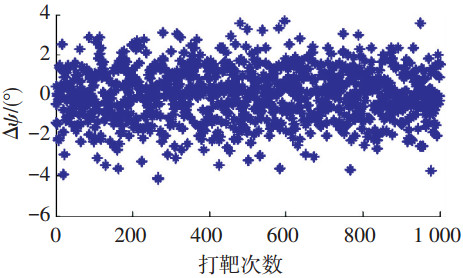
图 7 再入段末端航向角误差 |

|
图 8 下压段末端距目标点的距离 |
|
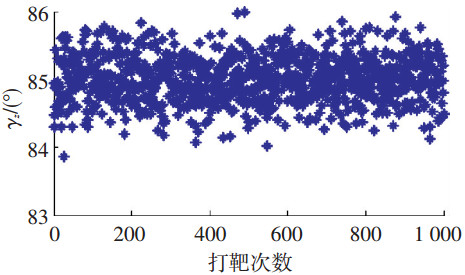
图 9 打击的弹道倾角 |
从图 4中可以看出再入段末端高度在30 km左右,最大偏差为2 km,满足再入段末端高度约束;从图 5中可以看出再入段末端速度在900 m左右,最大偏差为100 m,满足再入段末端速度约束;从图 6中可以看出再入段末端距目标点的距离为30 km左右,最大偏差为4 km,满足再入段末端距离约束;从图 7中可以看出再入段末端航向角的最大误差为4°,满足再入段末端航向角约束;从图 8中可以看出,该制导方法对目标打击的偏差均小于10 m;从图 9中可以看出打击的弹道倾角在85°左右,最大偏差为1.3°.
7 结论1) 本文给出的再入段制导方法,基于再入走廊设计,最多只需调节两个参数即可获得满足再入和末端约束的再入轨迹,轨迹规划运算量少,可以实现在线规划,满足自主制导要求.
2) 本文研究的下压段制导,基于传统的比例导引形式,但实时更新制导参数,能够满足以规定的弹道倾角对目标实施精确打击.
3) 通过再入段和下压段控制指令间的平滑过渡实现了再入飞行器全程三维自主制导方法,其打击偏差小于10 m,弹道倾角偏差小于1.3°.
| [1] |
ZIMPFER D, HATTIS P, RUPPERT J, et al. Space shuttle gn & c development history and evolution[C]//Proceedings of the AIAA SPACE 2011 Conference and Exposition. California: AIAA, 2011.
|
| [2] |
LU Ping. Asymptotic analysis of quasi-equilibrium glide in lifting entry flight[J]. Journal of Guidance, Control, and Dynamics, 2006, 29(3): 662-670. |
| [3] |
LU Ping. Entry trajectory optimization with analytical feedback bank angle law[C]//Proceedings of the AIAA Guidance, Navigation and Control Conference and Exhibit. Hawaii: AIAA, 2008.
|
| [4] |
LU Ping, XUE Songbai. Rapid generation of accurate entry landing footprints[J]. Journal of Guidance, Control, and Dynamics, 2010, 33(3): 756-767. |
| [5] |
WAGNER J J, WILHITE A W, STANLEY D O, et al. An adaptive real time atmospheric prediction algorithm for entry vehicles[C]//Proceedings of the 3rd AIAA Atmospheric Space Environments Conference. Hawaii: AIAA, 2011.
|
| [6] |
SARAF A, LEAVITT J A, CHEN D T, et al. Design and evaluation of an acceleration guidance algorithm for entry[C]//Proceedings of the AIAA Guidance, Navigation, and Control Conference and Exhibit. Austin: AIAA, 2003.
|
| [7] |
XUE Songbai, LU Ping. Constrained predictor-corrector entry guidance[J]. Journal of Guidance, Control, and Dynamics, 2010, 33(4): 1273-1281. |
| [8] |
KIM M, GRIDER K V. Terminal guidance for impact attitude angle constrained flight trajectories[J]. IEEE Transactions on Aerospace and Electronic Systems, 1973, 9(6): 852-859. |
| [9] |
王铀, 赵辉, 翁兴伟. 带攻击角度约束的机动目标SUAV三维末制导律研究[J]. 电光与控制, 2012, 19(9): 8-12. |
| [10] |
孙未蒙, 郑志强. 一种多约束条件下的三维变结构制导律[J]. 宇航学报, 2007, 28(2): 344-349. |
| [11] |
LU Ping, DOMAN D B, SCHIERMAN J D. Adaptive terminal guidance for hypervelocity impact in specified direction[C]//Proceedings of the AIAA Guidance, Navigation, and Control Conference and Exhibit. San Francisco: AIAA, 2005: 2108-2129.
|
| [12] |
YURI Ulybyshev. Terminal guidance law based on proportional navigation[J]. Journal of Guidance, Control, and Dynamics, 2005, 28(4): 821-824. |
| [13] |
ASHWINI R, DEBASISH G. Impact angle constrained interceptionof stationary targets[J]. Journal of Guidance, Control, and Dynamics, 2008, 31(6): 1816-1821. |
| [14] |
HU Zhengdong, CAI Hong. An adaptive proportional guidance law against ground stationary target[C]//Proceedings of the 2nd International Symposium on Systems and Control in Aerospace and Astronautics. Shenzhen: IEEE, 2008: 1-5.
|
| [15] |
蔡洪, 胡正东, 曹渊. 具有终端角度约束的导引律综述[J]. 宇航学报, 2010, 31(2): 315-323. |
 2016, Vol. 48
2016, Vol. 48





