自从1852年法国工程师亨利·吉法尔[1]成功制造世界上首架动力驱动的可驾驶飞艇后,飞艇很快就迎来了它的黄金岁月. 各国重视飞艇在军事中的应用,在第一次世界大战前后,德国就建立了用于海上巡逻、远程轰炸、空中运输等军事活动的飞艇部队[2-3].但是1937年的“兴登堡”号空难[4]阻碍了飞艇进一步的应用与发展.随着材料科学等相关学科的发展,提高飞艇的各项性能指标成为了可能,尤其在无线通信系统和高分辨率对地观测系统等应用中的广阔前景,再次激发了人们的兴趣,飞艇平台获得了它的“第二次生命”[5].
飞艇艇体有柔性结构、半刚性结构以及刚性结构3种结构形式[6-8],不同的结构形式对应于不同的应用目的与飞行环境.其中,柔性结构的艇体由单纯的充气囊体构成;而半刚性结构以及刚性结构的艇体则由充气囊体与刚性结构体系组成刚柔混合结构体系,其力学协调关系更为复杂.
无论飞艇艇体为何种结构形式,把握充气囊体的力学行为特征是飞艇结构体系设计的一个重要基础.尤其是对于体量较大的飞艇结构,其结构行为的变化还将表现在对气动特性[9-10]以及浮重平衡的影响.对于近十多年来国内外所关注的平流层飞艇,利用刚性结构体系的“笼子”效应,可以有效解决平流层飞艇下降过程中的囊体进气难的问题,避免出现明显的超冷超热效应,但是“笼子”行为的构成也依赖于充气囊体在不同压差条件下对其力学特征的准确把握.本文利用经典力学理论及商用有限元软件ABAQUS,对典型飞艇外形囊体进行数值计算,对计算结果进行比较分析,探讨结构抗力指标(材料弹性模量、泊松比、囊体长度以及囊体长细比)对飞艇充气囊体变形的影响,以便为平流层飞艇的设计提供参考.
1 影响因素的分类通常可以根据荷载效应(S)和结构抗力(R)两个指标对变形的影响因素进行分类,见表 1.
| 表 1 两种指标下的影响因素 |
本文使用的飞艇平台囊体的长细比为2.65,外形曲线为非标准三叶玫瑰线的一枝.在平面X-Y内投影曲线为

|
式中a为飞艇长度,本模型中a=160 m.
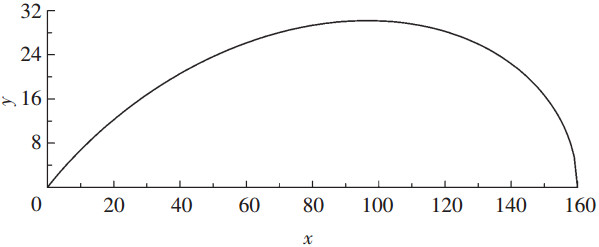
飞艇囊体母线如图 1所示.
|
图 1 飞艇囊体母线 |
用Matlab计算的飞艇囊体的几何特性参数见表 2.
| 表 2 囊体几何参数 |
对悬浮于空气中的飞艇进行有限元静力分析计算时,不能把飞艇处理为全自由度结构.由于有限元静力分析的计算模型中应无机构和刚体运动[11-12],而全自由度结构刚度矩阵奇异,数值计算无法进行.因此在数值分析中,通常可以采用以下两种方法计算悬浮飞艇的静力问题.
1) 在ANSYS中可以利用惯性释放(inertia relief)技术对完全无约束的飞艇平台进行静力分析.惯性释放指用结构的惯性力来平衡外力.尽管结构没有约束,分析时仍假设其处于一种“静态”的平衡状态.
利用惯性释放技术进行数值计算的过程如下[13].
a) 计算结构所受合力以及相对于结构中心的外力矩,设为FT(t)、Fr(t).
b) 根据平衡条件,在结构上施加平动加速度及转动加速度为
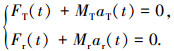
|
式中:FT(t)、Fr(t)分别为t时刻结构所受的平动力和转动力; aT(t)、ar(t)分别为t时刻结构相对于重心的平动加速度和转动加速度.
c) 根据新的外力,重新计算结构受力.
2) 用ABAQUS进行静力计算时,可以通过施加一定的约束条件使有限元分析能进行下去.一种常用的做法是,用纵截面(X-Y)面剖切囊体,在截面处施加Z向约束,飞艇头部施加全约束,尾部只允许X方向的位移.考虑吊挂荷载时,也可以在吊挂处施加全约束.
惯性释放的方法忽略了重力荷载效应的影响,会产生较大误差.因此本文在使用ABAQUS作数值计算时,使用第2种方法处理约束.
3 算例验证飞艇充气囊体是典型的大曲率充气膜结构,囊体头锥、尾锥曲率较大,对于该类充气膜结构,很难通过解析的方法求解出其环向应力的精确值.
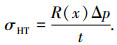
|
(1) |
式中:σHT为环向应力理论值;R(x)为截面半径; Δp为压差; t为膜材厚度.
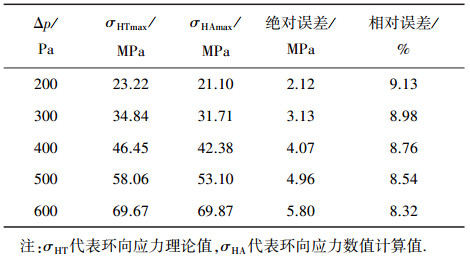
分别用式(1)和有限元软件ABAQUS,计算上述三叶玫瑰线形囊体在零度攻角下200、300、400、500、600 Pa纯压差下囊体环向应力最大值.材料厚度0.000 264 m,材料弹性模量8 GPa.计算结果见表 3.
| 表 3 环向应力理论值与数值计算值的对比(三叶玫瑰线形) |
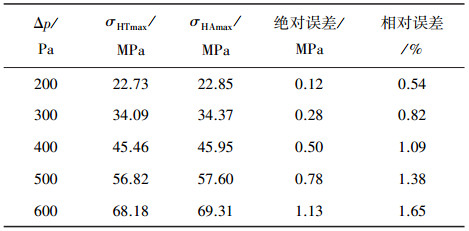
式(1)是圆管形充气膜结构的环向应力解析值.为消除由于环向应力近似对计算带来的影响,分别用式(1)和ABAQUS计算长160 m、长细比2.67的充气圆管(图 2),计算结果见表 4.计算表明,在200~600 Pa内,相对误差不超过1.7%.理论与数值结果吻合的较好.

|
图 2 充气圆管 |
| 表 4 环向应力理论值与数值计算值的对比(圆管形) |
综上分析,对于大曲率充气膜结构,若想仅通过理论推导来获取解析解并不现实,即使通过简化获取了解析解,由于简化而引起的误差也将较大.数值工具是计算大曲率充气膜结构的有效工具,其相对误差不到1.7%,数值解和理论解吻合的较好.
4 主要抗力指标对变形的影响 4.1 材料弹性模量和泊松比对囊体变形的影响弹性模量和泊松比是膜材最重要的两个力学性能指标,也是两个重要的结构抗力指标.如何选择合适的材料弹性模量和泊松比是飞艇结构设计的重要内容.
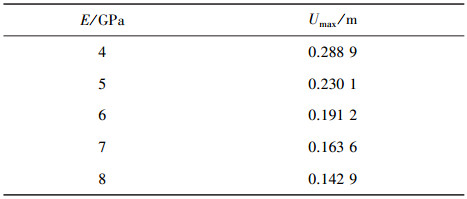
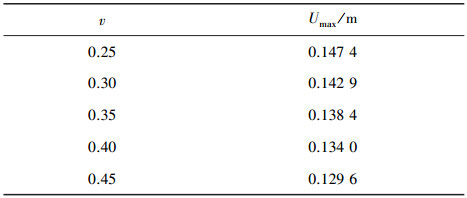
目前已知可用于平流层飞艇囊体膜材的弹性模量最大值在8~9 GPa,选择6.0、6.5、7.0、7.5、8.0 GPa这5个弹性模量值,计算各弹性模量下的囊体最大变形量以探究弹性模量对长度方向变形的影响,计算结果见表 5.膜材的泊松比一般为0.2~0.5,选择0.25、0.30、0.35、0.40、0.45这5个泊松比值,计算各泊松比下囊体最大变形量,计算结果见表 6.
| 表 5 各弹性模量下囊体最大变形量(L=160 m, p=400 Pa, ν=0.3) |
| 表 6 各泊松比下囊体最大变形量(L=160 m, p=400 Pa, E=8 GPa) |
计算结果表明:弹性模量与最大变形量曲线呈反比例,如图 3所示.当弹性模量由4 GPa开始,每增加一个1 GPa,增加到8 GPa时,变形分别减小0.058 8、0.038 9、0.027 6、0.020 7 m.随着弹性模量的增大,曲线斜率的绝对值不断减小,弹性模量对变形的影响减弱.泊松比与变形关系曲线呈直线,变形随泊松比的增大而减小,泊松比每增大0.05,变形减小约0.004 5 m.从图 3可见,弹性模量对变形的影响比泊松比的影响更加明显.

|
图 3 不同泊松比和弹性模量下的囊体变形量 |
在弹性模量、泊松比两个抗力指标中,弹性模量对变形的影响是非线性的,泊松比对变形的影响是线性的,弹性模量对变形的影响强于泊松比对变形的影响.因此,在飞艇膜材选择时,应选择弹性模量和泊松比均较大的膜材,但当弹性模量、泊松比同时达到较大时,首选弹性模量较大的膜材.
4.2 囊体长度对囊体变形的影响相同材料弹性模量和长细比的情况下,对比120、160、200、240 m这4种囊体尺度在同一工况下的最大变形,数值计算结果见表 7.
| 表 7 各长度下囊体最大变形量(E=8 GPa, p=400 Pa) |
对比数值计算变形量分布云图,发现变形变化趋势相似,但数量值却相差很大,变形量并不与艇体长度成正比关系.如,240 m艇体最大绝对变形量比120 m艇体最大绝对变形量大4倍左右.各长度下的变形量有以下关系:
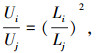
|
(2) |

|
(3) |
式中:i, j=1, 2, 3, 4.
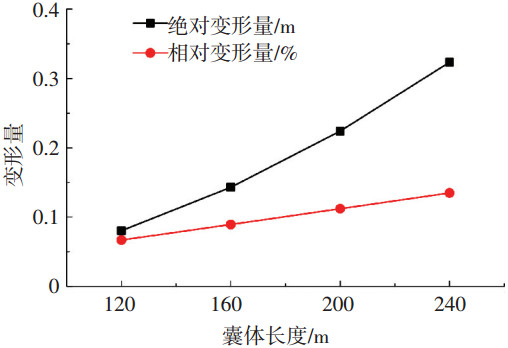
对数值结果的分析整理,得出如下结论:囊体长度变为原来的n倍时,绝对变形量变为原来的n2倍,相对变形量U/L是原来的n倍,如图 4所示.
|
图 4 囊体长度—囊体最大变形量曲线 |
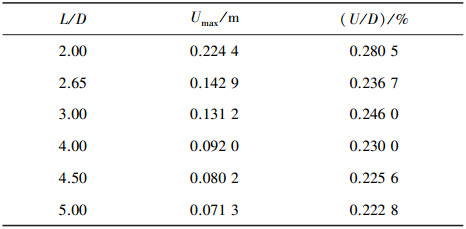
为考察长细比对变形的影响,对比一组不同长细比下的充气囊体在相同工况下的囊体变形.选择囊体长度为160 m,材料弹性模量、密度均相等,计算在长细比为2.00、2.65、3.00、4.00、4.50、5.00这6种情况下的囊体绝对变形量和相对变化量.长细比为2、3、4、5的囊体外形如图 5所示,各长细比囊体变形计算结果见图 6及表 8.

|
图 5 不同长细比下的囊体外形 |
|
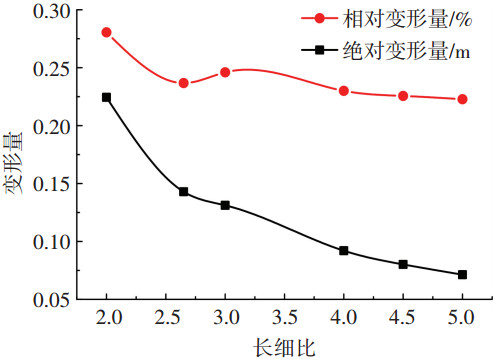
图 6 长细比—囊体最大变形量曲线 |
| 表 8 各长细比下囊体最大变形量(L=160 m, E=8 GPa) |
在图 6中,长细比—绝对变形量曲线随长细比增大而减小,但长细比—相对变形量曲线在长细比为3~4的区段出现了极值点.这是因为囊体变形包含了由外荷载引起的弹性变形和与结构外形有关的结构变形,属于非弹性变形.对于如图 5所示的不同长细比的充气膜结构,长细比越大,非弹性变形越小.因此,即使各长细比的囊体在不同的外荷载作用下发生等量的弹性变形,但总的变形量也不会相等,长细比大的总变形小,两种变形量共同决定总变形量.该极值点的出现反映了弹性变形和结构变形各自随压差变化曲线是非线性的.
由图 6可知,长细比2~3区段,绝对变形量、相对变形量曲线斜率均较大,该区段长细比对变形影响十分明显;长细比3~4区段绝对变形量、相对变形量曲线斜率较前2~3区段明显偏小,但又较4~5区段明显偏大;长细比4~5区段,绝对变形量曲线接近直线,相对变相量曲线平缓,近似水平线.
另外,值得注意的是:飞艇是依靠浮升气体提供浮升力的,而浮升力与飞艇体积正相关.在飞艇结构设计时,给定飞艇有效荷载,则飞艇囊体的体积V也可以近似估算出来,在V为定值的情况下,长细比L/D大意味着L较长.较大的长度无论是对于飞艇空气静力学、动力学、飞行控制,还是对于飞艇的制造,都是不利的.美国《Airship Design Criteria》(NO.FAA-P-8110-2)所用的有关飞艇力学计算的长细比不大于6也是基于这个考虑的.
因此,在飞艇结构设计时,长细比应位于相对变形量曲线为近似水平直线的4~5区段,尽可能使长细比接近4以避免囊体长度过长.
5 结论1) 材料刚度与最大变形量关系曲线呈反比例,泊松比与最大变形量曲线为正比例,弹性模量对变形的影响强于泊松比.
2) 同种工况条件下,囊体长度变为原来的n倍时,绝对变形量变为原来的n2倍,相对变形量变为原来的n倍.
3) 长细比4~5区段时相对变形量曲线近似水平直线,选择长细比为4~5并尽可能接近4对减小相对变形是有利的.
| [1] |
甘晓华, 郭颍. 飞艇技术概论[M]. 2005.
|
| [2] |
RYAN, D E. The airship's potential for intertheater and intratheater airlift[R]. Alabama: Air University School of Advanced Airpower Studies United States Air Force Maxwell Air Force Base, 1992.
|
| [3] |
GERKRN L C. Airships:history and technology[M]. Chula Vista, California: American Scientific Corporation, 1990: 464.
|
| [4] |
ARCHBOLD R. Hindenburg:an illustrated history[M]. Toronto: Viking Studio/Madison Press, 1994.
|
| [5] |
WILSON J R. A New era for airship[J]. Aerospace America, 2004, 42(5): 27-31. |
| [6] |
KHOURY G A, GILLET J D. Airship technology[M]. Cambridge, UK: Cambridge University Press, 1999.
|
| [7] |
LIAO L, PASTERNAK I. A review of airship structure research and development[J]. Progress in Aerospace Science, 2009, 45(4/5): 83-96. |
| [8] |
杨艳初, 王生, 姜鲁华. 飞艇总体构形新概念设计[C]//2007年中国浮空器大会论文汇编. 北京: 中国浮空器大会论文集, 2007: 39-43.
|
| [9] |
LIU Jianmin, LU Chuanjing, XUE Leiping, et al. Coupling computation of the flow field and the large deformation of membrane structure of stratosphere airships[J]. Journal of Hydrodynamics, 2008, 20(4): 536. DOI:10.1016/S1001-6058(08)60091-8 |
| [10] |
LI Yuwen, NAHON M, SHARF I. Airship dynamics modeling:a literature review[J]. Progress in Aerospace Sciences, 2011, 47(3): 217-239. DOI:10.1016/j.paerosci.2010.10.001 |
| [11] |
LIN Liao. A Study of Inertia Relief Analysis[C]//Pro-ceedings of the 52nd AIAA/ASCE/AHS/ASC Structures, Structural Dynamics and Materials Conference. Denver, Colorado: AIAA, 2011: 1-10.
|
| [12] |
张少雄, 杨永谦. 惯性释放在油船结构强度直接计算中的应用[J]. 船海工程, 2004(4): 4-6. |
| [13] |
刘平. 大体积柔性充气结构流固耦合性能分析方法研究[D]. 上海: 上海交通大学, 2014.
|
| [14] |
杨留义. 囊体结构设计及其气弹特性计算分析[D]. 哈尔滨: 哈尔滨工业大学, 2012.
|
| [15] |
黄迪, 赵海涛, 邱野, 等. 平流层飞艇蒙皮强度建模与仿真研究[J]. 计算器仿真, 2013, 30(1): 150-153. |
 2016, Vol. 48
2016, Vol. 48