2. 空军工程大学 装备发展与运用研究中心, 710051 西安
2. Research Center of Equipment Development and Application, Air Force Engineering University, 710051 Xi'an, China
FH通信具有抗干扰、抗侦收等诸多优点,已逐渐成为军事通信领域重要的反截获技术手段,在现代战争中应用广泛并发挥了巨大威力[1].FH信号侦察研究一直是通信侦察和无线频谱监测等领域的热点问题.
信号波达方向(DOA)是通信侦察中非常关键的参数,其对FH网台分选和信号确认等任务具有重要支撑作用[2].文献[2-4]将FH信号视为窄带信号进行DOA估计,所提方法无法适用于短波和超短波环境(跳频带宽与射频中心频率的比值较大),也不能用于欠定条件(信源数大于天线数);文献[5-7]提出了基于空间时频分布的FH信号一维DOA估计方法,可实现欠定估计,但无法给出俯仰角信息.极化状态是电磁波的固有属性,当阵列系统引入极化信息时,其导向矢量的空间维度加倍,协方差矩阵进行子空间分解亦可多一个自由度,利于提高空间分辨力(DOA估计精度)[8].此外,极化信息本身对于辅助信号分选和目标识别同样具有重要作用[9].可见,极化结合信源方位能够显著提高FH信号辨识度,进而在FH网台分选和信号识别等应用中发挥重要作用.因此,对FH信号二维波达方向(2D-DOA)和极化参数进行联合估计意义重大, 然而,目前鲜有关于该问题的研究报道.文献[10]给出一种基于电磁矢量天线的方法,但仅能估计5个以内的FH信号.鉴于欠定情况在实际环境中经常出现,故亟待寻求适用于欠定条件的FH信号2D-DOA与极化参数联合估计方法.
本文用正交电偶极子构造L型极化敏感阵列,首先,建立FH信号的阵列数据模型,并采用空间极化时频分布[11](spatial polarimetric time frequency distributions,SPTFD)与其线性时频扩展形式SPSTFT分别对FH信号各hop的2D-DOA和极化参数进行联合估计;其次,研究各hop的SPTFD/SPSTFT矩阵构造方法.理论分析证明,所提方法无需高维参数寻优与配对;最后,通过3组仿真实验验证了算法的有效性,并根据实验结果重点探讨了算法在欠定条件和频率碰撞发生时的适用性.
1 FH信号的极化敏感阵列数据模型设FH信号sn(t)的跳周期为Tn,在观测时间Δt内共包含K个跳,第k(k=1, 2, …, K)跳载频为ωnk,起始跳持续时长为Δt0n,则sn(t)可表示为[1]
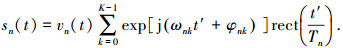
|
式中:t′=t-(k-1)Tn-Δt0n;vn(t)为sn(t)的基带复包络;φnk为第k跳的初相;rect(t)为单位矩形窗.
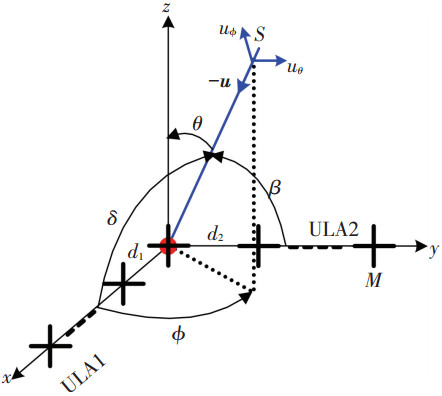
阵列结构如图 1所示,x轴和y轴方向的M元均匀线阵分别定义为ULA1和ULA2,阵元间距分别为d1、d2,满足:max(d1, d2)<c/2fmax,fmax为侦测频段内FH信号载频的最大值.定义坐标原点的阵元为参考阵元.FH信号为宽带信号,如果分析某一hop,可简化为窄带模型.假设极化参数为(γ, η)(γ∈[0, π/2]为极化辅角,η∈[0, 2π]为极化相位差)的窄带平面波S以俯仰角θ∈[0, π/2)和方位角ϕ∈[0, 2π)沿单位方向矢量-u入射,则极化矢量表示为[12]

|
(1) |
|
图 1 L型正交电偶极子阵列 |
式中:γy、γz分别为沿y轴和z轴方向的电场分量.将图 1中信源S与x、y轴的夹角δ、β分别作为新的俯仰角和方位角定义,两种角度之间的转换关系为
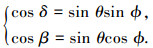
|
(2) |
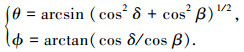
|
(3) |
式中:δ∈[0, π), β∈[0, π).由式(2)可知,经典的角度定义,俯仰角和方位角耦合在一起,无法单独求解,采用新的角度定义可实现俯仰角、方位角的独立估计[13].本文理论阐述部分将δ、β称为俯仰角和方位角;将θ、ϕ称为原始俯仰角和原始方位角.假设阵元增益为1,并忽略单阵元共点接收通道不一致及互耦影响,则ULA1对信源S的导向矢量为
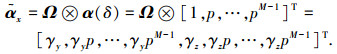
|
(4) |
式中:p=e-j2πd1cos(δ)/λ,λ=c/f(其中c为光速,f为瞬时频率)为信号波长;“⊗”为Kronecker积.同理,子阵ULA2的导向矢量为
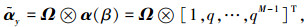
|
(5) |
式中q=e-j2πd2cos(β)/λ.阵列对信源S的导向矢量为
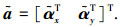
|
若存在N个FH信号s1~sN,在某个频率驻留时间(相邻跳时刻之间时间段)内,阵列流型矩阵为
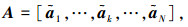
|
则阵列快拍数据矩阵为
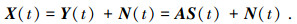
|
(6) |
式中:S(t)为信源的N×1维数据矢量;N(t)为阵列的4M×1维噪声数据矢量.
2 FH信号各hop的SPTFD/SPSTFT矩阵构造基于阵列快拍数据X(t),提取FH信号各hop时频点构造其SPTFD矩阵是估计2D-DOA和极化参数的基础.但构造SPTFD矩阵的时频分布计算次数正比于接收通道数平方,难以满足一些快速估计场合对于实时性的需求;此外,常规二次型时频分布存在交叉项干扰,不利于提取各hop自项时频点,影响算法性能.
2.1 SPTFD及其线性时频扩展形式SPSTFT 2.1.1 SPTFD的定义[11]对于信号x1(t)和x2(t),离散时间形式的Cohen互时频分布为
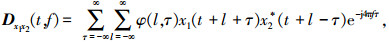
|
其中φ(l, τ)为核函数.SPTFD矩阵定义为
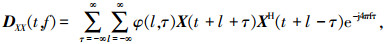
|
(7) |
式中, 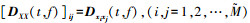

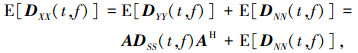
|
式中E[·]代表求期望运算.E[DXX(t, f)]与流型矩阵A具有相同的子空间特性.为保证E[DXX(t, f)]满秩,实际中一般通过提取关注信号的多个自项时频点并对时频点进行联合对角化或平均处理来估计E[DXX(t, f)].
2.1.2 空间极化短时傅里叶变换(SPSTFT)相比于Cohen分布,STFT计算量小、无交叉项干扰,实际中FH信号出现频率碰撞的概率很小,无需借助SPTFD矩阵的多源处理能力,因此在要求快速估计场合,可将Cohen分布用STFT替代.极化敏感阵列信号的STFT形式为

|
(8) |
式中,g(t)为窗函数.以STFTxi(t, f)为元素构造SPSTFT矩阵,结合式(6)有
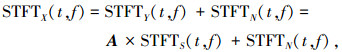
|
(9) |
对式(9)求期望,得
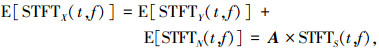
|
(10) |
由式(8)~(10)可见,SPSTFT矩阵保留了信源的空域和极化域特征信息,且构造SPSTFT矩阵的计算量显著低于SPTFD矩阵.
2.2 组合时频分布及SPSTFT/SPTFD矩阵构造 2.2.1 SPWVD&WVD组合时频分布Wigner-Ville分布(WVD)是时频分布的基础形式,具有理论上最佳的时频分辨性能.但FH信号是典型的多分量信号,其WVD结果存在严重交叉项干扰,导致难以提取自项时频点.平滑伪WVD(SPWVD)经过时、频域两次平滑,在交叉项抑制、时频聚焦性和抗噪能力3方面取得了很好平衡.本文将WVD和SPWVD进行组合,给出一种新的适合于FH信号的时频分析方法SPWVD&WVD.将参考阵元的SPWVD、WVD结果分别记为SPWVDx1x1(t, f)和WVDx1x1(t, f).
Step1 将SPWVDx1x1(t, f)与WVDx1x1(t, f)点乘,得到时频模具矩阵TFMx1x1(t, f),即
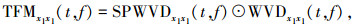
|
其中“⊙”为Hadamard积.
Step2 将TFMx1x1(t, f)进行截断处理得到自项时频地图TFAx1x1(t, f)并降噪,有
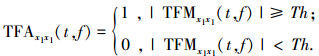
|
(11) |
式中Th为截断门限,计算公式为

|
式中:μ为门限因子, Mean{·}代表取均值.
Step3 将TFAx1x1(t, f)与SPWVDx1x1(t, f)点乘得到组合时频分布TFSYx1x1(t, f),即
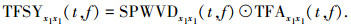
|
(12) |
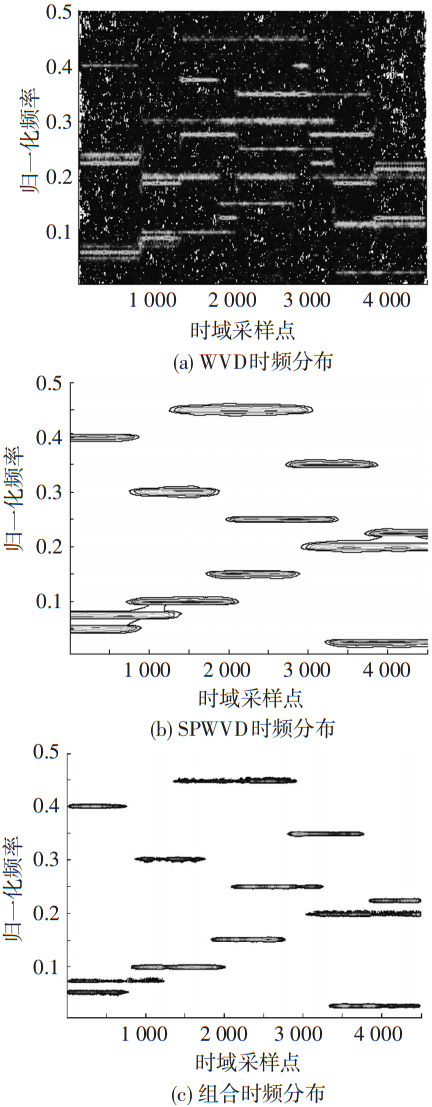
图 2为3个FH信号在信噪比5 dB时WVD、SPWVD和SPWVD&WVD结果.容易看出,SPWVD&WVD的显示效果很好,在保留WVD时频聚焦性能的同时,对交叉干扰项和噪声也进行了很好抑制.
|
图 2 FH信号在信噪比5 dB时WVD、SPWVD和SPWVD&WVD组合时频分布结果 |
由式(11)、(12)知,TFSYx1x1(t, f)中各hop的自项区为SPWVDx1x1(t, f)中对应hop的子集,因此,根据参考阵元确定的各hop自项区域提取时频点构造SPSTFT/SPTFD矩阵.对于SPTFD,时频分布采用与SPWVD性能近似计算量却大为降低的SPW分布.
3 2D-DOA与极化参数联合估计 3.1 基于SPSTFT矩阵的快速估计方法假设各FH信号不相关,根据式(6)及式(9),对信号sn第i个hop的有效时频点(ta, fa),其SPSTFT矩阵为

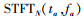
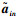
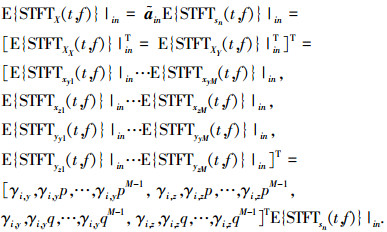
|
(13) |
式中:p=e-j2πd1cos(δi)/λin, q=e-j2πd2cos(βi)/λin(λin= c/fin,fin为载频值).
观察式(13)发现,可通过计算ULA1和ULA2同向通道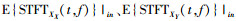
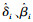

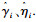

|
将
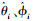
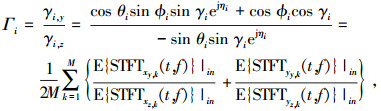
|
(14) |
由式(14)可得极化参数估计值为:
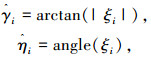
|
其中

|
由上述推导可见,该方法直接通过SPSTFT矩阵元素估计2D-DOA和极化参数,且时频分析采取可利用FFT快速实现的STFT,计算量很小.
3.2 基于SPTFD矩阵的高精度估计方法 3.2.1 信源方位和极化参数“去耦合”当某hop出现频率碰撞的多源情况时,SPSTFT矩阵的快速估计方法不再适用(当然,本方法同样适用于无频率碰撞情况).此时根据式(7)构造SPTFD矩阵E{DXX(t, f)}|in,对其进行特征值分解求得噪声子空间UN,根据子空间原理有
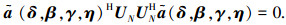
|
(15) |
考虑噪声和有限快拍数影响,通过求解以下问题估计2D-DOA和极化参数
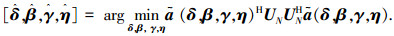
|
(16) |
式中: 
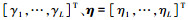
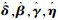
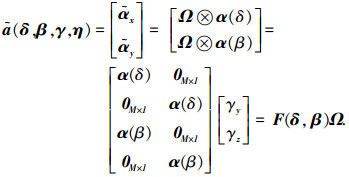
|
(17) |
式中:F(δ, β)中只包含由波程差导致的相位差;Ω中只包含极化参数.将式(17)代入式(15)得

|
(18) |
当且仅当(δ, β)为信源真实方位时,式(18)成立.由于Ω不全为0,根据秩损理论[14],可通过2维搜索得到成对的俯仰角和方位角
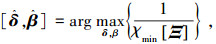
|
(19) |
其中χmin[·]表示求矩阵最小特征值运算.
3.2.2 2D-DOA估计由式(19)估计2D-DOA仍需2维搜索,以下寻找满足旋转不变关系的成对子阵,根据ESPRIT原理首先估计俯仰角,从而降低搜索维度,进一步降低运算量.重写流型矩阵为

|
设Ap1和Ap2分别为由A的第1, 3, …, 2M-1行和第2, 4, …, 2M行元素组成的子阵,即满足
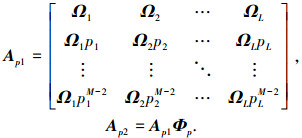
|
式中: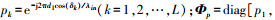
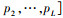
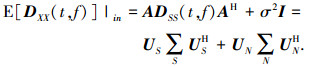
|
式中:σ2为噪声功率;
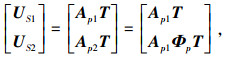
|
类似地,有
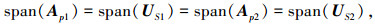
|
所以,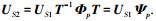
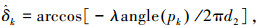
|
(20) |
其中,Ψp利用最小二乘ESPRIT算法[15]求得,即
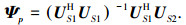
|
将式(20)得到的俯仰角估计值代入式(19),可得到方位角的计算方法为
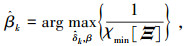
|
至此完成了2D-DOA估计,且俯仰角与方位角实现了自动配对.
3.2.3 极化参数估计对于第k个信源
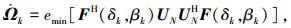
|
(21) |
其中emin[·]为求矩阵最小特征值对应的特征矢量运算.结合极化矢量表达式(1),可得极化比为
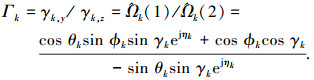
|
(22) |
因此极化参数估计值为:

|
其中

|
式中:cos θk、cos ϕk分别由式(2)求得.
上述分析可知:1)基于SPTFD矩阵的方法采用参数“去耦”结合秩损原理可在保证估计精度前提下降低搜索空间维度,显著降低算法计算量,同时实现俯仰角、方位角和极化参数间的自动配对;2)空间存在的FH信号总数可能大于侦察系统的接收天线数,但本文算法在时-频二维联合域上将FH信号分解为一个个hop,通过对各hop依次进行估计来实现所有FH信号的2D-DOA和极化参数估计,由于对各hop估计时为超定条件(发生频率碰撞的概率很小,即使发生,此hop对应的信号数目一般也小于阵元数),因此本文算法能适用于FH信号数目大于阵元数的欠定条件.
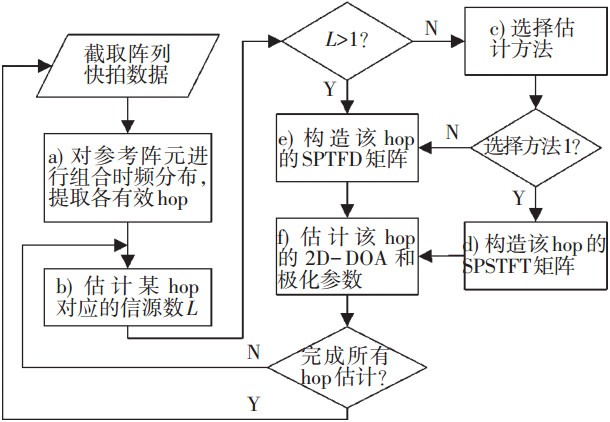
3.3 算法步骤根据以上推导和阐述,可得本文算法流程如图 3所示(基于SPSTFT矩阵的方法记为方法1,基于SPTFD矩阵的方法记为方法2).
|
图 3 算法流程 |
L型阵列的两ULA阵元间距均为1.5 m.5个远场FH信号记为FH1~FH5,跳周期均为10 us,载频在0~0.5(归一化频率)之间随机跳变,待估参数分别为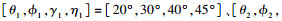
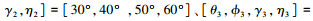
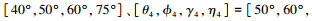
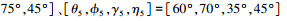

|
式中: 
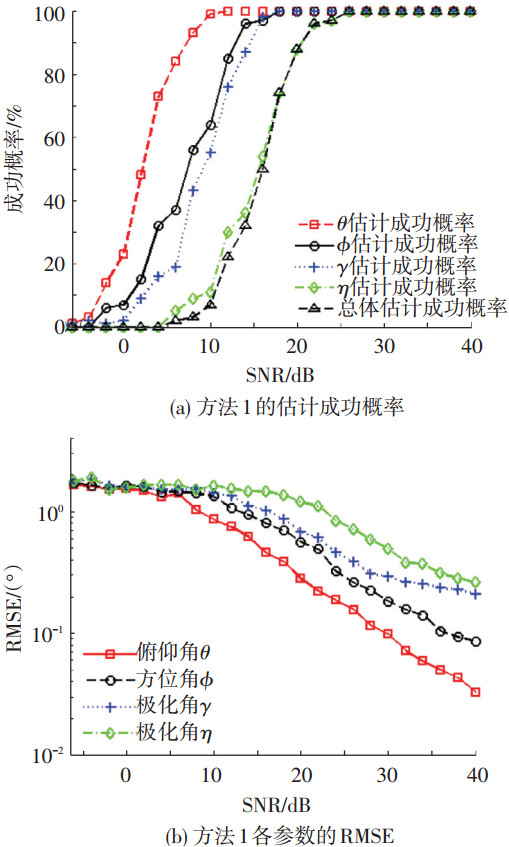
实验1 暂无频率碰撞,空间存在FH1、FH2和FH3,ULA阵元数M设为4,信噪比SNR从-6 dB以2 dB间隔递增到40 dB,各SNR下进行100次Monte-Carlo试验.分别统计入射信号θ、ϕ、γ和η的(总体)估计成功概率(成功概率定义见文献[14])及RMSE,如图 4,5所示.
|
图 4 方法1估计性能与信噪比的关系 |

|
图 5 方法2估计性能与信噪比的关系 |
图 4,5表明,随着SNR的提高,所有参数的估计成功概率均逐渐变高:SNR>20 dB时,方法1的总体估计成功概率接近100%(同一指标方法2要求SNR>10 dB);两方法性能差异主要在于方法1未充分利用阵列孔径,且不是子空间类方法,不具超分辨能力.俯仰角和方位角的估计成功概率较高,受SNR和2D-DOA估计精度的综合影响,极化参数的估计成功概率相对较低,但当SNR>8 dB时(方法2)也逐渐接近100%.两方法的RMSE均较小,方法1的RMSE值略大于方法2,且在SNR < 10 dB时下降趋势不明显.方法2俯仰角的RMSE值最小,方位角次之,极化参数略差,原因在于:俯仰角是由ESPRIT算法率先求得,估计精度主要受噪声影响;方位角是在求得俯仰角后将其回代入谱估计器,通过一维角度搜索得到,故误差还包括俯仰角估计误差;极化参数误差则受2D-DOA估计误差和噪声的综合影响.
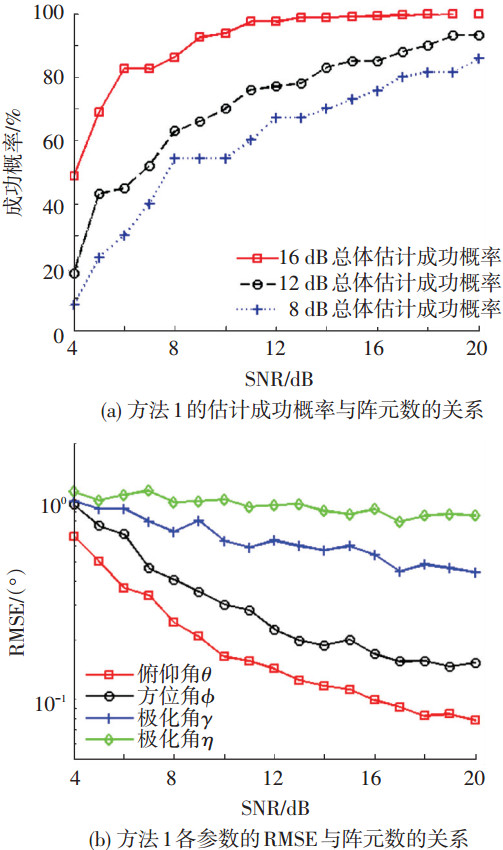
实验2 为测试阵元数目对方法1的估计性能影响,SNR分别取8、12、16 dB,ULA阵元数从4以1为步进递增至20,其余仿真条件同实验1,得到性能曲线如图 6所示.
|
图 6 方法1估计性能与阵元数的关系 |
由图 6(a)可见,阵元数对方法1的性能具有较大影响:随着阵元数增加,总体估计成功概率逐渐提高(SNR=16 dB,阵元数大于16时达到100%).图 6(b)为SNR=12 dB时各参数RMSE值与阵元数的关系曲线,结果表明,阵元增加时,各参数的RMSE值均逐步降低,相比之下,极化参数的RMSE值下降不明显.
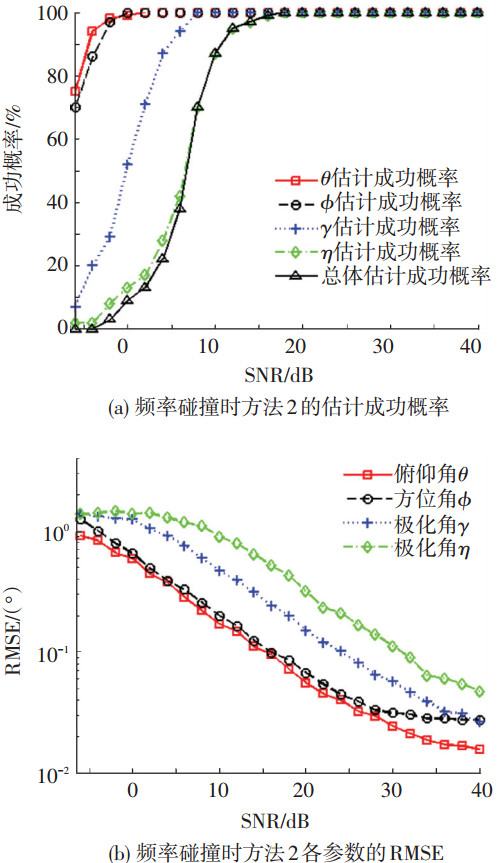
实验3 5个FH信号同时存在,设定任意两FH信号发生频率碰撞的概率为1(每次试验随机选择一个hop发生碰撞),3个信号以上碰撞概率为0,其余仿真条件与实验1相同,方法2的估计结果如图 7所示.
|
图 7 频率碰撞时方法2估计性能与信噪比的关系 |
图 7表明,当FH信号存在大概率频率碰撞时,方法2的估计性能仍然非常优良:SNR>12 dB时,总体估计成功概率接近100%;SNR>8 dB时所有参数RMSE值均小于1°.对比图 7与图 4发现,实验3估计性能略差于实验1,原因主要有:1)频率碰撞时相应hop为多源估计,性能差于无碰撞的单源情况;2) 5个信号共存一定程度上加剧了信号间互扰.本实验设定的碰撞概率条件非常苛刻,已远超实际情况,因此方法2处理频率碰撞的FH信号同样具有优异性能.
方法2(利用z轴子阵估计俯仰角,传统算法可估计的信源数小于M)基于单臂4阵元实现了5个FH信号的有效估计,验证了其在欠定条件下的估计能力.
5 结论1) 新方法利用SPWVD&WVD组合时频分布定位各跳自项,从而降低了FH交叉项对参数估计精度的影响;设计的SPTFD/SPSTFT矩阵构造方法降低了该处理环节计算量;极化和方位信息“去耦合”避免了多维参数寻优和配对.
2) 理论分析和仿真实验证明:基于SPSTFT矩阵的方法在计算量方面优势明显,是快速估计场合的备选方案;基于SPTFD矩阵的方法估计性能优于SPSTFT矩阵法,并能处理发生频率碰撞的hop,但计算量略高于SPSTFT矩阵法.
| [1] |
FU Kuoching, CHEN Yungfang. Blind iterative maximum likelihood-based frequency and transition time estimation for frequency hopping systems[J]. IET Communications, 2013, 7(9): 883-892. DOI:10.1049/iet-com.2012.0557 |
| [2] |
LIU Xiangqang, SIDIROPOULOS N D, SWAMI A. Blind high-resolution localization and tracking of multiple frequency hopped signals[J]. IEEE Transactions on Signal Processing, 2002, 50(4): 889-901. DOI:10.1109/78.992136 |
| [3] |
LIU Xiangqang, SIDIROPOULOS N D, SWAMI A. Joint hop timing and frequency estimation for collision resolution in FH networks[J]. IEEE Transations on Wireless Communications, 2005, 4(6): 3063-3074. DOI:10.1109/TWC.2005.858006 |
| [4] |
LIN C H, FANG W H. Joint angle and delay estimtion in fr equency hopping systems[J]. IEEE Transaction on Aerospace and Electronic Systems, 2013, 49(2): 1042-1056. DOI:10.1109/TAES.2013.6494398 |
| [5] |
陈利虎, 张尔扬. 基于数字信道化和空时频分析的多跳频信号DOA估计[J]. 通信学报, 2009, 30(10): 68-74. |
| [6] |
陈利虎. 基于空时频分析的多分量跳频信号DOA估计[J]. 系统工程与电子技术, 2011, 33(12): 2587-2592. DOI:10.3969/j.issn.1001-506X.2011.12.04 |
| [7] |
王永明, 王世练, 张尔扬. 多跳频脉冲的高效测向算法多跳频脉冲的高效测向算法[J]. 哈尔滨工程大学学报, 2011, 32(5): 662-666. |
| [8] |
WONG K T, LI Linshan, ZOLTOWSKI M D. Root-MUSIC-based direction finding and polarization estimation using diversely polarized possibly collocated antennas[J]. IEEE Antennas Wireless Propagation Letters, 2004, 3(1): 129-132. |
| [9] |
GARREN D A, ODOM A C, OSBORN M K, et al. Full-polarization matched-illumination for target detection and identification[J]. IEEE Transaction on Aerospace and Electronic Systems, 2002, 38(3): 824-837. DOI:10.1109/TAES.2002.1039402 |
| [10] |
WONG K T. Blind beamforming/geolocation for wideband-FFHs with unknown hop-sequences[J]. IEEE Transaction on Aerospace and Electronic Systems, 2001, 37(1): 65-76. DOI:10.1109/7.913668 |
| [11] |
ZHANG Yimin, OBEIDAT B A, AMIN M G. Spatial polarimetric time frequency distribution for direction of arrival estimation[J]. IEEE Transaction on Signal processing, 2006, 54(4): 1327-1340. DOI:10.1109/TSP.2005.863124 |
| [12] |
庄钊文, 徐振海, 肖顺平, 等. 极化敏感阵列信号处理[M]. 北京: 国防工业出版社, 2005: 199-212.
|
| [13] |
XIA Tieqi, ZHENG Yi, WAN Qun, et al. Decoupled estimation of 2-D angles of arrival using two parallel uniform linear arrays[J]. IEEE Transactions on Antennas and Propagation, 2007, 55(9): 2627-2632. DOI:10.1109/TAP.2007.904143 |
| [14] |
张东伟, 郭英, 齐子森, 等. 采用空间极化时频分布的跳频信号多参数联合估计算法[J]. 西安交通大学学报, 2015, 49(8): 17-23. DOI:10.7652/xjtuxb201508004 |
| [15] |
LEMMA A N, VAN DER VEEN A J, DEPRETTERE E F. Analysis of joint angle-frequency estimation using ESPRIT[J]. IEEE Transactions on Signal Processing, 2003, 51(5): 1264-1283. DOI:10.1109/TSP.2003.810306 |
 2016, Vol. 48
2016, Vol. 48


